Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Designing stimulus-sensitive colloidal walkers†
Francisco J.
Martinez-Veracoechea
a,
Bortolo M.
Mognetti
ab,
Stefano
Angioletti-Uberti
ac,
Patrick
Varilly
a,
Daan
Frenkel
a and
Jure
Dobnikar
*ad
aUniversity of Cambridge, The University Chemical Laboratory, Lensfield Road, CB2 1EW, Cambridge, UK. E-mail: jd489@cam.ac.uk
bCenter for Nonlinear Phenomena and Complex Systems, Université Libre de Bruxelles, Code Postal 231, Campus Plaine, B-1050 Brussels, Belgium
cDepartment of Physics, Humboldt-University Berlin, Newtonstrasse 15, 12489 Berlin, Germany
dDepartment of Theoretical Physics, Jožef Stefan Institute, Jamova 39, 1000 Ljubljana, Slovenia
First published on 11th February 2014
Abstract
Colloidal particles with DNA “legs” that can bind reversibly to receptors on a surface can be made to ‘walk’ if there is a gradient in receptor concentration. We use a combination of theory and Monte Carlo simulations to explore how controllable parameters, e.g. coating density and binding strength, affect the dynamics of such colloids. We find that competition between thermodynamic and kinetic trends imply that there is an optimal value for both the binding strength and the number of “legs” for which transport is the fastest. Using available thermodynamic data on DNA binding, we indicate how directionally reversible, temperature-controlled transport of colloidal walkers can be achieved. In particular, the present results should make it possible to design a chromatographic technique that can be used to separate colloids with different DNA functionalizations.
1 Introduction
The study of DNA-coated colloids (DNACCs) started with two seminal papers, one by the group of Mirkin1 and one by Alivisatos and collaborators.2 Since then, DNACCs have become a vibrant area of research that includes experiments1–14 and modelling.15–24 Recent reviews covering both aspects of DNACC-based materials science can be found in ref. 25 and 26. The goal of most studies to date was to induce the self-assembly of the predesigned crystalline structure of DNACCs, by tuning the DNA-mediated colloidal interactions.3,4,12,13,15 Yet, other promising areas where DNA programmability can be exploited are quickly emerging: a notable example is development of DNA-based motors27,28 that move in a programmable and reproducible way. Such motors could find applications in the step-by-step synthesis of macromolecules,29–31 or in DNA-based computing.32,33Here we investigate how DNACCs functionalized with different nucleotide sequences can be used as nano- or micro-scale transporters. We study colloids coated with DNA molecules that are mostly composed of inert double-stranded DNA (dsDNA) sequences but have a ‘sticky’ single-stranded DNA (ssDNA) end. The colloids move on surfaces coated with concentration gradients of ssDNA strands with complementary sequences. Using a combination of theory18,19 and Monte Carlo (MC) simulations, we analyse how such directional motion depends on experimentally tunable parameters, such as the number of DNA “legs” on each colloid, the hybridisation free-energy of their sticky ends, and the grafting density of the surface strands. We demonstrate that it is possible to engineer a system such that the motion can be reversed by changing temperature, pH, salt concentration, or other external parameters. Such switchability would enable novel applications like cyclable transport of specific substances on DNA tracks. Finally, we indicate how our results could be used to design a chromatographic tool to separate DNACCs with different functionalizations.
2 Modelling of DNA-based walkers
In Fig. 1 we show a typical setup for DNACCs walking on a coated surface. To model DNACCs we use a coarse-grained model23,34 that has been shown to reproduce all features of the phase behaviour of DNACCs (Fig. 1b) (for details of the model please see the Methods section). In this model, the colloids are represented as hard-spheres with radius Rc. We assume that the DNA chains are long enough to be modelled as soft “blobs”,35 whose only degree of freedom is the position of the center of mass. Blobs interact with each other through a Gaussian repulsion and with colloids or the flat surface via an exponential repulsion. To each colloid, we attach a number κ of DNA chains. A harmonic spring represents the binding of the DNA chain to the surface. These attached blobs act as “legs” that can freely move along the surface of the colloids.34 The surface z = 0 is grafted with immobile DNA blobs that are distributed in a random way along the y axis and with a linear grafting density gradient along the x axis. In all cases discussed below, we average all observations over multiple realisations of the surface grafting points. | ||
| Fig. 1 Nanocolloids walking on a DNA-coated surface. Atomistic detail (left) and coarse-grained representation (right). | ||
DNAs on the colloids have a single-stranded sticky end that is complementary to the sticky ends on the surface. A given pair of complementary DNAs is either bound or unbound. If two DNA blobs are bound, the free energy of the system shifts by an amount βf (β = 1/kBT, where kB is Boltzmann's constant and T the temperature), and the centers of mass of the bound blobs interact via an additional harmonic spring potential.34 The binding energy βf is related by a constant shift to the hybridisation free energy of the sticky ends in solution under standard conditions, for colloids with a diameter 100 nm, we have f ≈ ΔG0 + 11.6 kBT (see Materials and methods section for more detail), where ΔG0 is the hybridisation free energy of complementary single-stranded sticky ends forming a bond.
On a surface with a receptor gradient, the DNACCs are subject to an effective force in the direction of the gradient. The interaction free-energy between the colloid and the substrate is determined by a combination of the hybridisation free energies of the single bonds and by the combinatorial entropy due to the formation of multiple bonds between the particles and the surface. The free energy profile can be evaluated using a recently developed self-consistent mean-field theory.18,19
The mean-field theory (described in detail in the Methods section) disregards DNA–DNA excluded volume interactions and is therefore approximate (but qualitatively correct) for nano-sized colloids that typically have relatively high coating densities. For micron-sized colloids, which display lower functionalization densities, the neglected interactions are almost negligible, hence the theory approaches quantitative accuracy18,19 and can be used as a powerful tool to explore the mechanisms of colloidal motility.
The calculated free energy profiles (see Fig. 4 in the Methods section) feature two regimes characterized by the dominance of either the enthalpy of hybridisation or the combinatorial entropy. As expected, the DNACCs generally experience a strong driving force to “walk” up the concentration gradient. This thermodynamic driving force monotonically increases as the number of DNAs per colloid κ and the binding strength (βf more negative) are increased.
However, the free-energy gradients do not completely determine the efficiency of colloidal transport on the surfaces: if the hybridisation free energy βf becomes too negative, the kinetics of unbinding slows down. Similarly, when the number of “legs” κ is increased, it becomes more difficult for the colloid to move as it is anchored in multiple places. To explore the competition between the opposing thermodynamic and kinetic effects we performed kinetic MC simulations where we initially put the colloids at x = 0 and let them diffuse freely. Details of the kinetic Monte Carlo moves are described in the Materials and methods section. For the trial moves that account for bond-forming/bond-breaking we followed the procedure described in ref. 34. We kept track of the position of the colloid at different simulation times. Since we are interested in the regime where the motion of the colloid is entirely due to DNA hybridization, we impose the restriction that the translation moves of the colloid are only attempted if at least one of its DNA chains is hybridized.
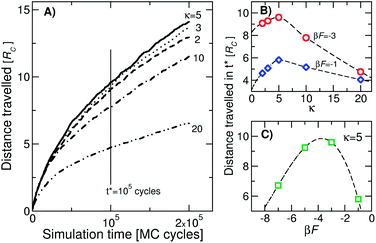
In Fig. 2(A) we show the average of the distance travelled by colloids with different values of κ at βf = −3. The averaging was based on 2000 trajectories. On average, the colloids move in the direction of increasing concentration of surface DNA as time progresses. The kinetics of the system is governed by the rate of hybridisation and breaking of the single bonds. In ref. 36 the lifetime of a single bond has been shown to be of the order of μs. Since we typically attempt about 10 to 100 binding/unbinding events in a single MC cycle, the corresponding real timescale can be estimated. A rough estimate predicts that the walking speeds can be up to microns per second, which is comparable to the speed of biological molecular motors. Of course, the actual speed depends on the design parameters of the system. Our kinetic simulations reveal (Fig. 2(B) and (C)) that an optimum value of βf and κ exist where colloids walk the fastest in the direction of the concentration gradient: kopt ≈ 5 and βFopt ≈ −4. While these exact values should depend to some extent on the model and simulation details, the existence of an optimal parameter set (kopt, βFopt) is due to the competition between kinetics and thermodynamics, and is thus a general feature of the system.
The observed behaviour suggests a chromatographic method to separate DNACCs with different functionalizations. In a traditional chromatographic column each reaction product moves over a different distance owing to a different interaction with the substrate, and the same happens for DNACCs that differ in the number of DNA “legs”. Especially for the case of nano-sized colloids where the average number of strands shows greater relative variation due to their small size, obtaining uniformly functionalized colloids is important for applications. For instance, statistical fluctuations of the number of grafted DNA may interfere with the formation of ordered crystals. We suggest a simple method to characterize the colloids: on a coated surface with a gradient in receptor concentration the colloids coated with complementary sticky ends will move along the gradient. At a given temperature, their speed will depend on the functionalization κ and after a finite time they will be spatially separated. Since, due to the non-monotonic behavior of walking efficiency (Fig. 2), the separation will not be complete, we could repeat the process at a different temperature in order to further differentiate the colloids. Our results allow us to design – according to the experimental details of the system – an optimal temperature cycle for efficient separation.
3 Designing reversible DNACC walkers
In the system described above, the colloidal motion can be controlled by external parameters, e.g. temperature, salt concentration or pH. As a proof of principle, we show here how to design DNACC walkers with the ability to reverse their direction of motion as a function of temperature. The approach that we propose is based on the possibility to swap between two kinds of linkages (see Fig. 3). This is encoded in the hybridisation free energies of the two competing linkages (ΔGα and ΔGβ) that are designed to invert their relative strength as the temperature is lowered. In order to engineer this changeover behaviour, it is useful to decompose the hybridisation free energy into the configurational term (ΔGc) and the sticky-ends term (ΔGx0)| ΔGx = ΔGc + ΔGx0, x = α, β. | (1) |
 | ||
| Fig. 3 Sticky-end architecture. The sticky ends on the colloidal “legs” are designed so that they can bind to two different receptors α and β. The relative binding strength and thus the direction of motion can be regulated by temperature as shown in the plot of the binding free energy as a function of the temperature. The calculations were made for the strands in eqn (4); the data shown are for sticky ends Sγ binding to the substrate receptors Sα (solid lines) and Sβ (dashed lines). Results are plotted for two different salt concentrations: 0.06 M (black) and 1 M (red). The sequences have been designed so that there is a transition temperature Tc, at which the preferable binding changes from α (T < Tc) to β at T > Tc. | ||
ΔGx0 depends on the sticky-end sequences and is highly sensitive to the temperature, whereas ΔGc is an entropic term depending on the accessible configurations for the tethering part of DNA (i.e., that which is not involved in the hybridisation into dsDNA when bonds are formed). To a first approximation, ΔGc, when measured in units of the thermal energy kBT, is independent of temperature. In principle one could use different tethering parts to control the binding free energy. However, this requires detailed calculation of ΔGc, which requires a detailed model of the tethering polymers and its interactions. Such a model may not always be available. For design purposes it is therefore better to consider a system of colloids for which all sticky ends are tethered to the colloidal surface by the same type of polymer. This implies that the tether has no effect on the relative strength of different bonds and that the only parameter we need to tune is ΔGx0, the hybridisation free energy of the bonding pairs. We recall that ΔGx0 is the sum of enthalpic and entropic contributions
| ΔG0 = ΔH0 − TΔS0, | (2) |
In view of the above, we have constructed the sequences s as a series of non-reactive poly-T strands (Tn) that connect the tethering points with the reactive sticky ends S:
| sx = 5′ − (Tn)Sx − 3′, | (3) |
In order to design appropriate sticky ends Sx, we considered the case where the sticky end of the colloidal “leg” Sγ consists of two nucleotide sequences, Sγ = ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) α +
α + ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) β, and can bind to two complementary receptor sequences Sα and Sβ (see Fig. 3). We chose the Sα complementary part to be shorter than Sβ but with a larger number of “strong” G–C bonds, as opposed to “weak” A–T bonds.37 For such sequences, we expect the following behavior: at high temperatures, where the entropic term in eqn (2) dominates, the shorter Sγ–Sα pair will have a lower hybridisation free energy: ΔGα < ΔGβ. As temperature decreases, the entropic penalty becomes less relevant with respect to the enthalpic gain, and the free energy ΔGβ of the longer Sγ–Sβ pair that is capable of forming more bonds will be lower. Since γ can bind either to α or to β but not likely to both,§ a crossover in binding affinity is expected at a temperature TC. By varying the length of the sequences and the relative number of strong G–C bonds, the relative hybridisation free energy of the two sequences and the crossover temperature TC can be controlled. We have used the DINAMelt web server38 to evaluate the hybridisation free energy (eqn (2)) and designed the sticky-end sequences in such a way as to observe the crossover at temperature between 30 °C < TC < 50 °C. Two sticky-end sequence sets Sx that we designed in this way are:
β, and can bind to two complementary receptor sequences Sα and Sβ (see Fig. 3). We chose the Sα complementary part to be shorter than Sβ but with a larger number of “strong” G–C bonds, as opposed to “weak” A–T bonds.37 For such sequences, we expect the following behavior: at high temperatures, where the entropic term in eqn (2) dominates, the shorter Sγ–Sα pair will have a lower hybridisation free energy: ΔGα < ΔGβ. As temperature decreases, the entropic penalty becomes less relevant with respect to the enthalpic gain, and the free energy ΔGβ of the longer Sγ–Sβ pair that is capable of forming more bonds will be lower. Since γ can bind either to α or to β but not likely to both,§ a crossover in binding affinity is expected at a temperature TC. By varying the length of the sequences and the relative number of strong G–C bonds, the relative hybridisation free energy of the two sequences and the crossover temperature TC can be controlled. We have used the DINAMelt web server38 to evaluate the hybridisation free energy (eqn (2)) and designed the sticky-end sequences in such a way as to observe the crossover at temperature between 30 °C < TC < 50 °C. Two sticky-end sequence sets Sx that we designed in this way are:
 | (4) |
 | (5) |
The dependence of the hybridisation free energy ΔG0 for one of the above solutions (eqn (4)) on temperature is shown in Fig. 3. We see that the binding free energy indeed has a crossover temperature, at which the relative binding strength of the colloidal legs to receptors α and β changes sign. The red and black sets of curves illustrate the dependence of the crossover temperature on salt concentration.
Using our ability to switch the relative strength of α and β bonds, we can now design a system where the direction of the walkers' motion can be changed with temperature. We assume that the surface has been prepared such that its overall grafting density σ is uniform, however, the densities of the two strands σα and σβ have gradients in opposite directions, e.g. σα = σ(1 − x/L) and σβ = σx/L. On such a surface, the colloidal walker will follow the direction that maximizes the number of strong bonds, since the combinatorial entropy due to the different possible configurations of bonds remains constant throughout the system. However, the relative strength of the bonds depends on temperature and hence, changing the temperature one can reversibly change the direction of walking. It is possible to design similar systems with the pH or salt concentration – instead of the temperature – as the control parameter. We note that many examples of unidirectional motion of colloids along surface gradients have been reported in the literature.27,28,39 However, to the best of our knowledge, the technique that we propose to control the direction of motion of the colloids is new.
The driving force moving the reversible walkers is the replacement of weak bonds with stronger ones (this regime has been defined ‘enthalpic’ in Section 5.3). For this reason, directed motion (in contrast to random diffusion) can be achieved also when all strands on the colloids are hybridised. In this respect the reversible walkers are analogous to a vitrimer system, for which any rearrangement is achieved without varying the degree of cross-linking between polymers.40 In vitrimers, swapping between different bonding configurations can be achieved only in the presence of an appropriate catalyst and at sufficiently high temperatures. These requirements stem from the necessity to effectively break strong covalent bonds before reforming them with different partners. Although DNA-hybridisation for the typical sequences we describe has a much lower energy than any covalent bond, the binding strength can still be considerable, especially at low temperatures, thus the single-bond breaking kinetics can be very slow. Under such conditions, the mobility of the colloid (i.e. the proportionality constant between its speed and the free-energy gradient) is dominated by this single-bond breaking process.20 In the field of DNA-nanotechnology some strategies have been devised to alleviate this problem, e.g. toe-holding mediated strands displacement.41 However, a detailed discussion of how these schemes could be used in our system goes beyond the scope of the present work.
The ability to reverse the direction of colloidal motion could be interesting for a variety of applications. Moreover, it would allow us to refine the chromatographic method proposed above: if we coat the surface with two kinds of receptors α and β with the binding free energies featuring a crossover as in Fig. 3 and if the two strands have density gradients in orthogonal directions, the direction of colloidal motion will depend on the temperature. By, e.g. gradually changing the temperature around the crossover temperature, we can drive the colloids along the curved trajectories, as well as separate them according to their functionalization. Finally, one could envisage separating colloids with similar sequences differing in only one or two nucleotides.
4 Methods
4.1 Modeling polymers and bond formation
We use a previously developed coarse-grained model23,34 to represent DNACCs (Fig. 1b). We model colloids as hard-spheres of radius Rc and the surface that they walk on as a hard half-space z < 0. The bare colloid–colloid interaction VHS (d), is given by | (6) |
The long, flexible dsDNA chains (gyration radius Rg = Rc/3) are modelled as soft “blobs”,35 whose only degree of freedom is the position of the center of mass. Blobs interact with each other through a Gaussian repulsion, given by
| βVbb(r) = 1.75e−0.80(r/Rg)2, | (7) |
| βVbc(z) = 3.20e−4.17(z/Rg−0.50), | (8) |
 | (9) |
The colloids move on a DNA-coated surface, with each grafted DNA represented as a blob grafted at a specific point r0 on the surface. The grafting is modelled using a harmonic spring potential, given by
 | (10) |
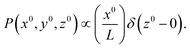 | (11) |
Here, σ is the grafting number density per unit area, and 0 ≤ x0, y0 < L. With this distribution of grafting points, there is a roughly linear grafting density gradient along the x axis. In all cases discussed below, we average all observations over multiple realisations of the surface grafting points.
DNAs on the colloids have a sticky end that is complementary to an analogous sticky end on DNA on the surface. We model this binding as a binary event: a given pair of complementary DNAs is either bound or unbound. If bound, the energy of the system shifts by an amount βf, and the centers of mass of the blobs corresponding to the DNAs interact via a harmonic spring potential. Hence, each bond adds to the potential energy of the system a term given by
| βVbond(r) = βf + 0.534(r/Rg − 0.730)2, | (12) |
| βf = βΔG0 + ln[ρ0Rg3qAB], | (13) |
4.2 Explicit simulations
In summary, the final Hamiltonian for a system with colloids centered at {Ra} and DNAs represented as blobs with centers of mass at {ri} is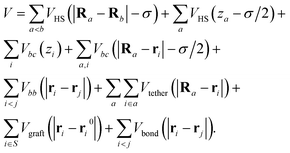 | (14) |
In this expression, i ∈ α denotes the set of DNAs i tethered to colloid a, i ∈ S denotes the set of DNAs i grafted on the surface at points {ri0}, and the primed sum is over all bound pairs of DNA chains, i and j. Respectively, the terms in the Hamiltonian capture the hard-sphere interaction between colloids, between colloids and the surface, the repulsion between DNAs and the surface, the repulsion between DNAs and colloids, the Gaussian repulsion between DNAs, the tethering of DNAs to particular colloids, the grafting of DNAs on the surface, and the binding energy between bound complementary DNAs.
Dynamics of this model is approximated by kinetic Monte Carlo simulations. Particle displacements with uniformly distributed step sizes are attempted at a frequency consistent with the free colloid having diffusion constant D = kBT/6πηRc, where η ≈ 1 cP is the viscosity of water. These moves define the correspondence between Monte Carlo steps and real time. Further, DNA blob displacements are attempted at the same frequency. Finally, hybridization is implemented via bond-forming/bond-breaking MC moves as described in ref. 34, with a frequency chosen to mimic realistic DNA hybridisation kinetics. Such a model can realistically capture the stochastic nature of binding events, which dominates the dynamics of nanocolloids with relatively few “legs”.
4.3 Implicit modelling of micron-size colloids: a mean field approach
For micron-sized DNACCs, a common grafting setup uses short dsDNA tethers (modeled as rigid rods) capped with short sticky ends.6,9,11 We have used our previously developed self-consistent mean field theory18,19 to map the free energy landscape experienced by such colloids. For concreteness, we have chosen to model tethers that are 20 nm long. The colloid is taken to have a radius R = 0.5 μm and be coated with strands of type γ, randomly and uniformly, at a density, σ, equal to 1 tether per 5 nm. The surface is coated with a gradient of α and β-type strands (please refer to Fig. 3 for details). At one end, the density of α-type strands is 2σ, and there are no β strands. The converse situation holds at the opposite end of the gradient. The parameter c measures progress along this linear gradient. The solution binding free energy of α and γ sticky ends is given by ΔG0 − δ/2, while that of β and γ strands is given by ΔG0 + δ/2. No other pairs of sticky ends have appreciable binding.To compute the colloid-surface interaction free energy at any point c on the surface, we first compute the interaction free energy per unit area, f(h′), of two plates with coats and grafting densities corresponding to the value of c, as a function of plate–plate separation, h′. We then use the Derjaguin approximation to estimate the interaction between a spherical colloid and the planar surface, F(h), as a function of the distance of the closest approach, h, i.e.
Since F(h) varies strongly with h, we assume that the particle sits at or very close to the height h that minimizes F(h), which is usually equal to the tether length, i.e. 20 nm. The value of F at that height is used to estimate the free energy of binding. As long as the curvature of F(h) around this minimum is independent of c, this estimate differs from the real binding free energy by a constant amount, which does not affect the particle's surface dynamics.
Fig. 4 shows the free energy of binding as a function of the progress, c, along the surface coating gradient, for δ = 8 kBT, as a function of mean sticky-end binding strength, ΔG0. At high overall binding strengths (ΔG0 around −12 kBT), there are two clearly visible regimes in this free energy landscape. For c < 0.5, it is impossible for all the γ-type strands in the colloid to bind to the more favorable surface α-type strands as opposed to β-type strands. Hence, moving the particle along the surface-coating gradient results in a decrease in free energy owing to more favorable binding partners being available to the colloid's tethers. Essentially all γ-type strands on the colloid are bound, and the decrease in free energy is linear along the gradient, with a slope proportional to δ. We call this regime the enthalpic regime. For c > 0.5, all γ strands can and do bind to α strands on the surface. Hence, the gradient in free energy is driven purely by the increase in the number of α partners available to the colloid. We call this regime the entropic regime.
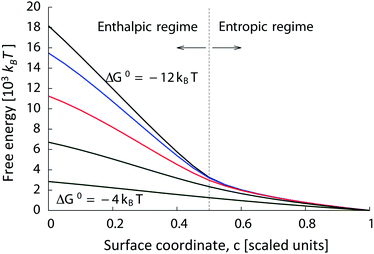 | ||
| Fig. 4 Relative binding free energy of micron-sized DNACC to the surface along a linear surface coating gradient. The colloid is coated with γ-type strands with a density σ = 1/(5 nm).2 Along the surface, the density of α-type strands is 2σ(1 − c) and that of β-type strands is 2σc. The binding free energy of sticky ends α and γ in solution is ΔG0 − 4 kBT, and that of β and γ strands is ΔG0 + 4 kBT. Free energy landscapes are shown for −ΔG0 = 12, 10, 8, 6 and 4 kBT. The last curve with ΔG0 = −4 kBT corresponds to ΔGα = 0 and ΔGβ = −8 kBT, which is roughly equivalent to the system with only one type of receptors. | ||
At low binding strength (i.e., high ΔG0), entropic effects play an important role even at c < 0.5. There, many γ strands remain unpaired, so that α–γ bonds are not saturated at c = 0.5. Indeed, for low enough binding strengths (ΔG0 larger than about 4 kBT), the free energy decreases linearly with constant slope from one end of the surface coating gradient to the other end. Decreasing the surface grafting density by an order of magnitude reduces all binding free energies by about the same amount, without significantly changing the qualitative features of Fig. 4. A rough estimate of whether this gradient is experimentally realizable can be obtained by supposing that the particle will only move appreciably if the free energy for moving by one tether length (20 nm) is 1 kBT. Under these conditions, the linear gradient in Fig. 4 would have to be no longer than about 100 μm in size to realize both the enthalpic and entropic regimes, or no longer than about 500 μm to realize only the enthalpic regime. These sizes should be within the range of current micro-patterning techniques like dip-pen nanolithography. The mean field approach presented in this section has thus proven to be a useful tool for exploring the rich phase space of the system as well as to predict novel behaviour.
5 Conclusions
We have presented a model study of the diffusion and directed motion of DNA-coated colloids on DNA-functionalized surfaces. For the case of DNACCs coated with a small number of DNA legs, we observed a non-monotonic dependence of the diffusion rate on the number of “legs” and on their hybridization free energy. As a general consequence of the competing kinetic and thermodynamic trends, optimal parameter values exist, such that the colloids move the fastest along the receptor concentration gradients.For the case of DNACCs densely coated with DNA, we found instead two different diffusion regimes depending on the single-bond binding energy, and we identify the causes in the enthalpic-vs.-entropic nature of binding in the two different cases. Finally, we have shown how insights into the thermodynamics of DNA and DNACC interactions provide a valuable way to design possible applications for this system, and we discuss the explicit case of reversible DNACC walkers as well as the use of DNA-grafted surfaces as a chromatographic tool to separate DNACCs with different functionalizations, a process that could improve their use in a number of important technological applications. The underlying mechanisms of the phenomena that we describe are not specific to particles coated with DNA. Any colloidal system with multivalent ligand–receptor interactions should exhibit similar behaviour.
Thus the approach that we describe above could be used to separate multivalent nanoparticles according to their valence. Again, such separations would be potentially very useful for the purification of multivalent “magic bullets” for targeting specific pathogens.42
Acknowledgements
This work was supported by the 7th Framework Programme of European Union through grants ARG-ERC-COLSTRUCTION 227758, EPSRC Programme Grant EP/I001352/1 and ITN-COMPLOIDS 234810, and by the Slovenian research agency through Grant P1-0055. P.V. acknowledges funding from a Marie Curie International Incoming Fellowship of the European Community FP7 and S.A-U from an Alexander von Humboldt Postdoctoral fellowship.References
- C. A. Mirkin, R. C. Letsinger, R. C. Mucic and J. J. A. Storhoff, DNA-based method for rationally assembling nanoparticles into macroscopic materials, Nature, 1996, 382, 607–609 CrossRef CAS PubMed.
- A. P. Alivisatos, K. P. Johnsson, X. Peng, T. E. Wilson, C. J. Loweth, M. P. Bruchez and P. G. Schultz, Organization of ‘nanocrystal molecules’ using DNA, Nature, 1996, 382, 609–611 CrossRef CAS PubMed.
- S. Y. Park, A. K. R. Lytton-Jean, B. Lee, S. Weigand, G. C. Schatz and C. A. Mirkin, DNA-programmable nanoparticle crystallization, Nat. Mater., 2008, 451, 553–556 CrossRef CAS PubMed.
- D. Nykypanchuk, M. M. Maye, D. van der Lelie and O. Gang, DNA-guided crystallization of colloidal nanoparticles, Nat. Mater., 2008, 451, 549–552 CrossRef CAS PubMed.
- P. L. Biancaniello, A. J. Kim and J. C. Crocker, Colloidal Interactions and Self-Assembly Using DNA Hybridization, Phys. Rev. Lett., 2005, 94, 058302 CrossRef.
- R. W. Benjamin and J. C. Crocker, Direct measurements of DNA-mediated colloidal interactions and their quantitative modeling, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15687–15692 CrossRef PubMed.
- K. Suzuki, K. Hosokawa and M. Maeda, Controlling the Number and Positions of Oligonucleotides on Gold Nanoparticle Surfaces, J. Am. Chem. Soc., 2009, 131, 7518–7519 CrossRef CAS PubMed.
- M. E. Leunissen, R. Dreyfus, F. C. Cheong, D. G. Grier, R. Sha, N. C. Seeman and P. M. Chaikin, Switchable self-protected attractions in DNA-functionalized colloids, Nat. Mater., 2009, 8, 590–595 CrossRef CAS PubMed.
- M. E. Leunissen, R. Dreyfus, R. Sha, N. C. Seeman and P. M. Chaikin, Quantitative Study of the Association Thermodynamics and Kinetics of DNA-Coated Particles for Different Functionalization Schemes, J. Am. Chem. Soc., 2010, 132, 1903–1913 CrossRef CAS PubMed.
- R. Dreyfus, M. E. Leunissen, R. Sha, A. Tkachenko, N. C. Seeman, D. J. Pine and P. M. Chaikin, Aggregation-disaggregation transition of DNA-coated colloids: Experiments and theory, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 41404 CrossRef.
- F. Varrato, L. Di Michele, M. Belushkin, N. Dorsaz, S. H. Nathan, E. Eiser and G. Foffi, Arrested demixing opens route to bigels, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19155–19160 CrossRef CAS PubMed.
- R. J. Macfarlane, M. R. Jones, B. Lee, E. Auyeung and C. A. Mirkin, Topotactic Interconversion of Nanoparticle Superlattices, Science, 2013, 341, 1222–1225 CrossRef CAS PubMed.
- Y. Zhang, F. Lu, K. G. Yager, D. van der Lelie and O. Gang, A general strategy for the DNA-mediated self-assembly of functional nanoparticles into heterogeneous systems, Nat. Nanotechnol., 2013, 8, 865–872 CrossRef CAS PubMed.
- L. Di Michele, F. Varrato, J. Kotar, S. H. Nathan, G. Foffi and E. Eiser, Multistep kinetic self-assembly of DNA-coated colloids, Nat. Commun., 2013, 4, 2007 Search PubMed.
- S. Angioletti-Uberti, B. M. Mognetti and D. Frenkel, Reentrant melting as a design principle for DNA-coated colloids, Nat. Mater., 2012, 11, 518–522 CrossRef CAS PubMed.
- A. V. Tkachenko, Morphological Diversity of DNA-Colloidal Self-Assembly, Phys. Rev. Lett., 2002, 89, 148303 CrossRef.
- B. M. Mognetti, P. Varilly, S. Angioletti-Uberti, F. J. Martinez-Veracoechea, J. Dobnikar, M. E. Leunissen and D. Frenkel, Predicting DNA-mediated colloidal pair interactions, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E378 CrossRef CAS PubMed , online edition only.
- P. Varilly, S. Angioletti-Uberti, B. M. Mognetti and D. Frenkel, A general theory for DNA-mediated and other valence limited interactions, J. Chem. Phys., 2012, 137, 094108–094123 CrossRef PubMed.
- S. Angioletti-Uberti, P. Varilly, B. M. Mognetti, A. V. Tkachenko and D. Frenkel, Communication: a simple analytical formula for the free-energy of ligand–receptor mediated interactions, J. Chem. Phys., 2013, 138, 21102–21106 CrossRef PubMed.
- B. M. Mognetti, M. E. Leunissen and D. Frenkel, Controlling the temperature sensitivity of DNA-mediated colloidal interactions through competing linkages, Soft Matter, 2012, 8, 2213 RSC.
- T. I. N. G. Li, R. Sknepnek, R. J. Macfarlane, C. A. Mirkin and M. Olvera de la Cruz, Modeling the Crystallization of Spherical Nucleic Acid Nanoparticle Conjugates with Molecular Dynamics Simulations, Nano Lett., 2012, 12, 2509–2514 CrossRef CAS PubMed.
- C. Knorowski, S. Burleigh and A. Travesset, Dynamics and Statics of DNA-Programmable Nanoparticle Self-Assembly and Crystallization, Phys. Rev. Lett., 2011, 106, 215501 CrossRef CAS.
- F. J. Martinez-Veracoechea, B. M. Mladek, A. V. Tkachenko and D. Frenkel, Design Rule for Colloidal Crystals of DNA-Functionalized Particles, Phys. Rev. Lett., 2011, 107, 045902 CrossRef.
- B. M. Mladek, J. Fornleitner, F. J. Martinez-Veracoechea, D. Alexandre and D. Frenkel, Quantitative Prediction of the Phase Diagram of DNA-Functionalized Nanosized Colloids, Phys. Rev. Lett., 2012, 108, 268301–268305 CrossRef.
- L. Di Michele and E. Eiser, Developments in understanding and controlling self assembly of DNA-functionalized colloids, Phys. Chem. Chem. Phys., 2013, 15, 3115–3129 RSC.
- C. Knorowski and A. Travesset, Materials design by DNA programmed self-assembly, Curr. Opin. Solid State Mater. Sci., 2011, 15, 262–270 CrossRef CAS PubMed.
- B. Yurke, et al. A DNA-fuelled molecular machine made of DNA, Nature, 2000, 406, 605–608 CrossRef CAS PubMed.
- W. B. Sherman and N. C. Seeman, A Precisely Controlled DNA Biped Walking Device, Nano Lett., 2004, 4, 1203–1207 CrossRef CAS.
- M. L. McKee, P. J. Milnes, J. Bath, E. Stulz, R. K. O'Reilly and A. J. Turberfield, Programmable One-Pot Multistep Organic Synthesis Using DNA Junctions, J. Am. Chem. Soc., 2012, 134, 1446–1449 CrossRef CAS PubMed.
- H. Gu, J. Chao, S. J. Xiao and N. C. Seeman, A Proximity-Based Programmable DNA Nanoscale Assembly Line, Nature, 2010, 465, 202–205 CrossRef CAS PubMed.
- Y. He and D. R. Liu, Autonomous multistep organic synthesis in a single isothermal solution mediated by a DNA walker, Nat. Nanotechnol., 2010, 5, 778782 CrossRef PubMed.
- M. N. Stojanovic, T. E. Mitchell and D. Stefanovic, Deoxyribozyme-Based Logic Gates, J. Am. Chem. Soc., 2002, 124, 3555–3561 CrossRef CAS PubMed.
- L. Qian and E. Winfree, Scaling Up Digital Circuit Computation with DNA Strand Displacement Cascades, Science, 2011, 332, 1196–1201 CrossRef CAS PubMed.
- F. J. Martinez-Veracoechea, B. Bozorgui and D. Frenkel, Anomalous phase behavior of liquid–vapor phase transition in binary mixtures of DNA-coated particles, Soft Matter, 2010, 6, 6136–6145 RSC.
- C. Pierleoni, B. Capone and J. P. Hansen, A soft effective segment representation of semidilute polymer solutions, J. Chem. Phys., 2007, 127, 171102 CrossRef PubMed.
- W. B. Rogers, T. Sinno and J. C. Crocker, Kinetics and non-exponential binding of DNA-coated colloids, Soft Matter, 2013, 9, 6412–6417 RSC.
- J. SantaLucia, A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 1460–1465 CrossRef CAS.
- N. R. Markham and M. Zuker, DINAMelt web server for nucleic acid melting prediction, Nucleic Acids Res., 2005, 33, W577–W581 CrossRef CAS PubMed.
- N. A. Licata and A. V. Tkachenko, Colloids with key–lock interactions: Nonexponential relaxation, aging, and anomalous diffusion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 041405 CrossRef.
- D. Montarnal, M. Capelot, F. Tournilhac and L. Leibler, Silica-Like Malleable Materials from Permanent Organic Networks, Science, 2011, 334, 965–968 CrossRef CAS PubMed.
- D. Y. Zhang and E. Winfree, Control of DNA strand displacement kinetics using toehold exchange, J. Am. Chem. Soc., 2009, 131, 17303–17314 CrossRef CAS PubMed.
- F. J. Martinez-Veracoechea and D. Frenkel, Designing super selectivity in multivalent nano-particle binding, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10963–10968 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3sm53096e |
| ‡ Note that the length of the (Tn) sequences contributes to the configurational part of the hybridisation free energy, ΔGc, which – as argued above – does not depend on temperature. |
| § When tethered to a substrate, simultaneous binding of the same DNA filament to two other strands would require a high entropic penalty ΔGc and thus cannot occur. This is not true for free strands in solution, a difference that is exploited in the design of DNA-origami. |
| This journal is © The Royal Society of Chemistry 2014 |