 Open Access Article
Open Access ArticleHydrodynamic interactions induce anomalous diffusion under partial confinement†
J.
Bleibel
*ae,
A.
Domínguez
b,
F.
Günther
c,
J.
Harting
cd and
M.
Oettel
e
aMax-Planck-Institut für Intelligente Systeme, Heisenbergstr. 3, 70569 Stuttgart, Germany. E-mail: bleibel@is.mpg.de
bFísica Teórica, Universidad de Sevilla, Apdo. 1065, 41080 Sevilla, Spain. E-mail: dominguez@us.es
cFakulteit Technische Natuurkunde, Technische Universiteit Eindhoven, Den Dolech 2, 5600MB Eindhoven, The Netherlands
dInstitut für Computerphysik, Universität Stuttgart, Allmandring 3, 70569 Stuttgart, Germany
eInstitut für Angewandte Physik, Universität Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany
First published on 17th February 2014
Abstract
Under partial confinement, the motion of colloidal particles is restricted to a plane or a line but their dynamics is influenced by hydrodynamic interactions mediated by the unconfined, three-dimensional flow of the embedding fluid. We demonstrate that this dimensionality mismatch induces a characteristic divergence in the collective diffusion coefficient of the colloidal subsystem. This result, independent of the specific interparticle forces in the colloid, is solely due to the kinematical constraint on the colloidal particles, and it is different from the known divergence of transport coefficients in purely one or two-dimensional fluids.
The diffusive behavior of macroobjects in solution (colloids, micelles, polymers…) is of major importance for addressing fundamental aspects of Statistical Physics and for applications. Diffusion governs the transport of particles in heterogeneous environments often encountered in soft matter and biological systems; therefore normal and anomalous diffusion have been studied by the corresponding communities from different viewpoints and with diverse methods.1–6 A fundamental characterization of the diffusive dynamics is provided by diffusion coefficients. For the simplest case of a dispersion of colloidal particles, the Fourier components δρk(t) of the particle number density field evolve according to
 | (1) |
The dynamics of colloidal solutions in confinement or near physical boundaries has also been of long-standing interest. The effect of HI has been investigated theoretically on systems confined between walls,7–9 close to a free interface,10,11 or on solutions with a matrix of fixed obstacles.12 Trapped objects in (fluid) membranes also show peculiar diffusion behavior.13,14 In this communication, we investigate the generic case of partial confinement: one part of the system, namely the colloidal particles, is restricted to move in one or two dimensions, whereas the other part, namely the embedding solvent, evolves in a (essentially unbound) three-dimensional (3D) domain. Examples of experimental realizations of such a partial confinement setup are numerous, e.g., a colloidal monolayer at a fluid interface,15 or particles restricted by optical tweezers to stay in a plane or a line.16 Here we study this problem both theoretically with a simplified model and numerically with simulations of a more complete model. The main result is that the HI induce anomalous fast diffusion.
Theory
We present the fundamental idea (further elaborated in the ESI†) with a theoretical model for the long-time, collective diffusion specific to particles confined to a planar monolayer. We use the convention that z-components of any 3D position vector are set to zero (location of the plane), r = (x,y,0). The areal number density ρ(r,t) of particles at the plane and the particle velocity field v(r,t) = (vx,vy,vz = 0) are related by the continuity equation, | (2) |
The particles are acted upon by a thermodynamic generalized force, e.g., Brownian or due to direct particle–particle interactions, and simultaneously transported by the ambient flow in the surrounding 3D fluid. Thus, in the overdamped limit we approximate
| v = Γf + u, | (3) |
 | (4) |
Notice that ![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) is the Oseen tensor for the 3D flow, even though only its evaluation at points of the monolayer plane (z = z′ = 0) is required. The mean-field-like approximations underlying eqn (2)–(4) usually imply a restriction to the “macroscopic” regime of large scales and long times (see ESI, Section 1†).
is the Oseen tensor for the 3D flow, even though only its evaluation at points of the monolayer plane (z = z′ = 0) is required. The mean-field-like approximations underlying eqn (2)–(4) usually imply a restriction to the “macroscopic” regime of large scales and long times (see ESI, Section 1†).
In the absence of external force fields, the homogeneous, stationary state, ρ(r,t) = ρhom, f(r,t) = 0, u(r,t) = 0, is a possible solution of eqn (2)–(4). By linearizing them about the homogeneous state, one obtains an equation for the evolution of the perturbation δρ(r,t) = ρ(r,t) − ρhom,
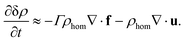 | (5) |
In this linear approximation, f can be approximated as a linear functional of ∇δρ in general, so that the first term describes the decay (or growth, in cases of instability) of density fluctuations driven by the force field. The second term accounts for the effect of HI and the key point is to note that ∇ · u ≠ 0 in the 2D layer, that is, the ambient flow at the plane z = 0 induces compression and dilution of the colloidal fluid, although the full 3D ambient flow is not compressible. This is at variance with the phenomenology when ∇ · u = 0 (absence of confinement or full confinement to 2D), under which conditions the effect of the HI appears only as a nonlinear coupling (advection). By introducing the 2D Fourier transform of the fields, eqn (5) can be cast into the form of eqn (1) with D(k) = [1 + g(k)]D0(k) (see ESI, Section 2†). Here D0(k), defined from fk ≈ [D0(k)/Γρhom](−ikδρk), is the diffusion coefficient in the absence of hydrodynamic couplings, the latter being accounted for by the function
 | (6) |
The anomalous diffusion is illustrated by means of two physically relevant models lying at opposite extremes. The first case is an ideal gas (no direct interparticle force), for which f = −kBT∇ ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ and D0(k) = ΓkBT. The Green function G(r,t) of eqn (1) is (see ESI, Section 3†)
ρ and D0(k) = ΓkBT. The Green function G(r,t) of eqn (1) is (see ESI, Section 3†)
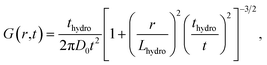 | (7) |
The second case is a system of colloidal particles trapped by wetting forces at the interface between two fluids. They deform the interface slightly and an effective mutual interaction of capillary origin arises (see, e.g., ref. 17). In the simplest model (two-body force between capillary monopoles), the pairwise, attractive interaction potential is proportional to the Bessel function K0(r/λ), dependent on the capillary length λ. When λ → ∞, this reduces to the Newtonian gravitational potential in 2D. For realistic configurations (λ ∼ mm, typical particle size ∼ μm), the attraction is extremely long-ranged and one can use the mean-field approximation to compute the force f and derive (see ESI, Section 4†)
 | (8) |
Here, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) is a characteristic time scale and
is a characteristic time scale and ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) −1 is a characteristic length scale. Eqn (8) predicts a clustering instability dominated by the large scales (D0(k) < 0 if k <
−1 is a characteristic length scale. Eqn (8) predicts a clustering instability dominated by the large scales (D0(k) < 0 if k < ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) ) provided λ
) provided λ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) > 1. For these modes, HI-induced faster evolution is predicted too because, regarding the ambient flow, one can dismiss the tiny interfacial deformation, so that the Oseen tensor in the monolayer plane (see eqn (4)) holds either asymptotically for large separations, or exactly in the absence of a viscosity contrast at the fluid interface.19
> 1. For these modes, HI-induced faster evolution is predicted too because, regarding the ambient flow, one can dismiss the tiny interfacial deformation, so that the Oseen tensor in the monolayer plane (see eqn (4)) holds either asymptotically for large separations, or exactly in the absence of a viscosity contrast at the fluid interface.19
Results from simulations
The preceding theoretical analysis has been tested and extended beyond the linear regime by means of simulations of a colloidal monolayer. As our workhorse simulation method, we choose quasi-2D Brownian Dynamics (BD) simulations.18 We include HI, truncated at the two-body level, through the Rotne–Prager approximation, leading to a truncated Stokesian Dynamics (tSD)20 that already incorporates the Oseen tensor and thus the physics discussed in the previous paragraphs (see ESI, Section 5.1†). The tSD simulations are validated using a combined 3D multicomponent lattice Boltzmann (LB) and Molecular Dynamics algorithm21 which includes HI at the many-body level (see ESI, Section 5.2†). Using these simulation techniques, we illustrate the effect of HI on two aspects of the dynamics in the capillary collapse scenario and, as a third example, on the diffusional behavior in a 2D ideal gas of colloidal particles:(i) HI-enhanced diffusion coefficient in capillary collapse: we check the linear prediction ρk(t) ∝ exp (−D(k)k2t) from eqn (1) for capillary monopoles using tSD simulations. As Fig. 1 illustrates, simulation results are described very well by theory and clearly show the enhancement due to the 1/k divergence of the diffusion coefficient compared with the corresponding results without HI. (The deviations at large values of k/![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) are due to nonlinear effects, and to corrections to mean-field from the short-range repulsion.)
are due to nonlinear effects, and to corrections to mean-field from the short-range repulsion.)
 | ||
| Fig. 1 Growth of ρk(t) from tSD simulations (symbols) and from linear theory, eqn (1) and (8) (thick lines; thin lines in the absence of HI). See ESI, Section 5.3.† | ||
(ii) Speedup of nonlinear capillary collapse: a particularly simple limit case of the instability corresponds to ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) , λ → ∞ in eqn (8) (dubbed “cold collapse” in 2D Newtonian gravity), allowing for an exact solution of the nonlinear evolution equations in the absence of HI:18 an initially homogeneous circular patch of particles (top-hat profile) remains top-hat during the evolution towards the simultaneous collapse of all the particles at the center at a time t =
, λ → ∞ in eqn (8) (dubbed “cold collapse” in 2D Newtonian gravity), allowing for an exact solution of the nonlinear evolution equations in the absence of HI:18 an initially homogeneous circular patch of particles (top-hat profile) remains top-hat during the evolution towards the simultaneous collapse of all the particles at the center at a time t = ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) . Fig. 2 addresses the effect of HI on this solution by means of tSD and LB simulations: due to the faster dynamics of the low-k modes induced by HI, the collapse occurs earlier and the top-hat profile is destroyed, with a faster increase of density at the center (clearly seen at time t/
. Fig. 2 addresses the effect of HI on this solution by means of tSD and LB simulations: due to the faster dynamics of the low-k modes induced by HI, the collapse occurs earlier and the top-hat profile is destroyed, with a faster increase of density at the center (clearly seen at time t/![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 0.5), until close-packing effects become important (at t/
= 0.5), until close-packing effects become important (at t/![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 0.8) and halt the collapse. The agreement between the results from tSD and LB is reassuring that the phenomenological effect by HI is captured already by the Oseen approximation. When the capillary attraction is screened (λ < initial patch radius), the collapse develops a shockwave-like feature at the outer rim.22 As illustrated by Fig. 3, the incorporation of HI does not alter this qualitative spatial structure but the faster time evolution towards the collapse is very prominent.
= 0.8) and halt the collapse. The agreement between the results from tSD and LB is reassuring that the phenomenological effect by HI is captured already by the Oseen approximation. When the capillary attraction is screened (λ < initial patch radius), the collapse develops a shockwave-like feature at the outer rim.22 As illustrated by Fig. 3, the incorporation of HI does not alter this qualitative spatial structure but the faster time evolution towards the collapse is very prominent.
 | ||
| Fig. 2 Collapse of an initial top-hat profile (radius R, density ρ0, see ESI, Section 5.3†) for 2D gravity (λ → ∞) without (dashed line, from theory) and with HI (symbols, from tSD and LB simulations). | ||
 | ||
| Fig. 3 Same as Fig. 2 but for a larger system (see ESI, Section 5.3†) and screened capillary attraction (λ < ∞) without (open symbols, from BD simulations) and with HI (filled symbols, from tSD simulations). | ||
(iii) Anomalous diffusion in an ideal gas: we have considered an initial top-hat profile immersed in a homogeneous background. Despite the absence of (static) interactions, the evolution is affected by the HI if a nonvanishing hydrodynamic radius rH of the particles is assumed. This corresponds to the idealized case of, e.g., mutually interpenetrable polymeric particles whose radius of gyration defines rH. Fig. 4 shows the effect of HI by means of simulations and the numerical solution of eqn (2)–(4). One can observe how the HI reduce the diffusion time and induce the development of a tail consistent with the r−3 decay predicted by eqn (7).
 | ||
| Fig. 4 Diffusion of a top-hat overdensity of ideal gas without (filled symbols, from BD simulations) and with HI (open symbols, from tSD simulations). Lines represent the numerical solution of eqn (2)–(4). For simulation parameters, see ESI, Section 5.3.† | ||
Discussion and conclusions
The singularity in D(k) of a monolayer is derived from a 3D flow which affects the particle dynamics already at the linear level because it is compressible in the plane of colloidal motion. Thus, it is distinct from the well known divergence of the diffusion coefficient in purely 2D systems. The latter is related to the Stokes paradox and due to a long-time tail in the velocity autocorrelation, induced by the nonlinear coupling of the particle motion with the build-up in time of a 2D incompressible flow. Likewise, it differs from the divergence in lateral diffusion in fluid membranes, related also to the Stokes paradox for the 2D incompressible flow inside the membrane.13 The singularity in D(k) is a sole consequence of the partial confinement and is a quite robust result, being qualitatively independent of the specific properties (strength, range) of the effective, static interaction between the particles. Similarly, the model can be applied to the dynamics of particles restricted to a line, and eqn (6) predicts 1D anomalous collective diffusion, D(k → 0) ∼ ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k (see ESI, Section 2†). Thus, dynamic signatures of this singularity can be expected wherever the conditions of restricted colloidal motion and unrestricted hydrodynamic interactions are met. Possibly related to our results on the collective long-time diffusion is the experimental observation of an enhanced collective short-time‡ diffusion reported in ref. 23. We also note the experimental observation of an enhancement of self diffusion in monolayers,10,24 which the authors interpret as a consequence of HI mediated by 3D flow.
k (see ESI, Section 2†). Thus, dynamic signatures of this singularity can be expected wherever the conditions of restricted colloidal motion and unrestricted hydrodynamic interactions are met. Possibly related to our results on the collective long-time diffusion is the experimental observation of an enhanced collective short-time‡ diffusion reported in ref. 23. We also note the experimental observation of an enhancement of self diffusion in monolayers,10,24 which the authors interpret as a consequence of HI mediated by 3D flow.
In conclusion, under partial confinement, i.e., colloidal motion restricted to a plane or a line but with hydrodynamic interactions originating from 3D flow of a surrounding fluid, peculiar collective diffusion properties emerge. Using a mean-field model, we have identified a singularity in the collective long-time diffusion coefficient responsible for anomalous diffusion. The dominating dynamical effect of this singularity has been illustrated by simulation examples of an ideal gas (dilute limit) and a monolayer of capillary monopoles at a fluid interface (long-ranged interparticle attraction) obtained with effectively 2D Stokesian dynamics truncated at the two-body level and with 3D Lattice-Boltzmann/Molecular Dynamics simulations.
Acknowledgements
A.D. acknowledges support by the Spanish Government through Grants AIB2010DE-00263 and FIS2011-24460 (partially financed by FEDER funds). Part of the work of J.B. has been performed under the HPC-Europa2 project (project number: 228398) with the support of the European Commission – Capacities Area – Research Infrastructure.References
- J. Lippincott-Schwartz, E. Snapp and A. Kenworthy, Nat. Rev. Mol. Cell Biol., 2001, 2, 444 CrossRef CAS PubMed.
- R. Metzler and J. Klafter, Phys. Rep., 2000, 339, 1 CrossRef CAS.
- X.-L. Wu and A. Libchaber, Phys. Rev. Lett., 2000, 84, 3017 CrossRef CAS.
- F. Matthäus, M. Jagodic and J. Dobnikar, Biophys. J., 2009, 97, 946 CrossRef PubMed.
- A. M. Lacasta, J. M. Sancho, A. H. Romero, I. M. Sokolov and K. Lindenberg, Phys. Rev. E, 2004, 70, 051104 CrossRef CAS.
- H. Chate, F. Ginelli, G. Gregoire and F. Raynaud, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 046113 CrossRef.
- R. Pesché and G. Nägele, Europhys. Lett., 2000, 57, 584 ( Phys. Rev. E , 2000 , 62 , 5432 ) CrossRef.
- G. Nägele, M. Kollmann, R. Pesché and A. J. Banchio, Mol. Phys., 2002, 100, 2921 CrossRef.
- J. W. Swan and J. F. Brady, J. Fluid Mech., 2011, 687, 254 CrossRef CAS.
- B. Rinn, K. Zahn, P. Maass and G. Maret, Europhys. Lett., 1999, 46, 537 CrossRef CAS.
- B. Cichocki, M. L. Ekiel-Jeżewska, G. Nägele and E. Wajnryb, Europhys. Lett., 2004, 67, 383 CrossRef CAS.
- F. Höfling and T. Franosch, Rep. Prog. Phys., 2013, 76, 046602 CrossRef PubMed.
- P. Saffman, J. Fluid Mech., 1976, 73, 593 CrossRef.
- S. Ramachandran, S. Komura and G. Gompper, Europhys. Lett., 2010, 89, 56001 CrossRef.
- P. Pieranski, Phys. Rev. Lett., 1980, 45, 569 CrossRef CAS.
- C. Lutz, M. Kollmann and C. Bechinger, Phys. Rev. Lett., 2004, 93, 026001 CrossRef.
- P. A. Kralchevsky and K. Nagayama, Adv. Colloid Interface Sci., 2000, 85, 145 CrossRef CAS.
- J. Bleibel, A. Domínguez, M. Oettel and S. Dietrich, Eur. Phys. J. E, 2011, 34, 125 CrossRef CAS PubMed.
- R. B. Jones, B. U. Felderhof and J. M. Deutch, Macromolecules, 1975, 8, 680 CrossRef CAS.
- J. F. Brady and G. Bossis, Annu. Rev. Fluid Mech., 1988, 20, 111 CrossRef.
- F. Jansen and J. Harting, Phys. Rev. E, 2011, 83, 046707 CrossRef.
- J. Bleibel, S. Dietrich, A. Domínguez and M. Oettel, Phys. Rev. Lett., 2011, 107, 128302 CrossRef CAS.
- B. Lin, S. A. Rice and D. A. Weitz, Phys. Rev. E, 1995, 51, 423 CrossRef CAS; B. Lin, B. Cui, X. Xu, R. Zangi, H. Diamant and S. A. Rice, Phys. Rev. E, 2014, 89, 022303 CrossRef.
- K. Zahn, J. M. Méndez-Alcaraz and G. Maret, Phys. Rev. Lett., 1997, 79, 175 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3sm53043d |
| ‡ “Short-time” meaning a time much shorter than the diffusion time over a distance of the order of the mean interparticle separation. |
| This journal is © The Royal Society of Chemistry 2014 |

