Chemotactic clusters in confined run-and-tumble bacteria: a numerical investigation†
E. J.
Marsden
*a,
C.
Valeriani
b,
I.
Sullivan
a,
M. E.
Cates
a and
D.
Marenduzzo
a
aSUPA, School of Physics and Astronomy, University of Edinburgh, Mayfield Road, Edinburgh EH9 3JZ, UK. E-mail: e.j.marsden@sms.ed.ac.uk
bDepartamento de Quimica Fisica, Facultad de Ciencias Quimicas, Universidad Complutense de Madrid, 28040 Madrid, Spain
First published on 5th November 2013
Abstract
We present a simulation study of pattern formation in an ensemble of chemotactic run-and-tumble bacteria, focussing on the effect of spatial confinement, either within traps or inside a maze. These geometries are inspired by previous experiments probing pattern formation in chemotactic strains of E. coli under these conditions. Our main result is that a microscopic model of chemotactic run-and-tumble particles which themselves secrete a chemoattractant is able to reproduce the main experimental observations, namely the formation of bacterial aggregates within traps and in dead ends of a maze. Our simulations also demonstrate that stochasticity plays a key role and leads to a hysteretic response when the chemotactic sensitivity is varied. We compare the results of run-and-tumble particles with simulations performed with a simplified version of the model where the active particles are smooth swimmers which respond to chemotactic gradients by rotating towards the source of chemoattractant. This class of models leads again to aggregation, but with quantitative and qualitative differences in, for instance, the size and shape of clusters.
1 Introduction
A large number of bacterial species possess the ability to move actively through their environment, which is generally referred to as ‘motility’. In addition, many of these motile bacteria can direct this motion towards favourable chemical environments, a behaviour known as ‘chemotaxis’. This allows bacteria to seek out beneficial substances such as nutrients and oxygen (‘attractants’), and avoid poisons (‘repellents’), which generally leads to an evolutionary advantage. Due to its relative simplicity and the extensive data gathered on it, the best studied example of such bacteria is Escherichia coli, or E. coli (see ref. 1 for an overview of the organism).E. coli is a rod-shaped bacterium around 2 μm long and 1 μm wide,2 with several (typically four) flagella protruding from its surface, which have rotating motors at their base.3 If a sufficient number of these motors rotate counter-clockwise, the flagella form a bundle and propel the bacterium forward along a roughly straight path. If some fraction of the motors change direction this bundle breaks apart, the flagella move independently, and the bacterium rotates randomly while its centre of mass stays approximately stationary. The swimming of motile E. coli can therefore be seen as a sequence of switches between translational motion with negligible rotation (commonly referred to as a ‘run’), and random rotation with little translational motion (a ‘tumble’). This form of motion is referred to as ‘run-and-tumble’ dynamics.4–6
Although chemotaxis occurs in a wide variety of organisms, its manifestation in bacteria is a particularly interesting case as they are not physically large enough to sense spatial gradients of chemicals directly,7,8 in contrast to larger, eukaryotic organisms,9,10 therefore they require complex signal processing in order to get where they want to go.
In the case of E. coli, chemotaxis is achieved by modulating the amount of time the bacteria spends in the running or tumbling state. Under normal conditions a run typically lasts around 1 second, while a tumble lasts around 0.1 seconds.5 If, during a run, the bacterium senses it is moving along a favourable direction, this acts to decrease the probability of tumbling. This means that runs along favourable gradients will on average last longer than those which are not, causing a net drift towards regions which are high in the concentration of the attractant (or low in that of the repellent).
Often, experiments probing bacterial chemotaxis have focused on the response to chemical gradients imposed externally.11–13 However, in other cases, which are most relevant to our work, the chemicals sensed by the cells may actually be secreted by the bacteria themselves – experiments probing this second kind of chemotaxis are those of ref. 14–17, which we will discuss in more detail later. Such chemical signalling, or self-chemotaxis, is to some extent akin to quorum sensing (see ref. 18 for an overview of this type of response). In simplistic terms, one may view quorum sensing as providing bacteria with the local population density, while self-chemotaxis provides them with knowledge of the local density gradient – the latter allows them to find each other, while the former tells them when they have done so. It is believed that the information gathered through these processes is used in practice to trigger population-dependent behaviour such as virulence and biofilm formation.19–21
Here we carry out numerical simulations of particles undergoing a simplified form of run-and-tumble motion with a chemotactic response, in environments similar to those used in the experiments of Park et al.16,17 where the behaviour of a strain of self-chemotactic bacteria in confinement was studied within a microfluidic chamber. In particular, the experiments considered are (i) a simple quasi-two-dimensional geometry in which confinement was realised via an array of square traps with a small opening on one side; and (ii) a more complicated case in which bacteria moved through a microfabricated maze. We compare the behaviour found by our model run-and-tumble bacteria in both geometries, finding good agreement with the experimental observations. With respect to previous work employing a mean-field continuum description of both chemical concentrations and bacterial population,22,23 our approach is more microscopic and provides an insight into the effect of fluctuations on the bacterial patterning.
Our main model builds on the experimental observation that the tumble time depends on the history of chemoattractant concentrations via a memory kernel; we also compare the results to two simplified models where chemotaxis is more crudely represented as a gradient-dependent bias in the propulsion direction. We find that, while superficially similar, the two models have sharp quantitative differences, for instance in the size of the microbial clusters. In a third model we also include an additional Vicsek-like term24 in order to investigate the effects of adding explicit inter-particle aligning interactions, which could be relevant to the case of confined bacterial swarms.25,26
Our work is organised as follows: in Section 2, we introduce the three models which we employ in the simulations. In Section 3, we present our results, focussing mainly on the more realistic run-and-tumble model, and discussing the other two models more briefly for comparative purposes. For each case, we consider a set of progressively more complicated geometries: first we study pattern formation in the absence of boundaries, then we study active particle clustering with one or more traps, and finally we turn to the topologically most complex case of a randomly generated maze. As explained above, all these situations have an experimental counterpart which has been studied in the past.16,17
2 Theory
2.1 Particle dynamics
Three distinct models have been investigated: the first is a simplified model of run-and-tumble motion similar to that described by Schnitzer et al.27 The second is a simpler model in which the chemoattractant acts as a potential which applies a force-like attraction to active brownian particles. The third model is exactly equivalent to the second, with an additional Vicsek-like24 alignment interaction with neighbouring particles. We now turn to a detailed description of each of these models, and the associated rules. We work in two dimensions throughout. The first model is biologically realistic at the microscopic level, while the other two provide comparative models of chemotaxis. Comparison of a biologically inspired model with others makes it possible to distinguish features common to all forms, and those specific to the run and tumble variety performed by bacteria. | (1) |
Tumbles occur at a rate α; it is this rate which is varied linearly in order to model a chemotactic response. In the absence of chemotactic gradients tumbling occurs at a rate α0. A one-sided response is used, where α may decrease when the particle is moving in a favourable direction, but not increase when moving in an unfavourable one. This is the experimentally relevant case for E. coli.5,29,30 Explicitly, the tumble rate at time t is given by
 | (2) |
 | (3) |
 | (4) |
The kernel's shape is shown in Fig. 1. The model we have described will be referred to as the Run-and-Tumble (RT) model in the following.
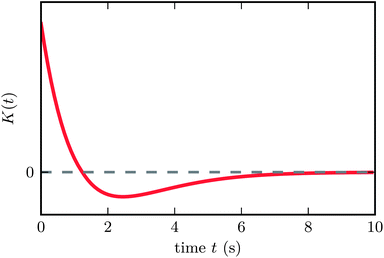 | ||
| Fig. 1 Bacterial memory kernel as proposed by Clark and Grant.31 The kernel has zero net area, allowing for effective chemotaxis independent of the absolute chemical concentration. | ||
 | (5) |
 | (6) |
The rotation matrix R(θ) acts to give the particles a chemotaxis-free rotational diffusion constant Dr,F. This value was chosen to give the CF and RT particles equal chemotaxis-free diffusion, which for our choice of α0 = 1 s−1 requires Dr,F = 2 rad2 s−1.
This model will be referred to as the ‘chemotactic force’ (CF) model.
 | (7) |
The velocity at the next time step is then chosen as
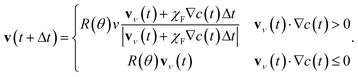 | (8) |
It should be noted that the order in which these two processes are applied (velocity alignment, and chemotactic force) is potentially important. Here we have chosen to apply them in the order stated, however it appears our qualitative results are not order-dependent.
In the simulations below a neighborhood radius of rν = 3 μm (equivalent to ∼3 times the bacterial size) is used, as this is an approximate length scale on which explicit inter-bacterial interactions such as the above mentioned steric effects and hydrodynamics may be expected to be significant.
This model will be referred to as the Chemotactic Force with Vicsek alignment (CFV) model.
 | (9) |
In all models a particle speed of v = 20 μm s−1, which is realistic for E. coli, is used. It should be noted that inter-particle collisions are not considered.
2.2 Chemoattractant dynamics
The concentration of chemoattractant is modelled as a field obeying the following reaction–diffusion equation, | (10) |
For chemoattractant dynamics, the following parameters were used in all simulations: Dc = 20 μm2 s−1, ϕ = 1 s−1, δ = 0.01 s−1, c(x, t = 0) = 0 μm−2 and ρ(x, t = 0) = ρ0 = 3.5 × 10−3 μm−2. These correspond to biophysically realistic values.1,35
To validate these parameters, from (10) it can be seen that as a rough approximation (neglecting the diffusive term), at steady state  . If a bacterial cluster is ∼5ρ0, a typical concentration of chemoattractant in a cluster is 0.5 μm−2. For a typical chemoattractant decay length of 1 mm, this gives a chemotactic gradient of 0.5 × 10−3 μm−3. Taking the CF model as an example, where χF = 6000 μm4 s−3 is a typical sensitivity required for clustering, this implies a typical acceleration of 0.1v0 s−1, a sensible value.
. If a bacterial cluster is ∼5ρ0, a typical concentration of chemoattractant in a cluster is 0.5 μm−2. For a typical chemoattractant decay length of 1 mm, this gives a chemotactic gradient of 0.5 × 10−3 μm−3. Taking the CF model as an example, where χF = 6000 μm4 s−3 is a typical sensitivity required for clustering, this implies a typical acceleration of 0.1v0 s−1, a sensible value.
2.3 Choice of simulation geometries
The three models outlined above were simulated in a 2-dimensional periodic space with length L = 1200 μm. Physical obstacles were then added in order to control the environment geometry. Four distinct topologies were investigated: (a) a uniform environment without physical obstacles, in order to investigate the fundamental clustering behaviour driven by chemoattractant-mediated interactions; (b) an environment featuring a single trap-like structure similar in physical dimensions to that used in the experiments of Park et al.16,17 in order to see how such a structure affects the tendency of the particles to form and sustain clusters; (c) a similar environment featuring multiple traps, in order to introduce multiple ‘nucleation points’ for clustering and (d) a randomly generated maze, again similar to that of Park et al.16,17 with the aim of investigating cluster formation in highly complex topologies, to see whether and to what extent clusters merge and coarsen at long times.3 Results
3.1 Run and tumble model
We start by studying the dynamics of chemotactic bacteria in uniform environments. A typical snapshot from these runs is shown in Fig. 2a, where it is apparent that bacteria form aggregates – typically, these coarsen to leave a single steady state cluster, as in the figure. A representation of the dynamics of the aggregation process in a uniform environment can be viewed in ESI Movie 1.† Particles form small clusters that drift and merge into a single aggregate. The size of the final aggregate in our simulations is around 300 μm, in approximate agreement with the experimental size, as can be estimated from images by Budrene et al. (Fig. 3). The relevance of the agreement of these cluster sizes depends on the unimportance of effects such as finite-volume and quorum sensing, which we neglect, however Budrene and Berg attribute the size of their clusters solely to a chemotactically varied tumble rate, suggesting that the comparison is valid. | ||
| Fig. 3 Cluster of E. coli bacteria formed by chemotactic aggregation as imaged by Budrene et al.42 Scale bar indicates 100 μm. Copyright 2003 National Academy of Sciences, USA. | ||
First we briefly recall the mechanism behind the chemotactic aggregation, or clustering, as it occurs in our models. Due to some fluctuations, the local density of run-and-tumble particles may increase, and this leads to a localised peak in the production of chemoattractant by those particles. The resulting chemoattractant gradient acts as a funnel to drive more particles there through chemotactic sensing; this leads to even more density increase etc. This self-trapping feedback is responsible for the clustering in our simulations. A similar phenomenon has recently been well studied for populations of self-motile particles whose velocity decreases with local crowding;36–40 it is also compatible with our understanding of the way clustering occurs in experiments involving chemotaxis.
Simulations in non-uniform geometries resulted in non-uniform density distributions similar to that seen experimentally (Fig. 4). In the single-trap environment (Fig. 2b) accumulation occurred preferentially inside the trap, at higher densities than in the uniform case. In the environment featuring multiple traps (Fig. 2c), stable clusters were formed in between one trap and three traps at steady state (the specific locations of which varied between runs). This is in contrast with the experimental results seen in Fig. 4b, where all of the traps appear to exhibit a roughly equal increased bacterial density. Given that our simulations reproduced accumulation in a single trap, this might suggest that our model overestimates the length scale on which chemotaxis acts, since accumulation in one trap has an impact on behaviour in nearby traps greater than that observed experimentally. It may also be possible that uneven trap occupation would arise in environments where traps are closer together, hence interact more strongly. This could be verified by further experiments studying the effect of variations in the geometry of the microfluidic chamber where bacteria move.
 | ||
| Fig. 4 Epifluorescence images of E. coli labelled with green fluorescent protein, from.16,17 (a) Accumulation in a 250 μm × 250 μm trap from an initially uniform distribution. At 3 hours the trap density is more than seven times higher than that outside of the trap. (b) Accumulation into multiple confining traps from an initial uniform distribution. (c) Accumulation in dead ends of a maze after 3 hours from an initial uniform distribution. Copyright 2003 National Academy of Sciences, USA. | ||
Run-and-tumble particles also form clusters in the maze environment (Fig. 2d). The mazes we considered were generated randomly with the recursive backtracker algorithm.41
In all cases, we observe accumulation or self-trapping of chemotactic particles occurring in dead ends of the maze (Fig. 2d). This is again in line with the experiments.16,17 The location of the clusters varied between runs, however the number of distinct clusters formed was consistent for a given geometry.
The quantity used to measure the extent of clustering at time t was the standard deviation of the particle number density, σρ, over the unobstructed area of the system A,
 | (11) |
The obstructed area was not included in the calculation as its inclusion would artificially increase the measurement in obstructed geometries. In practice the integral was approximated as a sum, with ρ(r, t) evaluated on a grid identically to the method used when solving eqn (10), albeit with a different spatial grid size.
This quantity was made use of in characterising the system's transition between uniform and clustered states. To induce the transition we ran several simulations with the initial condition χT = 0 μm2 s. This was then increased at a constant rate to a maximum value, and then decreased at the same constant rate to χT = 0 μm2 s. The rate chosen was the minimal one which was affordable with a reasonable computational cost (50 CPU hours per run), ![[small chi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e11e.gif) T = 0.5 × 10−3 μm2 s. Three distinct runs were used in all simulations of this form; the results shown are the mean response of these runs.
T = 0.5 × 10−3 μm2 s. Three distinct runs were used in all simulations of this form; the results shown are the mean response of these runs.
Fig. 5 shows a comparison between the chemotactic aggregation observed in the uniform and trap environments, in order to verify that the latter geometry promotes clustering. When a trap is present, we distinguished between two cases: (i) that in which the cluster formed inside the trap (this is the case shown in the snapshot in Fig. 2b), and (ii) that in which aggregation occurs outside it. In agreement with experimental observation, case (i) is the more probable one.
In runs where a cluster formed in the interior of the trap, the degree of spatial inhomogeneity was around 3 times greater than in the uniform environment, and the threshold sensitivity at which clustering occurs was reduced (from χT ≃ 20 μm2 s to χT ≃ 15 μm2 s). This demonstrates that the presence of the trap significantly enhances clustering.
In the minority of runs leading to a cluster formed on an exterior wall of the trap, we find an intermediate result, with a reduced inhomogeneity compared with the interior trap case, but still larger than the case with no trap at all. This finding also suggests that clustering on a surface, or wall, requires more chemotactic sensitivity than the case of a cluster formed inside an entirely enclosed environment.
In all cases there is clear evidence of hysteresis in the behaviour – as the system approaches from a uniform state (the lower branch) a greater χT is required to induce clustering, than the value at which clusters are maintained when approaching from a non-uniform state (the upper branch). For all geometries, the uniform state, where bacteria are homogeneously distributed, corresponds to a region in the plot where σρ is independent of χT; the metastable state corresponds to an approximately linear ramp whose gradient depends on the system history; and finally the clustered state to a non-linear response which saturates as χT → ∞. In the trap environment for the typical case where particles collapse inside the trap, the system along the lower branch may be seen to be in the ‘uniform state’ for 0 μm2 s ≤ χmathrmT ≲ 15 μm2 s; the ‘metastable state’ for 15 μm2 s ≲ χT ≲ 27 μm2 s and the ‘clustered state’ for χT ≳ 27 μm2 s (Fig. 5).
The same simulations were carried out for the multiple-trap and maze environments, and the results are shown in Fig. 6. In the case of multiple traps, clustering requires roughly the same chemotactic sensitivity as in the single-trap case, however the degree of spatial inhomogeneity is reduced as a result of the competition between multiple clusters (Fig. 2c). The strength of hysteresis is similar in the two cases.
 | ||
| Fig. 6 As in Fig. 5, for single-trap runs in which particles accumulated on the trap interior (replotted from Fig. 5 for comparison), the multiple-trap environment and an environment containing a randomly generated maze. The solid and dashed lines represent increasing and decreasing χT, respectively. | ||
The maze environment also induces clustering at a similar chemotactic strength, and causes a smaller degree of inhomogeneity compared with the multiple-trap environment. Given that in the maze typically 6–8 stable clusters were formed, this supports the idea that a greater number of nucleation points results in a greater number of less populated clusters. It is interesting to note that despite the maze exhibiting less clustering when transitioning from a uniform distribution, the clusters were maintained, on decreasing χT, down to around χT = 5 μm2 s, compared with around χT = 12 μm2 s in both of the trap environments. In addition, from the greater degree of hysteresis it appears the clustered and non-clustered phases are more distinct in the maze geometry. This may be due to the presence of confining structures on multiple length scales due to the complex geometry of the maze, which might allow a cluster to adapt its size and shape as the sensitivity changes. This scenario is at variance with aggregation within a simple trap, as there the geometry introduces a single length scale.
3.2 Chemotactic force model
Typical snapshots from runs in identical environments to those used in the previous section with CF particles are shown in Fig. 7. By visual inspection, it can be seen that the typical cluster size is smaller than in the RT model, however the qualitative results are the same, i.e. bacteria self-trap in the absence of boundaries, collapse into traps and accumulate in maze dead-ends. In the latter two environments, multiple stable clusters are formed as in the RT model. Again, the cluster locations vary between runs, but a consistent number arise. Intriguingly, the CF particles can further organise within the trap geometry, preferentially accumulating within a corner. This is because the gradient which is set up if the chemoattractant is produced at a corner is larger than if established elsewhere (at least when zero-flux boundary conditions are used for its reaction–diffusion dynamics). This bias if present might be observed in microscopy experiments with chemotactic bacteria in traps of sufficient size (i.e. larger than a typical bacterial cluster). | ||
| Fig. 7 As in Fig. 2, for the CF model. | ||
To compare with the quantitative results in the RT model, we carried out similar simulations with a linear ramped chemotactic sensitivity, χF. The results for the uniform and trap environments are shown in Fig. 8. The speed of the ramp was chosen such that uniform-environment clustering was induced at a similar system time to the RT case, ![[small chi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e11e.gif) F = 0.125 μm4 s−3.
F = 0.125 μm4 s−3.
 | ||
Fig. 8 Spatial deviation of CF particle density, σρ under the same conditions as described in Fig. 5, with ![[small chi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e11e.gif) F = 0.125 μm4 s−3. The top curve was obtained in an environment containing a single trap (which the particles collapse inside); the bottom curve in a uniform environment containing no physical obstacles. F = 0.125 μm4 s−3. The top curve was obtained in an environment containing a single trap (which the particles collapse inside); the bottom curve in a uniform environment containing no physical obstacles. | ||
Although both χT and χF parametrise the strength of chemotaxis in the RT and CF models, respectively, there is not a simple mapping relating them. Fig. 9 shows a calibration curve of the typical relative drift speed of both particle types in a linear chemical ramp, as the two parameters are varied. From this it can be seen that the mapping is non-linear above around χF/T = 0.2, and as such the parameters cannot be directly compared – this should be borne in mind when comparing results between models.
As for the RT particles, the trap very much affects the physics of the clustering: in its presence clusters form at a reduced chemotactic sensitivity with the uniform environment, and we once again observe an increased spatial nonhomogeneity, quantified by σρ. There are however quantitative differences between the response of the CF and RT models. Most notably, the homogeneous region (where no clusters form) is smaller than in the RT model, while the metastable region, where we observe hysteresis, is enhanced. This phenomenology is more dramatic in the case of the trap environment, where it is difficult to identify a homogeneous phase when decreasing χF. When compared with the RT case, in the CF model the clustered state also quickly approaches a saturated state where σρ is approximately constant.
Finally, no clustering was observed on trap exteriors with the CF model – all runs result in population collapse into the trap interior. The CF model therefore leads to an enhanced effect of the geometry on the patterning; as mentioned in the introduction, we expect however the RT model to be more faithful quantitatively to bacteria, as the microscopic rules are closer to our current view of bacterial chemotaxis.
The hysteresis curves obtained in more complex topologies for the CF model are shown in Fig. 10. In the case of multiple traps, the number and location of the clusters changed multiple times in the course of running each simulation, unlike in the RT model, where the initial clusters which formed persisted throughout each run. Otherwise the trend is similar to the RT model, in that the addition of nucleation points decreases the spatial particle density deviation. A difference may be seen in that the clustered state appears to be more stable in the trap environments than in the maze (observable from the lower threshold for cluster breakdown in the former case) – opposite to that seen for RT particles. This is presumably because the clusters formed in the CF model are smaller than those in the RT model (compare the scales of σρ in, for instance, Fig. 6 and 10).
 | ||
| Fig. 10 As in Fig. 8 for the single trap, multiple trap and maze environments. As previously, solid and dashed lines represent increasing and decreasing χF, respectively. | ||
3.3 Chemotactic force with Vicsek interaction
We finally briefly discuss the chemotactic force model with Vicsek alignment (CFV model). Snapshots showing the qualitative behaviour of the CFV model in the uniform, single/multiple trap and maze are shown in Fig. 11. Once more, the geometric confinement induced an increase in the self-trapping of the chemotactic particles. We also see that the CFV model also qualitatively reproduces all the experimental trends.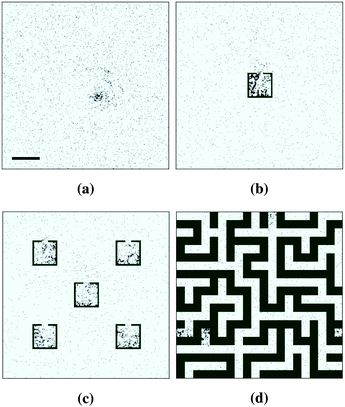 | ||
| Fig. 11 As in Fig. 2, for the CFV model. | ||
Intriguingly, in this case the balance between the occupation of each of the traps in the multiple trap environment is more even than we observed in the RT and CF models. It should be kept in mind that the parameter range in which we use the CFV model flocks are very small in size, because the ‘Vicsek’ interaction range within which particles attempt to align their velocity is only a few times larger than the size of a bacterium (and much smaller than the size of the trap or the channels in the maze). This is the relevant case for suspensions of bacterial swimmers which can likely orient with respect to each other only through steric or hydrodynamic interactions.43,44
Increasing the alignment range, rν, or decreasing the noise, does not generally destroy the formation of clusters, however the preference for dead ends is no longer observed (Fig. 12). This may be relevant to other microorganisms, as flocking can nevertheless lead to rather exotic dynamics (ESI Movie 2† shows the meandering of a flock of CFV particles within a maze).
4 Conclusion
We have presented computer simulations of the dynamics and pattern formation of a suspension of self-propelled particles which sense gradients in a chemoattractant which they produce. This situation is relevant to pattern formation in strains of E. coli, which regulate their tumbling rate according to the local gradients in concentrations of chemicals such as aspartate,45 which they can excrete.14 We focus on the interplay between chemotactic pattern formation and geometric confinement, either in regular arrays of traps or within complicated mazes. Both these situations were recently considered experimentally, leading to the broad observation that they can enhance clustering in the bacterial populations.16,17Our simulations are microscopic and, unlike previous models employing mean-field reaction diffusion equations for the bacterial population,22,23 they can capture the effect of fluctuations and stochasticity. This is important because the pattern formation which we observe is a chemotactic clustering which may be viewed as a nonequilibrium phase transition, whose character and onset may be potentially affected by noise in a major way. Our model also captures the key microscopic details of run-and-tumble motion, and the important experimental observation that the way bacteria respond to a chemical gradient is typically by altering their tumble rate, reducing it when they move up a gradient of chemoattractant.
Our main result is that the models recreate the patterning found in experiments with chemotactic bacterial strains (of E. coli) in confined or topologically complex environments.16,17 Thus, we find that bacteria spontaneously enter into the traps and aggregate there, and that they cluster into dead ends of mazes. The cluster size compares favourably with that observed experimentally, and is in the hundred of microns range. Our model further predicts that the patterning is akin to a first order phase transition, between a homogeneous and a clustered state. The first order, or discontinuous, nature of the transition manifests itself in the presence of a large hysteresis when we track the inhomogeneity in bacterial density (which increases as the extent of aggregation rises) versus the chemotactic sensitivity of the simulated bacterial strain. Our simulations finally suggest that run-and-tumble particles are particularly susceptible to the geometry of the environment: when multiple traps are present, or when they are confined within a maze, run-and-tumble swimmers form multiple clusters which fail to coarsen, presumably as they are too far from each other and they cannot meet easily in view of the underlying geometry. In the multiple trap case, we also see that there is a significant amount of cross-talk between different nearby traps, which leads to an inhomogeneity in the occupation of each of the trap. This has currently no experimental parallel, and we suggest that it would be interesting to systematically vary the distance between traps in microfluidic geometries to look for such fluctuation-dominated competition between chemotactic clusters.
Moreover, by comparing our microscopic model of run-and-tumble swimmers to simplified models in which bacteria simply tend to swim up chemoattractant gradients, we can single out effects which are unique to the run-and-tumble dynamics. In particular, we showed that, while all three models can broadly, and qualitatively, reproduce the experimental finding that chemotactic strains cluster within traps and in maze dead ends, there are important quantitative differences between the models we considered. Most notably, the cluster size is significantly smaller if chemotaxis simply drives bacterial motion, rather than tuning the tumble rate in an asymmetric way. In the ‘chemotactic force’ model where active particles align along the chemoattractant gradient (with some noise), clusters are seen to migrate towards the corners when they form inside a trap – again, it would be interesting to design experiments which observe the morphology of bacterial aggregates in traps of sufficient size, to confirm or falsify this simpler model. Finally, we have demonstrated that aligning interactions do not appreciably alter this phenomenology, at least in the regime in which the range over which particles align with each other is of the order of the size of a few bacteria, which is the relevant case when alignment arises due to steric or hydrodynamic interactions.
We acknowledge EPSRC for funding. MEC holds a Royal Society Research Professorship. CV acknowledges financial support from a Juan de la Cierva Fellowship, from the Marie Curie Integration Grant PCIG-GA-2011-303941 ANISOKINEQ, and from the National Project FIS2010-16159.
References
- H. C. Berg, E. coli in Motion, Springer Verlag, 2004 Search PubMed.
- T. H. Kim, S. H. Jung and K. H. Cho, BioSystems, 2008, 91, 171–182 CrossRef CAS PubMed.
- M. J. Tindall, S. L. Porter, P. K. Maini, G. Gaglia and J. P. Armitage, Bull. Math. Biol., 2008, 70, 1525–1569 CrossRef CAS PubMed.
- J. T. Locsei, J. Math. Biol., 2007, 55, 41–60 CrossRef CAS PubMed.
- D. V. Nicolau, J. P. Armitage and P. K. Maini, Comput. Biol. Chem., 2009, 33, 269–274 CrossRef CAS PubMed.
- J. Tailleur and M. E. Cates, Phys. Rev. Lett., 2008, 100, 218103 CrossRef CAS.
- C. V. Rao, G. D. Glekas and G. W. Ordal, Trends Microbiol., 2008, 16, 480–487 CrossRef CAS PubMed.
- A. Sengupta, S. van Teeffelen and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 31122 CrossRef.
- A. Levchenko and P. A. Iglesias, Biophys. J., 2002, 82, 50–63 CrossRef CAS.
- R. Erban and H. G. Othmer, SIAM J. Appl. Math., 2004, 65, 361–391 CrossRef.
- Y. V. Kalinin, S. Neumann, V. Sourjik and M. Wu, J. Bacteriol., 2010, 192, 1796–1800 CrossRef CAS PubMed.
- H. C. Berg and L. Turner, Biophys. J., 1990, 58, 919–930 CrossRef CAS.
- Y. Tu, T. S. Shimizu and H. C. Berg, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 14855 CrossRef CAS PubMed.
- E. O. Budrene and H. C. Berg, Nature, 1991, 349, 630 CrossRef CAS PubMed.
- D. E. Woodward, R. Tyson, M. R. Myerscough and J. D. Murray, Biophys. J., 1995, 68, 2181–2189 CrossRef CAS.
- S. Park, P. M. Wolanin, E. A. Yuzbashyan, P. Silberzan, J. B. Stock and R. H. Austin, Science, 2003, 301, 188 CrossRef CAS PubMed.
- S. Park, P. M. Wolanin, E. A. Yuzbashyan, H. Lin, N. C. Darnton, J. B. Stock, P. Silberzan and R. H. Austin, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 13910 CrossRef CAS PubMed.
- C. M. Waters and B. L. Bassler, Annu. Rev. Cell Dev. Biol., 2005, 21, 319–346 CrossRef CAS PubMed.
- M. B. Miller and B. L. Bassler, Annu. Rev. Microbiol., 2001, 55, 165–199 CrossRef CAS PubMed.
- M. G. Surette and B. L. Bassler, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 7046 CrossRef CAS.
- B. L. Bassler, Cell, 2002, 109, 421–424 CrossRef CAS.
- M. P. Brenner, L. S. Levitov and E. O. Budrene, Biophys. J., 1998, 74, 1677–1693 CrossRef CAS.
- Y. Tsori and P. G. de Gennes, Europhys. Lett., 2004, 66, 599 CrossRef CAS.
- T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen and O. Shochet, Phys. Rev. Lett., 1995, 75, 1226–1229 CrossRef CAS.
- N. C. Darnton, L. Turner, S. Rojevsky and H. C. Berg, Biophys. J., 2010, 98, 2082–2090 CrossRef CAS PubMed.
- H. H. Wensink, J. o. r. Dunkel, S. Heidenreich, K. Drescher, R. E. Goldstein, H. Löwen and J. M. Yeomans, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 14308–14313 CrossRef CAS PubMed.
- M. J. Schnitzer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 2553 CrossRef CAS.
- J. Saragosti, V. Calvez, N. Bournaveas, B. Perthame, A. Buguin and P. Silberzan, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16235–16240 CrossRef CAS PubMed.
- M. E. Cates, Rep. Prog. Phys., 2012, 75, 42601 CrossRef CAS PubMed.
- N. Vladimirov and V. Sourjik, Biol. Chem., 2009, 390, 1097–1104 CrossRef CAS PubMed.
- D. A. Clark and L. C. Grant, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9150 CrossRef CAS PubMed.
- V. Sourjik and H. C. Berg, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 123 CrossRef CAS PubMed.
- P. Galajda, J. E. Keymer, P. Chaikin and R. H. Austin, J. Bacteriol., 2007, 189, 8704–8707 CrossRef CAS PubMed.
- M. B. Wan and C. O. Reichhardt, Phys. Rev. Lett., 2008, 4–8 Search PubMed.
- J. D. Murray, Mathematical Biology, Springer, 2002, vol. 2 Search PubMed.
- F. D. C. Farrell, M. C. Marchetti, D. Marenduzzo and J. Tailleur, Phys. Rev. Lett., 2012, 108, 248101 CrossRef CAS.
- Y. Fily and M. C. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef.
- S. Henkes, Y. Fily and M. C. Marchetti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 40301 CrossRef.
- M. E. Cates, D. Marenduzzo, I. Pagonabarraga and J. Tailleur, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11715–11720 CrossRef CAS PubMed.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 55701 CrossRef.
- M. Foltin, Ph.D thesis, Masaryk University Faculty of Informatics, 2008.
- N. Mittal, E. O. Budrene, M. P. Brenner and A. V. Oudenaarden, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 13259–13263 CrossRef CAS PubMed.
- A. Baskaran and M. C. Marchetti, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15567–15572 CrossRef CAS PubMed.
- L. H. Cisneros, J. O. Kessler, S. Ganguly and R. E. Goldstein, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 61907 CrossRef.
- H. C. Berg and D. A. Brown, Nature, 1972, 239, 500 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c3sm52358f |
| This journal is © The Royal Society of Chemistry 2014 |




