Strong dynamical effects during stick-slip adhesive peeling
Marie-Julie
Dalbe
*ab,
Stéphane
Santucci
a,
Pierre-Philippe
Cortet
c and
Loïc
Vanel
b
aLaboratoire de Physique de l'ENS Lyon, CNRS and Université de Lyon, France. E-mail: mariejulie.dalbe@ens-lyon.fr; stephane.santucci@ens-lyon.fr
bInstitut Lumière Matière, UMR5306 Université Lyon 1-CNRS, Université de Lyon, France. E-mail: loic.vanel@univ-lyon1.fr
cLaboratoire FAST, CNRS, Univ. Paris Sud, France. E-mail: ppcortet@fast.u-psud.fr
First published on 16th October 2013
Abstract
We consider the classical problem of the stick-slip dynamics observed when peeling a roller adhesive tape at a constant velocity. From fast imaging recordings, we extract the dependence of the stick and slip phase durations on the imposed peeling velocity and peeled ribbon length. Predictions of Maugis and Barquins [in Adhesion 12, edited by K. W. Allen, Elsevier ASP, London, 1988, pp. 205–222] based on a quasistatic assumption succeed to describe quantitatively our measurements of the stick phase duration. Such a model however fails to predict the full stick-slip cycle duration, revealing strong dynamical effects during the slip phase.
1. Introduction
Everyday examples of adhesive peeling are found in applications such as labels, stamps, tape rollers, self-adhesive envelopes or post-it notes. During the peeling of those adhesives, a dynamic instability of the fracture process corresponding to a jerky advance of the peeling front called “stick-slip” may occur. This stick-slip instability has been an industrial concern since the 1950's because it leads to noise levels above the limits set by work regulations, to adhesive layer damage and/or to mechanical problems on assembly lines. This instability is still a limiting factor for industrial productivity due to the limitations of generic technical solutions applied to suppress it, such as anti-adhesive silicon coating.From a fundamental point of view, the stick-slip instability of adhesive peeling is generally understood as the consequence of an anomalous decrease of the fracture energy Γ(νp) of the adhesive–substrate joint in a specific range of peeling front velocities νp.1–8 Indeed, when the peeling process also involves a compliance between the point where the peeling velocity is imposed and the fracture front, this decreasing fracture energy naturally leads to oscillations of the fracture velocity νp around the mean velocity V imposed by the operator. Often, it is simply the peeled ribbon elasticity which provides compliance to the system. From a microscopic perspective, such an anomalous decrease of the fracture energy Γ(νp) (correctly defined for stable peeling only) could correspond (but not necessarily) to the transition from cohesive to adhesive failure2,3 or between two different interfacial failure modes.4,7 More fundamentally, this decrease of the fracture energy has been proposed to be the consequence of the viscous dissipation in the adhesive material.9 De Gennes10 further pointed out the probable fundamental role of the adhesive material confinement (which was evidenced experimentally in ref. 3) in such viscoelastic theory. Since then, it has however appeared that a model based on linear viscoelasticity solely cannot be satisfactory and that the role of creep, large deformations and temperature gradient in the adhesive material is important (ref. 11–14 and references therein).
Experimentally, the stick-slip instability was first characterized thanks to peeling force measurements which revealed strong fluctuations in certain ranges of peeling velocity.1,3,5,6 Since then, it has also been studied through indirect measurements of the periodic marks left on the tape5,6,15,16 or of the emitted acoustic noise.17,18 Thanks to the progress in high speed imaging, it is now possible to directly access the peeling fracture dynamics in the stick-slip regime.19–21
In the late 1980's, Barquins and co-workers5,6 performed a series of peeling experiments of a commercial adhesive tape (3M Scotch® 602) at a constant pulling velocity V and for various lengths of peeled ribbon L. For the considered adhesive, the velocity range for which stick-slip was evidenced, thanks to peeling force fluctuation measurements, was shown to be 0.06 < V < 2.1 m s−1. In a sub-range of unstable peeling velocity 0.06 < V < 0.65 m s−1, the authors succeeded to access the stick-slip cycle duration thanks to the post-mortem detection of periodic marks left on the tape by stick-slip events. Moreover, they managed to model quantitatively the measured stick-slip period,5,6 assuming the fracture dynamics to remain a quasistatic problem during the stick phase and backing on measurements of the stable branch of the fracture energy Γ(νp) at low peeling velocities below the instability onset.
In this article, we revisit these experiments by studying the stick-slip dynamics during the peeling of a roller adhesive tape at an imposed velocity. The principal improvement compared to Barquins's seminal work is that, thanks to a high speed camera coupled to image processing, we are able to access the dynamics of the peeling fracture front. We focus on the study of the duration of the stick-slip cycle and its decomposition into stick and slip events, for which data are inaccessible through other techniques. We present experimental data of the stick and slip durations for a wide range of imposed peeling velocities V and for different peeled ribbon lengths L. We show that the model proposed by Barquins and co-workers5,6 describes the evolution of the duration of the stick phase, but fails to predict the duration of the whole stick-slip cycle due to unexpectedly long slip durations.
2. Experimental setup
In this section, we describe briefly the experimental setup which has already been presented in detail in a recent study.21 We peel an adhesive tape roller (3M Scotch® 600, made of a polyolefin blend backing coated with a layer of a synthetic acrylic adhesive, also studied in ref. 8, 19, and 21), mounted on a freely rotating pulley, by winding up the peeled ribbon extremity on a cylinder at a constant velocity V using a servo-controlled brushless motor (see Fig. 1). The experiments have been performed at a temperature of 23 ± 2° and a relative humidity of 45 ± 5%. The width of the tape is b = 19 mm, its thickness e = 38 μm and its Young's modulus E = 1.26 GPa. | ||
| Fig. 1 Schematic view of the experimental setup. The angles α and β are oriented clockwise and counterclockwise respectively. Roller diameter: 40 mm < 2R < 58 mm, roller and tape width: b = 19 mm. | ||
Each experiment consists of increasing the winding velocity from 0 up to the target velocity V. Once the velocity V is reached, it is maintained constant for two seconds before decelerating the velocity back to zero. When stick-slip is present this 2-second stationary regime of peeling provides sufficient statistics to compute well converged stick-slip mean features. We have varied the imposed velocity V from 0.0015 to 2.5 m s−1 for different values of the peeled tape length between L = 0.08 and 1.31 m. During the experiment, the peeled tape length L (Fig. 1) is submitted to variations, due to the stick-slip fluctuations and slow oscillations of the peeling point angular position, which however always remain negligible compared to its mean value (less than 0.3%).21
3. Peeling force measurement
Thanks to a force sensor (Interface® SML-5) on the holder maintaining the pulley, we are able to measure the mean value of the force F transmitted along the peeled tape during one experiment. When peeling is stable, we compute the strain energy release rate G from the mean value of the force F, following the traditional relationship for the peeling geometry22,23 | (1) |
In the context of elastic fracture mechanics, the condition for a fracture advance at a constant velocity νp is a balance between the release rate G and the fracture energy Γ(νp) required to peel a unit surface and accounting for the energy dissipation near the fracture front. When the fracture velocity νp approaches the Rayleigh wave velocity νR, Γ(νp) also takes into account the kinetic energy stored in material motions which leads to a divergence when νp → νR.24 In our system, the strain energy release rate G, computed through eqn (1), therefore stands as a measure of the fracture energy Γ(νp) when the peeling is stable only, i.e. when νp is constant. We will nevertheless compute G for the experiments in the stick-slip regime for which the peeling fracture velocity νp(t) is strongly fluctuating in time. In such a case, G cannot be used as a measure of the fracture energy: it is simply the time average of the peeling force F in units of G.
In Fig. 2, we plot G as a function of the imposed peeling velocity V for three different peeled tape lengths L. When the peeling is stable, the peeling force is nearly constant in time, whereas it fluctuates strongly when the stick-slip instability is present. The standard deviation of these fluctuations is represented in Fig. 2 with error bars. Large error bars are indicative of the presence of stick-slip.
 | ||
| Fig. 2 Mean value of the peeling force F, in units of the strain energy release rate G = F/b, as a function of V for 3 different peeled tape lengths L. Stars report the data of Barquins and Ciccotti8 for the same adhesive. The solid line is a power law fit G = 137V0.146 of the data in the low velocity stable branch. Error bars represent the standard deviation of the force fluctuations during one experiment. | ||
Between V = 0.0015 m s−1 and V = 0.10 ± 0.03 m s−1, we observe that G = F/b increases slowly with V and that its temporal fluctuations are nearly zero, revealing that the peeling is stable. This increasing branch G(V) is therefore a measure of the adhesive fracture energy Γ(νp = V) = G(V) for V < 0.10 ± 0.03 m s−1. Our results are compatible with the data reported by Barquins and Ciccotti8 for the same adhesive tape (see Fig. 2). However, they explored a much larger range of velocities in this stable branch of peeling, down to V = 10−5 m s−1. By using both series of measurements, it is reasonable to model the stable peeling branch with a power law, G(V) = aVn, with n = 0.146 and a = 137. For 0.10 ± 0.03 m s−1 < V ≤ 2.5 m s−1, we observe that the measured value of G(V) decreases with V. This tendency, which was already observed in previous experiments,25 is accompanied with the appearance of temporal fluctuations which are the trace of the stick-slip instability. From these data, we can estimate the onset of the instability to be Va = 0.10 ± 0.03 m s−1. The measured decreasing branch of G(V) for V > Va appears as a direct consequence of the anomalous decrease of the fracture energy at the origin of the instability. It is important to note that the measured mean value of G = F/b is nearly independent of the length of peeled ribbon L. This result is natural in the stable peeling regime but was a priori unknown in the stick-slip regime.
Barquins and Ciccotti8 succeeded to measure a second stable peeling branch for V ≥ 19 m s−1. This increasing branch constitutes a measure of the peeling fracture energy Γ(νp = V) = G(V) in a fast and stable peeling regime. In ref. 8, this branch is inferred to exist for velocities even lower than V = 19 m s−1, although it was not possible to measure it. Backing on the data of ref. 6 for a very close adhesive, one can however guess that the local minimum value of G(V), corresponding to a velocity in the range 2.5 m s−1 < V < 19 m s−1, would be bound by G0,1 = 18 < G < G0,2 = 33 J m−2.
4. Peeling point dynamics
The local dynamics of the peeling point is imaged using a high speed camera (Photron FASTCAM SA4) at a rate of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fps. The recording of each movie is triggered once the peeling has reached a constant average velocity V ensuring that only the stationary regime of the stick-slip is studied. Through direct image analysis,21 the movies allow access to the curvilinear position of the peeling point
000 fps. The recording of each movie is triggered once the peeling has reached a constant average velocity V ensuring that only the stationary regime of the stick-slip is studied. Through direct image analysis,21 the movies allow access to the curvilinear position of the peeling point ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) α(t) = Rα in the laboratory frame (with α being the angular position of the peeling point and R being the roller diameter, α > 0 in Fig. 1). Image correlations on the adhesive tape roller contrast pattern further allow direct access to its angular velocity dβ/dt in the laboratory frame (where β is the unwrapped angular position of the roller, β > 0 in Fig. 1,
α(t) = Rα in the laboratory frame (with α being the angular position of the peeling point and R being the roller diameter, α > 0 in Fig. 1). Image correlations on the adhesive tape roller contrast pattern further allow direct access to its angular velocity dβ/dt in the laboratory frame (where β is the unwrapped angular position of the roller, β > 0 in Fig. 1, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) β(t) = Rβ). We finally compute numerically the curvilinear position
β(t) = Rβ). We finally compute numerically the curvilinear position ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p(t) =
p(t) = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) β(t) +
β(t) + ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) α(t) and velocity νp(t) = d
α(t) and velocity νp(t) = d![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p/dt of the peeling point in the roller reference frame.
p/dt of the peeling point in the roller reference frame.
The curvilinear position of the peeling point ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) α(t) in the laboratory frame is actually estimated from the position of the peeled ribbon at a small distance of 0.30 ± 0.05 mm from the peeling fracture front on the roller surface. We therefore do not detect strictly the peeling fracture front position but a very close quantity only. This procedure can consequently introduce some bias in our final estimation of the fracture front velocity νp(t). This bias is notably caused by the changes in the radius of curvature of the tape at the junction with the substrate which are due to the force oscillations in the peeled tape characteristics of the stick-slip instability. Such an effect actually biases the measurement toward larger velocities during the stick phase and lower velocities during the slip phase. Another effect that leads to uncertainties in velocity measurement is the emission of a transverse wave in the peeled tape when the fracture velocity abruptly changes at the beginning and at the end of slip phases.
α(t) in the laboratory frame is actually estimated from the position of the peeled ribbon at a small distance of 0.30 ± 0.05 mm from the peeling fracture front on the roller surface. We therefore do not detect strictly the peeling fracture front position but a very close quantity only. This procedure can consequently introduce some bias in our final estimation of the fracture front velocity νp(t). This bias is notably caused by the changes in the radius of curvature of the tape at the junction with the substrate which are due to the force oscillations in the peeled tape characteristics of the stick-slip instability. Such an effect actually biases the measurement toward larger velocities during the stick phase and lower velocities during the slip phase. Another effect that leads to uncertainties in velocity measurement is the emission of a transverse wave in the peeled tape when the fracture velocity abruptly changes at the beginning and at the end of slip phases.
Fig. 3(a) and (c) represent the fracture position ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p(t) and velocity νp(t) as a function of time for a typical experiment performed at V = 0.55 m s−1 and L = 0.47 m. In these figures, we observe alternate phases of slow (stick phase) and fast (slip phase) peeling which are the signatures of the stick-slip motion. These large velocity fluctuations are quite regular in terms of duration and to a lesser extent in terms of amplitude at least at the considered peeling velocity. Our general data analysis further consists of the decomposition of the signal of instantaneous peeling velocity νp(t) into stick-slip cycles by setting the beginning of each cycle at times tn (n denoting the nth cycle) when νp(tn) = V and dνp(tn)/dt < 0. From these data, we extract the duration Tss of each stick-slip cycle for which we define a rescaled time t′ = (t − tn)/Tss. We further compute the phase averaged evolution of the peeling fracture velocity νp(t′) from t′ = 0 to 1 considering all the stick-slip cycles in one experiment. With this procedure, we finally extract for each peeling velocity V and peeled tape length L the typical fracture velocity evolution during a stick-slip cycle getting rid of intrinsic fluctuations of the stick-slip period. In Fig. 3(b) and (d), we show the phase averaged position and velocity profiles, corresponding to Fig. 3(a) and (c) respectively, as a function of t = t′〈Tss〉 (〈〉 denotes the ensemble averaged value over all the cycles in one experiment).
p(t) and velocity νp(t) as a function of time for a typical experiment performed at V = 0.55 m s−1 and L = 0.47 m. In these figures, we observe alternate phases of slow (stick phase) and fast (slip phase) peeling which are the signatures of the stick-slip motion. These large velocity fluctuations are quite regular in terms of duration and to a lesser extent in terms of amplitude at least at the considered peeling velocity. Our general data analysis further consists of the decomposition of the signal of instantaneous peeling velocity νp(t) into stick-slip cycles by setting the beginning of each cycle at times tn (n denoting the nth cycle) when νp(tn) = V and dνp(tn)/dt < 0. From these data, we extract the duration Tss of each stick-slip cycle for which we define a rescaled time t′ = (t − tn)/Tss. We further compute the phase averaged evolution of the peeling fracture velocity νp(t′) from t′ = 0 to 1 considering all the stick-slip cycles in one experiment. With this procedure, we finally extract for each peeling velocity V and peeled tape length L the typical fracture velocity evolution during a stick-slip cycle getting rid of intrinsic fluctuations of the stick-slip period. In Fig. 3(b) and (d), we show the phase averaged position and velocity profiles, corresponding to Fig. 3(a) and (c) respectively, as a function of t = t′〈Tss〉 (〈〉 denotes the ensemble averaged value over all the cycles in one experiment).
From these phase averaged velocity profiles, we define, for each experimental condition V and L, stick events as continuous periods during which νp(t) < 3Va and slip events as continuous periods during which νp(t) > 3Va. According to the model of Barquins et al.5,6 a natural threshold in order to separate the stick and slip phases is the onset of the instability Va (as defined in Fig. 2). However, as discussed previously, due to the procedure used for the detection of the peeling point, our measurement of the fracture velocity can be affected by biases caused by the variation of the tape curvature at the peeling point and by the propagation of transverse waves in the tape. The effect of the latter can be observed in Fig. 3(d) in the early stage of the stick phase. In order to avoid taking into account the velocity biases in the decomposition of the stick-slip cycle, we chose for the threshold separating the stick and slip phases a value little larger than the “theoretical” threshold Va, that is to say 3Va.
Finally, as we have shown recently in ref. 21, when the peeling velocity V is increased, low frequency pendular oscillations of the peeling angle θ develop. Due to the dependence of the stick-slip instability onset on the mean peeling angle, these oscillations lead to intermittence in the stick-slip dynamics for peeling velocities V > 1.5 m s−1. We therefore exclude the experiments with V > 1.5 m s−1in the sequel. For the studied experiments, we have a mean peeling angle 〈θ〉 = 90 ± 3° with slow temporal variations in the range Δθ = ±15° during one experiment.
5. Stick-slip cycle duration
From the signal of peeling point position![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p(t) (see Fig. 3(a)), we define the stick-slip amplitude Ass as the distance travelled by the fracture during a stick-slip cycle. In Fig. 4, we report this amplitude Ass for each stick-slip event as a function of the corresponding stick-slip period Tss, for all events in 6 different experiments. These data gather close to the curve Ass = VTss. The large spread of the data along the curve Ass = VTss reflects the statistics of the stick-slip cycle amplitude and duration which could be due for instance to adhesive heterogeneities. In contrast, the dispersion of the data around the curve Ass = VTss is much smaller. It actually estimates the discrepancy between the imposed velocity V and the averaged fracture velocity for each stick-slip cycle. The observed small discrepancy actually traces back both measurement errors in the instantaneous fracture velocity and intrinsic fluctuations of the dynamics.
p(t) (see Fig. 3(a)), we define the stick-slip amplitude Ass as the distance travelled by the fracture during a stick-slip cycle. In Fig. 4, we report this amplitude Ass for each stick-slip event as a function of the corresponding stick-slip period Tss, for all events in 6 different experiments. These data gather close to the curve Ass = VTss. The large spread of the data along the curve Ass = VTss reflects the statistics of the stick-slip cycle amplitude and duration which could be due for instance to adhesive heterogeneities. In contrast, the dispersion of the data around the curve Ass = VTss is much smaller. It actually estimates the discrepancy between the imposed velocity V and the averaged fracture velocity for each stick-slip cycle. The observed small discrepancy actually traces back both measurement errors in the instantaneous fracture velocity and intrinsic fluctuations of the dynamics.
In Fig. 4, one can already see that the statistically averaged values of Ass and Tss increase with L for a given peeling velocity V. In the following, we will focus on the study of the statistical average 〈Tss〉 of the duration of the stick-slip oscillation and its decomposition into stick and slip phases with in mind the aim of testing the description of Barquins, Maugis and co-workers.5,6 There is no need to study the averaged stick-slip amplitude 〈Ass〉 since it is unequivocally related to 〈Tss〉 through 〈Ass〉 = V 〈Tss〉.
In Fig. 5(a), we plot the mean stick-slip duration Tss as a function of V for three different lengths L of the peeled ribbon. The data correspond to the average 〈Tss〉 and the error bars correspond to the standard deviation of the statistics of Tss over all the stick-slip events in each experiment. In the following, since we will consider the averaged values only, we will skip the brackets 〈〉. At first sight, it appears that, within the error bars, the stick-slip duration Tss is stable over the major part of the explored range of peeling velocity V. One can however note that, independently of L, Tss tends to decrease with V for V ≤ Vc = 0.6 ± 0.1 m s−1. Such behavior is compatible with the observations of Barquins et al.5 but appears here over a rather limited velocity range. The characteristic velocity Vc = 0.6 ± 0.1 m s−1 above which Tss is nearly constant seems not to depend strongly on the length of the peeled ribbon L.
In Fig. 5(b), we show the mean durations of stick and slip events, Tstick and Tslip respectively, as a function of the imposed peeling velocity V for the experiments performed with the peeled length L = 0.47 m. Interestingly, we observe that the stick and slip phases evolve differently with V: the stick duration decreases with V, while the slip duration increases over the whole explored range of V. In consequence, the ratio Tstick/Tslip, presented in Fig. 6, decreases with V from Tstick/Tslip ∼ 4 ± 1 down to Tstick/Tslip ∼ 0.3 ± 0.2. Such behavior of Tstick/Tslip appears to be very little dependent on L according to Fig. 6. For V ≥ 0.90 ± 0.05 m s−1, Tstick/Tslip becomes smaller than 1, meaning that the slip phase is longer than the stick one. Our data therefore show that it is not possible to neglect the slip duration compared to the stick duration in general.
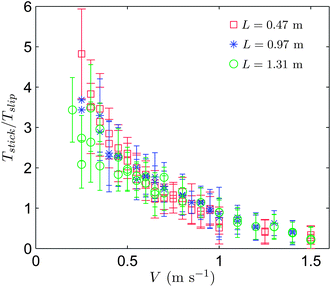 | ||
| Fig. 6 T stick/Tslipvs. V for 3 different L. Each data point corresponds to the average and each error bar to the standard deviation of the statistics over one experiment. | ||
6. Model
In this section, we compare our experimental data with the model proposed by Barquins, Maugis and co-workers in ref. 5 and 6. This model is based on measurements of the stable branch of the fracture energy Γ(νp) for low peeling velocities below the instability onset Va, and on the following assumptions:• During the stick phase, the equilibrium between the instantaneous energy release rate G = F/b and the fracture energy Γ(νp) (of the low velocity stable branch) is still valid dynamically, i.e. G(t) = Γ(νp(t)).
• The peeled ribbon remains fully stretched during the peeling, which means
 | (2) |
• The slip duration is negligible compared to the stick duration.
Backing on these hypotheses, it is possible to derive a prediction for the stick-slip duration Tss. Introducing the inverted function νp = Γ−1(G) and noting that du/dt = V − νp (see the next paragraph and ref. 21), eqn (2) leads to the dynamical relationship
 | (3) |
 | (4) |
In this model, the ribbon is assumed to remain taut during the whole stick-slip cycle. In order to challenge the validity of this hypothesis, let us estimate the evolution of the elongation u(t) of the tape as a function of time. If we note P(t) the peeling point position and M the point where the peeled tape is wound, we can define the quantity u(t) as the difference between the distance  and the length of the peeled tape in the unstrained state. If u(t) is positive, this quantity indeed measures the elongation of the tape as in eqn (2), whereas it measures the excess of slack tape if it is negative. Following ref. 21, one can show that
and the length of the peeled tape in the unstrained state. If u(t) is positive, this quantity indeed measures the elongation of the tape as in eqn (2), whereas it measures the excess of slack tape if it is negative. Following ref. 21, one can show that
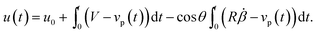 | (5) |
 . The elongation/slack u(t) increases with
. The elongation/slack u(t) increases with  during the stick phase and decreases with the same amplitude
during the stick phase and decreases with the same amplitude  during the slip phase. This compensation is ensured by the fact that the averaged velocity over the stick-slip cycle matches the imposed velocity V, i.e.
during the slip phase. This compensation is ensured by the fact that the averaged velocity over the stick-slip cycle matches the imposed velocity V, i.e. , and is valid whether or not the tape remains always taut during the stick-slip cycle.
, and is valid whether or not the tape remains always taut during the stick-slip cycle.
To test the relevance of the hypothesis of a tape always in tension, one can actually compare the increase/decrease Δu of the quantity u(t) during the stick/slip phase with the one predicted by the quasistatic model of Barquins and co-workers
 | (6) |
An equivalent but more instructive way to test the model of Barquins and co-workers is to integrate numerically eqn (4) and compare it with experimental measurements of the stick duration. To do so, we use the fit of the data of the energy release rate G(V) in Fig. 2, i.e. G(V) = Γslow(V) = aVn, with n = 0.146 and a = 137. The value of G0 is affected by a significant uncertainty in our data. We will therefore use two different guesses corresponding to the limit values introduced in page 3 (see G0,1 and G0,2 in Fig. 2). These values of G0 correspond to two limit values of the fracture velocity at the beginning of the stick phase: V0,1 = 10−6 m s−1 measured in another adhesive but with a close behavior,6 and V0,2 = 6.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 m s−1 which is an upper limit for V0 according to the data of Fig. 2.
10−5 m s−1 which is an upper limit for V0 according to the data of Fig. 2.
In the inset of Fig. 7(b), we report the measured data for Tss/L as a function of V for three different lengths L as well as the predictions of eqn (4) with V0,1 (solid line) and V0,2 (dashed line). The model appears compatible with the experimental data only for a marginal range of very low peeling velocities. Once V > 0.5 m s−1, the measured values of Tss/L indeed deviate more and more from the theoretical prediction. A first natural explanation for this discrepancy is that the assumption of a negligible slip duration Tslip (barely verified for low velocities for which 0.25 < Tslip/Tstick < 0.5) becomes more and more false as V is increased (see Fig. 6).
 | ||
Fig. 7 (a) Tslip/L, (b) Tstick/L and Tss/L (insert) vs. V for 3 different L. Each data point corresponds to the average and each error bar to the standard deviation of the statistics over one experiment. In (a), the curve close to the x-axis represents the theoretical prediction for a quasistationary slip phase. In (b), the lines show the predictions of eqn (4) with Va = 0.10 m s−1 and V0,1 = 10−6 m s−1 (solid line) or V0,2 = 6.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 m s−1 (dashed line). 10−5 m s−1 (dashed line). | ||
In Fig. 7(b) we therefore directly plot Tstick/L as a function of V, along with the prediction (4). One can note that the theoretical predictions using the two limit guesses for V0 are not very different. A first interesting result is that the stick duration appears, to the first order, proportional to the peeled tape length L as evidenced by the reasonable collapse of the data Tstick/L on a master curve, which is compatible with the analytical prediction of the model (4). But more importantly, we observe that for the range of velocities explored, the model for Tstick, which does not use any adjustable parameter, reproduces very well the experimental data.
Obviously, one can consider an equivalent quasistationary approximation during the slip phase in order to predict the slip duration using Γfast−1(G) instead of Γslow−1(G) in eqn (4). Here, Γfast−1(G) corresponds to the inverse of the energy fracture G = Γfast(νp) in the fast and “stable” peeling regime of Fig. 2. The integration using the model of the fast branch Γfast(V) = 6.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5V4.5 (see Fig. 2) however leads to values of Tslip always 2 orders of magnitude smaller than the experimental values as evidenced in Fig. 7(a). It is however worth noting that the collapse of the data Tslip/L for the different L values shows that Tslip increases nearly linearly with L.
10−5V4.5 (see Fig. 2) however leads to values of Tslip always 2 orders of magnitude smaller than the experimental values as evidenced in Fig. 7(a). It is however worth noting that the collapse of the data Tslip/L for the different L values shows that Tslip increases nearly linearly with L.
7. Discussion
In this paper, we report experiments on a roller adhesive tape peeled at a constant velocity focusing on the regime of stick-slip instability. From fast imaging recordings, we extract the dependence of the stick and slip phase durations on the imposed peeling velocity V and peeled ribbon length L.The stick phase duration Tstick of the stick-slip oscillations is shown to be nearly proportional to the peeled tape length L and to decrease with the peeling velocity V. These data moreover appear in quantitative agreement with the predictions of a model proposed by Barquins, Maugis and co-workers in ref. 5 and 6 which do not introduce any adjustable parameter. This successful comparison confirms the relevance of the two main assumptions made in the model: (i) the tape remains in tension during the whole stick-slip cycle; (ii) the principle of an equilibrium between the instantaneous energy release rate G(t) = F(t)/b and the fracture energy Γ(νp(t)), as measured in the steady peeling regime, is valid dynamically during the stick phase.
Describing the peeling dynamics as a function of time t by the knowledge of the fracture velocity νp(t) and of the force F(t) = bG(t) in the peeled tape, the considered model further assumes that the system jumps instantaneously, at the end of the stick phase, from the “slow” stable branch to the “fast” stable branch of the steady fracture energy G = Γ(νp) and then instantaneously backward from the “fast” branch to the “slow” branch at the end of the slip phase. In such a framework, reproducing the assumptions (i) and (ii) for the slip phase leads to a prediction for the slip duration. We have shown that this prediction is at least hundred times smaller than the slip phase duration Tslip measured in our experiments. We actually report that in contrast to what is finally proposed in ref. 5 and 6, the slip duration Tslip cannot be neglected compared to the stick one Tstick, since it is at best 4 times smaller, and becomes even larger than Tstick for V ≥ 0.90 ± 0.05 m s−1.
These last experimental results account for the existence of strong dynamical effects during the slip phase which can therefore not be described by a quasistatic hypothesis. These dynamical effects could be due to the inertia of the ribbon close to the fracture front. Some models also predict a strong influence of the roller inertia.18,26 Notably, thanks to numerical computation, De and Ananthakrishna26 have shown that for certain values of the roller inertia, the slip phase could consist of several jumps from the “fast stable” branch to the “slow stable” branch in the (νp, G = Γ(νp)) diagram. Such a process would certainly produce a longer slip time than expected in the framework of Barquins's model. It would be most interesting to confront our experimental observations to the predictions of this model, based on a detailed set of dynamical equations and ad hoc assumptions made on the velocity dependence of Γ. However, such a comparison is not straightforward in our current setup since we do not have the temporal and spatial resolutions to detect such eventual fast oscillations. Besides, in order to obtain a quantitative comparison, measurement of the instantaneous peeling force F(t) is required but it remains a challenge.
Acknowledgements
This work was supported by the French ANR through Grant “STICKSLIP” no. 12-BS09-014. We thank Costantino Creton and Matteo Ciccotti for fruitful discussions and Matteo Ciccotti for sharing data with us.References
- J. L. Gardon, J. Appl. Polym. Sci., 1963, 7, 625–641 CrossRef CAS.
- A. N. Gent and R. P. Petrich, Proc. R. Soc. London, Ser. A, 1969, 310, 433–448 CrossRef.
- D. W. Aubrey, G. N. Welding and T. Wong, J. Appl. Polym. Sci., 1969, 13, 2193–2207 CrossRef CAS.
- D. W. Aubrey and M. Sherriff, J. Polym. Sci., 1980, 18, 2597–2606 CAS.
- M. Barquins, B. Khandani and D. Maugis, C. R. Acad. Sci., Ser. II: Mec., Phys., Chim., Sci. Terre Univers, 1986, 303, 1517–1519 Search PubMed.
- D. Maugis and M. Barquins, in Adhesion 12, ed. K. W. Allen, Elsevier ASP, London, 1988, pp. 205–222 Search PubMed.
- C. Derail, A. Allal, G. Marin and P. Tordjeman, J. Adhes., 1997, 61, 123–157 CrossRef CAS , 1998, 68, 203–228.
- M. Barquins and M. Ciccotti, Int. J. Adhes. Adhes., 1997, 17, 65–68 CrossRef CAS.
- D. Maugis, J. Mater. Sci., 1985, 20, 3041–3073 CrossRef CAS.
- P.-G. de Gennes, Langmuir, 1996, 12, 4497–4500 CrossRef CAS.
- A. N. Gent, Langmuir, 1996, 12, 4492–4496 CrossRef CAS.
- G. Carbone and B. N. J. Persson, Phys. Rev. Lett., 2005, 95, 114301 CrossRef CAS.
- E. Barthel and C. Fretigny, J. Phys. D: Appl. Phys., 2009, 42, 19 CrossRef.
- H. Tabuteau, S. Mora, M. Ciccotti, C.-Y. Hui and C. Ligoure, Soft Matter, 2011, 7, 9474–9483 RSC.
- J. L. Racich and J. A. Koutsky, J. Appl. Polym. Sci., 1975, 19, 1479–1482 CrossRef CAS.
- G. Ryschenkow and H. Arribart, J. Adhes., 1996, 58, 143–161 CrossRef CAS.
- M. Gandur, M. Kleinke and F. Galembeck, J. Adhes. Sci. Technol., 1997, 11, 11–28 CrossRef CAS PubMed.
- M. Ciccotti, B. Giorgini, D. Vallet and M. Barquins, Int. J. Adhes. Adhes., 2004, 24, 143–151 CrossRef CAS PubMed.
- P.-P. Cortet, M. Ciccotti and L. Vanel, J. Stat. Mech.: Theory Exp., 2007, P03005 CrossRef.
- S. T. Thoroddsen, H. D. Nguyen, K. Takehara and T. G. Etoth, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 046107 CrossRef CAS.
- P.-P. Cortet, M.-J. Dalbe, C. Guerra, C. Cohen, M. Ciccotti, S. Santucci and L. Vanel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022601 CrossRef.
- R. S. Rivlin, Paint Technol., 1944, 9, 215–216 Search PubMed.
- K. Kendall, J. Phys. D: Appl. Phys., 1975, 8, 1449–1452 CrossRef.
- L. B. Freund, Dynamic fracture mechanics, Cambridge University Press, London, 1998 Search PubMed.
- Y. Yamazaki and A. Toda, Physica D, 2006, 214, 120–131 CrossRef PubMed.
- R. De and G. Ananthakrishna, Eur. Phys. J. B, 2008, 61, 475–483 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |



