Multiple metal-bound oligomers from Ir-catalysed dehydropolymerisation of H₃B·NH₃ as probed by experiment and computation

Abstract

Multiple metal-bound oligomers in the dehydropolymerisation of H₃B·NH₃ have been observed by electrospray-ionisation mass spectrometry and NMR spectroscopy using the catalytic metal fragment {Ir(PCy₃)₂(H)₂}⁺. A computational study suggests that sterics dictate whether multiple dehydrogenation/B–N coupling of amine-boranes H₃B·NRR'H (R, R′ = Me or H) is observed, and also demonstrates the experimentally observed requirement for additional amine-borane to promote dehydrocoupling.

---

Introduction

The dehydropolymerisation of amine-boranes H₃B·NRH₂ (R = H, Me) is a promising methodology for the synthesis of new B–N materials, for example polymeric materials that are isoelectronic with societally ubiquitous polyolefins,^1,2 or precursors to B–N ceramics such as white graphene.³ Catalysis of these processes by a transition metal fragment offers potential for control of kinetics and final product distributions, and various systems have been shown to promote dehydropolymerisation.^4–12 Non-metal catalysed processes have also been discussed.^13,14

The mechanism of catalytic dehydropolymerisation of H₃B·NH₃ or H₃B·NMeH₂ has been suggested to be based upon dehydrogenation followed by a second metal-mediated coordination polymerisation step.^{6,9,10,12,15,16} In particular, there is growing evidence to suggest that transient amino-borane (e.g. H₂B=NH₂ or H₂B=NMeH), that arises from dehydrogenation of the precursor amine-borane, remains associated with the metal.¹⁷ If liberated these unsaturated fragments form the corresponding borazine by oligomerisation (Scheme 1), or can be trapped by hydroboration of exogenous cyclohexene – assuming such reactions are faster than polymerisation (i.e. B–N bond formation leading to a growing polymer chain). In addition bulky primary amine-boranes, H₃B·N^tBuH₂,¹⁸ or secondary amine-boranes, e.g. H₃B·NMe₂H,^19,20 give simple amino-borane products rather than extensive oligomerisation. Adding to the complexity, different metal/ligand combinations likely lead to subtly different mechanisms.^8,10,12

Scheme 1 Dehydrogenation and dehydropolymerisation of amine-boranes; full pathways not shown.

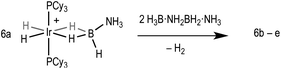
Direct mechanistic insight into the dehydropolymerisation process through the observation of intermediates has been sparse. Recently we reported the isolation of the product of the first oligomerisation event in such a process by reaction of [Ir(PCy₃)₂(H)₂(H₂)₂][BAr^F₄], 1, with 2 equivalents of H₃B·NMeH₂ to form [Ir(PCy₃)₂(H)₂(η²-H₃B·NMeHBH₂·NMeH₂)][BAr^F₄], 5b, (Scheme 2).²¹ This reaction is slow and does not produce higher oligomers, and a tentative mechanism was suggested to account for this selectivity. With bulkier H₃B·NMe₂H only dehydrogenation to form the bound amino-borane (i.e.4a*) is observed.¹⁹ We now report that with H₃B·NH₃ dehydropolymerisation can also be promoted by 1 and that, in contrast to H₃B·NMeH₂, higher oligomeric products bound to the metal centre (6a–e, Scheme 2) can be observed by electrospray ionisation mass spectrometry (ESI-MS) and NMR spectroscopy. ESI-MS provides the ideal analytical platform to study these processes as it allows for the convenient analysis of mixtures of products under inert conditions.^22,23 Computational studies^{10,19,24–27} offer a mechanistic rationale for oligomerisation that explains both the difference in the degree of oligomerisation with increasing steric bulk between the amine-boranes H₃B·NH₃, H₃B·NMeH₂ and H₃B·NMe₂H and the previously noted requirement for additional amine-borane to promote this process.²¹

Scheme 2 Selected examples of compounds discussed in this study. [Ir(PCy₃)₂(H)₂{η²-H₃B·(NRHBH₂)_n·NRH₂}][BAr^F₄], R = Me, 5; H, 6; n = 0, a; n = 1, b; n = 2, c; n = 3, d; n = 4, e. [BAr^F₄]⁻ anions are not shown. * = corresponding amino-borane.

Results and discussion

Addition of one equivalent of H₃B·NH₃ to 1¹⁹ in C₆H₅F solvent results in the immediate formation of the sigma amine-borane complex [Ir(PCy₃)₂(H)₂(η²-H₃B·NH₃)][BAr^F₄] 6a in quantitative yield by NMR spectroscopy. There is no onward dehydrogenation after 4 hours under these conditions, but addition of further H₃B·NH₃ (10 equivalents total) results in the formation of higher oligomers, [Ir(PCy₃)₂(H)₂{η²-H₃B·(NH₂BH₂)_n·NH₃}][BAr^F₄] n = 1–4. This requirement for additional amine-borane to promote dehydrogenation has been noted before in these systems, although its role has only been speculated upon.²¹Fig. 1 shows the ESI-MS spectra of the reaction of 1 with the amine-boranes H₃B·NMe_xH_3−x (x = 0–3) demonstrating the increasing degrees of dehydrogenation and oligomerisation with decreasing steric bulk of the amine-borane. Under these conditions H₃B·NMe₂H undergoes dehydrogenation with no subsequent B–N coupling (4a*),¹⁹ while H₃B·NMeH₂ gives the product of one dehydrocoupling event (5b).²¹ By contrast for H₃B·NH₃ metal-bound oligomers arising from up to four of these dehydrocoupling events are observed by ESI-MS (6b–e), which all show excellent fits with calculated isotopomer patterns, with 6d/e (n = 4, 5; Scheme 2) observed as [M–H₂]⁺ cations. In the ¹H{¹¹B} NMR spectrum of this mixture three distinct pairs of Ir⋯H–B and Ir–H environments are observed in an approximate 1 : 10 : 10 ratio (see ESI†), which are assigned to 6a, 6b and 6c respectively (vide infra), consistent with the major species observed by ESI-MS (6a–c). The ¹¹B{¹H} NMR spectrum of this mixture shows broad, potentially overlapping, signals in the Ir⋯H₃B and {BH₂} regions, and the ³¹P{¹H} NMR spectrum shows two tightly-coupled AB doublets in approximately equal ratio, the third species (i.e.6a) being too low in intensity to be observed. The identity of these complexes has been confirmed by the independent synthesis of 6b and 6c from the preformed borazanes H₃B·NH₂BH₂·NH₃²⁸ and H₃B·(NH₂BH₂)₂·NH₃²⁹ respectively. Scheme 3 shows the solid-state structure (as the [BAr^Cl₄]⁻ salts³⁰ from [Ir(PCy₃)₂(H)₂(H₂)₂][BAr^Cl₄], 2) of 6c, alongside that of 6a, which confirm formulation, being closely related to analogous complexes 3a, 4a, 5a and 5b.^19,21 Over time (24 h) these mixtures of products degrade to give bimetallic products identified by ESI-MS as [{Ir(PCy₃)₂(H)₂}₂{H₃B(NH₂BH₂)_nH}]⁺7a–d (n = 0 to 3 respectively), presumably in which the anionic amino-boranes [H₃B(NH₂BH₂)_nH]⁻²⁹ bridge between two cationic metal fragments. Recrystallisation of this mixture afforded small amounts of the borohydride complex³¹ [{Ir(PCy₃)₂(H)₂}₂(η²,η²-H₂BH₂)][BAr^F₄] 7a (see ESI† for a solid-state structure). We were unable to definitely characterise the other byproducts of this decomposition.

Fig. 1 ESI-MS (positive mode) of 1 (C₆H₅F solution) and 10 equivalents of: (A) H₃B·NMe₃, 3a; (B) H₃B·NMe₂H, 4a* (96 h, 3 equiv.); (C) H₃B·NMeH₂, 5a/5b (D) H₃B·NH₃, 6a–e; Calculated isotopomer m/z given in italics; n = 4 obs. m/z = 871.63 [M − H₂]⁺, calc. 871.62. After 4 hours unless otherwise stated. See Scheme 2 for numbering, and ESI† for an expansion of (D).

Scheme 3 Synthesis of 6a, 6b and 6c. Solid-state structures (50% displacement ellipsoids) of 6a and 6c. Selected hydrogen atoms are shown and the [BAr^Cl₄]⁻ anions are omitted for clarity. See ESI† for full details.

Borazine was also observed during the oligomerisation of H₃B·NH₃ (∼10% by ¹¹B NMR spectroscopy relative to [BAr^F₄]⁻), which might suggest free amino-borane is formed as a transient intermediate during the reaction.^15,18 Addition of excess cyclohexene to the reaction did not result in the observation of any hydroboration product, Cy₂B=NH₂, a trapping reaction that has previously been suggested to be indicative of free amino-borane in dehydrocoupling reactions.¹⁵ As recently noted, however, this process relies on hydroboration being kinetically competitive with oligomerisation, which might not necessarily be the case.¹⁰

Although these data are consistent with a growing oligomeric chain at the {Ir(PCy₃)₂(H)₂}⁺ fragment, similar to those observed by ESI-MS for olefin polymerisation,^32,33 these observations cannot discount a scenario where metal-catalysed dehydrogenation forms the free amino-borane, H₂B=NH₂, which then polymerises off-metal,¹³ with the most soluble short-chain oligomers then coordinating to the metal fragment. However, as computation suggests (vide infra) that the first dehydrogenation has a significantly higher barrier than subsequent oligomerisation we propose that this scenario is less likely. To probe further the oligomerisation process, three sequential additions of 1.1 equivalents of H₃B·NH₃ to 1 gave progressively longer oligomer chains (i.e.6a–6c) as measured by ESI-MS (see ESI†), although this mixture was biased towards 6a and 6b, suggesting that the sigma-bound oligomeric units, e.g.6b or 6c, are only weakly bound with the metal centre and can be displaced by excess H₃B·NH₃. Confirming this, addition of two equivalents of H₃B·NH₃ to 6c immediately results in a mixture of 6a–c and free H₃B·(NH₂BH₂)₂·NH₃, with 6c the major observed product. After 4 hours this has developed into a mixture of 6a–e with 6b and 6c the major products. Addition of 2 equivalents of H₃B·NH₂BH₂·NH₃ to 6a results in the formation of 6b and relatively smaller amounts of 6c–6e (by ESI-MS), the latter presumably derived from further dehydrocoupling events from 6b with H₃B·NH₃ (Scheme 4). Overall this suggests a mechanism in which the formed sigma-bound oligomer can be displaced by other amine-boranes, i.e. reversible chain transfer can occur. At the end of the reaction (24 h) a white solid is recovered that shows an IR spectrum essentially identical to polyaminoborane.³⁴ Use of 5 equivalents each of H₃B·NH₃ and H₃B·NMeH₂ gave a mixture of metal-bound co-oligomers [Ir(PCy₃)₂(H)₂{H(H₂BNH₂)_x(H₂BNMeH)_yH}]⁺ (x = 0, 1, y = 1, 2; x = 1, y = 0; x = 2, y = 1).

Scheme 4 Addition of 2 equivalents of H₃B·(NH₂BH₂)·NH₃ to 6a results in the formation of higher oligomers.

Density functional theory (DFT) calculations³⁵ have been used to study the mechanism of the dehydrocoupling of H₃B·NH₃ at 6a with particular focus on (i) the requirement for additional H₃B·NH₃ to induce dehydrogenation, (ii) the mechanism of the B–N coupling step and (iii) the varying affinities of the different amine-boranes toward oligomerisation. These calculations employed PMe₃ ligands, with [Ir(PMe₃)₂(H)₂(η²-H₃B·NMe_xH_3−x)]⁺ (denoted 6a′, x = 0, 5a′, x = 1 and 4a′, x = 2) the model initial reactants, and use a BP86-D3(C₆H₅F) protocol. We report free energies derived from gas-phase BP86-optimisations, corrected for dispersion and solvation effects. Each key step in the dehydrocoupling process (B–H/N–H bond activation and B–N bond coupling) presented more than one possible transition state and the most accessible of these are presented here, with alternative structures given in the ESI.†

We have previously modelled the dehydrogenation of H₃B·NMe₂H in [Ir(PMe₃)₂(H)₂(η²-H₃B·NMe₂H)]⁺ (4a′) to form the corresponding amino-borane adduct (i.e.4a′*, a model of 4a* in Scheme 2) and defined a mechanism based on sequential B–H activation, H₂ loss and rate-limiting N–H activation.¹⁹ Applying this mechanism to H₃B·NH₃ dehydrogenation in 6a′ reveals a barrier of 33.8 kcal mol⁻¹ in which the N–H activation step is again rate-limiting (see Fig. S1–3, ESI†). With an added H₃B·NH₃ molecule a related mechanism can be characterised but with a significantly reduced barrier of 26.7 kcal mol⁻¹ (Fig. 2). In this process the second H₃B·NH₃ molecule first adds to 6a′ to give [Ir(PMe₃)₂(H)₂(η¹-H₃B·NH₃)₂]⁺, I6a′₁, with a binding energy of 5.0 kcal mol⁻¹. This stabilisation is in part due to a BH(δ⁻)⋯H(δ⁺)N dihydrogen interaction between the two H₃B·NH₃ ligands.^36,37 B–H activation in I6a′₁ entails a barrier of 16.6 kcal mol⁻¹viaTS6a′_BH1 and proceeds with concomitant reductive coupling of the two hydride ligands to give [Ir(PMe₃)₂(BH₂NH₃)(H)(H₂)(η¹-H₃B·NH₃)]⁺, I6a′₂ (G = +15.9 kcal mol⁻¹). H₂ loss then leads to I6a′₃ (G = +10.7 kcal mol⁻¹) from which rate-limiting N–H activation occurs viaTS6a′_NH1 (G = +26.7 kcal mol⁻¹) to give I6a′₄ in which both an amine- and an amino-borane are bound to the metal centre.

Fig. 2 Computed free energy reaction profile (kcal mol⁻¹, BP86-D3(C₆H₅F)) for dehydrogenation of H₃B·NH₃ in 6a′ in the presence of added H₃B·NH₃.

The computed geometry of TS6a′_NH1 is shown in Fig. 3a and shows transfer of H¹⁴ from the BH₂NH₃ ligand to Ir (N¹⋯H¹⁴ = 1.42 Å; Ir⋯H¹⁴ = 1.74 Å) while a dihydrogen bonding interaction is maintained with the spectator H₃B·NH₃ ligand (H²⁴⋯H¹³ = 1.80 Å). This feature stabilises both TS6a′_NH1 and its precursor I6a′₃ and so contributes to a reduction in the overall barrier to dehydrogenation of 7.1 kcal mol⁻¹ compared to the reaction direct from 6a′ without added amine-borane. An alternative transition state, TS6a′_NH1(Alt 1), in which the second H₃B·NH₃ ligand adopts an η²-(B,H) bonding mode (similar to the amino-borane ligand in TS6a′_NH2, see Fig. 3b and below) is comparable in energy (G = +26.9 kcal mol⁻¹, see Fig. S6(b)†). Both forms of TS6a′_NH1 are consistent with dehydrogenation being facilitated by the addition of amine-borane to 6a′. Similar reductions in barriers to dehydrogenation have very recently been reported for H₃B·NMe₂H dehydrogenation using {Rh(chelating phosphine)}⁺ fragments.³⁸

Fig. 3 Computed structures of the rate-limiting N–H activation transition states of (a) a first and (b) a second H₃B·NH₃ molecule at 6a′. Key distances are in Å and PMe₃ H atoms are omitted for clarity.

For the subsequent B–N coupling step a total seven different pathways have been characterised. Four of these stem from intermediate I6a′₄ and entail B–H activation in the H₃B·NH₃ ligand to produce a Lewis acidic {H₂BNH₃} moiety that then couples with H₂B=NH₂. In most cases these processes occur in one step. Two further pathways have been characterised for the direct reaction of free H₂B=NH₂ with either 6a′ or its B–H activated form. All of these pathways, however, have computed barriers in excess of 28 kcal mol⁻¹, and as this is higher than the barrier to dehydrogenation these pathways would be inconsistent with the lack of any bound amino-borane intermediates being observed experimentally. Full details of these alternative pathways are given in the ESI (see Fig. S12†).

A significantly more accessible B–N coupling route was characterised that involved the direct reaction of two H₂B=NH₂ units. This process therefore requires the prior dehydrogenation of a second H₃B·NH₃ molecule and a pathway for this, analogous to that shown in Fig. 2, has been defined starting from I6a′₄ and forming [Ir(PMe₃)₂(H)₂(η²-H₂B=NH₂)]⁺ (I6a′₇) and free H₂B=NH₂ (see also Fig. S7–9†). I6a′₇ is closely related to that calculated for the product of dehydrogenation of H₃B·NMe₂H by the same fragment.¹⁹ The key N–H activation transition state in this process, TS6a′_NH2 (Fig. 3b), has a free energy of +24.2 kcal mol⁻¹ and features a spectator η²(B,H)–H₂B=NH₂ ligand³⁹ that stabilises the metal centre. Oligomerisation then proceeds through the reaction of I6a′₇ with H₂B=NH₂ and the associated reaction profile (Fig. 4) shows B–N coupling viaTS6a′_BN at only +17.9 kcal mol⁻¹. The structure of this transition state (Fig. 5) shows that the Ir-bound amino-borane has rearranged to an η²-(B,H) mode that exposes the pendant {NH₂} moiety to attack by the second, incoming amino-borane (N¹⋯B² = 2.37 Å). As this occurs a hydride transfers from Ir onto N² (Ir–H²⁴ = 1.63 Å; H²⁴⋯N² = 1.64 Å) to generate an η²-(B,H)–H₂B·NH₂BH₂·NH₃ ligand in the resultant intermediate I6a′₈ (G = +1.6 kcal mol⁻¹). Addition of H₂ (I6a′₉, G = +7.3 kcal mol⁻¹) and facile B–H reductive coupling gives the final model product, [Ir(PMe₃)₂(H)₂(η²-H₃B·NH₂BH₂·NH₃)]⁺, 6b′ (G = −10.9 kcal mol⁻¹).⁴⁰ This coupling process is similar to that suggested by Schneider and co-workers in bifunctional Ru(H)₂(PMe₃)(PNP) catalysis [PNP = HN(CH₂CH₂P^tBu₂)₂], in which an N–H activated H₃B·NH₃ group undergoes B–N coupling with H₂B=NH₂ during dehydropolymerisation.¹⁰

Fig. 4 Computed free energy reaction profile (kcal mol⁻¹, BP86-D3(C₆H₅F)) for B–N coupling and formation of oligomerisation product 6b′.

Fig. 5 Computed B–N coupling transition state with key distances in Å and PMe₃ H atoms omitted for clarity.

Reaction profiles analogous to those in Fig. 2 and 4 were also computed for the dehydrocoupling of H₃B·NMeH₂ at 5a′ and H₃B·NMe₂H at 4a′. Similar dehydrogenation barriers are found in each case (5a′/H₃B·NMeH₂: 25.2 kcal mol⁻¹; 4a′/H₃B·NMe₂H: 26.2 kcal mol⁻¹) and in the absence of a second amine-borane molecule these barriers increase to above 33 kcal mol⁻¹, reiterating the promotional effect of added amine-borane on this process. In contrast the B–N coupling transition states are more substrate-dependent and increase significantly in energy with the size of the amine-borane (6a′/H₃B·NH₃: 17.9 kcal mol⁻¹; 5a′/H₃B·NMeH₂: 19.9 kcal mol⁻¹; 4a′/H₃B·NMe₂H: 26.5 kcal mol⁻¹). This trend is consistent with oligomerisation being accessible for both H₃B·NH₃ and H₃B·NMeH₂, but this step becoming significantly more difficult for the larger H₃B·NMe₂H. Indeed oligomerisation is not seen experimentally for 4a/H₃B·NMe₂H under the conditions used here.⁴¹

An analogous mechanism based on dehydrocoupling of H₃B·NH₃ and H₃B·NH₂BH₂·NH₃ can account for the formation of the H₃B·(NH₂BH₂)₂·NH₃ trimer seen in 6c (modelled by 6c′). The key energetics are similar to those computed in the pathway for the formation of 6b′: dehydrogenation of H₃B·NH₃ (in the presence of H₃B·NH₂BH₂·NH₃) has an overall barrier of 26.3 kcal mol⁻¹, then dehydrogenation of H₃B·NH₂BH₂·NH₃ (now in the presence of H₂N=BH₂) has a barrier of 24.3 kcal mol⁻¹. The order of dehydrogenation is important, however, as the alternative initial dehydrogenation of H₃B·NH₂BH₂·NH₃ (in the presence of H₃B·NH₃) has a higher barrier of 28.1 kcal mol⁻¹ (see Fig. S15†). The subsequent B–N coupling transition state is again more accessible than dehydrogenation, TS6b′_BNa (Fig. 6a) having a computed energy of 21.2 kcal mol⁻¹. In this case there are two possible B–N coupling outcomes, depending on whether H₂B=NH₂ (as in TS6b′_BNa) or H₂B=NHBH₂·NH₃ (TS6b′_BNb, Fig. 6b) is bound to Ir in the transition state. The former case leads to a straight chain oligomer product, and is 2.3 kcal mol⁻¹ more stable than the alternative that gives a branched chain product. The barrier for this second oligomerisation step is close to that for the B–N coupling of H₃B·NMeH₂ (19.9 kcal mol⁻¹), highlighting the similar behaviour of these two mono-substituted amine-boranes. This in turn suggests that subsequent chain growth with further H₃B·NH₃ may proceed via transition states related to TS6b′_BNa in which the growing oligomer chain extends away from the metal centre with minimal additional steric impact. By the same token, H₃B·NMeH₂ trimerisation is more difficult with the equivalent transition state, TS5b′_BNa, equating to a higher barrier of +24.8 kcal mol⁻¹ (Fig. 6c). This trend towards higher oligomerisation barriers as the size of the amine-borane increases is consistent with the experimental observations (i.e.5a giving 5b alone whereas 6a can undergo multiple oligomerisation steps to give 6b–e).

Fig. 6 Transition states for B–N bond coupling leading to (a) straight chain and (b) branched chain formation in 6c′ as well as (c) straight chain formation in 5c′. Free energies (kcal mol⁻¹, BP86-D3(C₆H₅F)) are quoted relative to [Ir(PMe₃)₂(H)₂(η¹-H₃B·NMe_xH_3−x)(η¹-H₃B·NMe_xH_2−xBH₂·NMe_xH_3−x)]⁺ (I6b′₁, x = 0; I5b′₁, x = 1) as appropriate.

A potential side reaction within this mechanistic picture involves the cyclisation of two aminoborane fragments, either directly at the metal (e.g. via reaction of H₂B=NH₂ with [Ir(PMe₃)₂(H)₂(η²-H₂B=NH₂)]⁺, I6a′₇) or via an off-metal process^13,42 involving two free aminoboranes. In fact for H₃B·NH₃ both these processes are computed to be competitive with B–N coupling viaTS6a′_BN, dimerisation at I6a′₇ having a transition state energy of +15.4 kcal mol⁻¹ while the off-metal process has a barrier of 16.2 kcal mol⁻¹ (see Fig. S16†). Some dimerisation (and trimerisation) may therefore be anticipated, and indeed evidence of this is seen in the small amount of borazine that is observed as minor products in the oligomerisation processes.

Overall the proposed dehydrogenation/oligomerisation mechanism captures the key trends observed experimentally by ESI-MS and NMR spectroscopy. In particular the promotional effect of added amine-borane on dehydrogenation for all three H₃B·NMe_xH_3−x (x = 0–2) species and the decreasing propensity toward oligomerisation as the size of the amine-borane increases are reproduced. However, some issues do remain: (i) the absolute barriers computed for the dehydrogenation are ca. 26 kcal mol⁻¹ and so are rather high for a (albeit slow) room temperature process; (ii) once dehydrogenation has occurred, the competing H₂B=NH₂ dimerisation processes are computed to be slightly more favourable than oligomerisation. One reason for these discrepancies may be the use of a model system in the present study, where PMe₃ is used in place of PCy₃ ligands. However, an additional factor may be that both the key N–H activation (e.g.TS6a′_NH1) and B–N coupling (e.g.TS6a′_BN) transition states exhibit a vacant site that offers the potential for further stabilisation. Indeed a third H₃B·NH₃ molecule was found to promote both of these steps (see Scheme 5 and Fig. 7). Starting from I6a′₁.AB dehydrogenation proceeds with a reduced overall barrier of 22.4 kcal mol⁻¹ to give I6a′₇.AB at −4.9 kcal mol⁻¹ and from here B–N coupling has a barrier of only 9.4 kcal mol⁻¹. Moreover, B–N coupling (and the completion of the oligomerisation process) are now kinetically preferred over dimer formation. Therefore several substrate molecules may cooperate to promote the oligomerisation process. Alternatively a solvent molecule may interact with the unsaturated metal centre and so promote the oligomerisation step, although we have not attempted to explicitly model this here.

Scheme 5 Key steps in the oligomerisation of H₃B·NH₃ at I6a′₁ in the presence of a third H₃B·NH₃. Free energies (kcal mol⁻¹, BP86-D3(C₆H₅F)) are in kcal mol⁻¹.

Fig. 7 Computed B–N coupling transition state in the presence of a third H₃B·NH₃ molecule. Key distances in Å and PMe₃ H atoms omitted for clarity.

Conclusions

In summary, we report the observation and characterisation of multiple metal-bound oligomers in the dehydrocoupling of H₃B·NH₃. This contrasts with only a single oligomerisation event being observed for H₃B·NMeH₂ and none for H₃B·NMe₂H. Interrogation of the likely mechanism using computational methods reveals that initial dehydrogenation of H₃B·NH₃ is a higher energy process than both the subsequent dehydrogenation of a second amine-borane and metal-promoted B–N bond formation to form an oligomeric borazane bound to the metal centre. Steric factors play an important role in determining the barrier to B–N coupling which increases with x in the H₃B·NMe_xH_3−x series (x = 0–2). These studies also suggest a role for additional amine- or amino-borane in promoting dehydrocoupling processes through the formation of adduct species and complementary N–H⋯H–B interactions, an observation we noted from experimental studies both here and previously²¹ and recently from computational studies on related systems.⁴³

An overall mechanism that captures these observations is shown in Scheme 6. For H₃B·NH₃ initial dehydrogenation of the amine-borane (step 1) has the highest barrier (+26.7 kcal mol⁻¹), with the subsequent dehydrogenation of a second amine-borane (step 2) proceeding through a slightly lower energy transition state at +24.2 kcal mol⁻¹. The transition state for the B–N coupling of the resultant amino-boranes (step 3) is then most accessible of all (+17.9 kcal mol⁻¹). The rather high barrier to dehydrogenation (step 1) means that these systems turnover rather slowly, especially compared to others that rapidly promote dehydropolymerisation.^6–12 However, the corollary is that intermediates such as 6a–e can be observed, allowing for direct mechanistic insight. For subsequent oligomerisations (e.g. to form 6c, R = BH₂NH₃Scheme 6) the key transition state energies retain the same pattern, thus promoting formation of a growing oligomeric chain at the metal centre. When the amine-borane is changed to H₃B·NMeH₂ the same computed pattern still holds for the initial oligomerisation, but the second B–N coupling transition state (+24.8 kcal mol⁻¹) does becomes very close in energy to those for the two dehydrogenation steps (+25.4 kcal mol⁻¹ and +24.0 kcal mol⁻¹). Clearly B–N coupling is disfavoured by the greater bulk and experimentally only 5b is observed to be formed. For H₃B·NMe₂H no B–N bond formation to give a linear diborazane is observed under these experimental conditions, with 4a* formed only.

Scheme 6 Overall mechanism for the dehydrogenation and B–N bond forming events for H₃B·NH₃. R = H (first oligomerisation, i.e. to form 6b); R = BH₂NH₂ (second oligomerisation, 6c). Numbers on parenthesis are calculated barriers for the model system (kcal mol⁻¹). [Ir] = {Ir(PR₃)₂}⁺ (R = Cy, experiment; R = Me, computation).

B–N coupling is also calculated to be competitive with amino-borane cyclisation, consistent with the observation of a small amount of borazine. However, coupling must be faster than reaction of exogenous cyclohexene with amino-borane as no hydroborated product is observed under these conditions. Our mechanism therefore has some similarities to those recently proposed for the catalytic dehydropolymerisation of H₃B·NH₃ using a bifunctional Ru-based catalyst¹⁰ and of H₃B·NMeH₂ using Ir(^tBuPOCOP^tBu)H₂.^6,12 Although the intimate mechanistic details of these two systems likely differ, both propose dehydrogenation to form an amino-borane, that then must undergo fast metal-mediated B–N coupling, as neither system promotes hydroboration when exogenous cyclohexene is added.

Amine-borane dehydrocoupling presents a high degree of mechanistic complexity that is additionally highly catalyst specific. Although the precise mechanism outlined here might be rather system specific, the observations and suggested pathways presented might help guide future work on developing and understanding this challenging transformation. Ultimately the goal is the design of improved catalysts for this important process that have the potential to produce B–N materials “to order”.

Acknowledgements

The Rhodes Trust (A.K.), the University of Oxford, EPSRC (EP/J02127X/1) and the Spanish government (A.G.A.) for a Postdoctoral Fellowship (EX2009-0398).

Notes and references

1. E. M. Leitao, T. Jurca and I. Manners, Nat. Chem., 2013, 5, 817–829.
2. A. Staubitz, A. P. M. Robertson, M. E. Sloan and I. Manners, Chem. Rev., 2010, 110, 4023–4078.
3. Z. Liu, L. Song, S. Zhao, J. Huang, L. Ma, J. Zhang, J. Lou and P. M. Ajayan, Nano Lett., 2011, 11, 2032–2037.
4. B. L. Dietrich, K. I. Goldberg, D. M. Heinekey, T. Autrey and J. C. Linehan, Inorg. Chem., 2008, 47, 8583–8585.
5. A. Staubitz, A. Presa Soto and I. Manners, Angew. Chem., Int. Ed., 2008, 47, 6212–6215.
6. A. Staubitz, M. E. Sloan, A. P. M. Robertson, A. Friedrich, S. Schneider, P. J. Gates, J. S. auf der Günne and I. Manners, J. Am. Chem. Soc., 2010, 132, 13332–13345.
7. R. Dallanegra, A. P. M. Robertson, A. B. Chaplin, I. Manners and A. S. Weller, Chem. Commun., 2011, 47, 3763–3765.
8. J. R. Vance, A. P. M. Robertson, K. Lee and I. Manners, Chem.–Eur. J., 2011, 17, 4099–4103.
9. R. T. Baker, J. C. Gordon, C. W. Hamilton, N. J. Henson, P.-H. Lin, S. Maguire, M. Murugesu, B. L. Scott and N. C. Smythe, J. Am. Chem. Soc., 2012, 134, 5598–5609.
10. A. N. Marziale, A. Friedrich, I. Klopsch, M. Drees, V. R. Celinski, J. S. auf der Günne and S. Schneider, J. Am. Chem. Soc., 2013, 135, 13342–13355.
11. W. R. H. Wright, E. R. Berkeley, L. R. Alden, R. T. Baker and L. G. Sneddon, Chem. Commun., 2011, 47, 3177–3179.
12. A. P. M. Robertson, E. M. Leitao, T. Jurca, M. F. Haddow, H. Helten, G. C. Lloyd-Jones and I. Manners, J. Am. Chem. Soc., 2013, 135, 12670–12683.
13. T. Malakar, L. Roy and A. Paul, Chem.–Eur. J., 2013, 19, 5812–5817.
14. W. C. Ewing, A. Marchione, D. W. Himmelberger, P. J. Carroll and L. G. Sneddon, J. Am. Chem. Soc., 2011, 133, 17093–17099.
15. V. Pons, R. T. Baker, N. K. Szymczak, D. J. Heldebrant, J. C. Linehan, M. H. Matus, D. J. Grant and D. A. Dixon, Chem. Commun., 2008, 6597–6599.
16. M. Käβ, A. Friedrich, M. Drees and S. Schneider, Angew. Chem., Int. Ed., 2009, 48, 905–907.
17. H₂B=NMeH and H₂B=NH₂, or close derivatives thereof, have been trapped by coordination to a metal centre by dehydrogenation of the parent amine-borane. See, for example, G. Alcaraz, L. Vendier, E. Clot and S. Sabo-Etienne, Angew. Chem., Int. Ed., 2010, 49, 918–920; M. C. MacInnis, R. McDonald, M. J. Ferguson, S. Tobisch and L. Turculet, J. Am. Chem. Soc., 2011, 133, 13622–13633; M. A. Esteruelas, I. Fernández, A. M. López, M. Mora and E. Oñate, Organometallics, 2014, 33, 1104–1107.
18. H. C. Johnson and A. S. Weller, J. Organomet. Chem., 2012, 721–722, 17–22.
19. C. J. Stevens, R. Dallanegra, A. B. Chaplin, A. S. Weller, S. A. Macgregor, B. Ward, D. McKay, G. Alcaraz and S. Sabo-Etienne, Chem.–Eur. J., 2011, 17, 3011–3020.
20. C. A. Jaska, K. Temple, A. J. Lough and I. Manners, J. Am. Chem. Soc., 2003, 125, 9424–9434.
21. H. C. Johnson, A. P. M. Robertson, A. B. Chaplin, L. J. Sewell, A. L. Thompson, M. F. Haddow, I. Manners and A. S. Weller, J. Am. Chem. Soc., 2011, 133, 11076–11079.
22. A. T. Lubben, J. S. McIndoe and A. S. Weller, Organometallics, 2008, 27, 3303–3306.
23. L. P. E. Yunker, R. L. Stoddard and J. S. McIndoe, J. Mass Spectrom., 2014, 49, 1–8.
24. X. Yang and M. B. Hall, J. Organomet. Chem., 2009, 694, 2831–2838.
25. K. Ghatak and K. Vanka, Comput. Theor. Chem., 2012, 992, 18–29.
26. G. Bénac-Lestrille, U. Helmstedt, L. Vendier, G. Alcaraz, E. Clot and S. Sabo-Etienne, Inorg. Chem., 2011, 50, 11039–11045.
27. V. Butera, N. Russo and E. Sicilia, Chem.–Eur. J., 2011, 17, 14586–14592.
28. X. Chen, J.-C. Zhao and S. G. Shore, J. Am. Chem. Soc., 2010, 132, 10658–10659.
29. W. C. Ewing, P. J. Carroll and L. G. Sneddon, Inorg. Chem., 2013, 52, 10690–10697.
30. A. B. Chaplin and A. S. Weller, Eur. J. Inorg. Chem., 2010, 5124–5128.
31. I. Koehne, T. J. Schmeier, E. A. Bielinski, C. J. Pan, P. O. Lagaditis, W. H. Bernskoetter, M. K. Takase, C. Würtele, N. Hazari and S. Schneider, Inorg. Chem., 2014, 53, 2133–2143.
32. L. S. Santos and J. O. Metzger, Rapid Commun. Mass Spectrom., 2008, 22, 898–904.
33. D. Guironnet, L. Caporaso, B. Neuwald, I. Göttker-Schnetmann, L. Cavallo and S. Mecking, J. Am. Chem. Soc., 2010, 132, 4418–4426.
34. ESI-MS has been used to analyse the metal-free product of dehydropolymerisation. See, for example, mass spectra reported in ref. 4, 6 and 12.
35. Calculations were run with the Gaussian suite of programs and employed the BP86 functional. Rh and P centres described with the Stuttgart RECPs and associated basis set with added d-orbital polarisation on P (ζ = 0.387) and 6-31G** basis sets for all other atoms. Free energies are reported in the text, based the gas-phase values, incorporating corrections for dispersion effects using Grimme's D3 parameter set (i.e. BP86-D3) and solvent (C₆H₅F, PCM approach). See ESI† for references and full details.
36. R. Dallanegra, A. B. Chaplin and A. S. Weller, Angew. Chem., Int. Ed., 2009, 48, 6875–6878.
37. X. Chen, J.-C. Zhao and S. G. Shore, Acc. Chem. Res., 2013, 46, 2666–2675.
38. V. Butera, N. Russo and E. Sicilia, ACS Catal., 2014, 4, 1104–1113.
39. D. A. Addy, J. I. Bates, M. J. Kelly, I. M. Riddlestone and S. Aldridge, Organometallics, 2013, 32, 1583–1586.
40. Experimentally, addition of sequential equivalents of H₃B·NMeH₂ to 1 under a sparge of Ar to remove H₂ resulted in a reduced yield of 5b with significant amounts of unidentified decomposition products formed.
41. When H₃B·NMe₂H is added to the amino-borane complex 4a* significant (∼35%) quantities of the corresponding linear diborazane are observed, suggesting that under these conditions of a high local concentration of H₂B=NMe₂ the B–N bond forming reaction is kinetically competent. See ref. 19. This experimental observation is consistent with the essentially similar barriers to dehydrogenation and B–N coupling calculated here for the secondary amine-borane. At lower concentrations of amine-borane used in this study dimerisation to form [H₂B=NMe₂]₂ dominates and the diborazane is not observed.
42. P. M. Zimmerman, A. Paul, Z. Zhang and C. B. Musgrave, Inorg. Chem., 2009, 48, 1069–1081.
43. L. J. Sewell, G. C. Lloyd-Jones and A. S. Weller, J. Am. Chem. Soc., 2012, 134, 3598–3610.

---

Footnotes

† Electronic supplementary information (ESI) available: Full experimental details, ESI-MS, NMR spectra, details of X-ray crystallographic analysis and full computational details. CCDC 971346, 971347 and 988696. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4sc00735b

‡ These authors contributed equally.

---