Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evaluating metal–organic frameworks for natural gas storage†
Jarad A.
Mason
a,
Mike
Veenstra
b and
Jeffrey R.
Long
*a
aDepartment of Chemistry, University of California, Berkeley, CA 94720, USA. E-mail: jrlong@berkeley.edu
bFord Motor Company, Research and Advanced Engineering, Dearborn, MI 48121, USA
First published on 7th November 2013
Abstract
Metal–organic frameworks have received significant attention as a new class of adsorbents for natural gas storage; however, inconsistencies in reporting high-pressure adsorption data and a lack of comparative studies have made it challenging to evaluate both new and existing materials. Here, we briefly discuss high-pressure adsorption measurements and review efforts to develop metal–organic frameworks with high methane storage capacities. To illustrate the most important properties for evaluating adsorbents for natural gas storage and for designing a next generation of improved materials, six metal–organic frameworks and an activated carbon, with a range of surface areas, pore structures, and surface chemistries representative of the most promising adsorbents for methane storage, are evaluated in detail. High-pressure methane adsorption isotherms are used to compare gravimetric and volumetric capacities, isosteric heats of adsorption, and usable storage capacities. Additionally, the relative importance of increasing volumetric capacity, rather than gravimetric capacity, for extending the driving range of natural gas vehicles is highlighted. Other important systems-level factors, such as thermal management, mechanical properties, and the effects of impurities, are also considered, and potential materials synthesis contributions to improving performance in a complete adsorbed natural gas system are discussed.
Natural gas storage
Natural gas has the potential to replace petroleum as the world's primary fuel for transportation. Consisting mainly of methane (CH4), natural gas has the highest H to C ratio of any fossil fuel, resulting in less CO and CO2 released per unit of energy generated.1 Lower sulfur and nitrogen contents also lead to lower SOx and NOx emissions, making natural gas a significantly cleaner burning fuel than gasoline.2 Indeed, initial field tests found up to 86% less CO, 26% less CO2, and 77% less NOx emissions after converting gasoline cars to run on natural gas.3 In addition, recent engineering advances in horizontal drilling and hydraulic fracturing have led to a rapid increase in global natural gas reserves, driving the price of natural gas below that of gasoline in many countries.4In spite of this, several challenges have prevented the widespread use of natural gas in vehicles. Most importantly, the volumetric energy density of natural gas at ambient temperature and pressure is only 0.04 MJ L−1, compared to 32.4 MJ L−1 for gasoline.5 The volumetric energy density can be increased by compression or liquefaction, but both of these solutions are costly and poorly suited for light-duty passenger vehicles. For instance, compressed natural gas (CNG) requires expensive multi-stage compressors that consume energy, as well as heavy, bulky fuel tanks that reduce passenger and cargo space. Even with compression to 250 bar, the energy density of CNG (near 9 MJ L−1) is only 26% that of gasoline,2a leading to a significant reduction in the driving range of a vehicle. Moreover, CNG refueling stations are not yet common enough for convenient refueling and are costly to build.6
As a result of the low critical temperature of CH4 (190.6 K, Table 1), natural gas cannot be liquefied by compression alone, and cryogenic cooling is necessary to store liquefied natural gas (LNG). While the volumetric energy density of LNG can reach 20.8 MJ L−1 (64% of gasoline),5 the overall system energy density is reduced due to the insulation required to maintain a low temperature and prevent boil-off. Additionally, the high cost of cooling systems and complications of handling a cryogenic fuel make LNG unlikely to find much application in the transportation sector beyond commercial trucking and public transportation.7
As an alternative to CNG and LNG, using adsorbents to store natural gas at higher densities at ambient temperature and moderate pressures has been an active area of research since the early 1970s.10a Significantly, adsorbents that operate at relatively low pressures should allow the use of inexpensive on-board fuel tanks and single-stage compressors. Lower storage pressures also facilitate at-home refueling,7 which would reduce the large investment needed to build a new refueling infrastructure since natural gas distribution networks are already connected to many homes throughout the world.6 Additionally, adsorbed natural gas (ANG) systems would permit the use of lightweight, conformable fuel tanks that can be more optimally integrated into the limited space available within a small car.11 Note that in addition to natural gas powered cars, which are the focus of this work, ANG systems have also been evaluated for use in mobile natural gas tankers and for large-scale, stationary storage on natural gas distribution pipelines.12 Although it is important to evaluate and optimize a similar set of adsorbent properties for each of these applications, the relevant storage conditions can differ significantly.
While early efforts in ANG storage focused primarily on zeolites, their relatively low surfaces areas of less than 1000 m2 g−1 resulted in insufficient CH4 capacities.7,10 With considerably higher surface areas, activated carbons have been the most studied class of materials for ANG over the last several decades.13 A large portion of research has involved investigating the effects of surface area, pore size, and pore shape on the CH4 adsorption properties of different carbons. Indeed, it was demonstrated that slit-shaped pores with a diameter of 7.6 Å, which can accommodate two layers of CH4, are ideal for maximizing the volumetric density of CH4 stored at 35 bar and 25 °C.14,15 Note that 35 bar has been widely used as a standard pressure for evaluating adsorbents for ANG storage, as this has represented the maximum pressure achievable by most inexpensive single-stage compressors.16 Additionally, strategies for compacting and shaping activated carbons to optimize packing inside a storage tank have been explored in depth,1 and prototype activated carbon ANG systems have been demonstrated and tested.17
In 2012, the US Department of Energy set new CH4 storage targets for absorbents at 350 cmSTP3 cmadsorbent−3 (v/v)18 and 0.5 gCH4 gadsorbent−1 (699 cm3STP g−1).19 Assuming a 25% loss in volumetric capacity due to packing an adsorbent inside a fuel tank, the target of 350 v/v is required for an ANG system to have a volumetric energy density of 263 v/v, equivalent to that of CNG at 250 bar and 25 °C. The highest reported volumetric CH4 capacities for activated carbons are in the range of 100–170 v/v,20 well below the energy density of CNG, and computational studies have predicted a theoretical maximum volumetric capacity for carbons of 198 v/v at 34 bar and 25 °C.14 Accordingly, a next generation of adsorbents is required to meet these storage targets without moving to higher adsorption pressures or lower temperatures, both of which would add significant complexity and cost to an ANG vehicle.
Owing to their high porosity and tunable pore surfaces, metal–organic frameworks have received significant attention as a new class of adsorbents.21 While early research on these materials for gas storage applications was mostly related to H2,22 a growing number of frameworks have been evaluated for CH4 storage.23,24 Significantly, several metal–organic frameworks have reported CH4 capacities comparable to or exceeding those of the best activated carbons; however, inconsistencies in reporting adsorption results and a lack of comparative studies have made it challenging to compare the performance of different materials. Here, we discuss the most important material properties for evaluating both new and existing metal–organic frameworks for natural gas storage and briefly review recent work. In this context, six metal–organic frameworks and an activated carbon, with a range of surface chemistries, pore structures, and surface areas representative of the most promising adsorbents for CH4 storage, are evaluated in detail.
High-pressure adsorption
All evaluations of adsorbents for natural gas storage rely on the measurement of accurate high-pressure adsorption isotherms. However, high-pressure experiments introduce several complexities, both in terms of collecting isotherm data and interpreting the results, that are not as significant at lower pressures. For instance, there is often inconsistent usage of the terms excess, total, and absolute when describing high-pressure adsorption capacities, which can lead to needless uncertainty when comparing the uptakes of different materials.Excess, total, and absolute adsorption
At a fundamental level, a gas is considered to be adsorbed when attractive forces from a surface result in a greater density of gas molecules than would normally be present at the same temperature, T, and pressure, P. For adsorption on a two-dimensional surface, the strength of the interaction between the gas and surface will decrease with increasing distance until the attractive forces of the surface become negligible and only bulk or free gas molecules are present. At this distance, an imaginary line, known as the Gibbs dividing surface, can be drawn to divide the total free volume into adsorbed and bulk regions (Fig. 1a).25 The absolute amount adsorbed, nabs, is defined simply as the total number of molecules that are in the adsorbed region. Unfortunately, absolute adsorption cannot be directly measured since it is not possible to determine the location of the Gibbs dividing surface or the size of the adsorbed region experimentally.26 As a result, all adsorption measurements give excess adsorption, nex, which is the difference between the absolute adsorption amount and the amount of bulk gas that would have been present in the adsorbed region, Va, in the absence of a surface (eqn (1)).26| nex = nabs − Vaρbulk(P,T) | (1) |
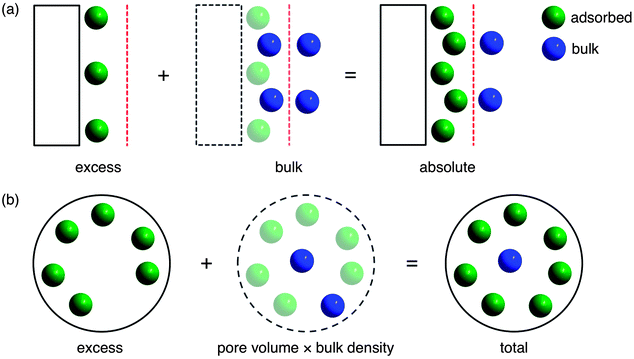 | ||
| Fig. 1 (a) For adsorption on a two-dimensional surface (rectangle), the Gibbs dividing surface (red) divides the free volume into two regions where gas molecules are either in an adsorbed (green) or bulk (blue) state.25Absolute adsorption, which includes all gas molecules in the adsorbed state, is the sum of the experimentally measured excess adsorption and the bulk gas molecules that would have been present in the adsorbed region in the absence of a surface. (b) For porous materials, the total adsorption includes all gas molecules inside the total pore volume, which corresponds to the sum of the excess adsorption and the bulk gas that would have been present in the pore volume in the absence of adsorption.28 Note that for microporous materials, the total adsorption is often used as an approximation for absolute adsorption,29 since it is not possible to determine the location of the Gibbs dividing surface experimentally.26 | ||
Since it is not possible to determine Va experimentally, there is no straightforward method for calculating absolute adsorption from the measured excess adsorption. Instead, the total adsorption,27,28ntot, which includes all gas molecules within the pores of an adsorbent, is often used as an approximation for absolute adsorption (Fig. 1b).29,30 Total adsorption can be calculated from the excess adsorption using eqn (2) and the experimentally measured total pore volume, Vp. Note that the total pore volume is typically determined from an N2 adsorption isotherm at 77 K by assuming all pores have been completely filled with condensed N2 at a sufficiently high P/P0, where P0 is the N2 saturation pressure.31 Based on the Gurvich rule,32,33 the total pore volume can be calculated by assuming that the molar volume of liquid N2 is the same regardless of the size or surface chemistry of the pore it is condensed within. For microporous materials with negligible external surface areas, which have a well-defined plateau in the N2 adsorption isotherm at 77 K, the exact P/P0 used is not particularly important. However, a P/P0 of 0.9–0.95 is typical and will include any pores less than 200–400 Å in the total volume calculation.34 Other adsorbates, such as CH4, can be used similarly to determine the total pore volume, but results generally do not vary significantly as long as all pores are equally accessible to the different probe molecules.35 In most cases, small errors in the total pore volume do not have a significant impact on the calculated total adsorption.36
| ntot = nex + Vpρbulk(P,T) | (2) |
For gas storage applications, the total adsorption is most relevant for comparing the capacities of different adsorbents, as it is an intrinsic property of a material that represents the total amount of gas that can be stored inside a material’s pores.28 Since the density of gas in the bulk phase, ρbulk, is significant at high pressures, there is usually a large difference between the excess and total amount adsorbed at conditions relevant to natural gas storage. As a result, inconsistent usage of the terms excess, absolute, and total makes comparing CH4 capacities of different materials challenging, and it is always important to specify clearly the type of adsorption capacity that is being reported.
High-pressure adsorption measurements
Due primarily to the large pressure range that is covered and the increasing nonideal behavior of gases above ambient pressure, adsorption experiments are inherently more difficult to perform accurately at high pressures than at low pressures. This can lead to large errors that make it challenging to compare the properties of different materials. Most commercial high-pressure adsorption instruments operate using either a gravimetric or volumetric measurement technique. At a basic level, gravimetric instruments measure the amount of CH4 adsorbed by using a balance to record the change in weight of a sample at different equilibrium pressures of CH4, while volumetric instruments record the change in pressure when dosing CH4 from a calibrated volume to a volume containing the sample. In both cases, it is important to be aware of the most common issues that can affect the quality of the experimental data.For both gravimetric and volumetric adsorption measurements, He is used to determine the precise volume occupied by the adsorbent inside the sample holder, which is needed for buoyancy corrections and free space calculations in gravimetric and volumetric experiments, respectively. Techniques for performing these corrections have been discussed in detail elsewhere,28,37 but it is worth emphasizing that errors in buoyancy and free space calculations can significantly affect the accuracy of adsorption data (Fig. S17†). Note that for both corrections, He adsorption by the sample is assumed to be negligible, and as such, it is best to perform He measurements at the low pressures and high temperatures where this is most likely to be true.26,38
Regardless of the exact method used to perform buoyancy or freespace corrections, there will always be many other potential sources of error in high-pressure experiments, such as volume calibrations, thermocouple readings, pressure transducer readings, sample mass measurements, nonideality corrections and temperature gradients.37c Therefore, it is essential to measure background CH4 adsorption isotherms with empty sample holders, or with a nonadsorbing material similar in volume to a typical sample, at all potential analysis temperatures and pressures.28 Ensuring that background adsorption is negligible under the exact same conditions as in an actual experiment confirms that all calibrations, corrections, measurements, and calculations are valid, which is critical for verifying the accuracy of the resulting adsorption data. Note that this is equally important for volumetric, gravimetric, commercial, and custom-built high-pressure instruments.
Additionally, for gravimetric adsorption measurements, it is particularly important to ensure that no impurities are present in the CH4 used, as even small quantities of more strongly adsorbing impurities, such as heavier hydrocarbons or water, can lead to large errors in the measured uptake. Similarly, large errors in volumetric measurements can often result from the fact that high-pressure sample holders, which are typically constructed from stainless steel, are very heavy compared to a typical sample. As a result, it is usually not practical to weigh an activated adsorbent in a fully assembled sample holder, as is common for low-pressure experiments. Thus, it can be difficult to obtain an accurate sample mass, which can lead to significant errors in measured capacities that have a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dependence on the amount of sample present. One potential solution is to measure the surface area of a sample directly prior to a high-pressure measurement in a fully assembled high-pressure sample holder. By confirming that the surface area is as expected, uncertainties associated with sample mass can be mostly eliminated.
1 dependence on the amount of sample present. One potential solution is to measure the surface area of a sample directly prior to a high-pressure measurement in a fully assembled high-pressure sample holder. By confirming that the surface area is as expected, uncertainties associated with sample mass can be mostly eliminated.
Evaluating metal–organic frameworks
Although high-pressure CH4 adsorption isotherms have been measured for almost one hundred metal–organic frameworks, their CH4 uptakes have been reported in a variety of different units and at a range of pressures and temperatures, which makes evaluating the relative performance of a particular compound difficult. To facilitate comparisons between existing materials for which ambient temperature, high-pressure CH4 adsorption isotherms have been published, Table 2 lists the total CH4 uptake of all metal–organic frameworks at conditions as close to 35 bar and 25 °C as possible. To make comparisons between materials more meaningful, all isotherm data that was originally reported in terms of excess adsorption has been converted to total adsorption using each framework's measured pore volume and the bulk gas density from the NIST Refprop database at the appropriate temperature and pressure (eqn (2)).8 Note, however, that in a number of instances there was no indication of whether reported data were given in terms of excess, total, or absolute adsorption, adding significant uncertainty to comparisons of these uptakes to those of other materials.In almost all standard adsorption measurements, the amount adsorbed is determined per unit mass, not volume, of adsorbent. However, the amount of CH4 adsorbed per volume, which ultimately determines the amount of natural gas that can be stored in a given fuel tank, has to be calculated using the density of a material. For metal–organic frameworks, the ideal crystallographic density has commonly been used to convert gravimetric adsorption capacities to a volumetric capacity that represents the maximum possible volumetric uptake in the absence of any loss in density from packing actual particles together inside a fuel tank. This method of calculating volumetric capacities certainly over-estimates what is realistically achievable, but it is still useful for initial comparisons between adsorbents, provided the crystallographic densities used are appropriate. Here, a substantial effort was made to ensure that all crystallographic densities were as representative as possible of the framework during CH4 adsorption, which mainly involved confirming that both metal-bound and free solvent molecules from solvated crystal structures were not included in density calculations. Based upon these and other observations made while surveying published CH4 adsorption data for metal–organic frameworks, we make the following recommendations for future evaluations of new frameworks for ANG storage:
(1) Report background high-pressure CH4 adsorption isotherms for an empty sample holder (or sample holder with a nonadsorbing solid) at all measured temperatures and pressures as supplementary information.28,39
(2) Specify whether all isotherms are reported in terms of excess, total, or absolute adsorption. Methods used to convert experimental excess adsorption data to total or absolute adsorption should be detailed, including any assumptions made about the size of the adsorbed volume.28 If a pore volume was used to calculate total adsorption, it should be reported along with the isotherm used to calculate it.
(3) When volumetric uptakes are reported, the density used should be given and the type of density (e.g. crystallographic, bulk, tap, pellet) specified.40 When crystallographic densities are used, details of their calculation should be provided, including at a minimum: unit cell volume, unit cell content, and any potential differences between the state of the framework when the unit cell was determined and when adsorption isotherms were measured, which may involve desolvation, removal of excess ligand, framework flexibility, and/or different measurement temperatures.
(4) If the unit cm3STP is used to report adsorption data, the standard temperature and pressure should be defined.
(5) When isosteric heats of adsorption are reported, the method used to calculate them should be specified. Note that stating that the Clausius–Clapeyron relation was used is not sufficient, as this does not give any indication about how interpolations between measured data points were made.
(6) When mathematical models are used to fit experimental adsorption isotherms, all fitted parameters should be given, and the quality of the isotherm fits should be illustrated.
CH4 adsorption isotherms
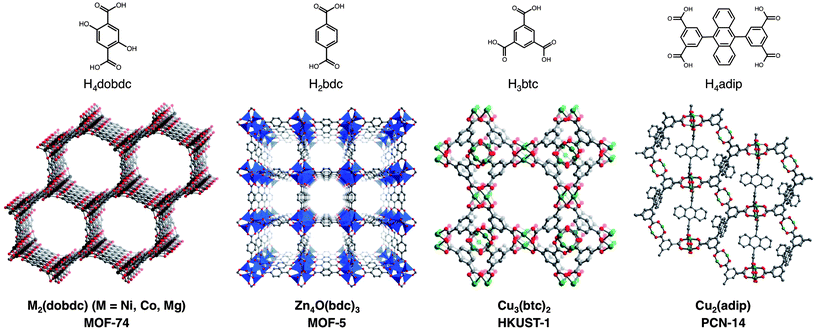
In examining Table 2, there are many cases, particularly for the highest capacity frameworks, where CH4 adsorption isotherms have been reported for the same material in multiple publications with inconsistent results. This makes it challenging to compare different frameworks and to understand the effects of different characteristics of the materials on CH4 uptake. For example, HKUST-1 has been reported to have total CH4 uptakes at 35 bar ranging between 184 and 220 v/v. By synthesizing and activating a selection of the most promising compounds in the same laboratory and measuring high-pressure isotherms on the same instrument, evaluating and comparing their CH4 adsorption properties becomes more straightforward. To this end, the six metal–organic frameworks depicted in Fig. 2, along with an activated carbon for comparison, were chosen for a detailed evaluation. The seven materials have features that are common to many of the adsorbents that have shown the highest gravimetric and volumetric CH4 uptakes at 35 bar, including strong adsorption sites, pores shaped by Cu2-paddlewheel units, and high surface areas.With modest gravimetric surface areas of 1500–2000 m2 g−1, the M2(dobdc) (M = Ni, Co, Mg; dobdc4− = 2,5-dioxido-1,4-benzenedicarboxylate; M-MOF-74, CPO-27-M) compounds have one-dimensional hexagonal channels featuring square pyramidal metal cations that have been shown to act as strong adsorption sites for many small gas molecules.41,42 The compounds Cu3(btc)2 (btc3− = 1,3,5-benzenetricarboxylate; HKUST-1)43,44 and Cu2(adip) (adip4− = 5,5′-(9,10-anthracenediyl)di-isophthalate; PCN-14)44c,45 are built from Cu2-paddlewheels that also contain exposed metal cations upon desolvation; however, their pore structures are significantly more complicated than M2(dobdc), with several differently sized pores and pore windows. Significantly, PCN-14 has been widely cited as one of the best existing metal–organic frameworks for CH4 storage, based upon its reported total volumetric uptake of 230 v/v at 17 °C and 35 bar.45a The compound Zn4O(bdc)3 (bdc2− = 1,4-benzene-dicarboxylate; MOF-5, IRMOF-1) has a high Langmuir surface area of 3995 m2 g−1, but does not contain any inherently strong adsorption sites for CH4.21a,24a,46 Indeed, its pore surface is more similar to that of an activated carbon. For comparison, the activated carbon AX-21, which has an exceptionally high Langmuir surface area of 4880 m2 g−1 and is one of many activated carbons that have been studied in detail for ANG storage, was also evaluated.47
After synthesis, surface areas and pore volumes were measured for all seven materials to ensure samples were fully activated and of high quality (Fig. S7–S15†). High-pressure CH4 adsorption isotherms from 0 to 100 bar were then measured for each material at −25, 25, 38, and 50 °C. Experimentally measured excess adsorption isotherms were converted to total adsorption using total pore volumes, as determined from N2 isotherms at 77 K (P/P0 = 0.9), and the bulk gas density at each temperature and pressure from the NIST Refprop database (eqn (2)).8 Volumetric adsorption was calculated using the crystallographic densities of desolvated structures at as near ambient temperature as possible (Table S2†).
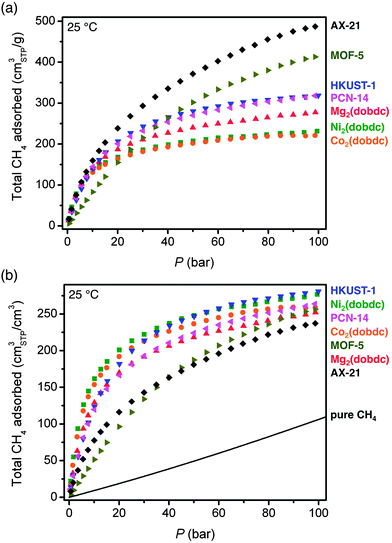
In Fig. 3, the 25 °C high-pressure CH4 isotherms of all materials measured in this work are compared in terms of total gravimetric and volumetric adsorption. Of the materials measured, AX-21 has the highest gravimetric uptake at all pressures. For the metal–organic frameworks, HKUST-1 has the highest gravimetric uptake (255 cm3STP g−1 = 0.183 gCH4 g−1) at 35 bar, but the capacity of MOF-5 is highest at pressures greater than 40 bar. At high pressures, the gravimetric capacity is reasonably well correlated with the gravimetric surface area (Fig. S38†), which is consistent with previous observations for both metal–organic frameworks and activated carbons.7,13,24f,h,61 Indeed, the metal–organic frameworks in Table 2 with the three highest reported gravimetric uptakes at 25 °C and 35 bar all have exceptionally high specific surfaces areas: DUT-49 with an uptake of 0.26 gCH4 g−1 and a surface area of 5476 m2 g−1, NU-111 with an uptake of 0.24 gCH4 g−1 and a surface area of 4930 m2 g−1, and PCN-68 with an uptake of 0.24 gCH4 g−1 and a surface area of 5109 m2 g−1.48,50
In addition to the different CH4 capacities of the frameworks studied here, there are important differences in the shapes of their adsorption isotherms. Specifically, AX-21 and MOF-5 have shallower isotherms at low pressures and do not begin to approach saturation until much higher pressures than M2(dobdc), HKUST-1, and PCN-14. This is expected based on the lack of strong adsorption sites in AX-21 and MOF-5, and has important consequences for the amount of CH4 that can actually be delivered by each material.
Importantly, as will be discussed in detail below, achieving a high volumetric adsorption capacity is much more critical than a high gravimetric capacity for extending the driving range of a vehicle. While the overall shapes of the volumetric isotherms are similar to the gravimetric ones, the trends in capacity differ significantly. For instance, Ni2(dobdc) and Co2(dobdc) have the highest uptakes at lower pressures, and Ni2(dobdc) and HKUST-1 have the highest total volumetric uptakes at 35 bar: 230 and 225 v/v, respectively. Note that the total volumetric uptake of Ni2(dobdc) is the highest value yet reported for any metal–organic framework at 25 °C and 35 bar. Although PCN-14 has been widely cited as the best existing metal–organic framework for volumetric CH4 storage, Ni2(dobdc) and HKUST-1 have significantly higher volumetric capacities at 35 bar and 25 °C.
It is worth noting that in contrast to gravimetric adsorption, the volumetric uptake at 35, 65, or 100 bar, does not correlate with volumetric surface area (Fig. S39†). Indeed, MOF-5 has a volumetric surface area 30% greater than Ni2(dobdc), but a volumetric uptake that is lower at all pressures measured here of less than 100 bar. This highlights the importance of the density and strength of specific CH4 adsorption sites, rather than just surface area and pore volume, for achieving high volumetric capacities.
Methane adsorption sites in Ni2(dobdc) and HKUST-1
While Ni2(dobdc) and HKUST-1 have the highest volumetric uptakes of all metal–organic frameworks reported to date (Table 2), they are still well short of the 350 v/v target that is expected to achieve a volumetric energy density similar to that of CNG. In designing a next generation of improved framework materials to meet this target, it is useful to consider the fundamental mechanisms responsible for the high volumetric uptakes of Ni2(dobdc) and HKUST-1. Detailed powder X-ray and neutron diffraction experiments have previously been used in several studies to identify the strongest CH4 adsorption sites in both structures.42,44 Note that the only structural study of CH4 in M2(dobdc) was for the Mg analogue,42 but based on the similar adsorption isotherms and previous structural studies with H2 and CO2,41d–f,i,j,l,m it is reasonable to expect similar CH4 binding sites within Ni2(dobdc).In both HKUST-1 and Ni2(dobdc), the exposed Cu2+ and Ni2+ cations act as strong binding sites that can contribute a maximum of 98 v/v and 172 v/v, respectively, to the total volumetric capacity when one CH4 is bound to each metal. These are the only strong binding sites expected in Ni2(dobdc), and just weaker secondary adsorption sites should be available for CH4 after the Ni2+ sites are fully occupied.42 In contrast, HKUST-1 has additional strong adsorption sites, located in the four windows of each octahedral cage, which are populated at the same time as the Cu2+ sites,44 suggesting both adsorption sites have similar CH4 binding energies (Fig. 4). These window sites bind CH4 strongly due to several close interactions, in the range 2.7–3.2 Å, between framework O atoms and an adsorbed CH4 molecule (Fig. S47†).
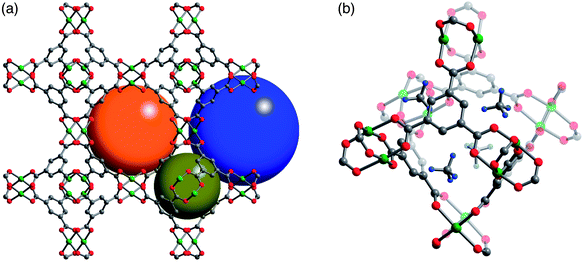 | ||
| Fig. 4 (a) Crystal structure of HKUST-1 highlighting the three different types of pores in the structure that have diameters of roughly 5 Å (dark yellow), 11 Å (orange), and 13.5 Å (blue). Note that the open coordination site of the exposed Cu2+ cations is only directed into the 13.5 Å (blue) pores. Atomic coordinates are taken from a desolvated crystal structure at 100 K.51 (b) Location of adsorbed CD4 molecules at the four windows sites of an octahedral cage. The atomic coordinates are taken from a powder neutron diffraction structure with a loading of 1.1 CD4 per Cu2+ at 4 K.44c Green, gray, red, and light blue spheres represent Cu, C, O, and D atoms, respectively; H atoms have been omitted for clarity. | ||
Significantly, the window sites can contribute an additional 65 v/v to the volumetric capacity of HKUST-1, bringing the total contribution of strong adsorption sites to 163 v/v, just below that of Ni2(dobdc) (172 v/v). On the other hand, there is a more pronounced difference in the contribution of strong adsorption sites to the total gravimetric capacity of each material at 144 cm3STP g−1 and 185 cm3STP g−1 for Ni2(dobdc) and HKUST-1, respectively. Further, while both materials have similar volumetric surface areas (Table S1†), HKUST-1 has a significantly greater gravimetric surface area that can be expected to lead to a higher gravimetric density of weak CH4 adsorption sites. Taken together, the similar volumetric and different gravimetric capacities of strong and weak adsorption sites can help explain the experimental CH4 isotherms, wherein both materials have similar volumetric uptakes at 35 bar, but HKUST-1 has a much higher gravimetric uptake. In order to explain why Ni2(dobdc) has a steeper isotherm at lower pressures, it is necessary to also consider differences in the binding energies of the strong adsorption sites of each material.
Isosteric heats of adsorption
To gain further insight into differences between the seven materials, isosteric heats of adsorption (Qst), which represent the average binding energy of an adsorbing molecule at a specific surface coverage, were determined as a function of the amount of CH4 adsorbed, n, by using the Clausius–Clapeyron relation (eqn (3)).52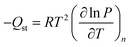 | (3) |
In order to employ this relation, it is first necessary to fit the high-pressure isotherm data with a mathematical model, such that it is possible to interpolate between measured data points to determine the exact pressures that correspond to the same amount adsorbed at different temperatures. Regardless of the mathematical model used, it is important to remember that the Clausius–Clapeyron equation is fundamentally a thermodynamic relation that describes a phase transition of a gas from a bulk to adsorbed state, and as such, it is based on the absolute amount adsorbed, which includes all gas molecules that experience an attractive potential from the adsorbent surface.26d For microporous materials, the total adsorption is often used as an approximation for absolute in heat of adsorption calculations, as most gas molecules inside micropores will have some degree of interaction with the pore surface.22a,29 In contrast to low-pressure experiments, there is a significant difference between excess and total adsorption at high pressures, and it is critical that the total adsorption is used for all thermodynamic calculations,36 unless the relevant thermodynamic relations have been specifically altered for excess quantities.26d
Virial-type equations have been routinely used to fit high-pressure adsorption data for metal–organic frameworks,53 despite the fact that most virial parameters lack any physical meaning.54 In contrast, equations that are based on physical models of adsorption, such as the Dubinin–Astakhov (DA)55 and multi-site Langmuir equations,56 have been more widely used in analyzing CH4 isotherms of activated carbons.57 One major advantage of fitting isotherm data with physically relevant parameters is that it makes extrapolation to temperatures and pressures that were not experimentally measured more meaningful, which is important not only for calculating heats of adsorption but also for process modeling and systems design. Additionally, errors in high-pressure isotherm data can be significant, especially when compared to low-pressure experiments, and leveraging at least some physical constraints on the fitting parameters can help ensure that the resulting isosteric heats are reasonable. Here, single- and dual-site Langmuir models were used to fit the adsorption data of each material at all measured temperatures with one set of parameters (see ESI† for details). Several recent studies have demonstrated the ability of Langmuir-type equations to successfully model adsorption in metal–organic frameworks, especially those that have well-defined adsorption sites on the pore surface.36,41n–r,58
The importance of the method used for calculating Qst can be illustrated by examining the heats of adsorption originally reported for PCN-14, wherein the low-coverage binding enthalpy of −30 kJ mol−1 is nearly double the value of −18 kJ mol−1 determined in this work (Fig. S37†).45a It was suggested that this record high heat of adsorption was largely responsible for the high volumetric uptake of PCN-14, but no details of the Qst calculations were reported. While PCN-14 certainly does exhibit high volumetric uptake, the reported values of Qst, which influenced several follow-up computational studies,24h,44c,45b can hinder efforts to understand the underlying adsorption mechanisms that are responsible and to design improved materials.
For all seven materials evaluated in this work, the isosteric heats of adsorption as a function of the total CH4 loading are plotted in Fig. 5. As expected based upon its steep isotherm and high volumetric uptake, Ni2(dobdc) has the highest Qst at low coverage, followed by Co2(dobdc) > Mg2(dobdc) > PCN-14 ∼ HKUST-1 > AX-21 > MOF-5. It is interesting to note differences in the shape of Qst curves as the CH4 loading is increased. For example, the M2(dobdc) compounds have relatively constant binding energies at low loadings that begin to decrease as the exposed metal cation sites become populated. On the other hand, PCN-14 and HKUST-1 have heats of adsorption near −17 kJ mol−1 regardless of the amount of CH4 adsorbed, confirming that the exposed Cu2+ cations and window adsorption sites in both materials have similar CH4 binding strengths. Likewise, MOF-5 exhibits a constant, but much weaker, binding energy of −12.3 kJ mol−1. These differences are consistent with the shapes of the adsorption isotherms, for which the M2(dobdc) compounds have the steepest rises at low pressures, while MOF-5 is the most shallow. Note that the gradual decline in the isosteric heat of adsorption of AX-21 from 15.5 to 12.4 kJ mol−1 is likely due to the wide distribution of pore sizes present in the activated carbon, whereby smaller pores will tend to have stronger interactions with CH4 than larger pores.
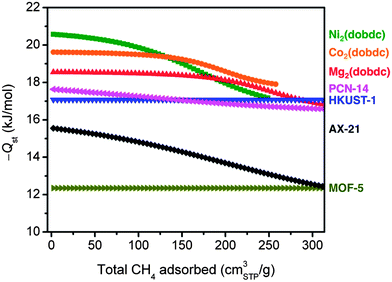 | ||
| Fig. 5 Isosteric heats of adsorption, −Qst, at 25 °C as a function of the total amount of CH4 adsorbed. | ||
It is important to emphasize that while the single- and dual-site Langmuir models used here describe the experimental adsorption data very well over a wide temperature and pressure range, there may be other models that result in equally good, or in some cases perhaps even better, fits to the data. Some of these models may involve an increase in the isosteric heat of adsorption at high CH4 loadings due to the contribution of CH4⋯CH4 interactions at high pressures, as has been reported for several frameworks.59 Unfortunately, the experimental high-pressure adsorption data is typically not accurate enough to determine reliably whether such an increase actually exists in any of the materials studied here. However, it is worth noting that several studies have clearly shown that using excess adsorption isotherms to calculate Qst can lead to large increases in Qst at higher loadings that do not occur when using absolute or total adsorption.28,36 Moreover, the contribution of CH4⋯CH4 interactions to the overall heat of adsorption has been estimated to be less than 2 kJ mol−1, which would be difficult to detect accurately at the high pressures where it would be most influential and the adsorption data is least accurate.60 Regardless, the differences in isosteric heats of adsorption at pressures most relevant to ANG storage are clear, and these have important consequences for the amount of CH4 that can actually be delivered by each material inside a vehicle.
Usable CH4 capacity
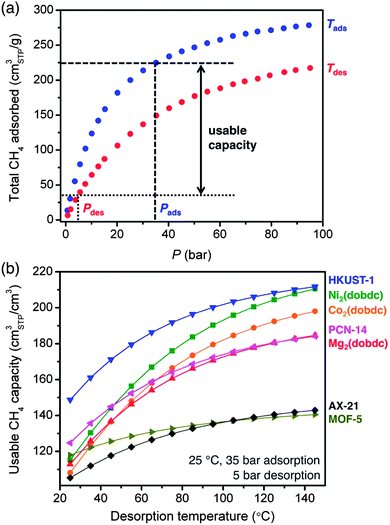
Comparing the 35 bar CH4 capacities of different adsorbents is useful for initial evaluations, but not all of this capacity will be accessible when delivering natural gas to an engine that requires a minimum inlet pressure to operate. As such, the usable CH4 capacity is defined as the amount of CH4 that can be delivered when decreasing from the filling or adsorption pressure to a specific desorption pressure (Fig. 6a).28 For ANG storage, the adsorption pressure is usually assumed to be 35 bar, since this is a typical benchmark for the maximum achievable pressure of inexpensive single-stage compressors.16 While 5 bar is commonly cited as a minimum desorption pressure,49,61 engines that can operate at inlet pressures as low as 3 bar are available and would allow for a greater usable CH4 capacity and increased vehicle driving range. Currently, most natural gas vehicles contain gasoline engines that have been retrofitted to run on natural gas and require inlet pressures of 5 to 10 bar. If the demand for natural gas vehicles increases dramatically, the minimum operating pressure may decrease as engines are built and optimized specifically to burn natural gas. It is important to note that the amount of CH4 retained by the adsorbent during desorption can also be reduced by heating, ideally taking advantage of waste heat from the engine.62The volumetric usable CH4 capacities of all materials evaluated here are plotted in Fig. 6b for adsorption at 35 bar and 25 °C and desorption at 5 bar and temperatures from 25 to 145 °C. Despite the fact that Ni2(dobdc) has a higher total volumetric uptake at 35 bar, HKUST-1 has the highest usable CH4 capacity for all calculated desorption temperatures. This is a direct result of the weaker interaction of CH4 with HKUST-1 than with Ni2(dobdc), which results in significantly less CH4 retained by HKUST-1 at 5 bar. Indeed, the usable CH4 capacity of Ni2(dobdc) is only 115 v/v for desorption at 25 °C, which is just 50% of its 35 bar capacity. In contrast, the usable capacity of HKUST-1 under the same conditions is 149 v/v, which is 66% of its 35 bar capacity.
The gravimetric usable CH4 capacity is plotted in Fig. S40† for the same adsorption–desorption conditions. In this case, AX-21 has the highest usable capacity at all desorption temperatures, while MOF-5 is the best metal–organic framework for desorption temperatures below 60 °C. Although HKUST-1 exhibits a higher total gravimetric uptake at 35 bar, its usable capacity is below that of MOF-5 unless the desorption temperature is increased. This is due to the weak interaction of MOF-5 with CH4 (−12 kJ mol−1), which results in only a small amount of CH4 adsorbed at 5 bar. Usable capacity plots as a function of desorption pressure are also given in the ESI† and show similar trends between materials, as is expected since decreasing the desorption pressure has a similar effect to increasing the desorption temperature (Fig. S41–S42†).
Adsorption at lower temperatures or higher pressures can also be considered as a strategy for increasing the usable capacity (Fig. S43–S46†). Indeed, by decreasing the adsorption temperature to −25 °C, the usable capacity of HKUST-1 reaches 222 v/v for desorption at 5 bar and 25 °C, which is 67% greater than for adsorption at 25 °C. However, a full systems-level analysis is necessary to determine whether the higher costs associated with cooling the fuel and the thermal management of the tank, or with compressing natural gas to higher pressures, would be worth the increase in usable capacity and driving range.
Of all the metal–organic frameworks previously evaluated by others and those studied here, HKUST-1 appears to be the most promising current framework for natural gas storage, as it features one of the highest usable volumetric capacities for CH4. A similar conclusion was also reached by others while this manuscript was in preparation,63 and it is perhaps not surprising that HKUST-1 was chosen by BASF for use in a prototype ANG van in 2007.64
Optimal binding enthalpy
The differences in the usable CH4 capacities between the materials studied illustrate the importance of both increasing capacity and optimizing binding enthalpy when designing improved adsorbents. If the binding enthalpy is too high, then too much CH4 will be retained at low pressures, decreasing the usable capacity. On the other hand, if the binding enthalpy is too low, then too little CH4 will be adsorbed at higher pressures. Using a single-site Langmuir model, it can be shown that the optimal binding enthalpy for CH4 adsorption at 35 bar and 25 °C and desorption at 5 bar is −17 kJ mol−1,65 exactly equal to that determined for HKUST-1 over the entire pressure range of 5 to 35 bar.Note that the optimal binding enthalpy is dependant on the exact desorption conditions used. Indeed, Fig. 7 shows the percentage of the saturation capacity that is usable at different binding energies and desorption temperatures. As the desorption temperature is increased, or desorption pressure decreased, the optimal binding enthalpy increases (see ESI† for details). Note that the simple analysis presented here ignores correlations between the adsorption enthalpy and entropy, but these correlations would be expected to lead to even larger increases in the optimal Qst as the desorption temperature is increased.66 Regardless, Fig. 7 illustrates the importance of optimizing binding enthalpy and the benefits of using higher desorption temperatures to maximize usable capacity. Nevertheless, employing a material with optimal binding enthalpy is useless if the density of adsorption sites having that enthalpy is small, resulting in a low optimized capacity. Since dramatic improvements in both gravimetric and volumetric capacities are needed to meet the Department of Energy targets at 35 bar and ambient temperature, increasing capacity must be the primary focus of materials development efforts, but these efforts will be most beneficial if the binding enthalpy is near optimal.
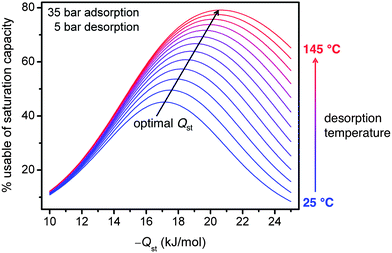 | ||
| Fig. 7 Assuming a single-site Langmuir isotherm, the percentage of the saturation capacity that is usable is plotted for isosteric heats of adsorption, Qst, ranging from −10 to −25 kJ mol−1 and desorption temperatures from 25 to 145 °C, with adsorption at 35 bar, desorption at 5 bar, and a molar entropy of adsorption of −9.5 R. As the desorption temperature increases, the optimal Qst and usable capacity also increase.65 | ||
Relative importance of gravimetric and volumetric capacity
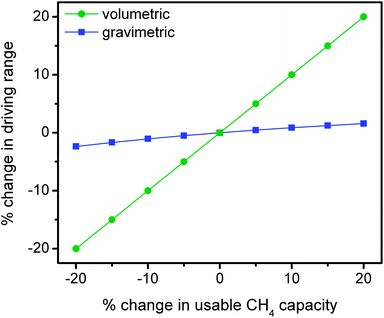
It is important to recognize that the acceptability and viability of natural gas vehicles are directly linked to their utility and value to the customer. As indicated, the lower volumetric energy density of compressed natural gas significantly reduces the driving range in comparison to conventional gasoline vehicles and therefore reduces the utility of the vehicle. In designing a next generation of adsorbents for natural gas storage, it is essential to consider the relative importance of improvements in gravimetric versus volumetric usable capacity toward increasing the maximum achievable driving range of an ANG vehicle.In order to make the comparison more informative, the effects of changes in gravimetric and volumetric usable capacity on driving range are considered independently using a few simple assumptions (Fig. 8). In the gravimetric case, a 10 GGE (gallons gasoline equivalent) vehicle is assumed to have an adsorbent capable of delivering 0.12 gCH4 g−1, which is equal to the usable capacity of HKUST-1 for 35 bar adsorption and 5 bar desorption at 25 °C. In order to isolate the effects of changing the usable gravimetric capacity, this analysis assumes a fixed volumetric capacity and changes in gravimetric capacity thus lead to an increase or decrease in the weight of adsorbent required to achieve a 10 GGE energy density (2.567 kg CH4).67 As a general rule, the fuel economy on conventional light-duty vehicles can be improved or reduced by up to 2% per 100 lbs (45 kg) of weight subtracted or added.68 Since the total amount of natural gas is fixed, changes in the fuel economy are directly proportional to changes in the driving range for this scenario. For example, a 10% improvement in the usable gravimetric capacity of HKUST-1 results in a 19 kg reduction in weight and a 0.8% improvement in fuel economy and driving range.
To isolate the effects of changing usable volumetric capacity, it is assumed that a light-duty vehicle will have a fixed amount of space available for a fuel tank. As a result, there is a roughly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correlation between the usable volumetric capacity of an adsorbent and the expected driving range of a vehicle.
1 correlation between the usable volumetric capacity of an adsorbent and the expected driving range of a vehicle.
As shown in Fig. 8, improvements in gravimetric capacity have considerably less impact than improvements in volumetric capacity. While increases in gravimetric capacity are still important, similar improvement percentages do not have as significant an impact as volumetric on increasing driving range since the increased weight of the adsorbent material has a minor effect on the fuel economy of the vehicle. Therefore, increasing the usable volumetric CH4 capacity is significantly more important than increasing the usable gravimetric capacity for natural gas storage in light-duty vehicles.
These relationships, along with knowledge of the importance of certain vehicle attributes to consumers, such as driving range and cost, are critical for directing adsorbent material improvements and tradeoffs toward the optimal solution for a viable ANG system.
Adsorbed natural gas system requirements
While working to synthesize a next generation of metal–organic frameworks with improved volumetric and gravimetric capacities, it is also important to consider the complete ANG storage system, as there are several factors that can dramatically affect the ultimate performance of a material when delivering natural gas to an engine. It is worth nothing that many of these systems-level issues are not just engineering problems and are fundamentally related to materials properties that can potentially be tuned through synthetic chemistry to improve performance.Thermal properties
In an actual ANG system, the heats of adsorption (exothermic) and desorption (endothermic) will likely lead to large temperatures changes that both have a negative impact on the usable CH4 capacity.69 Specifically, an adsorbent bed will release heat during refueling and cool during discharge, resulting in less CH4 stored during adsorption and more retained during desorption. Faster refueling and discharge rates, which are often desirable, lead to even greater temperature changes. Indeed, a prototype activated carbon storage tank cooled by as much as 37 °C at a discharge rate typical for a normal driving speed, resulting in a 20% loss in CH4 capacity compared to isothermal desorption.69 Various thermal management strategies have been proposed to minimize the impacts of heat flowing in and out of the adsorbent bed, including incorporating a heat exchanger inside the storage tank, changing how natural gas flows inside the tank, and altering the material and geometry of the tank.13,69,70 While some form of thermal management will ultimately be necessary, all of these engineering solutions involve a significant tradeoff between cost, weight, and available space.More importantly, all efforts to manage heat flow are highly dependent on the heat capacity and thermal conductivity of the adsorbent. High heat capacities decrease the magnitude of temperature changes resulting from the energy released or consumed during adsorption and desorption, while high thermal conductivities allow heat to dissipate more quickly and permit the use of simpler external or internal temperature control systems. With this in mind, it is worth noting that overcoming thermal management challenges is not just an engineering problem, and there can be a significant contribution from a more fundamental materials synthesis perspective.
While heat capacities have been reported for several metal–organic frameworks,41o,71 to the best of our knowledge, there have been just two thermal conductivity measurements, both of which were for MOF-5.72 As is typical of many porous materials, the MOF-5 thermal conductivities were very low at less than 0.32 W m−1 K−1 for both a single crystal and packed powder. It is possible to improve the thermal conductivity by incorporating an additive such as graphite, but this will lead to a decrease in both the gravimetric and volumetric CH4 capacities.72b To better understand these tradeoffs, there is a clear need for thermal conductivity and heat capacity measurements on a much wider range of metal–organic frameworks, especially with experiments designed to identify structural and chemical features that are likely to lead to frameworks with higher intrinsic thermal conductivities and heat capacities.
Mechanical properties
As has been emphasized, the volumetric CH4 capacity of an adsorbent has a critical impact on the ultimate driving range of an ANG vehicle. Notably, almost all reported volumetric uptakes for metal–organic frameworks, including those in this study, are calculated using the density of a perfect single crystal and represent the maximum possible volumetric capacity. In reality, metal–organic frameworks synthesized on a large enough scale to fill a fuel tank will likely be powders that contain a significant amount of empty space between particles. This interparticle void space results in a much lower density, and consequently a lower volumetric CH4 capacity, for a bulk powder than that calculated for a single crystal. Indeed, the bulk powder density of MOF-5 was measured at just 0.13 g cm−3, 79% less than the single crystal density of 0.621 g cm−3.73d Note that in addition to decreasing volumetric capacity, low packing densities also lead to lower thermal conductivities.In order to minimize the losses in capacity and thermal conductivity that result from packing adsorbent particles inside a tank, it will be essential to compact the material in some fashion. Compaction reduces the interparticle void space and increases the bulk density of the powder, but it can also cause partial or complete collapse of framework pores. As a result, materials with higher mechanical stability are desirable, as they are more likely to survive compaction to higher densities without significant losses in porosity. While there have been initial studies on the intrinsic mechanical properties of different metal–organic frameworks, the majority of work has been limited to frameworks that can be synthesized as large single crystals.74
Additional research efforts have examined changes in surface area, pore volume, and gas uptake when compacting different metal–organic framework powders, including MOF-5, HKUST-1, and Ni2(dobdc), at increasing mechanical pressures.43c,73 For instance, tablets of HKUST-1 compacted to 66% of its crystallographic density adsorbed just 94 v/v of CH4 at 35 bar and 30 °C,43c highlighting the importance of packing losses on the actual volumetric capacity of an adsorbent. Similarly, a pellet of Ni2(dobdc) compacted with 0.1 GPa of pressure adsorbed just 100 v/v of CH4 at 34 bar and 30 °C,73c significantly less than the 230 v/v measured here. These types of compaction studies are certainly useful, but it is difficult to compare the intrinsic mechanical properties of each material based on such measurements, since compaction is affected by particle size and shape in addition to mechanical stability. More importantly, comparisons of the volumetric usable capacity of different materials will be highly dependent on the mechanical stability of the framework and the maximum compaction density that can be achieved. Based on current work, the extent of varying degrees of mechanical stability between different metal–organic frameworks is poorly understood.
With this in mind, efforts to understand fundamental relationships between framework structure and mechanical properties will be extremely valuable in directing synthesis efforts toward robust materials that can be compacted to sufficiently high densities without structural changes that might affect CH4 adsorption capacities.75 Equally important will be research toward obtaining finer control over the size and morphology of metal–organic framework particles. In particular, studies on compacting activated carbons have demonstrated that significantly higher packing densities can be achieved when particles of two or more different sizes are mixed and compacted at the same time.7,76 To our knowledge, there have not yet been any studies evaluating the effects of the particle size distribution and shape on the achievable packing density for metal–organic frameworks. Note that in addition to evaluating changes in porosity upon compaction, it is also important to consider potential affects on the adsorption and desorption kinetics, as fast kinetics are important for achieving practical refueling and discharge rates in a vehicle.77
Natural gas impurities
Although CH4 is the largest component, pipeline-quality natural gas contains many other impurities that can affect the long-term stability and capacity of an adsorbent (Table 3).78 In an ANG vehicle, a guard bed will likely be placed before the storage tank during refueling to minimize exposure to impurities.20 Still, the adsorbent will inevitably be exposed to at least some level of each impurity throughout its lifetime. Additionally, most guard beds are unlikely to remove a significant amount of the C2 and C3 hydrocarbons that are present in natural gas, and it is unclear how this might affect the usable CH4 capacity of an adsorbent. Smaller levels of other impurities, especially sulfur-containing compounds, H2O, O2, and C4 and greater hydrocarbons, may slowly poison CH4 adsorption sites or degrade the framework over an extended time period. Performing cycling studies in the presence of all expected natural gas impurities will be critical to designing metal–organic frameworks with the long lifetimes necessary for use in a natural gas powered vehicle.| Chemical formulaa | Common name | ρ cryst (g cm−3) | V p (cm3 g−1) | Surface area (m2 g−1) | Total CH4 adsorptionb | P (bar) | T (°C) | Ref. | ||
|---|---|---|---|---|---|---|---|---|---|---|
| BET | Langmuir | cm3STP cm−3 | cm3STP g−1 | |||||||
| a adip = 5,5′-(9,10-anthracenediyl)di-isophthalate; azpy = 4,4′-azopyridine; bbc = 4,4′,4′′-[benzene-1,3,5-triyl-tris(benzene-4,1-diyl)]tribenzoate; bbcdc = 9,9′-([1,1′-biphenyl]-4,4′-diyl)bis(9H-carbazole-3,6-dicarboxylate); bdc = 1,4-benzenedicarboxylate; bdcppi = N,N′-bis(3,5-dicarboxyphenyl)pyromellitic diimide; bdi = 5,5′-(buta-1,3-diyne-1,4-diyl)diisophthalate; bdpp = 3,5-bis(3,5-dicarboxylphenyl)-pyridine; BenzTB = N,N,N′,N′-benzidinetetrabenzoate; bhb = 3,3′,3′′,5,5′,5′′-benzene-1,3,5-triyl-hexabenzoate; bpdc = biphenyldicarboxylate; bpta = 3,6-di(4-pyridyl)-1,2,4,5-tetrazine; bptc = biphenyl-3,3′,5,5′-tetracarboxylate; 4,4′-bpy = 4,4′-bipyridine; bpydb = 4,4′-(4,4′-bipyridine-2,6-diyl)dibenzoate; btb = benzene-1,3,5-tribenzoate; btc = 1,3,5-benzenetricarboxylate; bte = 4,4′,4′′-[benzene-1,3,5-triyl-tris (ethyne-2,1-diyl)]tribenzoate; btei = 5,5′,5′′-benzene-1,3,5-triyltris(1-ethynyl-2-isophthalate); bttdc = 9,9′,9′′,9′′′-([1,1′-biphenyl]-3,3′,5,5′-tetrayl)tetrakis(9H-carbazole-3,6-dicarboxylate); cbIM = b-chlorobenzoimidazole; ceb = 4-(2-carboxyethyl)benzoate; cvb = 4-(2-carboxyvinyl)benzoate; dabco = 1,4-diazabicyclo[2.2.2]octane; dceni = 6,6′-dichloro-2,2′-diethoxy-1,1′-binaphthyl-4,4′-di(5-isophthalate); dhbc = 2,5-dihydroxybenzoate; dobdc = 2,5-dioxido-1,4-benzenedicarboxylate; ebdc = 5,5′-(1,2-ethynediyl)bis(1,3-benzenedicarboxylate); fddi = tetramethyl 5,5′-(9H-flourene-2,7-diyl)diisophthalate acid; H2tbcppm = {3,5-bis[(4-carboxyl)phenyl]phenyl}methane; iBu-stpdc = 4,4′,4′′-(isobutylsilanetriyl)tris-(triphenyl-3,5-dicarboxylate); Im = imidazole; Me-stpdc = 4,4′,4′′-(methylsilanetriyl)tris-(triphenyl-3,5-dicarboxylate); MeIM = 2-methylimidazole; ndc = 2,6-naphthalenedicarboxylate; 2,7-ndc = 2,7-naphthalenedicarboxylate; 1,4-nddi = 5,5′-naphthalene-1,4-diyl-diisophthalate; 2,6-nddi = 5,5′-naphthalene-2,6-diyl-diisophthalate; NH2-bdc = 2-amino-1,4-benzenedicarboxylate; ntei = 5,5′,5′′-(4,4′,4′′-nitrilotris(benzene-4,1-diyl)tris(ethyne-2,1-diyl))triisophthalate; OH-stpdc = 4,4′,4′′-(hydroxysilanetriyl)tris-(triphenyl-3,5-dicarboxylate); pddi = 5,5′-(pyridine-2,5-diyl)diisophthalate; ptei = 5,5′-((5′-(4-((3,5-dicarboxyphenyl)ethynyl)phenyl)-[1,1′,3′,1′′-terphenyl]-4,4′′-diyl)-bis(ethyne-2,1-diyl))diisophthalic acid; qptc = quaterphenyl-3,3′′′,5,5′′′-tetracarboxylate; sbtc = trans-stilbene-3,3′,5,5′-tetracarboxylate; tcbpa = tris(4′-carboxy-biphenyl)amine; tcepbb = 1,3,5-tris[(1,3-carboxylate-5-(4-(ethynyl)phenyl))butadiynyl]-benzene; tcpbda = N,N,N′,N′-tetrakis(4-carboxylphenyl)biphenyl-4,4′-diamine; tdpat = 2,4,6-tris(3,5-dicarboxylphenylamino)-1,3,5-triazine; ted = triethylenediamine; tipb = 1,2,4,5-tetra(5-isophthalate)benzene; tptc = terphenyl-3,3′,5,5′-tetracarboxylate. b Values were extrapolated from adsorption isotherms when not explicitly stated in the text or ESI. Excess adsorption was converted to total using reported pore volumes and the bulk CH4 density from the NIST REFPROP database. c This is the real, measured density of the pellet. Note that the pellet contains 2% Alox C and 3% graphite as additives. d Not specified whether uptake is in terms of excess, total or absolute adsorption. Consequently, values are simply reproduced from original publication and not converted. e Pore volume was taken from this work to calculate total adsorption. f Structure of framework during CH4 adsorption is uncertain, and volumetric adsorption cannot be reasonably estimated. Also, it is not specified whether uptake is in terms of excess, total or absolute adsorption. | ||||||||||
| Ni2(dobdc) | Ni-MOF-74, CPO-27-Ni | 1.195 | 0.56 | 1593 | 230 | 193 | 35 | 25 | This work | |
| 0.47 | 1218 | 214 | 179 | 35 | 25 | 41h | ||||
| 0.44 | 1027 | 206 | 172 | 35 | 25 | 42 | ||||
| Cu3(btc)2 | HKUST-1 | 0.881 | 0.77 | 2203 | 225 | 255 | 35 | 25 | This work | |
| 0.75 | 1663 | 220 | 250 | 35 | 22 | 43e | ||||
| 0.67 | 1850 | 217 | 246 | 35 | 30 | 43g | ||||
| 0.76 | 1502 | 2216 | 198 | 225 | 35 | 30 | 43b | |||
| 0.71 | 1555 | 194 | 221 | 35 | 30 | 43d | ||||
| 0.72 | 184 | 209 | 35 | 30 | 44b | |||||
| HKUST-1 tablet (3 × 3 mm) | 0.582c | 94d | 162d | 35 | 30 | 43c | ||||
| Co2(dobdc) | Co-MOF-74, CPO-27-Co | 1.173 | 0.51 | 1433 | 221 | 188 | 35 | 25 | This work | |
| 0.48 | 1056 | 194 | 165 | 35 | 25 | 42 | ||||
| Cu2(adip) | PCN-14 | 0.829 | 0.83 | 1984 | 2360 | 202 | 244 | 35 | 25 | This work |
| 0.87 | 1753 | 2176 | 235 | 283 | 35 | 17 | 45a | |||
| Mg2(dobdc) | Mg-MOF-74, CPO-27-Mg | 0.909 | 0.69 | 1957 | 200 | 220 | 35 | 25 | This work | |
| 0.63 | 1542 | 188 | 207 | 35 | 25 | 41h | ||||
| 0.61 | 1332 | 168 | 184 | 35 | 25 | 42 | ||||
| Cu2(bdpp) | NJU-Bai10 | 0.668 | 1.11 | 2883 | 3108 | 197 | 296 | 35 | 17 | 80 |
| Cu2(1,4-nddi) | NOTT-109 | 0.790 | 0.85 | 2110 | 197 | 250 | 35 | 27 | 61 | |
| Zn(bdc)(ted)0.5 | 0.893 | 0.65 | 1794 | 2015 | 197d | 221d | 35 | 25 | 81 | |
| Cu3(bdb) | UTSA-20 | 0.91 | 0.63 | 1156 | 197 | 217 | 35 | 27 | 82 | |
| Cu2(tptc) | NOTT-101 | 0.684 | 1.08 | 2805 | 196 | 286 | 35 | 27 | 61 | |
| Cu2(sbtc) | PCN-11 | 0.749 | 0.91 | 1931 | 2442 | 194 | 259 | 35 | 25 | 83 |
| Cu2(bptc) | NOTT-100, MOF-505 | 0.927 | 0.677 | 1661 | 194 | 209 | 35 | 27 | 61 | |
| Cu2(2,6-nddi) | NOTT-103 | 0.643 | 1.157 | 2958 | 194 | 301 | 35 | 27 | 61 | |
| [Zn3(OH)]4(tbcppm)(H2tbcppm)2 | 0.685 | 1.14 | 2718 | 3120 | 194 | 283 | 35 | 25 | 84 | |
| Cu2(ebdc) | PCN-16 | 0.724 | 1.06 | 2273 | 2800 | 192 | 265 | 35 | 27 | 85 |
| Cu2(C26H20O8) | NOTT-107 | 0.756 | 0.767 | 1770 | 191 | 252 | 35 | 25 | 24h and 86 | |
| Cu2(pddi) | ZJU-5 | 0.679 | 1.074 | 2823 | 190 | 280 | 35 | 27 | 87 | |
| Zn2(dobdc) | Zn-MOF-74 | 1.231 | 0.41 | 885 | 188 | 153 | 35 | 25 | 42 | |
| Al(OH)(bdc) | MIL-53 (Al) | 0.978 | 0.54 | 1235 | 1627 | 186d | 190d | 35 | 30 | 88 |
| 0.54 | 1140 | 1590 | 155 | 159 | 35 | 31 | 89 and 90 | |||
| 0.56 | 121 | 124 | 35 | 30 | 91 | |||||
| Cu3(tdpat) | 0.782 | 0.93 | 1938 | 2608 | 182 | 232 | 35 | 25 | 50 | |
| Cu2(qptc) | NOTT-102 | 0.587 | 1.268 | 3342 | 181 | 308 | 35 | 27 | 61 | |
| Cu2(fddi) | ZJU-25 | 0.622 | 1.18 | 2125 | 3304 | 180 | 289 | 35 | 27 | 92 |
| Cu3[(C6H3)(C2N3H)3(C6H3)3(COO)6] | NU-125 | 0.578 | 1.29 | 3120 | 179 | 310 | 35 | 25 | 93 | |
| Zn4O(C2H4-bdc)3 | IRMOF-6 | 0.65 | 0.92 | 2630 | 177 | 272 | 36.5 | 25 | 94 | |
| Mn2(dobdc) | Mn-MOF-74 | 1.084 | 0.5 | 1102 | 176 | 163 | 35 | 25 | 42 | |
| Zn2(bdc)2(dabco) | 0.822 | 0.75 | 1448 | 2104 | 164 | 199 | 35 | 30 | 43b | |
| 0.68 | 1450 | 159 | 194 | 35 | 23 | 95 | ||||
| Cu3(OH-stpdc) | SDU-6 | 0.611 | 1.17 | 2826 | 172 | 281 | 35 | 25 | 96 | |
| Cu3(btei) | PCN-61 | 0.56 | 1.36 | 3000 | 3500 | 171 | 306 | 35 | 25 | 97 |
| Cu2(bdi) | PCN-46 | 0.619 | 1.012 | 2500 | 2800 | 171 | 277 | 35 | 25 | 98 |
| Zn4O(bdc)3 | IRMOF-1, MOF-5 | 0.621 | 1.4e | 168 | 271 | 36.5 | 25 | 23a | ||
| 1.4 | 3995 | 150 | 241 | 35 | 25 | This work | ||||
| 1.2 | 143 | 230 | 36 | 27 | 39 | |||||
| 1.55 | 3800 | 4400 | 138 | 223 | 35 | 25 | 46d | |||
| Zr6O4(OH)4(NH2-bdc)6 | UiO-66-NH2 | 1.36 | 0.4 | 1080 | 167 | 123 | 35 | 30 | 43g | |
| Cr(OH)(bdc) | MIL-53 (Cr) | 1.04 | 0.5 | 1500 | 165 | 159 | 35 | 31 | 89 | |
| Co2(bdc)2(dabco) | 0.815 | 0.82 | 1600 | 2300 | 161 | 197 | 35 | 30 | 99 | |
| Cu3(Me-stpdc) | SDU-7 | 0.605 | 1.1 | 2713 | 159 | 263 | 35 | 25 | 96 | |
| Cu3(tipb) | UTSA-34 | 0.84 | 0.542 | 991 | 159 | 189 | 35 | 17 | 100 | |
| Cu2(dceni) | UTSA-40 | 0.827 | 0.65 | 1630 | 1661 | 152 | 184 | 35 | 27 | 101 |
| Cu2(ndc)2(dabco) | DUT-8 (Cu) | 0.681 | 1.04 | 2535 | 148 | 217 | 35 | 25 | 102 | |
| Cu2(bttcd) | PCN-80 | 0.575 | 1.47 | 3850 | 4150 | 147 | 255 | 35 | 23 | 103 |
| Zn4O(tcbpa)2 | SNU-77 | 0.586 | 1.52 | 3670 | 4180 | 147 | 250 | 35 | 25 | 104 |
| Cu3(iBu-stpdc) | SDU-8 | 0.613 | 1.02 | 2516 | 146 | 238 | 35 | 25 | 105 | |
| Zr6O4(OH)4(bdc)6 | UiO-66 | 1.32 | 0.36 | 970 | 146 | 110 | 35 | 30 | 43g | |
| Zn4O(NH2-bdc)3 | IRMOF-3 | 0.63 | 1.07 | 144 | 228 | 36.5 | 25 | 23a and 106 | ||
| Ti8O8(OH)4(bdc)6 | MIL-125 | 0.81 | 0.67 | 1820 | 141 | 174 | 35 | 30 | 43g | |
| Yb3O[(C6H3)4(C6H4)6(COO)6](NO3) | UTSA-62 | 0.59 | 0.91 | 2190 | 139 | 236 | 35 | 25 | 107 | |
| Cu3(tcepbb) | NU-111 | 0.409 | 2.09 | 4930 | 136 | 333 | 35 | 25 | 49 | |
| Cu3(ntei) | PCN-66 | 0.44 | 1.63 | 4000 | 4600 | 134 | 304 | 35 | 25 | 108 |
| Co2(bipy)3(btb)4 | DUT-23 (Co) | 0.401 | 2.03 | 4850 | 133 | 331 | 35 | 25 | 109 | |
| Zn(MeIM)2 | ZIF-8 | 1.141 | 0.49 | 131 | 115 | 36 | 27 | 39 | ||
| 0.59 | 1445 | 124 | 109 | 35 | 30 | 110 | ||||
| Zn4O(ceb)3 | SNU-71 | 0.835 | 0.709 | 1770 | 1923 | 130 | 155 | 35 | 25 | 111 |
| Ni(ndc)(ted)0.5 | 0.789 | 0.84 | 2307 | 2647 | 128d | 162d | 35 | 25 | 81 | |
| Cu3(ptei) | PCN-68 | 0.38 | 2.13 | 5109 | 6033 | 126 | 332 | 35 | 25 | 97 |
| Zn4O(btb)2 | MOF-177 | 0.427 | 1.89 | 4500 | 5340 | 126 | 293 | 35 | 25 | 46d |
| 1.55 | 106 | 249 | 35 | 25 | 112 | |||||
| Cu(SiF6)(4,4′-bpy)2 | 0.86 | 1337 | 125 | 146 | 36.5 | 25 | 113 | |||
| 0.56 | 1337 | 124 | 144 | 35 | 25 | 114 | ||||
| Zn3O(2,7-ndc)2 | 1.04 | 0.458 | 901 | 1281 | 125 | 120 | 35 | 25 | 115 | |
| Cu(GeF6)(4,4′-bpy)2 | 0.925 | 124 | 134 | 36.5 | 25 | 113 | ||||
| Cu2(bdcppi) | SNU-50 | 0.65 | 1.08 | 2300 | 2450 | 123 | 189 | 35 | 25 | 116 |
| Al(OH)(ndc) | DUT-4 | 0.773 | 0.68 | 1308 | 1996 | 122 | 158 | 35 | 30 | 117 |
| Zn4O(ndc)3 | UTSA-38 | 0.962 | 0.61 | 1090 | 1690 | 120d | 124d | 35 | 27 | 118 |
| Cr3O(btc)2F | MIL-100 (Cr) | 0.7 | 1.1 | 1900 | 120 | 171 | 35 | 30 | 119 | |
| Zn4O(btb)4/3(ndc) | MOF-205 | 0.38 | 2.16 | 4460 | 6170 | 119 | 314 | 35 | 25 | 46d |
| Zn4O(ndc)3 | IRMOF-8 | 0.448 | 1.827 | 4326 | 114 | 254 | 35 | 25 | 120 | |
| Zn4O(btb)4/3(ndc) | DUT-6 | 0.39 | 2.02 | 6005 | 106 | 271 | 35 | 25 | 121 | |
| Fe3O(btc)2F | MIL-100 (Fe) | 0.7 | 0.99 | 2410 | 117 | 167 | 35 | 30 | 43g | |
| Al(OH)(bpdc) | DUT-5 | 0.634 | 0.81 | 1613 | 2335 | 113 | 179 | 35 | 30 | 117 |
| Cu2(bbcdc) | DUT-49 | 0.311 | 2.91 | 5476 | 113 | 363 | 35 | 25 | 48 | |
| Zn4O(cvb)3 | SNU-70 | 0.408 | 2.17 | 5290 | 6100 | 111 | 273 | 35 | 25 | 122 |
| Zn6(btb)4(4,4′-bpy)3 | FJI-1 | 0.405 | 1.43 | 4043 | 4624 | 111 | 273 | 35 | 25 | 123 |
| Zn(Im)1.5(cbIM)0.5 | ZIF-76 | 0.869 | 0.57 | 1340 | 110 | 126 | 35 | 30 | 124 | |
| Cu3(C66H36O12) | NOTT-119 | 0.361 | 2.35 | 4118 | 106 | 294 | 35 | 25 | 125 | |
| Cd(bpydb) | 1.21 | 0.35 | 346 | 104 | 86 | 35 | 25 | 126 | ||
| Ni5O2(btb)2 | DUT-9 | 0.358 | 2.18 | 6120 | 101 | 283 | 35 | 25 | 127 | |
| Cr3O(bdc)3F | MIL-101 (Cr) | 0.44 | 2.15 | 4230 | 101 | 230 | 35 | 30 | 119 | |
| 1.57 | 3870 | 87 | 197 | 35 | 30 | 43g | ||||
| 1.38 | 2674 | 82 | 186 | 35 | 22 | 43e | ||||
| 1.303 | 2693 | 4492 | 79 | 178 | 35 | 30 | 43b | |||
| Zn4O(BenzTB)3/2 | DUT-13 | 0.385 | 1.98 | 5570 | 96 | 250 | 35 | 25 | 128 | |
| Zn4O(bte)4/3(bpdc) | MOF-210 | 0.25 | 3.6 | 6240 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
83 | 331 | 35 | 25 | 46d |
| Co2(4,4′-bpy)3(NO3)4 | 1.36 | 73 | 54 | 35 | 25 | 23 | ||||
| Zn4O(bbc)2 | MOF-200 | 0.22 | 3.59 | 4530 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
67 | 304 | 35 | 25 | 46d |
| Cd2(azpy)3(NO3)4 | 1.54 | 66 | 43 | 36.5 | 25 | 129 | ||||
| Co2(ndc)2(dabco) | DUT-8 (Co) | 0.67 | 0.62 | 1400 | 52 | 78 | 35 | 25 | 102 | |
| Zn2(ndc)2(dabco) | DUT-8 (Zn) | 0.68 | 0.3 | 710 | 40 | 59 | 35 | 25 | 102 | |
| Cu2(PF6)(NO3)(4,4′-bpy)4·1.4PF6·0.6NO3 | 1.057 | 559 | 33 | 31 | 36.5 | 25 | 113 | |||
| Zn2(tcpbda) | SNU-30 | 0.381 | 0.28 | 704 | 770 | 27 | 71 | 35 | 25 | 130 |
| Co(azpy)2(NCS)2 | 1.31 | 19 | 15 | 35.5 | 25 | 129 | ||||
| Co2(azpy)3(NO3)4 | 1.32 | 17 | 13 | 36.5 | 25 | 129 | ||||
| Zn2(tcpbda)(bpta) | SNU-31 | 0.459 | 0.14 | 308 | 17 | 37 | 35 | 25 | 130 | |
| Cu(C10H6O4)(ted)0.5 | 1.08 | 3129 | 214f | 35 | 25 | 131 | ||||
| Cu(bpdc)(ted)0.5 | 1.27 | 3265 | 213f | 35 | 25 | 131 | ||||
| Cu(bdc)(ted)0.5 | 0.71 | 1891 | 185f | 35 | 25 | 131b | ||||
| VO(bdc) | MIL-47 (V) | 0.5 | 1030 | 137f | 35 | 30 | 132 | |||
| Cu(C4H2O4)(ted)0.5 | 0.24 | 606 | 103f | 35 | 25 | 131b | ||||
| Cu(dhbc)2(4,4′-bpy) | 320 | 70f | 35 | 25 | 133 | |||||
| AX-21 activated carbon | 0.49 | 1.64 | 4880 | 154 | 315 | 35 | 25 | this work | ||
| C25H24B4O8 | COF-102 | 0.43 | 1.55 | 3620 | 4650 | 135 | 313 | 35 | 25 | 134 |
| C99H64Si4 | PPN-4 | 0.284 | 3.04 | 6461 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 063 063 |
109 | 384 | 35 | 25 | 135 |
| Na86[(AlO2)86(SiO2)106] | Zeolite NaX | 1.43 | 0.27 | 106 | 74 | 35.5 | 25 | 136 | ||
| Na12[(AlO2)12(SiO2)12] | Zeolite 5A | 1.48 | 0.2 | 104 | 70 | 35.5 | 5 | 136 | ||
| Component | Mol.% |
|---|---|
| CH4 | 87–96 |
| C2H6 | 1.5–5.1 |
| C3 or greater hydrocarbons | 0.1–2.3 |
| C6 or greater hydrocarbons | <0.1 |
| N2 | 0.7–5.6 |
| CO2 | 0.1–1.0 |
| O2 | <0.1 |
| H2 | <0.02 |
| H2O | <80 mg m−3 |
| Sulfur (including odorants) | 5.5 mg m−3 |
Conclusions
With some of the highest volumetric and gravimetric CH4 capacities ever reported, metal–organic frameworks have shown significant potential as adsorbents for natural gas storage. There are still, however, some formidable challenges to overcome before they are likely to find widespread use in natural gas vehicles. Most importantly, substantial increases in the usable volumetric capacity are needed for improving the driving range to levels closer to that of gasoline vehicles. To go beyond just incremental improvements in capacity, completely new design strategies will likely be necessary. For instance, new types of strong binding sites that occupy a small volume but can each polarize multiple CH4 molecules should dramatically increase the volumetric density of stored CH4. Above all, any efforts to minimize the amount of wasted volume inside frameworks that does not contribute to optimally attracting CH4 molecules, without significantly decreasing porosity, should be beneficial. This includes extra empty space inside large pores, as well as adsorption sites on the pore surface that are too weak or too strong for maximizing the usable capacity.It is important to emphasize that efforts to design a next generation of high-capacity metal–organic frameworks for natural gas storage must address systems-level factors that will heavily influence the actual performance of a material, including compaction, heat capacity, thermal conductivity, and tolerance to impurities. Studies that address these areas are not only important for determining the practically achievable usable capacity and lifetime of different materials, but improving our fundamental understanding of the relationship of framework structure and chemical composition with thermal properties, mechanical properties, and long-term stability will also help guide synthetic efforts toward the most useful materials. Ultimately, the cost of the material will also be an important factor in determining the competitiveness of an ANG vehicle. While it is difficult to predict the large-scale cost of organic ligands for which there are currently little demand, basic economic analyses of the best current metal–organic frameworks would be useful for identifying strategies to target materials with the greatest potential for scale-up to the levels required to have an impact in natural gas vehicles.
Acknowledgements
This research was funded by the Advanced Research Projects Agency – Energy (ARPA-E), U.S. Department of Energy. We thank Dr Bruce Hardy, Dr Donald Anton, Michael SantaMaria, Dr Bill Dolan, Dr Lena Arnold, Dr Stefan Marx, and Dr Dane Boysen for helpful discussions. We also thank NSF for providing graduate fellowship support for J.A.M.Notes and references
- A. Celzard and V. Fierro, Energy Fuels, 2005, 19, 573 CrossRef CAS.
- (a) O. Talu, Proc. IVth Int. Conf. on Fundamentals of Adsorption, Kyoto, 1992, p. 655 Search PubMed; (b) D. Lozanao-Castelló, J. Alcañiz-Monge, M. A. de la Casa-Lillo, D. Cazorla-Amorós and A. Linares-Solano, Fuel, 2002, 81, 1777 CrossRef.
- C. F. Blazek, J. Grimes, P. Freman, B. K. Bailey and C. Colucci, Prepr. Pap. - Am. Chem. Soc., Div. Fuel Chem., 1994, 39, 476 CAS.
- International Energy Agency, World Energy Outlook 2011: Are We Entering a Golden Age of Gas, http://www.worldenergyoutlook.org Search PubMed.
- Alternative Fuels Data Center – Fuel Properties Comparison, 2013, http://www.afdc.energy.gov/fuels/fuel_comparison_chart.pdf Search PubMed.
- (a) S. Yeh, Energy Policy, 2007, 35, 5865 CrossRef; (b) G. A. Whyatt, Issues Affecting Adoption of Natural Gas in Light- and Heavy-Duty Vehicles, 2010, PNNL-19745 Search PubMed.
- V. C. Menon and S. Komarneni, J. Porous Mater., 1998, 5, 43 CrossRef CAS.
- (a) E. W. Lemmon, M. L. Huber and M. O. McLinden, NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 8.0, National Institute of Standards and Technology, Standard Reference Data Program, Gaithersburg, 2007 Search PubMed; (b) U. Setzmann and W. Wagner, J. Phys. Chem. Ref. Data, 1991, 20, 1061 CrossRef CAS.
- D. W. Breck, Zeolite Molecular Sieves, J. Wiley & Sons, New York, 1974 Search PubMed.
- (a) R. A. Munson and R. A. Clifton, Jr., Natural Gas Storage with Zeolites, U.S. Dept. of the Interior, 1971 Search PubMed; (b) R. F. Cracknell, P. Gordon and K. E. Gubbins, J. Phys. Chem., 1993, 97, 494 CrossRef CAS.
- J. Wegrzyn and M. Gurevich, Appl. Energy, 1996, 55, 71 CrossRef CAS.
- (a) R. W. Judd, D. T. M. Gladding, R. C. Hodrien, D. R. Bates, J. P. Ingram and M. Allen, Prepr. Pap. - Am. Chem. Soc., Div. Fuel Chem., 1998, 43, 575 CAS; (b) K. Dvorak and R. C. Hodrien, Development of Adsorbed Natural Gas Technology for Large Scale Diurnal Storage Applications, Int. Gas Research Conference, Amsterdam, 2001 Search PubMed; (c) L. Y. Lau and R. Judd, New Approach to Natural Gas Storage – Advances in Adsorbed Natural Gas (ANG) Technology, Int. Gas Research Conference, Paris, 2008 Search PubMed.
- N. D. Parkyns and D. F. Quinn, in Porosity in Carbons, ed. J. W. Patrick, Edward Arnold, London, 1995, ch. 11 Search PubMed.
- K. R. Matranga, A. L. Myers and E. D. Glandt, Chem. Eng. Sci., 1992, 47, 569 CrossRef.
- Note that 11.4 Å pores, which can accommodate 3 layers of CH4, are optimal for maximizing the amount of usable CH4 for adsorption near 35 bar and desorption near 1 bar.
- D. F. Quinn, J. A. MacDonald and K. Sosin, Prepr. Pap. - Am. Chem. Soc., Div. Fuel Chem., 1994, 39, 451 CAS.
- P. Pfeifer, et al. , Chaos, 2007, 17 Search PubMed 041108.
- The unit cm3STP is defined as the volume occupied by an ideal gas at a standard temperature and pressure (STP). Here, STP is defined as 273.15 K and 1 atm, resulting in a volume of 22.414 mL for 1 mmol of ideal gas at STP.
- Methane Opportunities for Vehicular Energy, Advanced Research Project Agency – Energy, U.S. Dept. of Energy, Funding Opportunity no. DE-FOA-0000672, 2012.
- T. L. Cook, C. Komodromos, D. F. Quinn and S. Ragan, Carbon Materials for Advanced Technologies, ed. T. D. Burchell, Elsevier, Amsterdam, 1999, ch. 9 Search PubMed.
- (a) H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 1999, 402, 276 CAS; (b) S. Kitagawa, R. Kitaura and S.-I. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334 CrossRef CAS PubMed; (c) R. Matsuda, R. Kitaura, S. Kitagawa, Y. Kubota, R. V. Belosludov, T. C. Kobayashi, H. Sakamoto, T. Chiba, M. Takata, Y. Kawazoe and Y. Mita, Nature, 2005, 436, 238 CrossRef CAS PubMed; (d) A. R. Millward and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 17998 CrossRef CAS PubMed; (e) G. Férey, Chem. Soc. Rev., 2008, 37, 191 RSC; (f) R. E. Morris and P. S. Wheatley, Angew. Chem., Int. Ed., 2008, 47, 4966 CrossRef CAS PubMed; (g) A. U. Czaja, N. Trukhan and U. Müller, Chem. Soc. Rev., 2009, 38, 1284 RSC; (h) B. Chen, S. Xiang and G. Qian, Acc. Chem. Res., 2010, 1115 CrossRef CAS PubMed; (i) H.-C. Zhou, J. R. Long and O. M. Yaghi, Chem. Rev., 2012, 112, 673 CrossRef CAS PubMed; (j) K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T.-H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724 CrossRef CAS PubMed; (k) J.-R. Li, J. Sculley and H.-C. Zhou, Chem. Rev., 2012, 112, 869 CrossRef CAS PubMed.
- (a) H. Furukawa, M. A. Miller and O. M. Yaghi, J. Mater. Chem., 2007, 17, 3197 RSC; (b) M. Dincă and J. R. Long, Angew. Chem., Int. Ed., 2008, 47, 6766 CrossRef PubMed; (c) L. J. Murray, M. Dincă and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294 RSC; (d) M. P. Suh, H. J. Park, T. K. Prasad and D.-W. Lim, Chem. Rev., 2012, 112, 782 CrossRef CAS PubMed.
- M. Kondo, T. Yoshitomi, K. Seki, H. Matsuzaka and S. Kitagawa, Angew. Chem., Int. Ed. Engl., 1997, 36, 1725 CrossRef CAS.
- (a) M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 295, 469 CrossRef CAS PubMed; (b) T. Düren, L. Sarkisov, O. M. Yaghi and R. Q. Snurr, Langmuir, 2004, 20, 2683 CrossRef; (c) W. Zhou, Chem. Rec., 2010, 10, 200 CrossRef CAS PubMed; (d) R. B. Getman, Y.-S. Bae, C. E. Wilmer and R. Q. Snurr, Chem. Rev., 2012, 112, 703 CrossRef CAS PubMed; (e) K. Konstas, T. Osl, Y. Yang, M. Batten, N. Burke, A. J. Hill and M. R. Hill, J. Mater. Chem., 2012, 22, 16698 RSC; (f) T. A. Makal, J.-R. Li, W. Lu and H.-C. Zhou, Chem. Soc. Rev., 2012, 41, 7761 RSC; (g) Y. He, W. Zhou, R. Krishna and B. Chen, Chem. Commun., 2012, 48, 11813 RSC; (h) C. E. Wilmer, M. Leaf, C. Yeon Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Nat. Chem., 2012, 4, 83 CrossRef CAS PubMed.
- J. W. Gibbs, The Collected Works of J. W. Gibbs, Longmans and Green, New York, 1928 Search PubMed.
- (a) S. Sircar, Ind. Eng. Chem. Res., 1999, 38, 3670 CrossRef CAS; (b) S. Sircar, AIChE J., 2001, 47, 1169 CrossRef CAS; (c) K. Murata, M. El-Merraoui and K. Kaneko, J. Chem. Phys., 2001, 114, 4196 CrossRef CAS; (d) A. L. Myers and P. A. Monson, Langmuir, 2002, 18, 10261 CrossRef CAS; (e) D. D. Do and H. D. Do, Carbon, 2003, 41, 1777 CrossRef CAS; (f) S. Gumma and O. Talu, Langmuir, 2010, 26, 17013 CrossRef CAS PubMed.
- While the total material adsorption is defined as the total number of gas molecules inside the pores of an adsorbent, the total system adsorption is defined as the total number of gas molecules inside the entire system, which includes interparticle voids and other empty spaces inside the adsorption vessel. Even though the total system adsorption is most important for application in a vehicle, total material adsorption is more meaningful for comparing properties of different adsorbents. In this work, the terms “total material adsorption” and “total adsorption” are used interchangeably.
- K. J. Gross, K. R. Carrington, S. Barcelo, A. Karkamkar, J. Purewal, S. Ma, H.-C. Zhou, P. Dantzer, K. Ott, T. Burrell, T. Semeslberger, Y. Pivak, B. Dam and D. Chandra, Recommended Best Practices for the Characterization of Storage Properties of Hydrogen Storage Materials, 2011, pp. V3–V5, U.S. D.O.E. Hydrogen Program document, http://www1.eere.energy.gov/hydrogenandfuelcells/pdfs/best_practices_hydrogen_storage.pdf Search PubMed.
- (a) M. Dincă, A. Dailly, Y. Liu, C. M. Brown, D. A. Neumann and J. R. Long, J. Am. Chem. Soc., 2006, 128, 16876 CrossRef PubMed; (b) E. Poirier and A. Dailly, J. Phys. Chem. C, 2008, 112, 13047 CrossRef CAS.
- For microporous materials, this is a particularly good approximation since most gas molecules inside a micropore should have some degree of interaction with the pore surface. As pores get larger, this may not always be a valid assumption, which can affect the accuracy of using isotherm data to calculate thermodynamic properties.
- K. S. W. Sing, D. H. Everett, R. A. W. Haul, L. Moscou, R. A. Pierotti, J. Rouquérol and T. Siemieniewska, Pure Appl. Chem., 1985, 57, 603 CrossRef CAS.
- L. Gurvich, J. Phys. Chem. Soc. Russ., 1915, 47, 805 CAS.
- More advanced techniques, such as t-Plots, the Horvath–Kawozoe (H–K) equation, and Density Functional Theory (DFT), can be used to extract detailed pore size distributions, but whether the calculated total pore volume from these methods will differ significantly from the simple single-point calculation using the Gurvich rule is not well studied.
- S. Lowell, J. Shields, M. A. Thomas and M. Thommes, Characterization of Porous Solids and Powders: Surface Area, Pore Size and Density, Springer, The Netherlands, 2004, pp. 111–112 Search PubMed.
- J. Moellmer, E. B. Celer, R. Luebke, A. J. Cairns, R. Staudt, M. Eddaoudi and M. Thommes, Microporous Mesoporous Mater., 2010, 129, 345 CrossRef CAS.
- R. Krishna, Microporous Mesoporous Mater., 2012, 156, 217 CrossRef CAS.
- (a) J. U. Keller, E. Robens and C. du Fresne von Hohenesche, Proc. COPS-VI, 2002, 144, 387 CAS; (b) Y. Belmabkhout, M. Frère and G. De Weireld, Meas. Sci. Technol., 2004, 15, 848 CrossRef CAS; (c) D. P. Broom, Int. J. Hydrogen Energy, 2007, 32, 4871 CrossRef CAS.
- P. Malbrunot, D. Vidal, J. Vermesse, R. Chahine and T. K. Bose, Langmuir, 1997, 13, 539 CrossRef CAS.
- W. Zhou, H. Wu, M. R. Hartman and T. Yildirim, J. Phys. Chem. C, 2007, 111, 16131 CAS.
- M. Kunowsky, F. Suárez-García and Á. Linares-Solano, Microporous Mesoporous Mater., 2013, 173, 47 CrossRef CAS.
- (a) N. L. Rosi, J. Kim, M. Eddaoudi, B. Chen, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 1504 CrossRef CAS PubMed; (b) S. R. Caskey, A. G. Wong-Foy and A. J. Matzger, J. Am. Chem. Soc., 2008, 130, 10870 CrossRef CAS PubMed; (c) P. D. C. Dietzel, R. Blom and H. Fjellvag, Eur. J. Inorg. Chem., 2008, 3624 CrossRef CAS; (d) Y. Liu, H. Kabbour, C. M. Brown, A. D. Neumann and C. C. Ahn, Langmuir, 2008, 24, 4772 CrossRef CAS PubMed; (e) P. D. C. Dietzel, R. E. Johnsen, H. Fjellvag, S. Bordiga, E. Groppo, S. Chavan and R. Blom, Chem. Commun., 2008, 5125 RSC; (f) W. Zhou, H. Wu and T. Yildirim, J. Am. Chem. Soc., 2008, 130, 15268 CrossRef CAS PubMed; (g) D. Britt, H. Furukawa, B. Wang, T. G. Glover and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 20637 CrossRef CAS PubMed; (h) P. D. C. Dietzel, V. Besikiotis and R. Blom, J. Mater. Chem., 2009, 19, 7362 RSC; (i) H. Wu, J. M. Simmons, G. Srinivas, W. Zhou and T. Yildirim, J. Phys. Chem. Lett., 2010, 1, 1946 CrossRef CAS; (j) L. Valenzano, B. Civalleri, S. Chavan, G. T. Palomino, C. O. Areán and S. Bordiga, J. Phys. Chem. C, 2010, 114, 11185 CrossRef CAS; (k) Z. Bao, L. Yu, Q. Ren, X. Lu and S. Deng, J. Colloid Interface Sci., 2011, 353, 549 CrossRef CAS PubMed; (l) K. Sumida, C. M. Brown, Z. R. Herm, S. Chavan, S. Bordiga and J. R. Long, Chem. Commun., 2011, 47, 1157 RSC; (m) W. L. Queen, C. M. Brown, D. K. Britt, M. R. Hudson and O. M. Yaghi, J. Phys. Chem. C, 2011, 115, 24915 CrossRef CAS; (n) Z. R. Herm, J. A. Swisher, B. Smit, R. Krishna and J. R. Long, J. Am. Chem. Soc., 2011, 133, 5664 CrossRef CAS PubMed; (o) J. A. Mason, K. Sumida, Z. R. Herm, R. Krishna and J. R. Long, Energy Environ. Sci., 2011, 4, 3030 RSC; (p) W. L. Queen, E. D. Bloch, C. M. Brown, M. R. Hudson, J. A. Mason, L. J. Murray, A. J. Ramirez-Cuesta, V. K. Peterson and J. R. Long, Dalton Trans., 2012, 41, 4180 RSC; (q) E. D. Bloch, W. L. Queen, R. Krishna, J. M. Zadrozny, C. M. Brown and J. R. Long, Science, 2012, 335, 1606 CrossRef CAS PubMed; (r) S. J. Geier, J. A. Mason, E. D. Bloch, W. L. Queen, M. R. Hudson, C. M. Brown and J. R. Long, Chem. Sci., 2013, 4, 2054 RSC.
- H. Wu, W. Zhou and T. Yildirim, J. Am. Chem. Soc., 2009, 131, 4995 CrossRef CAS PubMed.
- (a) S. S. Y. Chui, S. M. F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148 CrossRef CAS PubMed; (b) I. Senkovska and S. Kaskel, Microporous Mesoporous Mater., 2008, 112, 108 CrossRef CAS; (c) S. Cavenati, C. A. Grande, A. E. Rodrigues, C. Kiener and U. Müller, Ind. Eng. Chem. Res., 2008, 47, 6333 CrossRef CAS; (d) J. Moellmer, A. Moeller, F. Dreisbach, R. Glaeser and R. Staudt, Microporous Mesoporous Mater., 2011, 138, 140 CrossRef CAS; (e) P. Chowdhury, S. Mekala, F. Dreisbach and S. Gumma, Microporous Mesoporous Mater., 2012, 152, 246 CrossRef CAS; (f) N. C. Jeong, B. Samanta, C. Y. Lee, O. K. Farha and J. T. Hupp, J. Am. Chem. Soc., 2012, 134, 51 CrossRef CAS PubMed; (g) A. D. Wiersum, J.-S. Chang, C. Serre and P. L. Llewellyn, Langmuir, 2013, 29, 3301 CrossRef CAS PubMed.
- (a) E. García-Pérez, J. Gascón, V. Morales-Flórez, J. M. Castillo, F. Kapteijn and S. Calero, Langmuir, 2009, 25, 1725 CrossRef PubMed; (b) J. Getzschmann, I. Senkovska, D. Wallacher, M. Tovar, D. Fairen-Jimenez, T. Düren, J. M. van Baten, R. Krishna and S. Kaskel, Microporous Mesoporous Mater., 2010, 136, 50 CrossRef CAS; (c) H. Wu, J. M. Simmons, Y. Liu, C. M. Brown, X.-S. Wang, S. Ma, V. K. Peterson, P. D. Southon, C. J. Kepert, H.-C. Zhou, T. Yildirim and W. Zhou, Chem.–Eur. J., 2010, 16, 5205 CrossRef CAS PubMed.
- (a) S. Ma, D. Sun, J. M. Simmons, C. D. Collier, D. Yuan and H.-C. Zhou, J. Am. Chem. Soc., 2008, 130, 1012 CrossRef CAS PubMed; (b) S. M. P. Lucean, P. G. M. Mileo, P. F. G. Silvino and C. L. Cavalcante, Jr, J. Am. Chem. Soc., 2011, 133, 19282 CrossRef PubMed.
- (a) J. L. C. Roswell, A. R. Millward, K. S. Park and O. M. Yaghi, J. Am. Chem. Soc., 2004, 126, 5666 CrossRef PubMed; (b) A. G. Wong-Foy, A. J. Matzger and O. M. Yaghi, J. Am. Chem. Soc., 2006, 128, 3494 CrossRef CAS PubMed; (c) S. S. Kaye, A. Dailly, O. M. Yaghi and J. R. Long, J. Am. Chem. Soc., 2007, 129, 14176 CrossRef CAS PubMed; (d) H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. Ö. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 239, 424 CrossRef PubMed.
- (a) D. F. Quinn and J. A. MacDonald, Carbon, 1992, 30, 1097 CrossRef CAS; (b) J. A. F. MacDonald and D. F. Quinn, Fuel, 1998, 77, 61 CrossRef CAS; (c) L. Zhou, Y. Zhou, M. Li, P. Chen and Y. Wang, Langmuir, 2000, 16, 5955 CrossRef CAS.
- U. Stoeck, S. Krause, V. Bon, I. Senkovska and S. Kaskel, Chem. Commun., 2012, 48, 10841 RSC.
- Y. Peng, G. Srinivas, C. E. Wilmer, C. E. Wilmer, I. Eryazici, R. Q. Snurr, J. T. Hupp, T. Yildirim and O. K. Farha, Chem. Commun., 2013, 49, 2992 RSC.
- B. Li, Z. Zhang, Y. Li, K. Yao, Y. Zhu, Z. Deng, F. Yang, X. Zhou, G. Li, H. Wu, N. Nijem, Y. J. Chabal, Z. Lai, Y. Han, Z. Shi, S. Feng and J. Li, Angew. Chem., Int. Ed., 2012, 51, 1412 CrossRef CAS PubMed.
- Y. Wu, A. Kobayashi, G. J. Halder, V. K. Peterson, K. W. Chapman, N. Lock, P. D. Southon and C. J. Kepert, Angew. Chem., Int. Ed., 2008, 47, 8929 CrossRef CAS PubMed.
- S. Sircar, Ind. Eng. Chem. Res., 1992, 31, 1813 CrossRef CAS.
- See for example: ref 82, 87, 95, 104 and 116.
- L. Czepirski and J. Jagiełło, Chem. Eng. Sci., 1989, 44, 797 CrossRef CAS.
- K. A. G. Amankwah and J. A. Schwarz, Carbon, 1995, 33, 1313 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361 CrossRef CAS.
- See for example: (a) C. R. Clarkson, R. M. Bustin and J. H. Levy, Carbon, 1997, 35, 1689 CrossRef CAS; (b) J. H. Levy, S. J. Day and J. S. Killingley, Fuel, 1997, 76, 813 CrossRef CAS; (c) M.-A. Richard, P. Bénard and R. Chahine, Adsorption, 2009, 15, 43 CrossRef CAS.
- R. Krishna and J. R. Long, J. Phys. Chem. C, 2011, 115, 12941 CAS.
- See for example: ref 45a, 46c, 83, 87 and 92.
- K. Sillar and J. Sauer, J. Am. Chem. Soc., 2012, 134, 18354 CrossRef CAS PubMed.
- Y. He, W. Zhou, T. Yildirim and B. Chen, Energy Environ. Sci., 2013, 6, 2735 CAS.
- R. Saidur, M. Rezaei, W. K. Muzammil, M. H. Hassan, S. Paria and M. Hasanuzzaman, Renewable Sustainable Energy Rev., 2012, 16, 5649 CrossRef CAS.
- Y. Peng, V. Krungleviciute, I. Eryazici, J. T. Hupp, O. K. Farha and T. Yildirim, J. Am. Chem. Soc., 2013, 135, 11887 CrossRef CAS PubMed.
- B. Yilmaz, N. Trukhan and U. Müller, Chin. J. Catal., 2012, 33, 3 CrossRef CAS.
- S. K. Bhatia and A. L. Myers, Langmuir, 2006, 22, 1688 CrossRef CAS PubMed.
- E. Garrone, B. Bonelli and C. Otero Areán, Chem. Phys. Lett., 2008, 456, 68 CrossRef CAS.
- NIST Handbook 44 – 2012 Edition, “Specifications, Tolerances, and Other Technical Requirements for Weighing and Measuring Devices”, 2012, D-13.
- U.S. Dept. of Energy, 2013, http://www.fueleconomy.gov/feg/drivehabits.shtml.
- K. J. Chang and O. Talu, Appl. Therm. Eng., 1996, 16, 359 CrossRef CAS.
- L. L. Vasiliev, L. E. Kanonchik, D. A. Mishkinis and M. I. Rabetsky, Int. J. Therm. Sci., 2000, 39, 1047 CrossRef CAS.
- B. Mu and K. S. Walton, J. Phys. Chem. C, 2011, 115, 22748 CAS.
- (a) B. L. Huang, Z. Ni, A. Millward, A. J. H. McGaughey, C. Uher, M. Kaviany and O. M. Yaghi, Int. J. Heat Mass Transfer, 2007, 50, 405 CrossRef CAS; (b) D. Liu, J. J. Purewal, J. Yang, A. Sudik, S. Maurer, U. Müller, J. Ni and D. J. Siegel, Int. J. Hydrogen Energy, 2012, 37, 6109 CrossRef CAS.
- (a) J. Aclañiz-Monge, C. Trautwein, M. Pérez-Cadenas and M. C. Román-Martínez, Microporous Mesoporous Mater., 2006, 126, 291 CrossRef; (b) R. Zacharia, D. Cossement, L. Lafi and R. Chahine, J. Mater. Chem., 2010, 20, 2145 RSC; (c) M. Tagliabue, C. Rizzo, R. Milllini, P. D. C. Dietzel, R. Blom and S. Zanardi, J. Porous Mater., 2011, 18, 289 CrossRef CAS; (d) J. J. Purewal, D. Liu, J. Yang, A. Sudik, D. J. Siegel, S. Maurer and U. Müller, Int. J. Hydrogen Energy, 2012, 37, 2723 CrossRef CAS; (e) G. W. Peterson, J. B. DeCoste, T. G. Glover, Y. Huang, H. Jasuja and K. S. Walton, Microporous Mesoporous Mater., 2013, 179, 48 CrossRef CAS.
- J. C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059 RSC.
- (a) W. Zhou and T. Yildirim, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 180301 CrossRef; (b) H. Wu, T. Yildirim and W. Zhou, Phys. Chem. Lett., 2013, 4, 925 CrossRef CAS PubMed.
- (a) M. Greenbank, U.S. Pat., 4,972,658, 1990; (b) C. H. Chang, U.S. Pat., 5,308,821, 1994.
- L. Arnold, G. Averlant, S. Marx, M. Weickert, U. Müller, J. Mertel, C. Horch, M. Peksa and F. Stallmach, Chem. Ing. Tech., 2013, 85, 1 CrossRef.
- (a) J. P. B. Mota, AIChE J., 1999, 45, 986 CrossRef CAS; (b) O. Pupier, V. Goetz and R. Fiscal, Chem. Eng. Process., 2005, 44, 71 CrossRef CAS.
- http://www.uniongas.com/about-us.about-natural-gas/Chemical-Composition-of-Natural-Gas .
- Z. Lu, L. Du, K. Tang and J. Bai, Cryst. Growth Des., 2013, 13, 2252 CAS.
- J. Y. Lee, L. Pan, X. Huang, T. J. Emge and J. Li, Adv. Funct. Mater., 2011, 21, 993 CrossRef CAS.
- Z. Guo, H. Wu, G. Srinivas, Y. Zhou, S. Xiang, Z. Chen, Y. Yang, W. Zhou, M. O'Keeffe and B. Chen, Angew. Chem., Int. Ed., 2011, 50, 3178 CrossRef CAS PubMed.
- X.-S. Wang, S. Ma, K. Rauch, J. M. Simmons, D. Yuan, X. Wang, T. Yildirim, W. C. Cole, J. J. López, A. de Meijere and H.-C. Zhou, Chem. Mater., 2008, 20, 3145 CrossRef CAS.
- D. Liu, H. Wu, S. Wang, Z. Xie, J. Li and W. Lin, Chem. Sci., 2012, 3, 3032 RSC.
- D. Sun, S. Ma, J. M. Simmons, J.-R. Li, D. Yuan and H.-C. Zhou, Chem. Commun., 2010, 46, 1329 RSC.
- X. Lin, I. Telepeni, A. J. Blake, A. Dailly, C. M. Brown, J. M. Simmons, M. Zoppi, G. S. Walker, K. M. Thomas, T. J. Mays, P. Hubberstey, N. R. Champness and M. Schröder, J. Am. Chem. Soc., 2009, 131, 2159 CrossRef CAS PubMed.
- X. Rao, J. Cai, J. Yu, Y. He, C. Wu, W. Zhou, T. Yildirim, B. Chen and G. Qian, Chem. Commun., 2013, 49, 6719 RSC.
- P. Rallapalli, D. Patil, K. P. Prasanth, R. S. Somani, R. V. Jasra and H. C. Bajaj, J. Porous Mater., 2010, 17, 523 CrossRef CAS.
- S. Bourrelly, P. L. Llewellyn, C. Serre, F. Millange, T. Loiseau and G. Férey, J. Am. Chem. Soc., 2005, 127, 13519 CrossRef CAS PubMed.
- T. Loiseau, C. Serre, C. Huguenard, G. Fink, F. Taulelle, M. Henry, T. Bataille and G. Férey, Chem.–Eur. J., 2004, 10, 1373 CrossRef CAS PubMed.
- A. Lyubchyk, I. A. A. C. Esteves, F. J. A. L. Cruz and J. P. B. Mota, J. Phys. Chem. C, 2011, 115, 20628 CAS.
- X. Duan, J. Yu, J. Cai, Y. He, C. Wu, W. Zhou, T. Yildirim, Z. Zhang, S. Xiang, M. O'Leeffe, B. Chen and G. Qian, Chem. Commun., 2013, 49, 2043 RSC.
- C. E. Wilmer, O. K. Farha, T. Yildirim, I. Eryazici, V. Krungleviciute, A. A. Sarjeant, R. Q. Snurr and J. T. Hupp, Energy Envrion. Sci., 2013, 6, 1158 RSC.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O'Keeffe and O. M. Yaghi, Science, 2002, 296, 469 CrossRef PubMed.
- H. Kim, D. G. Samsonenko, S. Das, G.-H. Kim, H.-S. Lee, D. N. Dybtsev, E. A. Berdonosova and K. Kim, Chem.–Asian J., 2009, 4, 886 CrossRef CAS PubMed.
- X. L. Zhao, D. Sun, S. Yuan, S. Feng, R. Cao, D. Yuan, S. Wang, J. Dou and D. Sun, Inorg. Chem., 2012, 51, 10350 CrossRef CAS PubMed.
- D. Yuan, D. Zhao, D. Sun and H.-C. Zhou, Angew. Chem., Int. Ed., 2010, 49, 5357 CrossRef CAS PubMed.
- D. Zhao, D. Yuan, A. Yakovenko and H.-C. Zhou, Chem. Commun., 2010, 46, 4196 RSC.
- H. Wang, J. Getzschmann, I. Senkovska and S. Kaskel, Microporous Mesoporous Mater., 2008, 116, 653 CrossRef CAS.
- Y. He, Z. Zhang, S. Xiang, H. Wu, F. R. Fronczek, W. Zhou, R. Krishna, M. O'Keeffe and B. Chen, Chem.–Eur. J., 2012, 18, 1901 CrossRef CAS PubMed.
- Y. He, S. Xiang, Z. Zhang, S. Xiong, C. Wu, W. Zhou, T. Yildirim, R. Krishna and B. Chen, J. Mater. Chem. A, 2013, 1, 2543 CAS.
- N. Klein, H. C. Hoffmann, A. Cadiau, J. Getzschmann, M. R. Lohe, S. Paasch, T. Heydenreich, K. Adil, I. Senkovska, E. Brunner and S. Kaskel, J. Mater. Chem., 2012, 22, 10303 RSC.
- W. Lu, D. Yuan, T. A. Makal, J.-R. Li and H.-C. Zhou, Angew. Chem., Int. Ed., 2012, 51, 1580 CrossRef CAS PubMed.
- H. J. Park, D.-W. Lim, W. S. Yang, T.-R. Oh and M. P. Suh, Chem.–Eur. J., 2011, 17, 7251 CrossRef CAS PubMed.
- X. L. Zhao, D. Sun, S. Yuan, S. Feng, R. Cao, D. Yuan, S. Wang, J. Dou and D. Sun, Inorg. Chem., 2012, 51, 10350 CrossRef CAS PubMed.
- J. L. C. Rowsell and O. M. Yaghi, J. Am. Chem. Soc., 2006, 128, 1304 CrossRef CAS PubMed.
- Y. He, H. Furukawa, C. Wu, M. O'Keeffe, R. Krishna and B. Chen, Chem. Commun., 2013, 49, 6773 RSC.
- D. Yuan, D. Zhao, D. Sun and H.-C. Zhou, Angew. Chem., Int. Ed., 2010, 49, 5357 CrossRef CAS PubMed.
- N. Klein, I. Senkovska, I. A. Baburin, R. Grünker, U. Stoeck, M. Schlichtenmayer, B. Streppel, U. Mueller, S. Leoni, M. Hirscher and S. Kaskel, Chem.–Eur. J., 2011, 17, 13007 CrossRef CAS PubMed.
- J. Pérez-Pellitero, H. Amrouche, F. R. Siperstein, G. Pirngruber, C. Nieto-Draghi, G. Chaplais, A. Simon-Masseron, D. Bazer-Bachi, D. Peralta and N. Bats, Chem.–Eur. J., 2010, 16, 1560 CrossRef PubMed.
- T. K. Prasad and M. P. Suh, Chem.–Eur. J., 2012, 18, 8673 CrossRef CAS PubMed.
- J. L. Mendoza-Cortés, S. S. Han, H. Furukawa, O. M. Yaghi and W. A. Goddard III, J. Phys. Chem. A, 2010, 114, 10824 CrossRef PubMed.
- S. Noro, R. Kitaura, M. Kondo, S. Kitagawa, T. Ishii, H. Matsuzaka and M. Yamashita, J. Am. Chem. Soc., 2002, 124, 2568 CrossRef CAS PubMed.
- S. Noro, S. Kitagawa, M. Kondo and K. Seki, Angew. Chem., Int. Ed., 2000, 39, 2082 CrossRef CAS.
- M. Park, D. Moon, J. W. Yoon, J.-S. Chang and M. S. Lah, Chem. Commun., 2009, 2026 RSC.
- T. K. Prasad, D. H. Hong and M. P. Suh, Chem.–Eur. J., 2010, 16, 14043 CrossRef CAS PubMed.
- I. Senkovska, F. Hoffmann, M. Fröba, J. Getzschmann, W. Böhlmann and S. Kaskel, Microporous Mesoporous Mater., 2009, 122, 93 CrossRef CAS.
- M. C. Das, H. Xu, Z. Wang, G. Srinivas, W. Zhou, Y.-F. Yue, V. N. Nesterov, G. Qian and B. Chen, Chem. Commun., 2011, 47, 11715 RSC.
- P. L. Llewellyn, S. Bourrelly, C. Serre, A. Vimont, M. Daturi, L. Hamon, G. D. Weireld, J.-S. Chang, D.-Y. Hong, Y. K. Hwang, S. H. Jhung and G. Férey, Langmuir, 2008, 24, 7245 CrossRef CAS PubMed.
- J. I. Feldblyum, D. Dutta, A. G. Wong-Foy, A. Dailly, J. Imirzian, D. W. Gidley and A. J. Matzger, Langmuir, 2013, 29, 8146 CrossRef CAS PubMed.
- N. Klein, I. Senkovska, K. Gedrich, U. Stoeck, A. Henschel, U. Mueller and S. Kaskel, Angew. Chem., Int. Ed., 2009, 48, 9954 CrossRef CAS PubMed.
- T. K. Prasad and M. P. Suh, Chem.–Eur. J., 2012, 18, 8673 CrossRef CAS PubMed.
- D. Han, F.-L. Jian, M.-Y. Wu, L. Chen, Q.-H. Chen and M.-C. Hong, Chem. Commun., 2011, 47, 9861 RSC.
- J. Pérez-Pellitero, H. Amrouche, F. R. Siperstein, G. Pirngruber, C. Nieto-Draghi, G. Chaplais, A. Simon-Masseron, D. Bazer-Bachi, D. Peralta and N. Bats, Chem.–Eur. J., 2010, 16, 1560 CrossRef PubMed.
- Y. Yan, S. Yang, A. J. Blake, W. Lewis, E. Poirier, S. A. Barnett, N. R. Champness and M. Schröder, Chem. Commun., 2011, 47, 9995 RSC.
- M. K. Sharma, I. Senkovska, S. Kaskel and P. K. Bharadwaj, Inorg. Chem., 2011, 50, 539 CrossRef CAS PubMed.
- K. Gedrich, I. Senkovska, N. Klein, U. Stoeck, A. Henschel, M. R. Lohe, I. A. Baburin, U. Mueller and S. Kaskel, Angew. Chem., Int. Ed., 2010, 49, 8489 CrossRef CAS PubMed.
- R. Grünker, I. Senkovska, R. Biedermann, N. Klein, M. R. Lohe, P. Müller and S. Kaskel, Chem. Commun., 2011, 47, 490 RSC.
- M. Konda, M. Shimamure, S. Noro, S. Minakoshi, A. Asami, K. Seki and S. Kitagawa, Chem. Mater., 2000, 12, 1288 CrossRef.
- H. J. Park, Y. E. Cheon and M. P. Suh, Chem.–Eur. J., 2010, 16, 11662 CrossRef CAS PubMed.
- (a) K. Seki, Chem. Commun., 2001, 1496 RSC; (b) K. Seki and W. Mori, J. Phys. Chem. B, 2002, 106, 1380 CrossRef CAS.
- P. L. Llewellyn, S. Bourrelly, C. Vagner, N. Heymans, H. Leclerc, A. Ghoufi, P. Bazin, A. Vimont, M. Daturi, T. Devic, C. Serre, G. D. Weireld and G. Maurin, J. Phys. Chem. C, 2013, 117, 962 CAS.
- R. Kitaura, K. Seki, G. Akiyama and S. Kitagawa, Angew. Chem., Int. Ed., 2003, 42, 428 CrossRef CAS PubMed.
- H. Furukawa and O. M. Yaghi, J. Am. Chem. Soc., 2009, 131, 8875 CrossRef CAS PubMed.
- D. Yuan, W. Lu, D. Zhao and H.-C. Zhou, Adv. Funct. Mater., 2011, 23, 3723 CrossRef CAS PubMed.
- (a) P. D. Rolniak and R. Kobayashi, AIChE J., 1980, 26, 616 CrossRef CAS; (b) Q. H. Dirar and K. F. Loughlin, Adsorption, 2013 DOI:10.1007/s10450-013-9543-2.
Footnote |
| † Electronic supplementary information (ESI) available: Details of metal–organic framework synthesis and characterization, powder X-ray diffraction patterns, 77 K N2 adsorption isotherms, density calculations, high-pressure adsorption experimental details, background high-pressure CH4 adsorption isotherms, excess and total CH4 adsorption isotherms, description of isotherm fitting, table of fitted parameters, description of isosteric heat of adsorption calculations, correlations between surface area and uptake, usable capacity plots for different adsorption/desorption conditions, description of optimal binding enthalpy calculations, raw experimental data, and an electronic version of Table 2. See DOI: 10.1039/c3sc52633j |
| This journal is © The Royal Society of Chemistry 2014 |