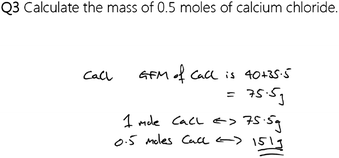View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C4RP00078A (Paper) Chem. Educ. Res. Pract., 2014, 15, 568-575

A simulated peer-assessment approach to improving student performance in chemical calculations†

Fraser J. Scott
Gryffe High School, Old Bridge of Weir Road, Houston, Renfrewshire, PA6 7EB, UK. E-mail: fraser.j.scott@strath.ac.uk

Received 7th April 2014 , Accepted 26th April 2014

First published on 28th April 2014

Abstract

This paper describes the utility of using simulated, rather than real, student solutions to problems within a peer-assessment setting and whether this approach can be used as a means of improving performance in chemical calculations. The study involved a small cohort of students, of two levels, who carried out a simulated peer-assessment as a classroom activity and their improvement in performance and attitude towards the activity was measured. The results demonstrate that a simulated peer-assessment approach can be successfully used in lieu of standard peer-assessment and that student attitudes favour the simulated approach.

Introduction

Mathematical deficiencies review

Mathematical proficiency is fundamental to be able to understand and describe a plethora of scientific phenomena. The lack of it in high school education, and its impact on science, has been the focus of much media attention of late (Royal Society of Chemistry, 2009a, 2012a, 2012b); furthermore, a recent report from SCORE (Science Community Representing Education), a collaboration of leading science organisations, has revealed that a significant proportion of the mathematical requirements of high school science courses are not assessed, propagating the problem (Science Community Representing Education, 2010). The importance of this has led to the development of several initiatives by the Royal Society of Chemistry to address this concern (Royal Society of Chemistry, 2009b, 2009c).

Student mathematical proficiency is frequently commented on within the field of chemistry education due to the direct impact it has on the global curricular theme of “chemical calculations”. It has been noted by Obande (2003) that issues that students have in mathematics are transferred to the chemistry classroom and with this, difficulties in chemical calculations ensue. Furthermore, research on the difference in performance between the genders in the area of chemical calculations has been attributed to differing mathematical ability. Williams and Jacobson (1990) demonstrate that there are no differences in the achievement of boys and girls in the early years of education; however, in the later stages, boys outperform girls in calculation based curricular areas because of better mathematical understanding. A study by Lazonby et al. (1982) into the impact of problem solving skills in chemistry calculations indicates that students' inability to perform a series of basic mathematical operations is significantly damaging to their overall performance. Leopold and Edgar (2008) have similarly demonstrated the relationship between mathematical ability and success at undergraduate level chemistry. They note that the basic mathematical ability of non-calculator skills is particularly important. These research findings begin to highlight the criticality of basic mathematical proficiency.

There is an opposing camp of thought who argue that the major contributory factor is not student mathematical ability. When examining stoichiometric calculations, Gabel and Sherwood (1984) commented that underachievement was linked to poor understanding of the basic concepts of the topic. They identified that the use of the word “mole” was a confusing factor for students due to a lack of understanding of its meaning. A linguistic argument was put forward by Novick and Menis (1976) in that they identified the phonetic similarity between the word “mole” and “molecule” or “molecular” to be a significant source of confusion. The lack of understanding of the mole concept is not just restricted to students; it has been suggested by Strömdahl et al. (1994) that through IUPAC's (International Union of Pure and Applied Chemistry) numerous alterations to the definition of the mole, even scientists and educators possess misconceptions.

Peer-assessment review

Peer-assessment is defined as the process of evaluating the quality or success of the outcomes of a peer or peers (Topping, 1998) and is followed by the provision of feedback (Van Den Berg et al., 2006). Whilst feedback is of great benefit to a student who wishes to improve, the evaluation process that a student must participate in to provide feedback is arguably the most important aspect of peer assessment. In evaluating a peer's work, a student is exercising the skills required to examine their own work; peer assessment and self-assessment are thus intrinsically linked.

There are many proponents of the importance of peer and self-assessment. Boud (1995) and McDonald and Boud (2003, p. 210) have argued that the development of these skills is of great importance, not just at isolated levels of a curriculum, but throughout all stages of education. Moreover, after a thorough review of the literature, Black and William (1998) posit that self-assessment is “not an interesting option or luxury: it has to be seen as essential” (pp. 54–55). These opinions are held up in practice: Rust et al. (2003) and O'Donovan et al. (2004) have shown that students who had participated in a peer-assessment programme at the beginning of a course of study demonstrated an enhancement in performance over those who did not participate.

O'Donovan et al. (2004) report that by involving students in the marking process, they can expand the assessment of learning into an effective learning tool and generate a technique of assessment for learning. Peer and self-assessment techniques thus enable a student to become more autonomous in their learning and help to develop a student's ability to identify their own learning needs (Brown and Knight, 1994; Elwood and Klenowski, 2002). The skills gained through peer and self-assessment are therefore crucial to the developing student as only through identifying their own learning needs can they efficiently improve and engage fully with education. Without such skills, a student's attainment, in education and beyond, will suffer. Harlen (2007) describes the necessity of a student becoming responsible for their own learning due to the benefit it brings on their life after school and, more broadly, society as a whole. Candy et al. (1994) attest to the importance of peer and self-assessment in stating that diagnosis of educational needs is fundamental to successful lifelong learning.

The benefits of peer-assessment techniques are also appreciated by the students receiving their education through such techniques. Bryant and Carless (2009) investigated the views of primary school students to peer-assessment and found that the facility to learn from each other whilst taking responsibility for their own work resulted in a very positive reception. The students from this study were particularly aware of the advantages peer-assessment brought in identifying errors they were likely to make which could then be avoided in future exams. In a study into perceptions of secondary school students, Peterson and Irving (2008) discovered that students believed that the feedback provided through peer-assessment was a motivational tool that encouraged them to seek out new information to correct their errors. High school students are even aware of the broader benefits; White (2009) reports that students found peer-assessment a positive experience due to the opportunity to enhance skills which they believed were helpful for their future career. Perhaps most importantly, students find peer-assessment fun (Peterson and Irving, 2008).

The advantages that peer assessment brings to students are both numerous and significant; however, it has been argued that there are some potential issues that need consideration before implementation. A study by Wen and Tsai (2006) looked into university students' attitudes towards peer assessment. This investigation revealed that students had a generally positive attitude towards peer assessment; however, there was a lack of self-confidence with respect to marking their classmates' work and, reciprocally, they were apprehensive about being criticised by their peers. These findings are supported in a study by Karaca (2009) into teacher trainees' opinions of peer assessment in which it was suggested that students might not be capable of evaluating their peers effectively, leading to the generation of deleterious feedback. This study also indicated that students' evaluations could be influenced by their social relationships with others in the class; friendly students would be prone to being too generous with positive feedback whilst rivalries enhanced the provision of negative feedback. A study by Ballantyne et al. (2002) has also reported that students can be apprehensive about peer-assessment due to it being excessively time-consuming.

Bostock (2000) and White (2009) have further investigated the potential problems in peer assessment. They assert that validity and reliability of assessment by students may be an issue as the feedback provided may not be accurate or valuable and even that students may not take the assessment process seriously. Moreover, they agree with Karaca (2009) that students may not be qualified enough to be able to evaluate each other and that students may be influenced by friendships and solidarity among themselves. Bostock (2000) and White (2009) also note that the lack of teacher input to the evaluation process may lead to students providing mis-information.

It has been found by Bryant and Carless (2009) that a student's perception of peer assessment can differ depending on their language proficiency and that of their peer. Those students who were assessed by peers with greater language proficiency commented that it was difficult to assess their peer's work due to the ability difference; contrariwise, more able students found that their peers could not provide useful feedback. Teachers were identified as a more reliable source of feedback.

The purpose of this study

This study aimed to investigate a method of utilising a peer-assessment method to improve high school student performance in chemistry calculations. The chemistry calculations that have been chosen are those expected from candidates sitting Chemistry courses at the National 5 and Higher levels of the Scottish education system. It is the author's view that one of the main factors affecting performance in these calculations is the poor mathematical ability of students (Scott, 2012); however, methods are sought to ameliorate this problem that can be utilised in a chemistry classroom. Completion of a calculation based peer-assessment activity was thought to be an appropriate method to improve student performance. In an effort to reduce the negative aspects of peer-assessment, this study explores the use of a simulated peer-assessment design. In this guise, the students are provided with an example of an incorrect solution to a question and their goal is to analyse and provide feedback. Through removing the students' own work from the assessment proceedings, the negative aspects such as apprehension about being criticised; provision of deleterious feedback; influence of social relationships; and, differing peer abilities should be removed. The simulated design is not thought to detract from the positive aspects of peer-assessment as it still allows for the students to participate in the evaluation process.

Research questions

The purpose of this study was to utilise a mixed-methods research design to examine the usefulness of a simulated peer-assessment activity in improving student ability in high school chemical calculations. Three research questions were identified:

(1) Does participation in the simulated peer-assessment activity increase student performance in basic chemical calculations?

(2) Would students' attitudes to the activity be different if the activity was not simulated but instead a straightforward peer-assessment?

Research methodology

Activity design

Two activities, similar in design, were developed. One for use with students sitting the National 5 Chemistry course and one for those sitting the Higher Chemistry course. These activities provide students with a series of questions as would be expected of those sitting the appropriate course and, along with each question, a sample solution is also provided (Fig. 1). The solution, however, is incorrect and the aim of the activity is for students to identify any errors present, write a comment beside the solution to explain why there is an error (like a teacher might) and to provide a correct solution to the question.
image file: c4rp00078a-f1.tif
Fig. 1 Example of a simulated solution a student would analyse (error present).

The activity for the students sitting the National 5 Chemistry course contains questions of three types, arranged in increasing order of difficulty, and of each question type there are three examples, to give nine questions in total. The first type of question involves the calculation of the mass of a given number of moles of a substance. The second type of question requires the students to find the number of moles given the mass of a substance. The last type of question provides the students with a balanced reaction equation and requires the students to calculate the mass of one substance given the mass of another. These are commonly encountered calculations for students at this level (Fig. 2).


image file: c4rp00078a-f2.tif
Fig. 2 Examples of questions for the National 5 Chemistry activity (no solutions shown). First type of question, top, second type, middle, third type, bottom.

The activity for the students sitting the Higher Chemistry course also contains questions of three types and there are three of each to give a total of nine questions. The first type of question requires the students to calculate the mass of a substance given the concentration and volume of another and a balanced reaction equation. The second type of question involves the use of the molar volume of gases at STP and calculating the number of moles, or volume, of a gas. The last type of question involves the use of Avogadro's constant to calculate the number of ions or atoms present in a given mass of a substance. Again, these style of questions are commonly encountered by students at this level (Fig. 3).


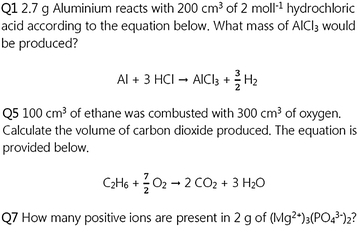image file: c4rp00078a-f3.tif
Fig. 3 Examples of questions for the Higher Chemistry activity (no solutions shown). First type of question, top, second type, middle, third type, bottom.

The simulated solutions to the questions provided to the students include a spread of common errors that students often make and are solved using a variety of common strategies, as identified through personal experience and through discourse with multiple, practising chemistry educators. The simulated peer-assessment activities for both levels can be found in Appendix 2 (ESI†).

The participants of these activities were arranged into pairs or groups of three and were given the question sheets to work through one at a time. Working in groups was an important aspect of these activities as it promoted discussion and idea sharing within the pair in order for them to discover the error and provide feedback. The discussion throughout the activity allowed the students to become more aware of the common errors they are likely to make in their own work and thus prevent them from making them in the future. As the students carried out the activity, the teacher roamed the classroom to answer any queries; however, minimal interaction with students was necessary as in most cases the groups were able to identify any errors present and provide a correct solution.

Study setting and participants

This study was carried out in a high school in Scotland during the run up to the national exams thus none of the content of each activity would be considered new to the participating students. Three National 5 Chemistry classes, of student age 15/16, and three Higher Chemistry classes, of student age 16/17, participated in the study. This gave a total of 47 students for the National 5 level activity and 54 for the Higher level. The classes were of mixed ability and sex and had different teachers within the same level of activity; the author was one of the teachers participating in administering the simulated peer-assessment activities.

Permission was obtained from the head teacher of the school before this research was carried out. Pupils were required to sign a research consent form to allow the data generated to be analysed; however, every pupil in the classes participated in the activity.

Data sources

A mixed-method research design was utilised during this study in order to extract a variety of information. The data sources included a pre-test, post-test and a student attitude questionnaire.
Pre and post tests. For each level of activity, two sets of three questions, which were analogous to the types found within the simulated peer-assessment activities, were developed to measure the prior knowledge (pre-test) and resultant knowledge (post-test) of the participants before and after the activities were carried out. These questions were designed to eliminate as many as possible purely chemical errors from students such as incorrect formulas or equations by providing such information in the question. The questions in the pre-test and the post-test were analogous and so formed three matched pairs which could be used to assess any increase in student ability due to the completion of the simulated peer-assessment activities. The full test scripts can be found in Appendix 1 (ESI†). In order to ensure content validity of both the pre and post-tests multiple, practising chemistry educators contributed to the final design.
Student attitude questionnaire. This is a self-reported questionnaire that consists of three Likert-scale items. Students were asked to respond using a scale of 1 to 5, where 1 = strongly disagree and 5 = strongly agree. The questions posed to the students were as follows:

(1) Did you enjoy this activity?

(2) Would you have preferred to have been marking one of your classmate's work, rather than some simulated work?

(3) Would you have been happy to have your work assessed by others in your class?

Research procedure

The pre-test was carried out by the students at the beginning of the lesson in which they completed the simulated peer-assessment activity. There was not a time limit put on the students as they completed this but it was completed by all within approximately 15 minutes. Students were not made aware of their performance on this test until after the entire research activity had been completed. The students then participated in the simulated peer-assessment activity for the remainder of the lesson which lasted another 35 minutes, approximately (lessons are 50 minutes each). The students were informed that they did not need to complete all of the example questions and were encouraged to work at their own pace; however they were guided to ensure they had attempted all the different types of questions. Very few students did not complete all the questions in the activity. During the next lesson the students carried out the student attitude questionnaire and this was followed by the post-test which again was not subjected to a time limit but was completed in approximately 15 minutes.

Data analysis

Students' responses to the pre and post-tests were scored in a binary fashion as either correct or incorrect. This generated a correct answer rate for each student on each test and a paired t-test was run to examine any overall difference in performance. The pre and post-test combination also made a series of three matched pairs; as such, a McNemar test was employed. The student's mathematical ability was estimated from their working grade in Mathematics, which was made available by the mathematics department within the school. This was used as a factor in an ANOVA calculation to determine its influence on student performance. Students' responses to the questionnaire were analysed by plotting histograms.

Results and discussion

Pre-test and post-test

First the data for the National 5 Chemistry course are analysed below. The mean correct answer rate for student performance on the pre-test was 56.7% (SD = 31.0%, Table 1) which indicates a fairly wide range of performances on this test. The mean correct answer rate for student performance on the post-test was 79.4% (SD = 22.6%, Table 1) and the result of the paired t-test indicated that there was a significant improvement of 22.7% on the post-test compared to the pre-test at a 95% significance level (t = 5.96, P-value < 0.001, Table 1).
Table 1 Comparison of the mean correct answer rate between the pre-test and the post-test of National 5 students
N Pre-test (%) Post-test (%) t-value P-value
Mean SD Mean SD
47 56.7 31.0 79.4 22.6 5.96 <0.001

To provide further insight, the pre-test and post-test were subjected to a McNemar test to examine the increase in performance on individual questions (Table 2). It can be seen from Table 2 that there is strong evidence to indicate that there has been a significant improvement in performance in the first and third questions in the post-test compared to the pre-test (P-value = 0.004 and <0.001, respectively). Whereas, for question 2 there is slightly less strong evidence of improvement (P-value = 0.0.021). These data suggest that the increase in performance is across all the questions encountered in the pre and post-tests rather than just localised to improvement in a single question.

Table 2 McNemar analysis of pre-test and post-test of National 5 students
Question 1 2 3
P-value 0.004 0.021 <0.001

Each student's overall gain in performance between the pre and post-test was subjected to an ANOVA using their Mathematics working grade as the factor within the analysis. The working grades are scored as A through to D with A being the highest working grade. The results of this analysis are shown in Table 3.

Table 3 ANOVA results using mathematics working grade as a factor of National 5 students
Mathematics working grade N Mean gain (%) SD (%) F-value P-value
A 11 9.1 15.6 4.53 0.008
B 15 37.8 27.8
C 15 26.7 22.5
D 6 5.6 25.1

The P-value for this ANOVA shows a significant difference in the mean gain in performance between the different Mathematics working grades. Those students who were of intermediate mathematical ability, i.e. working grades B and C, demonstrated the greatest increase in performance after taking part in the simulated peer-assessment activity. For those of working grade B there was a 37.8% increase (SD = 27.8%) and those of working grade C showed a 26.7% increase (SD = 22.5%). Contrariwise, the students with a working grade A and those with a working grade of D demonstrated a much smaller increase in performance. Those students with a working grade of A had a mean gain of 9.1% (SD = 15.6%) and those of working grade D displayed a 5.6% increase in performance (SD = 25.1%).

The data for the Higher Chemistry course was subject to the same panel of statistical analyses. The mean correct answer rate for student performance on the pre-test was 46.9% (SD = 37.5%, Table 4) and the mean correct answer rate for student performance on the post-test was 68.5% (SD = 35.1%, Table 1). The result of the paired t-test indicated that there was a significant improvement of 21.6% on the post-test compared to the pre-test at a 95% significance level (t = 6.10, P-value < 0.001, Table 4).

Table 4 Comparison of the mean correct answer rate between the pre-test and the post-test of Higher students
N Pre-test (%) Post-test (%) t-value P-value
Mean SD Mean SD
54 46.9 37.5 68.5 35.1 6.10 <0.001

As before, the pre-test and post-test were subjected to a McNemar test to examine the increase in performance on individual questions (Table 5). It can be seen from Table 5 that there is strong evidence to indicate that there has been a significant improvement in performance in all of the questions individually in the post-test compared to the pre-test (P-value = 0.001, 0.002 and 0.008, respectively). This result is similar to that seen in the analysis of the National 5 Chemistry students; the increase in performance is across all the questions encountered in the pre and post-tests.

Table 5 McNemar analysis of pre-test and post-test of Higher students
Question 1 2 3
P-value 0.001 0.002 0.008

The ANOVA results on the gain in score from pre to post-test using Mathematics working grade of the Higher Chemistry students are shown in Table 6.

Table 6 ANOVA results using mathematics working grade as a factor of higher students
Mathematics working grade N Mean gain (%) SD (%) F-value P-value
A 15 2.2 8.6 20.97 <0.001
B 16 47.9 24.2
C 16 22.9 20.1
D 7 0.0 0.0

The P-value for this ANOVA again shows a significant difference in the mean gain in performance between the different Mathematics working grades. The students who were of intermediate mathematical ability, displayed the greatest increase in performance between pre and post-tests. Those of working grade B showed a 47.9% increase (SD = 24.2%) and those of working grade C showed a 22.9% increase (SD = 20.1%). This is in contrast to the other students: those with a working grade A had a mean gain of only 2.2% (SD = 8.6%) and those of working grade D displayed absolutely no increase.

The statistical analyses of the effects of the simulated peer-assessment activity at National 5 level and at Higher level demonstrate similar outcomes. At both levels there is a significant improvement in student ability to perform chemical calculation across the spectrum of type of question that were encountered in the pre and post-tests. Of particular interest are the results of the ANOVA calculations using Mathematics working grade as the factor for analysis. At both levels of activity there was a significant increase in mean gain of score for those students with a working grade of B or C; however, there was a much less significant or negligible increase in mean gain of score for those with a working grade of A or D. The small increase in performance of the working grade A group of students can be explained due to their score on the pre-test being particularly high. The average pre-test score for the National 5 students was 91.0% (SD = 15.6%) and that for the Higher students was 93.3% (SD = 13.8%) and thus there is little room for improvement on chemical calculation for these mathematically capable students. It is still thought that participation in this activity is useful for this set of students as their understanding of the chemistry involved is reinforced. Students who were of intermediate mathematical ability, as defined by a Mathematics working grade of B or C, exhibited the greatest improvement in performance between the pre and post-tests. Their possession of at least a basic grasp of mathematics allows this group of students to engage with the simulated peer-assessment activity, through discussion of the simple mathematical steps involved, and allows them to improve. For both the National 5 and the Higher set of students there is a greater mean gain in score for those of a higher mathematics working grade across grades B through D (see Tables 3 and 6). This correlation between mathematical ability and improvement in performance in chemical calculations, after participating in the activity, highlights the significance of mathematical proficiency to chemical calculations. It is thought that a lack of basic mathematical skill is the reason that those students of working grade D exhibit negligible increase performance between the pre and post-tests. If this set of students are not proficient with using basic mathematical skills such as the use of ratios, which are essential for answering most chemical calculations, then they will not be able to engage in discussion with others in order to locate and solve the errors presented to them in the simulated peer-assessment activity. This feature of the data suggests that there is a group of students who could benefit from explicit instruction in simple mathematical techniques before contextualising these within chemistry. This author has previously asserted that students struggle with applying simple mathematical skills in a chemistry setting due to being taught in an algorithmic fashion in mathematics classes (Scott, 2012).

Overall, the analysis of these data suggest that the simulated peer-assessment activity had a positive effect on student performance in basic chemical calculations.

Student attitude questionnaire

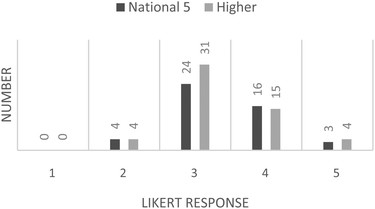
The responses from the Likert-scale items were collated and have been displayed as histograms. Students were asked to respond using a scale of 1 to 5, where 1 = strongly disagree and 5 = strongly agree. Responses to the question “Did you enjoy this activity?” are presented in Fig. 4. It can be seen that the responses for “did you enjoy this activity?” are slightly left-skewed and indicative of an overall enjoyable activity. This is rather pleasing as it is often difficult to find a worthwhile learning activity that students actually enjoy.
image file: c4rp00078a-f4.tif
Fig. 4 Student responses to question 1: “Did you enjoy this activity?”.

The student responses to “Would you have preferred to have been marking one of your classmates work, rather than some simulated work” are presented in Fig. 5. The responses for both the National 5 and Higher students are both right-skewed, the Higher slightly more so, which indicates an indifference to this statement leaning towards disagreement. The student responses to “Would you have been happy to have your work assessed by others in your class?” are presented in Fig. 6.


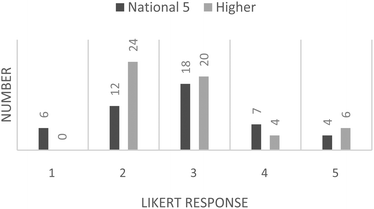image file: c4rp00078a-f5.tif
Fig. 5 Student responses to question 2: “Would you have preferred to have been marking one of your classmates work, rather than some simulated work”.

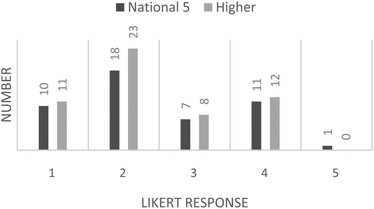image file: c4rp00078a-f6.tif
Fig. 6 Student responses to question 3: “Would you have been happy to have your work assessed by others in your class?”.

The final question on the student response questionnaire shows an overall right-skewed data response; however, the data are bimodal, with modes appearing at “disagree” and “agree” on the Likert-scale.

The students' responses to question 3 of the questionnaire indicate that the majority of the students would not be happy about their peers assessing their work. This is in alignment with the previously asserted disadvantages of peer-assessment. This serves to illustrate the usefulness of a “simulated” approach to peer-assessment and validates the activity used in this study. Furthermore, the students' responses to question 2 of the questionnaire indicate that the use of simulated material does not result in dissatisfaction for the students. It would be interesting to find out why the students would not have preferred to be marking a peer's work. Perhaps this is evidence of conscientious students not wanting to risk providing a peer with a quality of feedback that is not as good as that a teacher could provide; or, possibly, it demonstrates feelings of inadequacy with regards to their abilities. The bimodal distribution from the students' responses to question 3 of the questionnaire is an interesting feature of the data. It is worth noting that of the 24 students across both levels who responded positively, i.e. were happy to have their work assessed by another, 75% of them achieved full marks on their pre-test with the remaining 25% gaining two out of three questions correct. Thus this may be due to a sub-set of the students being particularly confident in their ability at performing calculations and hence they are happy for others to assess their work.

Conclusions

This study has demonstrated that a simulated peer-assessment approach can be utilised effectively to promote student performance in the area of chemistry calculations which is in alignment with the first research question of this study. After participating in the activity students were able to avoid common sources of error and hence improve their performance as measured by a coupled pre-test and post-test. The simulated peer-assessment activity has been found to provide the greatest boost to those of intermediate mathematical ability. Students of lower mathematical ability would benefit from direct instruction in simple mathematical skills to allow them to benefit from participation in this activity.

The second research question was to find out how students' attitudes would be if the activity was not simulated but instead a straightforward peer-assessment. This was included in order to investigate whether a simulated approach can the address concerns over the negative aspects of peer-assessment. This study has confirmed that the majority of students would be unhappy to have their peers assessing their work, perhaps due to the poorer quality of feedback that would likely be provided. Moreover, this study has demonstrated that the replacement of a peer's work with simulated work does not result in a negative attitude from the students undertaking the activity. Simulated peer-assessment therefore provides a mechanism through which the benefits associated with peer-assessment can be provided without having to deal with the negative aspects such as poor quality of feedback or inconsistent feedback due to social networks within a class.

The utility of a simulated approach to peer-assessment is not confined to chemistry calculations but could easily be adapted to other relevant areas of the chemistry curriculum or, indeed, other subjects entirely.

Acknowledgements

The Author would like to thank Maggie McAleavy and Carolyn Jamison for their assistance during this study.

Notes and references

  1. Ballantyne R., Hughes K. and Mylonas A., (2002), Developing procedures for implementing peer assessment in large classes using an action research process, Assess. Eval. High. Educ., 27(5), 427–441.
  2. Black P. and William D., (1998), Assessment and classroom learning, Assess. Educ., 5(1), 7–74.
  3. Bostock S. J., (2000), Student peer assessment, A workshop at Keele University.
  4. Boud D., (1995), Enhancing learning through self assessment, Kogan Page, London.
  5. Brown S. and Knight P., (1994), Assessing learners in higher education, Kogan Page, London.
  6. Bryant D. A. and Carless D. R., (2009), Peer assessment in a test-dominated setting: empowering, boring or facilitating examination preparation?, Educ. Res. Policy Prac., 9(1), 3–15.
  7. Candy P. C., Crebert G. and O'Leary J., (1994), Developing lifelong learners through undergraduate education, Canberra: Australian Government Publishing Service. National Board of Employment, Education and Training Commissioned Report No. 28.
  8. Elwood J. and Klenowski V., (2002), Creating communities of shared practice: the challenges of assessment use in learning and teaching, Assess. Eval. High. Educ., 27, 243–256.
  9. Gabel D. and Sherwood R., (1984), Analysing difficulties with mole concept tasks by using familiar analogue tasks, J. Res. Sci. Teach., 21(8), 843–851.
  10. Harlen W., (2007), Assessment of learning, Sage, London.
  11. Karaca E., (2009), An evaluation of teacher trainees' opinions of the peer assessment in terms of some variables, World Appl. Sci. J., 6(1), 123–128.
  12. Lazonby J., Morris J. E. and Waddington D. J., (1982), The muddlesome mole, Educ. Chem., 19, 109–111.
  13. Leopold D. G. and Edgar B., (2008), Degree of Mathematics Fluency and Success in Second-Semester Introductory Chemistry, J. Chem. Educ., 85, 724–731.
  14. McDonald B. and Boud D., (2003), The Impact of self-assessment on achievement: the effects of self-assessment training on performance in external examinations, Assess. Educ., 10(2), 209–220.
  15. Novick S. and Menis J., (1976), A study of student perceptions of the mole concept, J. Chem. Educ., 53, 720–722.
  16. Obande M., (2003), Sex differences in the study of stoichiometry among secondary school students in Makurdi, Local Government, An unpublished PGDE Project BSU Makurdi.
  17. O'Donovan B., Price M. and Rust C., (2004), Know what I mean? Enhancing student understanding of assessment standards and criteria, Teach. High. Educ., 9(3), 325–335.
  18. Peterson E. R. and Irving S. E., (2008), Secondary school students' conceptions of assessment and feedback, Learn. Instr., 18(3), 238–250.
  19. Royal Society of Chemistry, (2009a), www.rsc.org/images/ACMERSCResponse_tcm18-170564.pdf, accessed 10/11/11.
  20. Royal Society of Chemistry, (2009b), http://www.rsc.org/images/Bulletin10_tcm18-134605.pdf, accessed 10/11/11.
  21. Royal Society of Chemistry, (2009c), http://discovermaths.rsc.org, accessed 10/11/11.
  22. Royal Society of Chemistry, (2012a), Is Maths to Blame?, Educ. Chem., 49(5), 7.
  23. Royal Society of Chemistry, (2012b), Criticism of maths in chemistry grows, Educ. Chem., 49(4), 3.
  24. Rust C., Price, M. and O'Donovan, B., (2003), Improving students' learning by developing their understanding of assessment criteria and processes, Assess. Eval. High. Educ., 28(2), 147–164.
  25. Science Community Representing Education, (2010), http://www.nationalstemcentre.org.uk/res/documents/page/SCORE%20report.pdf.
  26. Scott F., (2012), Is mathematics to blame? An investigation into high school students' difficulty in performing calculations in chemistry, Chem. Educ. Res. Pract., 13, 330–336.
  27. Strömdahl H., Tullberg A. and Lybeck L., (1994), The qualitatively different conceptions of 1 mol, Int. J. Sci. Educ., 16, 17–26.
  28. Topping K., (1998), Peer assessment between students in colleges and universities, Review of Educational Research, 68(3), 249–276.
  29. van den Berg I., Admiraal W. and Pilot A., (2006), Peer assessment in university teaching: evaluating seven course designs, Assessment & Evaluation in Higher Education, 31(1), 19–36.
  30. Wen M. L. and Tsai C. C., (2006), University students' perceptions of and attitudes toward (online) peer assessment, High. Educ., 51(1), 27–44.
  31. Williams D. and Jacobson S., (1990), Growth in maths skills during the intermediate years: sex differences and school effects, Int. J. Educ. Res., 14, 157–174.
  32. White E., (2009), Student perspectives of peer assessment for learning in a public speaking course, Asian EFL J., 33(1), 1–36.

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4rp00078a
This journal is © The Royal Society of Chemistry 2014