Orbitals in chemical education. An analysis through their graphical representations

Abstract

Students' understanding of the orbital concept has been subject to considerable research and debate and often found at variance with a quantum mechanical ideal. Could it be the case that orbitals as actually used by practising chemists in teaching and research also differ from that ideal? Our experience shows that this might often be the case. Through a series of examples of pictorial representations of orbitals found in textbooks and other educational materials, as well as in research papers, we argue that this is a common situation, which deserves to be stated explicitly. We point out that, in particular, there is a way in which orbitals are frequently employed deeply rooted in chemical thinking and compatible with a classical (in the sense of pre-quantum) approach. Many chemists employ quantum-like terms, and rely on concepts that look quantum, such as ‘orbital’, but they actually play on the well-known ground of the classical structural ideas that can be traced back to the work of pioneers like Cannizaro, Kekulé, or van't Hoff. We maintain that given the fundamental role of these semi-classical ideas in chemistry, it is nothing but natural to treat them in an equivalent fashion in chemical education.

---

Introduction

Why study visual representations?

Orbitals, a special type of mathematical functions used in the quantum description of the state of an atom or a molecule, play an important role in chemistry, which is consistent with the widely held† view that quantum mechanics lies at the foundations of chemistry (see for example Dirac, 1929 or Weinberg, 2003; p. 212).

The role played by orbitals in the formalism of quantum chemistry is far from being obvious. Solving the Schrödinger equation is a rather complex mathematical enterprise for almost every system of interest in chemistry. There are hardly a dozen model systems for which analytical solutions of the Schrödinger equation exist, and only one of them − the hydrogen atom − is of any relevance in chemistry. To obtain a wave function for any other realistic chemical system approximations must be adopted.

When it comes to molecules, a first simplification consists of factorizing the global wave function in a nuclear and an electronic part:

Ψ = Ψ_elΨ_nuc

This factorization is usually known as Born–Oppenheimer approximation. It enormously simplifies the resolution (and the chemical interpretation) of the Schrödinger equation, but further approximations are still required. The most popular one is to expand the electronic Ψ_el on the basis of monoelectronic functions. For a system with N electrons, such an approximation can be expressed as

Ψ_el(r₁,r₂,…,r_N) = ϕ₁(r₁)ϕ₂(r₂)…ϕ_N(r_N)

These approximations are known for obvious reasons as independent electron models.‡ These functions ϕ_n(r_n) are called orbitals in the language of quantum chemistry. Further approximations are usually required, but the basic pattern is almost always the one we have already presented.

Thus, the suitable framework for properly understanding these orbitals is that of quantum mechanics. On the other hand, quantum theory is noted for its highly non-intuitive character, so it is not surprising that a number of studies have called into question the usage of quantum mechanical concepts in introductory chemistry courses (including Tsaparlis, 1997; Coll and Treagust, 2001; Taber, 2002, 2004; Taber and Coll, 2003; Papaphotis and Tsaparlis, 2008a,b; Stefani and Tsaparlis, 2009 or Tsaparlis and Papaphotis, 2009).

Tsaparlis and Papaphotis (2002) went even further asking whether “quantum-chemical concepts are suitable for secondary students”, a question for which Sánchez Gómez and Martín (2003; p. 141) found a majority of negative answers in a survey of the literature.§

The above-mentioned analyses find that students often use quantum concepts, in particular that of the orbital, in a classical way or, more generally, that “the learners' mental models [are] simple and realist in nature” (Coll and Taylor, 2002). By ‘realist’ these authors mean that, in particular, mathematical quantum orbitals are thought of as actually existing physical objects. Most students, according to this line of argument, would believe that, for example, an isolated carbon atom has four hybrid sp³ orbitals distributed in a tetrahedron-like way around its nucleus.¶

Some authors talk about alternative conceptions or misconceptions, in particular about orbitals, which must be dealt with (for instance, Papaphotis and Tsaparlis, Taber or Coll and Taylor). Others (notably Gillespie et al. 1996) argue for the inadequacy of orbitals in introductory chemistry like this: quantum mechanics is conceptually difficult, so most introductory level students will be unable to grasp it properly, therefore orbitals are not to be taught in introductory chemistry courses.

Those trains of thought do have a solid internal logic, but on the other hand, as we shall see later, chemists do employ routinely their own version of orbitals, termed chemical by Scerri (2000). Chemical orbitals lie at the very core of structural chemical reasoning and share with students' alternative conceptions some elements; notably a good measure of classical “realism”. The paradoxical conclusion would be that in order to teach chemistry you cannot employ common chemical arguments.||

Ramsey (1997) happily called Folk Molecular Theory (FMT) the jumbled complex of ideas that informs the thought of chemists about the quantum realm. This unconventional mixture of classical and quantum concepts has proved solidly useful in guiding chemical practices for decades. The concept of orbitals as akin to classical physical objects is part of FMT, and it is instrumental in the way most chemists** think about molecular structure (for a more education-centered approach see, for example, Sánchez Gómez and Martín, 2003 or Taber, 2009; p. 236). In other words, if one gives up any a priori pretension of reducing chemistry to physics, chemical orbitals can be as legitimate a tool as any other in order to make sense of the molecular structure. The question would be then if such a conceptual approach is actually being taken by chemists, and, in particular, if it is the way chemical concepts are actually being taught. To probe into this, we shall focus on the above-mentioned idiosyncratic usage of orbitals through examples of their visual representation in the research and educational literatures.

It is not our aim in this perspective to make a thorough statistical analysis of the literature. Instead, we will assume that the answer to the previous question is yes, as a random walk through the literature, both technical and educational will show to the educated eye.

An appendix to this paper lists commented references to further examples, along with the criteria we have used to select those included in its body.

The visual dimension of science and science learning (Giere, 1996; Ramadas, 2009), and particularly chemistry (Hoffmann and Laszlo, 1991; Habraken, 1996, 2004; Weininger, 1998), has long been recognised as central to learning and research. It has been held that “visualization is of [models], and produces models” (Gilbert, 2005. See also Gilbert, 2008) and the development of models and their representations are crucial in the production of knowledge. Examples that go beyond the classic one of Kekulé and the benzene ring can be found in Hoffmann and Laszlo (1991). Markedly visual models also play central roles in the dissemination and acceptance of that knowledge: for example, that of the double helix of DNA has now reached iconic status, such that radically stylized versions of them are widespread and instantly recognized.

This quest for visualization has got into the very core of the realm of quantum chemistry, as evidenced by the appearance of the alleged first direct experimental picture of orbitals with the words “orbitals observed” in large bold letters in the front page of Nature (Humphreys, 1999, reporting Zuo et al., 1999).†† This is not a surprising situation since graphical representations, and in particular, pictorial descriptions of orbitals have been common in the chemical literature since the very beginning of quantum chemistry. Zuo's and later papers are relevant precisely because they have been read as revealing something that the chemists have known for a long time. Orbitals are shown as actual physical objects, which is the way most chemists use them in their everyday scientific practice. The fact is that the interpretation of all those results requires a good deal of quantum mechanics, and it is not at all obvious that they show orbitals as actual existing physical entities. See, for instance, Scerri (2002) and Mulder (2011).

In this paper we shall approach the usage of orbitals in visual representations employed in structural chemistry argumentations, showing through examples that, in this framework, they are used as physical objects, far from their mathematical origins.

Orbitals in chemical discourse

In the educational literature. Graphical representations of orbitals are easily found in any chemistry textbook (either general, organic or inorganic and even at the secondary education level). They are used both to represent structures and processes, the latter being even more relevant to our present purposes. Reaction mechanisms and bonding schemes are perhaps the most salient examples of these processes. They are also widely used in the research literature in a consistent way that is actually not essentially different from that of education and that comprises a small number of models of which more will be said later.

Mathematical versus “chemical” use: ontological change. In this subsection we shall present a series of examples of the way chemists usually employ orbitals in their structural reasoning. We shall focus on how the original mathematical meaning of the term “orbital” changes into something completely different.

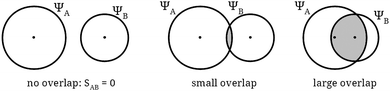
In some educational texts, graphical representations of orbitals are used to illustrate qualitatively a calculation that is explicitly performed. A particularly clear early example can be found in Fig. 3.5 of the widely influential book‡‡Valence, by Coulson (whose first edition dates from 1952) of which our Fig. 1 is a modern version.

Fig. 1 Overlap integral for two orbitals.

The purpose of this figure is to illustrate the rough features of the contribution of the overlap integral (S_AB in the figure) to the energy of a molecule. In a more quantitative way, similar images (see our Fig. 2, after Fig. 4 from Coulson, 1952) are used to support the verbal reasoning about the fact that the value of some of these overlap integrals is zero due to symmetry reasons.

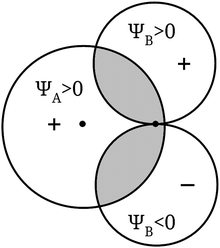Fig. 2 A diagram used to illustrate the vanishing of the overlap integral for symmetry reasons when Ψ_A is an s orbital and Ψ_B is a p orbital.

This kind of diagram is still used today in a very similar way. See e.g.Atkins (1992; p. 398) or Magnasco (2004). Nevertheless, in most cases, this close and explicit connection between the diagrams and the calculation is not present; therefore orbitals or, rather, their graphical representations might begin to acquire quasi-material status. Their interaction on the surface of the paper or the screen can be interpreted by learners as reflecting what actually happens to atoms and molecules.

This, which, as we shall see, is even clearer in animations, can be perceived in a typical example, which appears with very little variation in many texts, taken from a video lecture from the Coursera MOOC “Introductory Organic Chemistry – Part 1” (Moore et al. 2013). The fact that it is a lecture from a MOOC makes this example presumably close to actual classroom practice.

The objective of this short unit is to connect the language of frontier orbitals with the electron flows of classical chemistry. In the beginning, the instructor states that “reactions in organic chemistry can be described by the interaction of a filled orbital together with an empty orbital” and by the end, the role of orbitals is to act as mere receptacles for electrons acting as classical particles responsible for the formation of bonds via their electrical interactions. This is the sequence in which this transformation occurs:

1. (Fig. 3) The frontier orbitals (HOMO and LUMO) for the reaction BF₃ + NH₃ → F₃B − NH₃ are identified with the aid of a molecular orbital diagram.

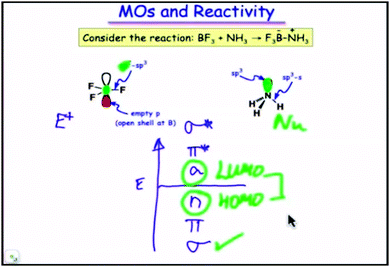Fig. 3 Molecular orbitals (HOMO and LUMO) in the reaction BF₃ + NH₃ → F₃B − NH₃. A still from time 4:03 in video lecture 4.11 from Moore et al. (2013).

2. At this point (Fig. 4) those orbitals are identified with the source and sink of a flow of electrons which is at the base of the classical arrow convention.

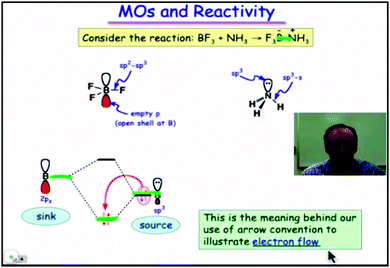Fig. 4 Frontier orbitals (HOMO and LUMO) identified as the source and sink of electrons. A still from time 4:32 in video lecture 4.11 from Moore et al. (2013).

3. Finally (Fig. 5), the connection with the curved arrow convention has been established. The orbitals disappear or rather are transformed into containers for electrons (source and sink; this had been hinted at from the beginning, since the talk of empty and filled orbitals) whose flow is what remains of orbital overlap. Arrows represent in classical terms the motion of electrons during the formation and breaking of bonds. From now on, the interaction of frontier orbitals can be visualized classically.

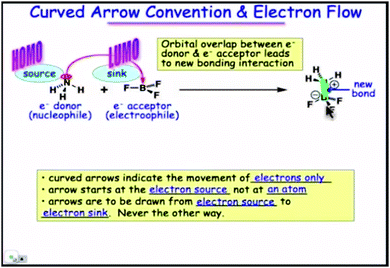Fig. 5 Frontier orbitals as electron containers (source and sink of flow). A still from time 5:07 in video lecture 4.11 from Moore et al. (2013).

It must be noticed that only a brief and rather simplified presentation of the quantum background of orbitals is provided in previous chapters.§§ This example and many others are presented without any explicit reference to a full quantum argument, which can only be the case, as the examples in fact clearly are beyond the set of physical systems available for a full quantum treatment.

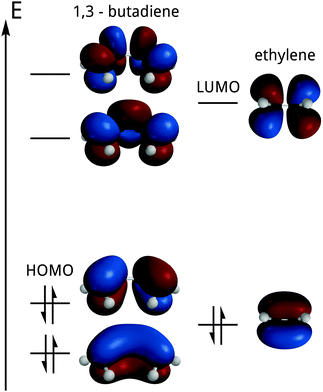
The education of most chemists does not include a rigorous approach to these techniques (Woodward–Hoffmann rules through perturbation theory, Hückel methods…) so, in the end, what is used and remembered is just the rules without the small print.¶¶ We find another such example in a popular introductory university chemistry textbook, Siska (2006), whose Section 18.5 is devoted to the Diels–Alder reaction|||| as an example of the use of molecular orbitals in the study of organic reactions. The Frontier Molecular Orbital Model*** is presented to “supplement, and in some cases replace the curly-arrow ‘electron pushing’ picture” (Siska, 2006, p. 700. The emphasis is ours).

The first figure of the section (Siska, 2006; Fig. 19.5, corresponding to our Fig. 6), superimposed on an energy diagram,††† depicts the most relevant orbitals (HOMO–LUMO and their closest neighbours) of the two molecules, whose reactivity is under study. Each of the two possible signs or phases is represented by a different colour.

Fig. 6 Frontier molecular orbitals (HOMO–LUMO) for butadiene and ethylene.

After identifying the HOMO and the LUMO, the phase (or sign) matching requirement for both orbitals is qualitatively introduced and applied to its interaction (see Fig. 7).

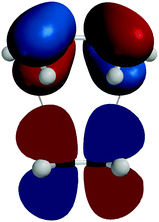Fig. 7 Interaction between the LUMO of ethylene and the HOMO of butadiene (corresponding to Siska, 2006, Fig. 19.6).‡‡‡

It should be noted that after orbitals have been introduced in simple cases and with all due caution§§§ in this textbook (Siska, 2006, ch. 3), they reappear almost exclusively through their boundary surfaces (which is common practice in many texts) in a way that conveys the idea of an identification between the orbital and its graphical representation as a well-defined region in space. Consequently, interactions between chemical species are ready to be reified as the overlapping and merging of those regions.

All of this is even clearer in two further examples. The first one, in a set of online lecture notes for an advanced general chemistry course taught at New York University (Tuckerman, 2011) which uses those same two figures. The text points at Fig. 7 stating that “The interaction between these orbitals is shown in the figure below. The figure illustrates that they must be combined so as to lead to constructive interference between the lobes”.

The second example can be found in the accompanying documentation for a laboratory exercise from the Chemistry and Biochemistry Department of the University of Colorado at Boulder (Fig. 8). Readers are told to “notice the favorable overlap (matching light or dark lobes)”.

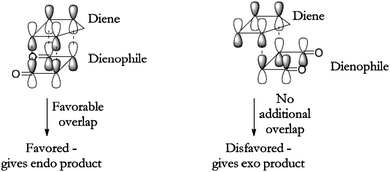Fig. 8 Molecular orbital theory explanation of the endo selectivity (University of Colorado at Boulder (n. d.)).

These examples show a line of reasoning strikingly similar to classical chemistry, where bond formation is due to interaction between the outer electrons of the reactant species even if, according to orthodox quantum mechanics, there is no correspondence between concrete electrons and orbitals due to the indistinguishability of identical particles.

In the research literature

To show that the usage of graphical representations of chemical orbitals is not restricted to the educational practice, but widespread in research as well, let's present a typical example (Kobori et al. 2009) from the J. Am. Chem. Soc. (Fig. 9):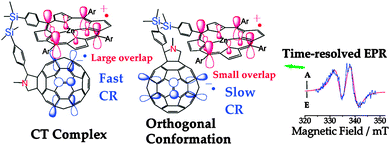

Fig. 9 For the formation of a complex (left), the overlap between SOMOs (Singly Occupied Molecular Orbitals) must be “large”. Reprinted with permission from Kobori et al. (2009; graphical abstract). Copyright 2009 American Chemical Society.

It is remarkable that this figure doesn't appear as such in the body of the paper, but in the journal index with graphical abstracts. This is another indication of the visual character of chemistry, which is being reinforced by the recent developments in computer science that make visualization and calculations easier than ever.

Scheme 1 in Maruyama et al. (2014) is another example of the usage of visual representations of chemical orbitals in research papers. Here, as in Fig. 4, orbitals are used as mere containers for electrons (represented as arrows) (Fig. 10):

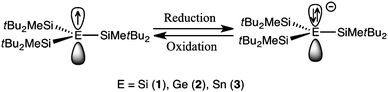Fig. 10 Reversible electrochemical anodic reduction–oxidation process of radicals 1–3 (Maruyama et al. 2014, Scheme 1).

Even in theoretical papers, such as Chen et al. (2014) can we find chemical orbitals visually represented. This final example features again orbitals as receptacles for electrons, whose motion is represented by a curved arrow (Fig. 11):

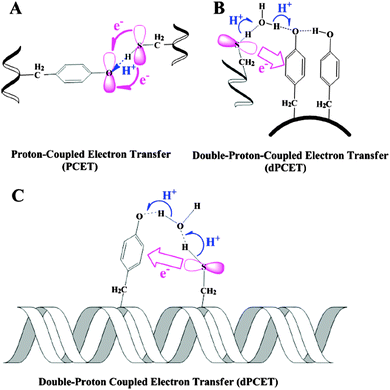Fig. 11 Different mechanisms for the proton/electron transfer reactions from Cys to Tyr˙ in proteins with various microstructures. Reprinted with permission from Chen et al. (2014; Scheme 1). Copyright 2014 American Chemical Society.

Animations in the graphical representation of mechanisms of bonding and chemical reactions

The two main themes in chemistry are, arguably, structure and reactivity and although the representation of the former via orbitals has remained essentially unchanged since the 1940s, the representation of processes is evolving rapidly thanks to the use of computer animations. Whereas paper only lends itself readily to the static representation of the initial and final states and perhaps some small number of discrete steps, computer animations showing a continuous time evolution make possible what we might call a narrative dimension that could change significantly its status, according to the studies in educational theory. See e.g.Avraamidou and Osborne (2009)¶¶¶ or Berger (2009, p. 55) for a wider perspective.

We can take as a representative example the formation of ethene starting from two methyl radicals as presented in the companion website|||||| of a well-known general chemistry textbook (Tro, 2007):

http://wps.prenhall.com/wps/media/objects/4974/<?ccdc_no 5093961?>5093961<?ccdc END?>/emedia/ch10/AAEDKKK0.html

As in previous examples, this animation shows the physical overlap of orbitals in the methyl radicals as the key in the formation of the new molecule, but now we can see how first the atomic orbitals change as the carbon atoms get closer (stage 1) into hybrid orbitals (stage 2), which then overlap, giving rise to the bonds which are responsible for the formation of ethene (Fig. 12).

Fig. 12 Formation of hybrid orbitals of carbon (right) from atomic orbitals.

It seems obvious to us that this animation does convey the impression that the formation of hybrid orbitals is an actual physical process somehow related to the proximity of two carbon atoms when all that can be said from the viewpoint of orthodox quantum chemistry is that hybrid orbitals are mathematical constructs built in order to fit to the known geometry of a molecule.****

As for the second part of the process (stages 3 and 4, in Fig. 13 below), the overlap that gives rise to sigma bonds is represented by little more than the juxtaposition of the newly formed hybrid orbitals. The lateral overlap giving rise to pi bonds is harder to depict, as it involves the yellow lobes representing hybrid orbitals that cannot touch in the previous step, so their interaction is suggested to occur by the appearance of a purple surface joining them.

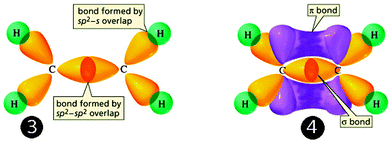Fig. 13 Overlap of hybrid orbitals leads to the formation of ethane. (Adapted from UC Davis' Chemwiki,†††† licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States License).

Animations like this one‡‡‡‡ are built out of static figures and are not very different from an ordered series of snapshots (the figures found in texts) joined by interpolation rather than by computing from a mathematical model; note the striking similarity between this last example and some figures from a high school textbook (Morcillo and Fernández, 1983) from which the authors, along with many Spanish scientists, learnt the rudiments of molecular structure in the 1970s and 1980s (Fig. 14).

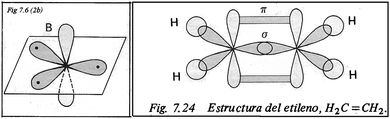Fig. 14 The structure of ethylene according to Morcillo and Fernández (1983) ©Editorial Anaya.

Conclusions

Figures and animations representing orbitals and their attendant concepts are ubiquitous in introductory texts, class notes and websites maintained by publishers, universities or teachers for advanced secondary and beginning university students and the same happens in the research literature for the relevant fields. Through them, students are exposed − in what for many will be their last contact with the subject in formal education − to a simplified, semi-classical and intuitive narrative which eludes the messy details of a series of models involving at times quite drastic approximations.

All of this makes at least plausible that the use of graphical representations described here could lead many of its “users” to feel that they are visualizing orbitals and their interactions “as they happen”, and as they happen in a “classical reality” at that. It can be argued whether this approach is correct or not, but the fact is that it is simply the way most chemists work, except for some quite narrow fields such as quantum chemistry. Chemistry education without chemical orbitals would not be about chemistry as it is usually practised.

Nevertheless, some of the characteristics of chemical orbitals would fall into the category of alternative conceptions or misconceptions to be overcome and which have even led to proposals of eschewing orbitals in chemical education altogether.

We are aware that our examples come from a variety of methods and that among them there is a wide range of levels of sophistication, but our point does not lie with their origin, but with their usage as chemical orbitals.

Our position is that often (as in the examples shown here) these chemical orbitals and their accompanying quantum concepts do not pose special difficulties; in contrast, their visual character may be an asset, so they must be present in chemical education.

Moreover, the usage of a quantum-like jargon is not, in fact, a flaw, but a lexical mannerism, an idiosyncratic feature of the language of chemistry. Every language, even artificial ones, has plenty of these loanwords. They are the sign of the historical becoming of the language, and they are digested into it to the extent that their origins are sometimes difficult to trace back. But the case of chemistry is particular, because many chemists do feel that they are using genuine physics when they employ concepts like ‘orbital’.

From the point of view of strict physicalism, the use of chemical orbitals and related concepts may not be acceptable, not even as an approximation. But the fact is that they are a time-honoured part of chemistry. We do not think that the role of science education is to set right the practice of its science, not even in the case of chemistry, easy-going, pragmatic and open to every influence as it is.

Acknowledgements

The authors would like to acknowledge the editor of this journal and one of the editors of the present themed issue (GT) for their help during the editorial process.

References

1. Atkins P. W., (1992), Physical Chemistry, 4th edn, Oxford University Press: Oxford.
2. Avraamidou L. and Osborne J., (2009), The role of narrative in communicating science, Int. J. Sci. Educ., 31(12), 1683–1707, DOI: http://10.1080/09500690802380695.
3. Berger J., (2009), About Looking, London: Bloomsbury Publishing.
4. Chang R. and Goldsby K., (2013), General Chemistry: The Essential Concepts, 7th edn, McGraw Hill: New York.
5. Chen X. et al., (2014), Water promoting electron hole transport between tyrosine and cysteine in proteins via a special mechanism: Double proton coupled electron transfer, J. Am. Chem. Soc., 136(12), 4515–4524, DOI: http://10.1021/ja406340z.
6. Coll R. K. and Taylor N., (2002), Mental models in chemistry: Senior chemistry students' mental models of chemical bonding, Chem. Educ. Res. Pract. Eur., 3(2), 175–184.
7. Coll R. K. and Treagust D. F., (2001), Learners' mental models of chemical bonding, Res. Sci. Educ., 31(3), 357–382.
8. Coulson C. A., (1952), Valence, 1st edn, Clarendon Press: Oxford.
9. Dicks A. P., (2001), Shake for sigma, pray for pi: Classroom orbital overlap analogies, J. Chem. Educ., 88(4), 426–427, DOI: http://10.1021/ed100002p.
10. Dirac P. A. M., (1929), Quantum mechanics of many-electron systems, Proc. R. Soc. London, Ser. A, 123(792), 714–733, DOI: http://10.1098/rspa.1929.0094.
11. Erduran S. and Scerri E., (2003), The Nature of Chemical Knowledge and Chemical Education, in Gilbert J., Jong O., Justi R., Treagust D. and Driel J. (ed.), Chemical Education: Towards Research-based Practice, Contemporary Trends and Issues in Science Education, Netherlands: Springer, vol. 17, pp. 7–27.
12. Giere R., (1996), Visual Models and Scientific Judgement, in Picturing knowledge: historical and philosophical problems concerning the use of art in science, University of Toronto Press: Toronto, p. 299 ff.
13. Gilbert J., (2005), Visualization: A Metacognitive Skill in Science and Science Education, in John Gilbert, (ed.), Visualization in Science Education, Models and Modeling in Science Education. Springer: Netherlands, vol. 1, pp. 9–27.
14. Gilbert J. K., (2008), Visualization: An Emergent Field of Practice and Enquiry in Science Education, in Gilbert J. K., Reiner M. and Nakhleh M., (ed.), Visualization: Theory and Practice in Science Education, Models and Modeling in Science Education, Springer: Netherlands, vol. 3, pp. 3–24.
15. Gillespie R. J., Spencer J. N. and R. S. Moog., (1996), Bonding and molecular geometry without orbitals - the electron domain model, J. Chem. Educ., 73(7), 622, DOI: http://10.1021/ed073p622.
16. Grossman R. B., (2003), The Art of Writing Reasonable Organic Reaction Mechanisms, Springer: New York.
17. Habraken C., (1996), Perceptions of chemistry: Why is the common perception of chemistry, the most visual of sciences, so distorted?, J. Sci. Educ. and Tech., 5(3), 193–201, DOI: http://10.1007/BF01575303.
18. Habraken C., (2004), Integrating into chemistry teaching today's student's visuospatial talents and skills, and the teaching of today's chemistry's graphical language, J. Sci. Educ. and Tech., 13(1), 89–94, DOI: http://10.1023/B:JOST.0000019641.93420.6f.
19. Hoffmann R. and Laszlo P., (1991), Representation in chemistry, Angew. Chem., Int. Ed. Engl., 30(1), 1–16, DOI: http://10.1002/anie.199100013.
20. Humphreys C. J., (1999), Electrons seen in orbit, Nature, 401(6748), 21–22.
21. Kobori Y. et al., (2009), Time-resolved EPR characterization of a folded conformation of photoinduced charge-separated state in porphyrin–fullerene dyad bridged by diphenyldisilane, J. Am. Chem. Soc., 131(5), 1624–1625, DOI: http://10.1021/ja8073775.
22. Magnasco V., (2004), A model for the chemical bond, J. Chem. Educ., 81(3), 427.
23. Maruyama H. et al., (2014), High-power electrochemical energy storage system employing stable radical pseudocapacitors, Angew. Chem., Int. Ed., 126(5), 1348–1352, DOI: http://10.1002/ange.201308302.
24. Moore J., Evans M. and Llewellyn N. M., (2013), Video lecture for unit 4.11 from Introductory Organic Chemistry – Part 1, University of Illinois at Urbana – Champaign, for Coursera, Instructor: Professor Jeffrey S. Moore. http://https://www.coursera.org/course/orgchem2a, Accessed 22 December 2013.
25. Morcillo J. and Fernández M., (1983), Química, Manuales de orientación universitaria, Anaya: Madrid.
26. Mulder P., (2011), Are orbitals observable? Hyle, 17(1), 24–35.
27. Papaphotis G. and Tsaparlis G., (2008a), Conceptual versus algorithmic learning in high school chemistry: The case of basic quantum chemical concepts. Part 1. Statistical analysis of a quantitative study, Chem. Educ. Res. Pract., 9(4), 323–331, DOI: 10.1039/B818468M.
28. Papaphotis G. and Tsaparlis G., (2008b), Conceptual versus algorithmic learning in high school chemistry: The case of basic quantum chemical concepts. Part 2. Students' common errors, misconceptions and difficulties in understanding, Chem. Educ. Res. Pract., 9(4), 332–340, DOI: 10.1039/B818470B.
29. Ramadas J., (2009), Visual and spatial modes in science learning, Int. J. Sci. Educ., 31(3), 301–318.
30. Ramsey J. L., (1997), Molecular shape, reduction, explanation and approximate concepts, Synthese, 111(3) 233–251.
31. Sánchez Gómez P. J. and Martín F., (2003), Quantum vs. “classical” chemistry in university chemistry education: a case study of the role of history in thinking the curriculum, Chem. Educ. Res. Pract., 4(2), 131–148.
32. Scerri E. R., (2000), The failure of reduction and how to resist disunity of the sciences in the context of chemical education, Sci. Educ., 9(5), 405–425, DOI: http://10.1023/A:1008719726538.
33. Scerri E. R., (2002), Have Orbitals Really Been Observed?, J. Chem. Educ., 79(3), 310, DOI: http://10.1021/ed079p310.1.
34. Simões A., (2004), Textbooks, popular lectures and sermons: The quantum chemist Charles Alfred Coulson and the crafting of science, Brit. J. Hist. Sci., 37(3), 299–342, DOI: http://10.1017/S0007087404005424.
35. Simões A., (2008), A quantum chemical dialogue mediated by textbooks: Pauling's the nature of the chemical bond and Coulson's Valence. Notes Rec. Roy. Soc., 62(3), 259–269, DOI: http://10.1098/rsnr.2007.0051.
36. Siska P. E., (2006), University Chemistry, Pearson Benjamin Cummings: San Francisco.
37. Smeenk C. T. L., (2013), A new look at the hydrogen wave function, Physics, 6, 58, DOI: http://10.1103/Physics.6.58.
38. Stefani C. and Tsaparlis G., (2009), Students' levels of explanations, models, and misconceptions in basic quantum chemistry: A phenomenographic study, J. Res. Sci. Teach., 46(5), 520–536, DOI: http://10.1002/tea.20279.
39. Stodolna A. S. et al., (2013), Hydrogen atoms under magnification: Direct observation of the nodal structure of Stark states, Phys. Rev. Lett., 110(21), 213001, DOI: http://10.1103/PhysRevLett.110.<?ccdc_no 213001?>213001<?ccdc END?>.
40. Taber K. S., (2002), Conceptualizing quanta: illuminating the ground state of student understanding of atomic orbitals, Chem. Educ. Res. Pract., 3(2), 145–158, DOI: 10.1039/B2RP90012B.
41. Taber K. S., (2004), Learning quanta: barriers to stimulating transitions in student understanding of orbital ideas, Sci. Educ., 89(1), 94–116, DOI: http://10.1002/sce.20038.
42. Taber K. S., (2009), Progressing Science Education: Constructing the Scientific Research Programme into the Contingent Nature of Learning Science, Springer.
43. Taber K. S. and Coll R., (2003), Bonding, in Gilbert J., Jong O., Justi R., Treagust D. and Driel J., (ed.), Chemical Education: Towards Research-based Practice, Contemporary Trends and Issues in Science Education, Springer: Netherlands.
44. Tro N. J., (2007), Chemistry: A Molecular Approach, Prentice Hall: Harlow.
45. Tsaparlis G., (1997), Atomic and molecular structure in chemical education: A critical analysis from various perspectives of science education, J. Chem. Educ., 74(8), 922, DOI: http://10.1021/ed074p922.
46. Tsaparlis G. and Papaphotis G., (2002), Quantum-chemical concepts: Are they suitable for secondary students? Chem. Educ. Res. Pract., 3(2), 129–144.
47. Tsaparlis G. and Papaphotis G., (2009), High-school students' conceptual difficulties and attempts at conceptual change: The case of basic quantum chemical concepts, Int. J. Sci. Educ., 31(7), 895–930, DOI: http://10.1080/09500690801891908.
48. Tuckerman M. E., (2011), CHEM-UA 127: Advanced general chemistry I. Lecture 17: Introduction to organic chemistry, http://www.nyu.edu/classes/tuckerman/adv.chem/lectures/lecture_17/node8.html, Accessed 22 December 2013.
49. University of Colorado at Boulder. (n. d.), Experiment 15. The Diels–Alder Reaction: Identification of an unknown dienophile, http://orgchem.colorado.edu/Labs/Experiments/Diels-Alder.pdf, Accesed 16 January 2014.
50. Weinberg S., (2003), Facing Up: Science and Its Cultural Adversaries, Harvard University Press: Cambridge.
51. Weininger S., (1998), Contemplating The Finger: Visuality and the Semiotics of Chemistry, Hyle, 4(1), 3–27.
52. Woody A. I., (2000), Putting quantum mechanics to work in chemistry: the power of diagrammatic representation, Philosophy of Science 67, Supplement. Proceedings of the 1998 Biennial Meetings of the Philosophy of Science Association. Part II: Symposia Papers: S612–S627.
53. Zuo J. M. et al., (1999), Direct observation of d-orbital holes and Cu-Cu bonding in Cu₂O, Nature, 401(6748), 49–52.

---

Footnotes

† And widely contested too. Erduran and Scerri (2003) touch upon this subject and its implications for education.

‡ In order to comply with the requirement of antisymmetry, the actual wave function is somewhat more complex. In quantum chemistry the usual way to introduce this is through a Slater determinant; a mathematical construction that preserves the norm of the wave function.

§ Though, as they say, “this is actually a mirage: though implicitly, many (most?) textbook authors and curriculum programmers are in favour of the use of orbitals for introducing chemical theory. For they include the issue not only in college chemistry courses, but even in the (upper) secondary education in many countries.”

¶ A tendency reinforced by classroom orbital overlap analogies such as “Shake For Sigma, Pray For Pi” (Dicks, 2001).

|| Note that we are not suggesting that students' alternative conceptions should be embraced, but the fact that they share some elements with chemical orbitals should surely be considered.

** Outside quantum chemistry departments.

†† The beginning of a series of such observations − many of them reported, for instance in Smeenk (2013) − of which the last might be that of Stodolna et al. (2013).

‡‡ Studied in depth by Simões (2004, 2008).

§§ Mainly in video lectures 1–12 (Moore et al. 2013) where the presentation stresses heavily the geometry of orbitals over their mathematical aspects.

¶¶ Approximate status, range of validity, exact technical meaning of all terms involved.

|||| A conjugate addition reaction of a conjugated diene to an alkene (the dienophile) to produce a cyclohexene. The simplest example is the reaction of 1,3-butadiene with ethane (ethylene) to form cyclohexene.

*** Summarily introduced earlier in their Section 7.2.

††† Analysed by Woody (2000) from a viewpoint not dissimilar to ours.

‡‡‡ Fig. 6 and 7 have been drawn by the authors from elements by Ben Mills in the public domain: http://commons.wikimedia.org/wiki/File:Butadiene-pi-MOs-Spartan-3D-balls.png.

§§§ i.e., According to standard elementary quantum mechanics.

¶¶¶ Though they define narrative rather narrowly as “fictional written text”, there are significant shared elements between those and animations.

|||||| http://wps.prenhall.com/esm_tro_chemistry_1/ Our example is Media 10.07, which can be found at http://wps.prenhall.com/wps/media/objects/4974/<?ccdc_no 5093961?>5093961<?ccdc END?>/emedia/ch10/AAEDKKK0.html, accessed 22 December 2013.

**** As Grossmann says in The Art of Writing Reasonable Organic Reaction Mechanisms (Grossmann, 2003): “organic chemists use the concept of atom hybridization to rationalize and understand molecular shape. The concept of hybridization is itself a strange hybrid of Lewis theory and molecular orbital (MO) theory, and there are serious questions about its basis in reality. Nevertheless, organic chemists use hybridization almost universally to rationalize structure and reactivity, because it is easy to understand and apply, and because it works!”

†††† UC Davis' Chemwiki: the Hybrid Orbital Model, available in http://chemwiki.ucdavis.edu/Under_Construction/chem1/Chemical_Bonding_and_Molecular_Structure/The_Hybrid_Orbital_Model, accessed May 2014.

‡‡‡‡ Or this, related to Chang and Goldsby (2013): http://www.mhhe.com/physsci/chemistry/animations/chang_7e_esp/bom5s2_6.swf

---