Morphologies and dynamics of linear ABC triblock copolymers with different block sequences

Abstract

The self-assembly behaviours, especially dynamic evolution, of linear ABC terpolymers with different block sequences are studied using a dissipative particle dynamic method. Except for several new morphologies, two different dynamic evolution mechanisms, “contacting and fusing” and “folding and fusing” are found for the first time.

---

Multicompartment micelles, originally proposed by Helmut Ringsdorf,¹ are one of most interesting morphologies for nanotechnology, in particular for nanobiotechnology.^2,3 Among several strategies for preparing them, the solution-state self-assembly of ABC terpolymers, which combine a hydrophilic and two mutually incompatible hydrophobic blocks, seems to be the most straightforward pathway.⁴ Due to tremendous advances in synthetic polymer chemistry,⁵ the preparation of ABC terpolymers with complicated multiblock architectures can be quite practical. Thus, in order to know what valuable ABC terpolymers should be synthesized, understanding the underlying principles governing their morphologies on the molecular level is of fundamental importance.

Traditionally, the concentric onion-like (core–shell–corona) micelles are regarded as the default structure adopted by ABC linear terpolymers (l-ABC),⁶ and ABC miktoarm star copolymers (μ-ABC) can effectively suppress the formation of concentric onion structures, leading to a fascinating array of new morphologies. Therefore, since the pioneer work by Lodge and co-workers,⁷ most investigations had been focused on the self-assembly of μ-ABC and various morphologies, such as worm, hamburger, and raspberry, are observed.⁴ Especially, a series of simulation and theoretical studies have also been performed to give a molecular-level understanding of the self-assembly of μ-ABC.⁸ Recently, the works of Laschewsky and co-workers reveal that l-ABC terpolymers with different block sequences can also form nonconcentric complex micelles.⁹ This is a inspiring result, because the relative ease synthesis of l-ABC might enhance their potential for commercial exploitation. However, comparing with μ-ABC, only a little simulation and theoretical works were paid attention to the self-assembly of l-ABC in solution.^8b,c,10

Despite extensive experimental efforts,⁹ the self-assembly of l-ABC in selective solvents still need an intensive exploration. However, the careful morphological visualization and dynamics process of complex micelles and the systematically study by experiments are still a very costly and time-consuming task. During the course of investigating μ-ABC, theory and simulation as paratactic tools with experiment show an outstanding position in the molecular-level understanding of the underlying principle.⁸ These principles are central to the engineering of new micelles with potentially enhanced properties and functions. Thus, it is very urgent that obtaining the comprehensive understanding of the self-assembly of l-ABC, especially the dynamics process, by means of theoretical or simulation methods.

Herein, we report an investigation of the self-assembly of linear triblocks with different block sequences (i.e. l-ABC, l-ACB and l-BAC) in solutions using dissipative particle dynamics (DPD), mainly considering the marked advance of this method in describing the dynamics evolution, and its details are given by Groot and Warren.¹¹ Relative comprehensive phase diagrams for linear triblocks in the dilute solutions are provided and several complex micelles, such as raspberry-onion-like, are predicted firstly. The influences of different block sequences on their dynamics evolution of self-assembly as an emphasis are investigated. Additionally, the dynamics process of self-assembly for the interesting raspberry-onion-like micelle is clearly shown. These works complement the existing experimental and theoretical results, leading to a more complete understanding of the self-assemble behaviour of l-ABC in solutions.

Our coarse-grained models for l-ABC (x-y-z) are consisted of the solvophilic block (A), the weakly solvophobic block (B) and the strongly solvophobic block (C), where x, y and z are the number of bead A, B and C, respectively. Adjacent beads in a chain are stringed by a linear spring with the harmonic spring constant of 4. The solvent is denoted by bead S. Their DPD repulsion parameters are listed in Table 1. The parameters are corresponding to describe the micelles of the famous miktoarm terpolymers μ-EOF⁷ and firstly used by Zhong et al.^8a,12 That is, B blocks of our model correspond to hydrophilic poly(ethylene oxide) blocks, A to lipophilic polyethylethylene blocks, and C to hydrophobic poly(perfluoropropylene oxide) blocks. Moreover, these parameters can also describe the strongly incompatible characteristic between these blocks. Lu and co-workers also used the same parameters to study the effect of chain topology on the morphology diversity of ABC terpolymers.^8c

Table 1 Repulsion parameters (DPD unit) in this work

	A	B	C	S
A	25	45	90	27
B	45	25	75	50
C	90	75	25	120
S	27	50	120	25

---

To avoid the finite size effects, a bigger cubic box of size (30r_c)³ containing 81 000 DPD beads is used. The volume fraction of l-ABC is 0.1 to guarantee the dilute solution. For convenience, the cutoff radius, the particle mass, and the temperature are all taken as unity, i.e. r_c = m = k_BT = 1. The time step Δt is 0.05 and a total of 2 × 10⁶ DPD time steps are carried out to guarantee the equilibration for each system.

The detailed morphological phase diagrams for l-ABC, l-ACB and l-BAC are shown in Fig. 1 and Fig. S1–S6,† respectively. For l-ABC, the whole phase diagrams have been reported by our previous work.¹³ Here, we further give the phase diagrams for the l-ACB and l-BAC, and focus on the effects of block lengths on the phase transition. As shown in Fig. 1 and ESI,† several predicted new and interesting morphologies are given. For example, raspberry-onion (2-12-2), cage (2-8-8) and bowl (8-8-2) micelles of l-ABC, cylindrical raspberry (2-12-2) and worm raspberry (4-4-8) of l-ACB, multicore-worm (2-2-2) and connected raspberry (8-2-2, 12-2-2) of l-BAC, and so on. Secondly, several basic principles on the morphological transition are also summarized based on the phase diagrams. Increasing the length of solvophilic A blocks can result in the formation of dispersive small micelles. These small micelles generally keep the initial morphologies of the self-assemble process, such as the three-layer “hamburger” structure. This is simply understood, because the longer solvophilic A blocks have enough ability to form the relative whole barrier on the surface of the solvophobic aggregates and prevent the direct interaction between the solvents and the solvophobic blocks. As for the solvophobic B and C blocks, we can discuss their effects in terms of the variation of block ratios. When y/z increases, B blocks prefer to form the bigger sphere and C blocks become the patches embedding into the surface, and vice versa. Moreover, a slight of differences in morphologies are distinguished based on the different block sequences, such as raspberry-onion-like micelle of l-ABC (2-12-2), cylindrical raspberry of l-ACB (2-12-2) and connected raspberry of l-BAC (12-2-2). The thermodynamics explanations for these morphological differences had been mentioned.^8b,c Here, the morphologies from our simulations is also determined by the free energy. The ideal shape is the common spherical micelle with C core and A shell surrounded by B corona. The variation of block length can result in the delicate balance between the benefit of interfacial energy and the energy penalty, which determine the final equilibrium structures. In fact, the underlying dynamics process analysis for multicompartment micelles is given little attention. Thus, in this paper we lay a lot of emphasis on the dynamics evolution of multicompartment micelles from the self-assembly of linear triblocks.

Fig. 1 Morphological phase diagrams of linear triblocks with different block sequences. The solvophilic block (A) is red and selectively omitted for clarity, the weakly solvophobic block (B) is blue and the strongly solvophobic block (C) is green. The solvent (S) is not shown for clarity.

Taking l-ABC, l-ACB and l-BAC with x = y = z = 2 as examples, the effects of block sequences on the dynamics process are investigated and the results are given in Fig. 2. As early as the initial stage (t = 100), the three triblocks copolymers assemble into the different building units, i.e. two-layer “ring” for l-ABC, three-layer “hamburger” for l-ACB and multi-layer for l-BAC. Then, the discrete units of l-ABC and l-ACB undergo a similar process of “contacting and fusing” and finally form the onion-like and bicontinuous micelles, respectively. The detailed processes are that the triblocks firstly formed discrete building units, and then they approached each other until contact, followed by the fusion. The similar process is also found for the miktoarm star terpolymers.^8a During the “fusing” stage, a little difference can be distinguished. For l-ABC, the B shells firstly contact each other and open a protective passageway for the aggregation of C cores. For l-ACB, its fusion is to the simultaneous touching of B and C cores. However, l-BAC shows an alternative mechanism. The multilayer units rapidly fit together by “head to tail”, not “shoulder to shoulder”, and become longer worm-like micelles, followed by the interesting process of “folding and fusing”. Details of this evolution process are that the threadlike micelles firstly curled and formed a loop, then they approached each other and progressively aggregated a thick multicore cylindrical-micelle. This interesting morphology is also found in experiments of μ-EOF⁷ and theoretical studies on the self-assembly of l-ABC in midblock-selective solvents.¹⁰ Wang and Lin¹⁰ also provide a valuable distinguish between the common multicompartment micelle and the multicore micelle. Moreover, we can see that, in the “fusing” stage, the weakly solvophobic B blocks always merged together before the strongly solvophobic C blocks. In Fig. S2–S4,† several triblocks, such as l-ABC (8-8-8), l-ABC (8-4-8, 8-8-8) and so on, form the similar worm-like micelles, however, do not undergo the dynamic evolution of “folding and fusing”. It clearly testifies the different influence of block sequences.

Fig. 2 Dynamics evolution of l-ABC, l-ACB and l-BAC with x = y = z = 2, respectively. Color scheme in the snapshots: A (red), B (blue), C (green).

In addition, the interesting and novel raspberry-onion-like micelle formed by l-ABC (2-12-2) is investigated alone. Fig. 3a gives the detailed size of raspberry-onion micelle. Just looking from the outside, the micelle shows the raspberry-like morphology, which can also be formed by linear PVBM-PS-PVBFP triblock copolymers^9a and μ-EOF miktoarm star terpolymers.¹⁴ For the coupling raspberry and onion structure, Zhong et al. also found the similar micelle from the self-assembly of linear ABC and star ABC terpolymers blends.¹² The diameter of the whole micelle is about 160 (DPD unit), and that of inner core is 50 and one-third of the whole micelle. The interfacial embedded cores have an average diameter of about 22. The ratio between the embedded cores and the whole micelle is slightly smaller than that of raspberry-like micelle labeled by Laschewsky et al.^9a If the central core is not detected effectively by experimental means, this structure would be regarded as a popular raspberry-like micelle. In that way, the micelle should has a diameter of 110 (DPD unit) and it is very difficult to explain the extra length of 50 (DPD unit). To understand the formation of the crucial inner core, Fig. 3b shows the evolution of the self-assembly of l-ABC (2-12-2). It firstly forms several small “raspberry”, which develop according to the mechanism of “contacting and fusing”. During the fusing course, several small C cores wander into the interior of the bigger B sphere (denoted by the glazed density surface) and then aggregate a large core by the fusion. We have to recognize that the experimental means are difficult to obtain this type of dynamic process.

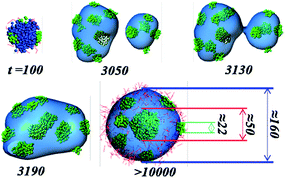Fig. 3 Dynamics evolution and detailed sizes in DPD unit for the special raspberry-onion-like micelle formed by l-ABC (2-12-2). Color scheme in the snapshots: A (red), B (blue), C (green).

Conclusions

DPD simulation method is used to give insight into the self-assembly of linear ABC triblock copolymers with different block sequences in the selective solvents. Detailed phase diagrams are provided and several new morphologies beyond the past knowledge are predicted, such as raspberry-onion, ring, and so on. The most importance is that the effects of block sequences on the dynamic process of the aggregation of linear triblocks are investigated. Two different mechanisms, i.e. “contacting and fusing” for l-ABC and l-ACB, and “folding and fusing” for l-BAC, are founded by distinguishing several obvious differences in the evolution. The results in this work primarily provide the valuable knowledge for the complex morphologies of linear triblocks with different block sequences based on the dynamic evolution.

Acknowledgements

All the authors appreciate very much the financial support from CAEP Foundation (no. 2014B0302040 and 2014-1-075) and National Nature Sciences Foundation of China (no. 11402241). Thanks Dr HongGang Xia for the valuable discussions. Authors are also grateful to editors and reviewers for their effective work.

Notes and references

1. H. Ringsdorf, P. Lehmann and R. Weberskirch, Multicompartmentation – a concept for the molecular architecture of life, in 217th ACS National Meeting, Anaheim, CA, 1999.
2. L. Zhang and A. Eisenberg, Science, 1995, 268, 1728.
3. C. Zhou, M. A. Hillmyer and T. P. Lodge, J. Am. Chem. Soc., 2012, 134, 10365.
4. (a) A. O. Moughton, M. A. Hillmyer and T. P. Lodge, Macromolecules, 2012, 45, 2; (b) A. Laschewsky, Curr. Opin. Colloid Interface Sci., 2003, 8, 274.
5. C. J. Hawker and K. L. Wooley, Science, 2005, 309, 1200.
6. N. Hadjichristidis, H. Iatrou, M. Pitsikalis, S. Pispas and A. Avgeropoulos, Prog. Polym. Sci., 2005, 30, 725.
7. Z. Li, E. Kesselman, Y. Talmon, M. A. Hillmyer and T. P. Lodge, Science, 2004, 306, 98.
8. (a) J. Xia and C. Zhong, Macromol. Rapid Commun., 2006, 27, 1110; (b) S. H. Chou, H. K. Tsao and Y. J. Sheng, J. Chem. Phys., 2006, 125, 194903; (c) Y. Zhao, Y. T. Liu, Z. Y. Lu and C. C. Sun, Polymer, 2008, 49, 4899; (d) E. B. Zhulina and O. V. Borisov, Macromolecules, 2008, 41, 5934; (e) W. Kong, B. Li, Q. Jin, D. Ding and A. C. Shi, J. Am. Chem. Soc., 2009, 131, 8503; (f) S. Li, Y. Jiang and J. Z. Y. Chen, Soft Matter, 2013, 9, 4843.
9. (a) M. Kubowicz, J. F. Baussard, J. F. Lutz, A. F. Thunemann, H. von Berlepsch and A. Laschewsky, Angew. Chem., Int. Ed., 2005, 44, 5262; (b) H. von Berlepsch, C. Bottcher, K. Skrabania and A. Laschewsky, Chem. Commun., 2009, 17, 2290; (c) K. Skrabania, A. Laschewsky, H. von Berlepsch and C. Bottcher, Langmuir, 2009, 25, 7594; (d) K. Skrabania, H. von Berlepsch, C. Bottcher and A. Laschewsky, Macromolecules, 2010, 43, 271; (e) J. N. Marsat, M. Heydenreich, E. Kleinpeter, H. von Berlepsch, C. Bottcher and A. Laschewsky, Macromolecules, 2011, 44, 2092.
10. L. Wang and J. P. Lin, Soft Matter, 2011, 7, 3383.
11. R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423.
12. J. Xin, D. Liu and C. Zhong, J. Phys. Chem. B, 2009, 113, 9364.
13. Y. Zhou, H. G. Xia, X. P. Long, X. G. Xue and W. Qin, Macromol. Theory Simul., 2014 DOI:10.1002/mats.201400072.
14. Z. Li, M. A. Hillmyer and T. P. Lodge, Langmuir, 2006, 22, 9409.

---

Footnote

† Electronic supplementary information (ESI) available: Additional phase diagrams. See DOI: 10.1039/c4ra13814g

---