Acid base co-crystal converted into porous carbon material for energy storage devices

Abstract

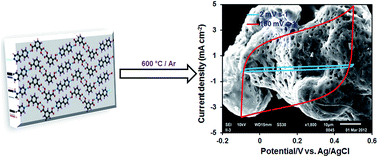
A simple and facile method is adopted for the synthesis of pure and catalyst free carbon material for supercapacitor applications. In a co-crystal synthesis, the precursors (isophthalic acid and a base, 4,4′-bipyridine) are arranged in regular pattern, followed by carbonization at 600 °C under an inert atmosphere to produce pure carbon material, CIN-600. The obtained sample is characterized by many techniques, such as powder X-ray diffraction (PXRD), transmission electron microscopy (TEM), scanning electron microscopy (SEM), energy dispersive X-ray spectroscopy (EDS), and gas adsorption analysis. The gas adsorption and microscopic analysis demonstrated the high porosity of the carbon sample and its irregular geometry. Owing to the excellent porosity and electrical conducting properties, CIN-600 showed enhanced capacitive performance when used as an electrode material in electric double layer capacitors. The specific capacitance of the sample was ca.181.3 F g⁻¹ at 2 mV s⁻¹ and maintained 91.3% of its initial capacitance in a long-term cycling test.

---

Introduction

Co-crystals are solid materials under ambient conditions. Co-crystals comprise two or more molecules, known as co-crystal constructors. According to a Cambridge Structural Database (CSD) survey, co-crystals represent less than 0.5% of the published crystal structures.¹ Co-crystals can be easily synthesized by invoking their molecular structure and molecular interactions, such as hydrogen bonding, between the co-crystal constructors. So far, co-crystal synthesis has been limited to photopolymerization and nucleophilic substitution,² where their potential impact on pharmaceutical formulation and green chemistry is significant.

In the present study, for the first time, we present the application of a co-crystal in the synthesis of pure, catalyst-free, cost-effective and porous carbon material. The co-crystal (In-3) was synthesized from two co-crystal constructors: isophthalic acid (1,3-benzenedicarboxylic acid) and 4,4′-bipyridine. The In-3 was structurally characterized by X-ray single crystal analysis, and it was found that in In-3, the constructors are arranged in polymeric chains via hydrogen bonding.

Supercapacitors, or electric double-layer capacitors (EDLCs), are modern electronic devices that work on the principle of double-layer capacitance at the electrode/electrolyte interface, where electric charges are accumulated on the electrode surfaces and oppositely charged ions are arranged at the electrolyte side. EDLCs are superior over modern secondary batteries because of their potential applications in high power output and high energy density appliances. Supercapacitors are used in electronic equipment where a demanding power supply, high current drain is required and for work under extreme environmental conditions.³ The electrodes of supercapacitors consist of different carbon materials, such as carbon nanotubes (CNTs),⁴ graphene,⁵ activated carbon,⁶ carbon onion,⁷ carbon fibers,⁸ and mesoporous carbon.⁹ These carbon materials should be predominantly porous in nature to ensure a proper accommodation of the electrolyte ions. The surface area and porosity depends on the synthesis process and the nature of the carbon precursor. Different sources, such as metal carbides,^10–12 polymers,¹³ natural gas,¹⁴ natural silk,¹⁵ sucrose,¹⁶ furfuryl alcohol,¹⁷ and metal–organic frameworks (MOFs)^18–20 etc. have been used for the synthesis of carbon materials.

Among the different methods, carbonization or template carbonization^21–28 is one of the synthetic routes used in which the carbon material could be obtained by heating the carbon source precursor at elevated temperatures. However, this method suffers due to the complex polymerization process at elevated temperature; the need for careful selection of the proper template, which sometimes leads to the contamination of the final product; the need for an acid wash of the product to remove the metal/metal oxide derived from the template or catalyst; and its low experimental yield. To address these limits, there is a need for a suitable carbon source and a facile synthetic route.

In the present study, we report a simple and facile method for the synthesis of carbon material via carbonization of a solid-state co-crystal at 600 °C. To the best of our knowledge, no report has yet been published where the carbon material is derived from co-crystals. The co-crystals were synthesized under solvothermal conditions and characterized. The synthesized carbon material was tested as an electrode material in a supercapacitor.

Experimental

Synthesis of the co-crystal (In-3)

In-3 was synthesized by mixing solutions of isophthalic acid (IPA) (1.0 mmol) and 4,4′-bipyridine (Bipy) (0.5 mmol) in a 20% ethanol solution of water, then stirred and introduced into a Teflon-lined autoclave, which was kept at 120 °C for 24 h, followed by slow cooling to obtain yellow crystals. The product was filtered, washed with water and ethanol, and then dried under vacuum. Yield: 79%, Anal. calcd: C, 63.93% H, 4.13%, N, 5.74% found: C, 63.84% H, 4.06% N, 5.61. IR data (ν_max/cm⁻¹): 3447 mbr, 3077 s, 1612 s, 1549 m, 1533 s, 1421 s, 1263 m, 1252 s, 1237 s, 1177 s, 1141 m, 1051 m, 1041 m, 976 s, 968 m, 866.

Pyrolysis of In-3

The In-3 (0.5 g) was ground to a fine powder and transferred into a ceramic boat, which was then placed in a quartz tube fixed in a tube furnace (Nabertherm B 180). Air was flushed away by a continuous flow of Ar for 30 min. The sample was heated up to 600 °C (10 °C min⁻¹) for 6 h under a continuous flow of Ar gas and then cooled slowly to room temperature. The carbon material (0.33 g) obtained was denoted as CIN-600 and had a total yield of 66%.

Characterization

The single crystal X-ray diffraction data was collected on a Bruker kappa APEXII CCD diffractometer using graphite-monochromator Mo-Kα radiation (λ = 0.71073 Å) at ambient temperature. For the data collection, ω scan and multi-scan absorption corrections were applied. A final refinement on F2 was carried out by a full-matrix least-squares technique. The structural solution and refinements were accomplished with SHELXL-97,²⁹ WinGx,³⁰ SAINT,³¹ and PLATON³² software. Wide angle X-ray diffraction measurements were carried out at a speed of 0.015 s⁻¹ by a PANalytical diffractometer (X'Pert PRO 3040/60) with a Cu Kα (λ = 1.544206 Å) radiation generated at 40 kV and 30 mA. The surface morphology of CIN-600 was examined by a scanning electron microscope (JEOL-JSM-6610LV) equipped with an energy dispersive X-ray spectroscope (EDS). A TEM analysis of the sample was conducted with FEI Company's Titan 80-300 CT transmission electron microscope with an acceleration voltage of 300 kV. N₂ adsorption/desorption measurements were carried out using the Accelerated Surface Area & Porosimetry System 2020 supplied by Micromeritics Instruments Inc. Approximately 20 mg of sample was loaded into a glass analysis tube and outgassed for 3 h under vacuum at 200 °C prior to measurement. The isotherm was measured at 77 K and the resulting data was analyzed using Bruner–Emmett–Teller (BET)'s model to determine the surface area. The pore size distribution plot was conducted on the adsorption branch of the isotherm based on the density functional theory (DFT) model. FT-IR analysis was carried out on a Thermoscientific NICOLET 6700 FTIR.

Electrochemical studies

For the electrode preparation, a black slurry was prepared by mixing 5 mg of CIN-600 with 5 mL of ethanol and 10 μL of Nafion (5 wt%) solution which was then sonicated for 30 min. After evaporating off the ethanol, the black slurry was pressed between two pieces of nickel foam (1 cm × 1 cm) under a pressure of 350 kg cm⁻² (using the hydraulic presser EQ-HP-88V220). After drying at 100 °C, the electrode was impregnated with the electrolyte solution overnight to ensure complete saturation of the electrode materials with electrolyte ions. The designed electrode was subjected to the electrochemical studies in a three-electrode cell assembly using 6 mol L⁻¹ KOH. The cell assembly consisted of the CIN-600 sample electrode as the working electrode, platinum wire as the auxiliary electrode, and Ag/AgCl as the reference electrode. All the electrochemical measurements were carried out with a Biologic SP 300 electrochemical analyzer at room temperature.

Results and discussions

Characterization

The single crystal X-ray structural analysis of In-3 is presented in Fig. 1, and the crystallographic data and structure refinement parameters are tabulated in Table S1 (ESI†).

Fig. 1 (a) Asymmetric unit of the co-crystal In-3, (b) molecular structure of the In-3, consisting of two acids and one base molecule, (c) 2D sheet of In-3 formed by inner-tape CH⋯O type hydrogen bonding and the zigzag tape structure of In-3 formed by the intermolecular OH⋯O and OH⋯N type hydrogen bonding.

The crystal structure reveals that In-3 was formed by the coupling of IPA and Bipy in a 2 : 1 ratio (see Fig. 1(b)). In In-3, two IPA molecules were coupled by OH⋯O type hydrogen bonding and formed a six-member planar ring, and this pair then form an OH⋯N type hydrogen bond with Bipy, which leads to a zigzag tape structure. CH⋯O type hydrogen bonding assembles these zigzag tapes into a sheet structure (see Fig. 1(c)). A similar type of co-crystal structure has been reported by Shan et al.^33,34 The layer-by-layer packing of 2D sheets in the crystal packing motivated us to carbonize the co-crystal in order to obtain an ordered carbon material.

The PXRD pattern of CIN-600 revealed the formation of pure carbon material. The heteroatoms, such as N and O, in the In-3 were converted into NO_x, O₂, and CO_x and then vaporized in an Ar flow environment. Broad peaks at 2θ = 25° and 2θ = 45° in the XRD pattern of CIN-600 (see Fig. 2) correspond to the (002) and (100) crystallographic planes of carbon material. To evaluate the degree of graphitization, the empirical parameter (R) was used, which can be defined as the ratio of the height of the (002) Bragg peak to the background.^25,26 The R factor for the CIN-600 sample is 0.62, which shows that some graphitic sheets are also present along with other types of carbon matrix.

Fig. 2 Powder XRD pattern of CIN-600.

To evaluate the surface area and the pore size distribution, a N₂ adsorption/desorption analysis was performed and the isotherm is shown in Fig. 3. A type-IV isotherm was found for the CIN-600 sample, suggesting the existence of different pore sizes ranging from micropores to mesopores. At a high relative pressure, hysteresis between the adsorption and desorption branches demonstrates the presence of mesopores in the surface texture. The BET surface area of the CIN-600 sample is 1230 m² g⁻¹, with a pore diameter of 2.13 nm.

Fig. 3 N₂ adsorption/desorption isotherm and pore size distribution (inset) of the CIN-600 carbon sample.

To characterize the surface morphology of the sample, TEM and SEM analyses were conducted and the obtained images are presented in Fig. 4. The TEM images (see Fig. 4(a and b)) show the microporous nature of amorphous carbon. It is obvious that the surface texture of the samples is porous with a monolithic irregular shape. The SEM images of the CIN-600 sample (see Fig. 4(c and d)) show that clear and well-defined pores were created at the surface during fabrication of the CIN-600 carbon sample. These pores and the ruptured surface are developed by the exclusion of gases like CO_x and NO_x during carbonization under the Ar atmosphere. The porosity of the carbon material has a very important role to play in the capacitance of a capacitor. Carbon material with a proper pore size and distribution is required for good capacitive performance. The pores of the carbon material can facilitate the inside diffusion of ions during charge–discharge operating conditions. In the present study, the CIN-600 sample exhibited good capacitive performance due to the porous nature, as was evident from the gas adsorption and microscopic analyses. An EDX analysis was carried out to confirm the per cent composition and purity of the CIN-600 sample. FT-IR analysis also supports the purity of the carbon material (see Fig. S1†). The EDX spectrum has (see Fig. 4(e)) a single point at 0.25 keV for carbon, which suggests a high purity of the obtained sample.

Fig. 4 TEM micrographs (a and b), SEM images (c and d) and EDX spectrum of CIN-600 (e).

Electrochemical evaluation

The working principle of a supercapacitor is the accumulation of electrolyte ions in the electric double layer developed by the electrostatic force. The capacitance (energy stored by electrode) largely depends on the surface interaction of the electrode and electrolyte. There is a direct relationship between the specific capacitance and surface area: C_sp = εS/d; where C_sp = specific capacitance, ε = permittivity of electrolyte, S = surface area of the electrode–electrolyte interface, and d = distance between the polarized carbon surface and the maximum charge density of solvated ions.^27,28 However, only the surface that can be electrochemically accessed by the solvated ions contributes to the capacitance. The pore size of the electrode materials should be properly matched with the size of the solvated ions for excellent capacitive performance. In addition, the capacitance of a capacitor also depends on the surface wettability, the applied pressure for packing, and the electrical conductivity of the electrode materials.

The voltammograms of the CIN-600 sample are presented in Fig. 5(a) with different voltage scan rates from 2 mV s⁻¹ to 150 mV s⁻¹ in the potential range of −0.1 V to +0.5 V. The sample has excellent capacitive behavior, as is obvious from the fairly rectangular shape of the voltammograms in the given range of the potential scan rates. The box-like rectangular shape of the voltammograms with the increasing voltage sweep rate suggests that the electrode material is quite suitable for quick charge–discharge operation conditions. Generally, a better capacitive behavior of a sample at high voltage sweep rate is attributed to a better accessibility of the ions to the electrochemically active surface area. It is believed that the capacitive performance of the carbon materials depends on the pore size, which favors the penetration of solvated ions. The excellent capacitive performance of the CIN-600 sample can also be attributed to its large porosity, as presented in the gas adsorption and microscopic studies. The specific capacitance (F g⁻¹) from the CV curves were calculated using the following equation; C_sp = (ΔQ)/(ΔV × m); where ΔQ is the charge (C) integrated from the whole voltage range, ΔV is the whole voltage (V) difference, and m is the mass (g) of carbon on the electrode. The calculated values of the specific capacitance are given in Table S2 (ESI†) for the CIN-600 sample. As can be seen in the data, the CIN-600 sample has the highest capacitance of 181.3 F g⁻¹ at a sweep rate of 2 mV s⁻¹ and the lowest capacitance value of 122.3 F g⁻¹ at a voltage sweep rate of 150 mV s⁻¹. At low sweep rates, the ions have sufficient time to diffuse into the pores of the sample, while at high voltage scan rates, the ions can only penetrate into some external large pores by a rapid movement.

Fig. 5 Cyclic voltammetric curves at different potential sweep rates (a), galvanostatic charge/discharge curves at different current densities (b), plot of retained capacitance versus scan rates (c), and long-term cycling (d) of the CIN-600 sample.

The relationship between the ratio of the retained capacitance and the voltage scan rate is plotted and presented in Fig. 5(c). There is a decrease in the ratio of the retained capacitance with increase in the voltage scan rate, showing the limited use of the electrochemically active surface area at high scan rates in comparison to at low scan rates. However, the sample retains about 66% of its initial capacitance, even at a high scan rate of 150 mV s⁻¹.

Galvanostatic charge/discharge tests were also carried out in the potential window of −0.1 V to +0.5 V at different current densities from 0.250 A g⁻¹ to 1.5 A g⁻¹ in order to evaluate the capacitive performance of the carbon material, and the results are shown in Fig. 5(b). The specific capacitance was calculated by the equation; C_sp = (I × Δt)/(ΔV × m), where I is the constant discharge current, Δt is the discharge time, ΔV is the voltage difference, and m is the mass of the carbon material. The specific capacitance from the charge/discharge measurements at different current densities are given in Table S2.† It is clear that the charging curve is almost symmetrical with their corresponding discharge counterpart, and furthermore, the linear voltage–time relationship having no obvious voltage drop indicates the good capacitive behavior of the CIN-600 carbon sample. The galvanostatic charge/discharge results are consistent with the voltammetric measurements, illustrating an ideal capacitor behavior. The cycling charge/discharge measurements were conducted at 0.500 A g⁻¹ to test the long-term cycling stability of the carbon electrode material (see Fig. 5(d)). The CIN-600 sample maintains almost 91.3% of its initial capacitance after 3000 cycles, presenting its good long-term cyclic stability. Fig. 6 shows that the voltammetric currents are almost proportional to the scan rate of the CV. The slop of the i–υ lines is dependent on the measured potential. The linear dependency of the current on the scan rates of the CV illustrates the high-power characteristics of the CIN-600 sample.

Fig. 6 Plot of current density versus potential scans rates (i–υ) from the CV results, where the current (anodic) was obtained at: 0.0 V, 0.2 V, and −0.4 V.

The electrochemical performance of CIN-600 is comparable with most of the recently reported porous carbon materials synthesized by complicated and time-consuming processes. A few reports are described here for reference. Lu et al. obtained ordered mesoporous carbon (OMCs) from sucrose with controllable pore sizes in the range of 4–10 nm by a template procedure, using 2D hexagonal MSU-H and 3D cubic KIT-6 silica as hard templates and boric acid as the pore expending agent. The prepared OMCs exhibited specific capacitance values from 143 F g⁻¹ to 205 F g⁻¹ at 5 mV s⁻¹.³⁸ Li et al. synthesized nitrogen enriched microporous carbon spheres (MCS) by the polymerization-induced colloid aggregation method with a BET area of 1330 m² g⁻¹. As an electrode material for electric double-layer capacitors, the MCS have shown a specific capacitance value of 211 F g⁻¹ at a discharge current density of 1 A g⁻¹.³⁹ Song and coworkers prepared phenolic-based carbon nanofiber webs (PCNFWs) by electrospinning a resole-type phenolic resin/PVA blend solution, followed by curing and carbonization.⁴⁰ The specific surface area of the carbon was 416 m² g⁻¹ and specific capacitance values up to 171 F g⁻¹ at 5 mV s⁻¹ were obtained. Jin and coworkers⁴¹ have reported novel carbon-based microporous nanoplates containing numerous heteroatoms (H-CMNs) from regenerated silk fibroin. The BET surface area of the carbon product was 2557.3 m² g⁻¹, similar to pristine graphene sheets. The H-CMNs exhibited a specific capacitance up to 264 F g⁻¹ at 0.1 A g⁻¹ current density in 1 mol L⁻¹ H₂SO₄. Guo et al.⁴² prepared microporous carbon materials by the carbonization of sulfuric acid-pretreated sucrose. The pore size and BET surface area were in the ranges of 0.7–1.2 nm and 178–603 m² g⁻¹, respectively. It was concluded that the sample carbonized at 800 °C displayed the highest surface area and highest specific capacitance of 232 F g⁻¹ at 0.1 A g⁻¹ current density. Xu and coworkers⁴³ used a metal–organic framework (MOF) as a template and furfuryl alcohol as a precursor for the synthesis of nanoporous carbon (NPCs). The BET surface area of the NPCs fall in the range of 1140 m² g⁻¹ to 3040 m² g⁻¹ and the pore size distribution was centered at about 3.9 nm. They concluded that the NPC samples obtained at a temperature higher than 600 °C have constant specific capacitance up to 100 F g⁻¹ at 5 mV s⁻¹, while the NPC sample obtained at 530 °C gives rise to a specific surface area of 3040 m² g⁻¹, but a lower specific capacitance of 12 F g⁻¹ at 5 mV s⁻¹.

The electrochemical behavior of the carbon sample CIN-600 was further evaluated by impedance spectroscopy. Generally, the Nyquist spectrum is divided into a high frequency semicircle region attributed to the charge transfer resistance occurring at the electrode/electrolyte interface and a low frequency curve with a 45° slope, representing the Warburg diffusion resistance.³⁵ The impedance study of the CIN-600 carbon electrode in 6 mol L⁻¹ KOH solution in the frequency range of 1 Hz to 100 000 Hz (at 10 mV as the potential amplitude) is shown in Fig. 7. The Nyquist plot (see Fig. 7(a)) consists of two parts, the horizontal line (with real axis) in a high frequency region and the 45° slope in the low frequency region. The absence of the semicircle in the spectrum suggests a very good ionic conductivity at the electrode/electrolyte interface.^36,37 Between the horizontal line and the 45° slope, there is a transition zone (at a resistance of 2.3 Ω), which is believed to be due to the ionic mobility in the pores of carbon, which also affects the capacitive performance of the electrode at a high current drain.²⁵ The 45° slope in the low frequency region indicates an ideal capacitive behavior of the carbon material. This further demonstrates that the carbon material can store a significant amount of electrical energy at low frequencies in the electric double layer.

Fig. 7 The Nyquist plot (a), the Bode angle plot (b) from impedance measurements of CIN-600.

The frequency response (FR) of the electrode material was depicted from the impedance measurement, and the plot is presented in Fig. 7(b). The FR reflects the number of solvated ions reaching the porous surface at a specific frequency of alternating current. It is clear from Fig. 7(b) that the imaginary part of the impedance (the capacitive part) decreases with increases in the frequency, presenting a drop in the capacitance, which is quite significant at values higher than 10 Hz. The overall map from the FR study demonstrates the better capacitive performance of the electrode materials, which may be due to the proper combination of micropores and mesopores, in which the former will favor a better efficiency of ionic access to the electrochemically active surfaces at low frequencies, while the later will facilitate ionic diffusion at high frequencies.

Conclusions

Porous carbon material was obtained by the simple carbonization of rigid co-crystal using a self-degradation template method. The carbonization was carried out at 600 °C in an argon atmosphere for 6 h in order to obtain pure carbon product. During gas adsorption and SEM analyses, it was found that the sample CIN-600 is very porous. Due to its porous nature, the sample was tested as an electrode material in EDLCs. In CV studies, the sample exhibited good voltammetric behavior, with a specific capacitance of 181.3 F g⁻¹ at 2 mV s⁻¹ and 122.3 F g⁻¹ at 150 mV s⁻¹. The good frequency response during the electrochemical impedance measurements further confirms the excellent capacitive potential of the sample. Given the broad range of acids and bases, a great variety of co-crystals with different dimensionality and porosity can be synthesized and converted into a broad range of carbon materials, which can also be structurally tuned via a judicious choice of co-formers. These preliminary results open up a new research gateway towards the synthesis of multifunctional carbon materials.

Acknowledgements

The work was financially supported by Higher Education Commission (HEC) of Pakistan (PD-IPFP/HRD/HEC/2013/1933 and 20-1638/R&D/09/2900).

Notes and references

1. M. L. Cheney, G. J. McManus, J. A. Perman, Z. Wang and M. J. Zaworotko, Cryst. Growth Des., 2007, 7, 616–617.
2. M. C. Etter, G. M. Frankenbach and J. Bernstein, Tetrahedron, 1989, 30, 3617–3620.
3. A. Chu and P. Braatz, J. Power Sources, 2002, 112, 236–246.
4. L. B. Hu, J. W. Choi, Y. Yang, S. Jeong, F. LaMantia, L. F. Cui and Y. Cui, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 21490–21494.
5. H. M. Jeong, J. W. Lee, W. H. Shin, Y. J. Choi, H. J. Shin, J. K. Kang and J. W. Choi, Nano Lett., 2011, 11, 2472–2477.
6. A. G. Pandolfo and A. F. Hollenkamp, J. Power Sources, 2006, 157, 11–27.
7. D. Pech, M. Brunet, H. Durou, P. Huang, V. Mochalin, Y. Gogotsi, P. L. Taberna and P. Simon, Nat. Nanotechnol., 2010, 5, 651–654.
8. E. Frackowiak and F. Béguin, Carbon, 2001, 39, 937–950.
9. S. R. S. Prabaharan, R. Vimala and Z. Zainal, J. Power Sources, 2006, 161, 730–736.
10. M. Arulepp, J. Leis, M. Latt, F. Miller, K. Rummaa, E. Lust and A. F. Burke, J. Power Sources, 2006, 162, 1460–1466.
11. Y. Gogotsi, A. Nikitin, H. Ye, W. Zhou, J. E. Fischer, B. Yi, H. C. Foley and M. W. Barsoum, Nat. Mater., 2003, 2, 591–594.
12. A. Jänes, T. Thomberg and E. Lust, Carbon, 2007, 45, 2717–2722.
13. J. Sutasinpromprae, S. Jitjaicham, M. Nithitanakul, C. Meechaisue and P. Supaphol, Polym. Int., 2006, 55, 825–833.
14. J. Kong, A. M. Cassell and H. Dai, Chem. Phys. Lett., 1998, 292, 567–574.
15. Y. Liang, D. Wu and R. Fu, Sci. Rep., 2013, 3, 1–5.
16. J.-K. Kim, G. Cheruvally and J.-H. Ahn, J. Solid State Electrochem., 2008, 12, 799–805.
17. T. Kyotani, L. Tsai and A. Tomita, Chem. Mater., 1996, 8, 2109–2113.
18. B. Liu, H. Shioyama, T. Akita and Q. Xu, J. Am. Chem. Soc., 2008, 130, 5390–5391.
19. S. J. Yang, T. Kim, J. HyukIm, Y. S. Kim, K. Lee, H. Jung and C. R. Park, Chem. Mater., 2012, 24, 464–470.
20. I. A. Khan, A. Badshah, N. Haider, S. Ullah, D. H. Anjum and M. A. Nadeem, J. Solid State Electrochem., 2014, 18, 1545–1555.
21. C. Journet, W. K. Maser, P. Berier, A. Loiseau, M. L. Chapelle, S. Lefrant, P. Deniard, R. Lee and J. E. Fischer, Nature, 1997, 388, 756–758.
22. A. Thess, R. Lee, P. Nikolaev, H. Dai, P. Peti, J. Robert, C. Xu, Y. H. Lee, S. G. Kim, A. G. Rinzler, D. T. Colbert, G. E. Scuseria, D. Tománek, J. E. Fischer and R. E. Smalley, Science, 1996, 273, 483–487.
23. B. Zheng, C. Lu, G. Gu, A. Makarovski, G. Finkelstein and J. Liu, Nano Lett., 2002, 2, 895–898.
24. A. Ahmadpour and D. D. Do, Carbon, 1996, 34, 471–479.
25. J. Hu, H. Wang, Q. Gao and H. Guo, Carbon, 2010, 48, 3599–3606.
26. K. S. Park, Z. Ni, A. P. Cote, J. Y. Choi, R. Huang, F. J. Uribe-Romo, H. K. Chae, M. O'Keeffe and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10186–10189.
27. D. Lozano-Castello, D. Cazorla-Amoros, A. Linares-Solano, S. Shiraishi, H. Kurihara and A. Oya, Carbon, 2004, 41, 1765–1775.
28. H. Shi, Electrochim. Acta, 1996, 41, 1633–1639.
29. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
30. L. J. Farrugia, J. Appl. Crystallogr., 1999, 32, 837–838.
31. Bruker APEX2 and SAINT Bruker AXS Inc., Madison, Wisconsin, USA 2007.
32. A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2007, 65, 148–155.
33. N. Shan, A. D. Bond and W. Jones, Cryst. Eng., 2002, 5, 9–24.
34. C. Meiners, S. E. Valiyaveettil and V. Mullen, J. Mater. Chem., 1997, 7, 2367–2374.
35. W. Sugimoto, K. Yokoshima, Y. Murakami and Y. Takasu, Electrochim. Acta, 2006, 52, 1742–1748.
36. J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Science, 2006, 313, 1760–1763.
37. R. Lin, P. Taberna, L. Chmiola, D. Guay, Y. Gogotsi and P. Simon, J. Electrochem. Soc., 2009, 156, A7–A12.
38. H. Lu, W. Dai, M. Zheng, N. Li, G. Ji and J. Cao, J. Power Sources, 2012, 209, 243–250.
39. W. Li, D. Chen, Z. Li, Y. Shi, Y. Wan, J. Huang, J. Yang, D. Zhao and Z. Jiang, Electrochem. Commun., 2007, 9, 569–573.
40. C. Ma, Y. Song, J. Shi, D. Zhang, M. Zhong, Q. Guo and L. Liu, Mater. Lett., 2012, 76, 211–214.
41. Y. S. Yun, S. Y. Cho, J. Shim, B. H. Kim, S.-J. Chang, S. J. Baek, Y. S. Huh, Y. Tak, Y. W. Park, S. Park and H.-J. Jin, Adv. Mater., 2013, 25, 1993–1998.
42. P. Guo, Y. Gu, Z. Lei, Y. Cui and X. S. Zhao, Microporous Mesoporous Mater., 2012, 156, 176–180.
43. B. Liu, H. Shioyama, H. Jiang, X. Zhang and Q. Xu, Carbon, 2010, 48, 456–463.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1002755. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4ra13482f

---