Ion kinetics in Ar/H₂ cold plasmas: the relevance of ArH⁺

Abstract

The recent discovery of ArH⁺ in the interstellar medium has aroused an interest for this ion in chemistry. In this work, the ion-molecule kinetics of cold plasmas of Ar/H₂ is investigated in glow discharges spanning the whole range of [H₂]/([H₂] + [Ar]) proportions for two pressures, 1.5 Pa and 8 Pa. Ion concentrations are determined by mass spectrometry, and electron temperatures and densities, with Langmuir probes. A kinetic model is used for the interpretation of the results. The selection of experimental conditions evinces relevant changes with plasma pressure in the ion distributions dependence with the H₂ fraction, particularly for the major ions: Ar⁺, ArH⁺ and H₃⁺. At 1.5 Pa, ArH⁺ prevails for a wide interval of H₂ fractions: 0.3 < [H₂]/([H₂] + [Ar]) < 0.7. Nevertheless, a pronounced displacement of the ArH⁺ maximum towards the lowest H₂ fractions is observed at 8 Pa, in detriment of Ar⁺, which becomes restricted to very small [H₂]/([H₂] + [Ar]) ratios, whereas H₃⁺ becomes dominant for all [H₂]/([H₂] + [Ar]) > 0.1. The analysis of the data with the kinetic model allows for the identification of the sources and sinks of the major ions over the whole range of experimental conditions sampled. Two key factors turn out to be responsible for the different ion distributions observed: the electron temperature, which determines the rate of Ar⁺ formation and thus of ArH⁺, and the equilibrium ArH⁺ + H₂ ⇄ H₃⁺ + Ar, which can be strongly dependent of the degree of vibrational excitation of H₃⁺. The results are discussed and compared with previously published data on other Ar/H₂ plasmas.

---

1. Introduction

In a recent article, Barlow et al.¹ reported the detection of the argonium ion (³⁶ArH⁺) through its 617.525 and 1234.603 GHz emission lines in spectra from the Crab Nebula recorded in the course of the Herschel mission. It is the first noble gas compound observed hitherto in space. Barlow et al.¹ suggested that ArH⁺ is formed most likely in transition zones between fully ionized and molecular gas and that electron collisions provide the likely excitation mechanism. Shortly afterwards, Schilke et al.² assigned a previously unidentified absorption at 617.5 GHz to ³⁶ArH⁺ in the diffuse interstellar medium (ISM), present in spectral line surveys toward many galactic sources. The two astronomically relevant ³⁶ArH⁺ and ³⁸ArH⁺ isotopologues of argonium were found in these surveys. From a careful analysis of the observations using a chemical model for diffuse molecular clouds, the authors concluded that ArH⁺ should be a very good tracer of gas with very low (10⁻⁴ to 10⁻³) fractional abundances of H₂. The fresh discovery of ArH⁺ in different chemical environments in the ISM has revived the interest in the mechanisms for the production and destruction of this ion.

In the laboratory, ArH⁺ is usually produced in electrical discharges containing Ar and H₂. The properties of different types of Ar/H₂ discharges have been experimentally investigated and theoretically modeled by a number of research groups^3–17 due largely to their interest for many technical applications like elemental analysis,^18–21 sputtering,^22–25 film deposition,^26,27 hydrogenation,^28,29 or functionalization of nanostructured materials.^30,31 Questions addressed in these studies include the loss of global ionization upon addition of H₂ to an Ar plasma, the modification of the electron energy distributions, the role of metastable Ar atoms and that of the excited states of H₂, the reforming of precursors,³¹ or the distinct effects of physical and chemical sputtering on the characteristics of substrate films (see for instance discussions in ref. 5, 10, 24 and 29). An illustrative example of the relevance of ArH⁺ in a technological process can be found in the work of Budtz-Jørgensen et al.,²³ who found that highly energetic ArH⁺ ions were responsible for most of the physical sputtering of gold surfaces in Ar/H₂ direct current (dc) discharges. In these plasmas, the primary Ar⁺ ions lose much of their energy, and thus of their sputtering efficiency through symmetric charge exchange collisions with Ar atoms in the sheath before reaching the gold surface.

The ion chemistry in Ar/H₂ plasmas was also specifically considered, with varying degree of detail, in some of the works cited in the previous paragraph. Bogaerts and co-workers developed theoretical models for different types of glow discharges.^10–12 In their hybrid Monte Carlo fluid model for dc discharges,¹⁰ Bogaerts and Gijbels simulated the conditions of a typical glow discharge used for analytic mass spectrometry (1% H₂ in Ar, 70 Pa). The model calculations yielded an ionic distribution dominated by Ar⁺, with ArH⁺ and H₃⁺ also having a significant presence, along with very small amounts of H⁺ and H₂⁺. Qualitatively similar ion distributions were also obtained in the modeling of a higher pressure (850 Pa) Grimm type dc discharge¹¹ and of a capacitively coupled radio frequency (rf) discharge¹² operating at lower pressures (7 to 33 Pa). The results of these models were of great help for the identification of key processes in the discharges, but could not be directly compared to experimental measurements.

Distributions of ion densities in inductively coupled rf discharges were also modeled, but not measured, in the recent works of Kimura and Kasugai¹³ and Hjartarson et al.¹⁴ They used self-consistent global models to study Ar/H₂ discharges with variable mixture proportions in the pressure ranges 2.7 to 8 Pa and 0.13 to 13 Pa, respectively. In both works, the major ions were Ar⁺, H₃⁺ and ArH⁺, with different relative concentrations depending on the pressure and mixture conditions, but in no case was ArH⁺ the prevalent ion.

A detailed comparison of experimental ion distributions and model calculations for Ar/H₂ inductively coupled rf plasmas for a total pressure of 1 Pa was recently reported by Sode et al.^16,17 In contrast with the calculations of ref. 13 and 14, the measurements of Sode et al. revealed that ArH⁺ was the dominant ion over much of the Ar fraction range investigated, where it accounted for roughly two thirds of the positive charge. Their model reproduced the overall trends in the evolution of the ion distributions, but underestimated the measured ArH⁺ concentration and overestimated the H_x⁺ densities. Sode et al.¹⁷ noted that their measurements and calculations would be in much better agreement by assuming a zero rate coefficient for the ArH⁺ + H₂ → H₃⁺ + Ar reaction, instead of the large literature values currently used, which are in the upper half of the 10⁻¹⁰ cm³ s⁻¹ range (see ref. 32 and the references therein).

A comparison of experimental and calculated ion density distributions in Ar/H₂ plasmas was also reported in a previous work by our group¹⁵ for a dc hollow cathode discharge. The experiments were carried out at pressures of 0.7 and 2 Pa for a [H₂]/([H₂] + [Ar]) ratio of 0.85. For this small Ar fraction, the discharges were dominated by hydrogen ions (H₃⁺ at 2 Pa and H₃⁺ and H₂⁺ for 0.7 Pa), but ArH⁺ ions were second in abundance. The experiments also showed the presence of a small amount of Ar²⁺ ions. The measured ion distributions could be well accounted for by a kinetic model if a tiny fraction of high energy electrons (>50 eV) was used in the calculations. Hollow cathodes and other types of dc glow discharges were used for spectroscopic studies of the ArH⁺ ion.^33–39 In these works, the absolute concentration of ArH⁺ in the discharge was empirically maximized, and it was found that the largest ArH⁺ signals were obtained with a small H₂ fraction,^34–38 or even with no H₂ at all^33,39 in the precursor mixture. This seeming paradox suggests that hydrogen from small impurities or from the reactor walls would be adequate to produce significant amounts of ArH⁺ in the plasma. In general, these discharges were run at higher pressures (>30 Pa) than those discussed in the previous paragraphs.

The present work intends to shed light on the details of the ionic chemistry in Ar/H₂ plasmas and, in particular, of the processes leading to the production and destruction of ArH⁺ for different plasma conditions. To this aim, we have used an approach combining a thorough experimental diagnosis of the plasmas (including the measurements of electron temperatures and densities, as well as the distributions of stable neutrals and ions) with a simple kinetic model of the ion chemistry. We have investigated hollow cathode discharges, spanning the whole range of [H₂]/([H₂] + [Ar]) mixture proportions for two different pressures, 1.5 Pa and 8 Pa. The relative densities of the various ions have been found to vary markedly between these pressures over the range of mixture proportions sampled. The kinetic model provides a clear picture of the chemistry underlying the observed ion distributions and has helped identify the main sources and sinks of the major plasma ions (Ar⁺, ArH⁺ and H₃⁺). The results are discussed and whenever possible compared to previous works.

2. Experimental

The experimental set-up for the present studies has been described in previous works.^15,40–42 It consists of a grounded cylindrical stainless steel vessel (10 cm diameter, 34 cm length) that constitutes the cathode, and a central anode. The chamber can be pumped to a background pressure of 10⁻⁴ Pa with a 300 l s⁻¹ turbomolecular pump, backed by a dry mechanical pump. The chamber walls have different ports for connection of gas inlets, diagnostics tools, observation windows, and pressure gauges. The chamber pressure was controlled by balancing the flow of the precursor gases with needle valves at the entrance and a butterfly valve at the exit of the reactor. The position of the butterfly valve was kept fixed during the experiments. Two discharge pressures 1.5 Pa and 8 Pa were investigated. For each pressure, the whole range of H₂ fractions was sampled. The plasma current was kept fixed at a value of 150 mA for all the experiments. The supply voltages were in the 300 to 400 V range, which correspond to discharge powers of 45 to 60 W. An electron gun with a tungsten wire operating at 2 A and −2000 V_dc was used to initiate the discharge, and was then switched off.

A plasma monitor (PM), based in a quadrupole mass spectrometer, with ion energy resolution, was employed to detect the plasma ions. The PM was installed in a differentially pumped chamber connected to the reactor through a 100 µm diaphragm. During operation, the pressure in the detection chamber was kept in the 10⁻⁵ Pa range by a 150 l s⁻¹ turbomolecular pump backed by a dry pump. The same chamber contained a quadrupole mass spectrometer that was used to monitor the composition of the discharge precursor mixture in the reactor vessel.

Ion fluxes were calculated by integrating the ion energy distributions recorded by the PM for each individual ion. For the discharge pressures used in our experiments, the ion energy distributions measured at the cathode were in general narrow, with a peak close to the value of the cathode–anode potential, which indicates that for the comparatively large energies of the ions reaching the cathode, the plasma sheath is only mildly collisional for most species, i.e., the number of effective collisions is low and should not distort appreciably the ion fluxes between plasma and cathode. Appreciable effects of sheath collisions are only found for ions susceptible to undergo symmetric charge exchange with the dominant neutrals (Ar⁺ and H₂⁺). This process, characterized by large cross-sections, leads to the appearance of a low-energy tail that grows at the expense of the narrow peak with increasing pressure,⁴³ but should not lead to a significant reduction of the measured flux for these ions. For our typical sheath potentials (up to a few hundred eV), asymmetric charge exchange between Ar⁺ and H₂ could also take place¹⁵ to a lesser extent, but for the present overall results, this process should only play a minor role. The sensitivity of the PM to the masses of different ions was calibrated with the noble gases He, Ne, and Ar. To this aim, the PM was used in the neutral detection mode (i.e. with the electron bombardment ionizer) and the signals of He, Ne and Ar were compared to the corrected readings of a Bayard-Alpert gauge located in the same chamber. This calibrated sensitivity corresponds to the whole ion detection system (energy analyzer, mass filter and multiplier). Most measurements were performed with a multiplier voltage of 3200 V and the relative detection sensitivity for a given singly charged ion of mass, m_i, was found to be proportional to ∼m_i^−0.22. Some of the experiments carried out with this multiplier voltage led to signal saturation (more than 2 × 10⁶ counts s⁻¹) and it was necessary to perform the measurements with a multiplier voltage of 2800 V. In this case, the relative ion-mass sensitivity was ∼m_i^−0.71. The density of a given ion in the plasma glow was derived by multiplying the measured ion flux at the cathode by a factor (m_i/q_i)^0.5 to correct for the dependence of the flow velocity on the ion mass. We have not considered a dependence of the PM sensitivity on the incoming ion energy, assuming that it is a small source of error, since our energy distributions are predominantly narrow.

Electron mean temperatures, T_e, and densities, N_e, were measured with a double Langmuir probe built in our laboratory, under the assumptions of collision free probe sheath and orbital limited motion.⁴⁴ To estimate total charge densities from the characteristic curves of the Langmuir probe, a mean ion mass was used in each case, weighted according to the ion density distributions deduced from the PM measurements. Note that the derivation of T_e from the double Langmuir probe measurements implies the assumption of a Maxwellian electron energy distribution function.⁴⁵

3. Kinetic model

For the analysis of the experimental measurements, we have used a simple zero-order kinetic model developed in our group, which is briefly described here. More detailed accounts can be found in ref. 15 and 41. The model is based on the numerical integration of a set of coupled differential equations accounting for the time evolution of the various chemical species from the discharge ignition to the attainment of the steady state. It uses the experimental partial pressures and flows of the precursor gases as input parameters and also the electronic temperatures, T_e, and densities, N_e, which are assumed to be homogeneous throughout the plasma (negative glow) volume. It is further assumed that the ion temperature in the glow, T_ion, is similar to the gas temperature (T_ion ≈ 300 to 400 K), analogous to what was found in previous spectroscopic studies of dc hollow cathode discharges.^39,46 The concentration of the various plasma species is assumed to be controlled by the set of homogeneous and heterogeneous reactions listed in the first column of Table 1 and 2. General comments on these processes can be found in our previous work,¹⁵ where basically the same set of reactions was employed (see below). Rate coefficients for collision processes with Maxwellian electrons are listed in the second column of Table 1 with an indication of their sources. In general, these values have been derived from cross section data using the expression k = 〈σv〉, with σ being the cross section for the process of interest and v the relative velocity of the colliding partners.

Table 1 Homogeneous reactions and rate coefficients, k (cm³s⁻¹). k^A: rate coefficients for Maxwellian electrons at T_e (eV). k^B: rate coefficients for high energy electrons (>50 eV, see text). Two alternative values are given for the rate coefficient of reaction (18): ^Hk₁₈ and ^Lk₁₈. The origin of these coefficients and their influence in the model simulations is discussed in the text.

Homogeneous reactions	k ^A	k ^B
a a = 7.51 × 10^−9, b = −1.12 × 10^−9, c = 1.03 × 10^−10, d = −4.15 × 10^−12, e = 5.86 × 10^−14. b K = 8.39 × 10^−9 + 3.02 × 10^−9 × Te – 3.80 × 10^−10 × Te^2 + 1.31 × 10^−11 × Te^3 + 2.42 × 10^−13 × Te^4 − 2.30 × 10^−14 × Te^5 + 3.55 × 10^−16 × Te^6.
(1) H + e → H^+ + 2e	6.50 × 10^−9 × Te^0.49 × e^−12.89/Te (ref. 41)	4.2 × 10^−8 (ref. 15)
(2) H2 + e → H^+ + H + 2e	3.00 × 10^−8 × Te^0.44 × e^−37.73/Te (ref. 41)	4.5 × 10^−9 (ref. 15)
(3) H2^+ + e → H^+ + H + e	1.07 × 10^−7 × Te^0.049 × e^−9.69/Te (ref. 41)
(4) H2^+ + e → H^+ + H^+ + 2e	2.12 × 10^−9 × Te^0.31 × e^−23.30/Te (ref. 41)
(5) H2^+ + H → H2 + H^+	6.4 × 10^−10 (ref. 32)
(6) H2 + H^+ → H2^+ + H	1.19 × 10^−22 (ref. 41)
(7) H2 + e → H2^+ + 2e	3.12 × 10^−8 × Te^0.17 × e^−20.08/Te (ref. 41)	5.0 × 10^−8 (ref. 15)
(8) H3^+ + e → H2^+ + H + e	4.85 × 10^−7 × Te ^−0.05 × e^−19.17/Te (ref. 41)
(9) H2^+ + e → H* + H	a + b × Te + c × Te^2 + d × Te^3 + e × Te^4^a (ref. 41)
(10) H2^+ + H2 → H3^+ + H	2.0 × 10^−9 (ref. 32)
(11) H3^+ + e → 3H	0.5 × K^b (ref. 41)
(12) H3^+ + e → H2 + H	0.5 × K^b (ref. 41)
(13) H2 + e → 2H + e	1.75 × 10^−7 × Te^−1.24 × e^−12.59/Te (ref. 41)	1 × 10^−8 (ref. 15)
(14) Ar + e → Ar^+ + 2e	2.53 × 10^−8 × Te^0.5 × e^−16.3/Te (ref. 15)	1.6 × 10^−7 (ref. 15)
(15) Ar + e → Ar^2+ + 3e	2.58 × 10^−9 × Te^0.5 × e^−47/Te (ref. 15)	1.1 × 10^−8 (ref. 15)
(16) Ar^+ + e → Ar^2+ + 2 e	1.9 × 10^−8 × Te^0.5 × e^−27.7/Te (ref. 15)
(17) H2^+ + Ar → ArH^+ + H	2.1 × 10^−9 (ref. 32)
(18) H3^+ + Ar → ArH^+ + H2	^H k 18 = 3.65 × 10^−10 (ref. 32)
	^L k 18 = 1 × 10^−11 (ref. 47)
(19) Ar^+ + H2 → H2^+ + Ar	0.02 × 8.9 × 10^−10 (ref. 32)
(20) Ar^+ + H2 → ArH^+ + H	0.98 × 8.9 × 10^−10 (ref. 32)
(21) ArH^+ + H2 → H3^+ + Ar	6.3 × 10^−10 (ref. 32)
(22) Ar + e → Ar* + e	9.90 × 10^−10 × Te^−0.08 × e^−11.72/Te (ref. 14)	2.4 × 10^−8 (ref. 10)
(23) Ar* + H2 → 2H + Ar	7.0 × 10^−11 (ref. 10)
(24) Ar* + Ar* → Ar + Ar^+ + e	6.4 × 10^−10 (ref. 10)

---

Table 2 Heterogeneous processes

Heterogeneous reactions	Wall reaction coefficients
(1) H + wall → H2	γ = 0.03
(2) H^+ + wall → H	γ = 1
(3) H2^+ + wall → H2	γ = 1
(4) H3^+ + wall → H2 + H	γ = 1
(5) Ar^+ + wall → Ar	γ = 1
(6) ArH^+ + wall → Ar + H	γ = 1
(7) Ar^2+ + wall → Ar	γ = 1
(8) Ar* + wall → Ar	γ = 1

---

Arrhenius-like functions or polynomials are used to express the dependence of these rate coefficients on T_e. Rate coefficients for ion-molecule reactions, also listed in the first column of Table 1, have been mostly obtained from the compilation of Anicich.³² For reaction (18) (H₃⁺ + Ar), an alternatively much smaller rate constant from the tables of Albritton⁴⁷ has also been considered. The meaning of the two values is discussed at length in the next section. Throughout the text, reactions are referred to using the numbers of this table. It is well known that in hollow cathode discharges, there is a high energy component in the electron energy distribution that results from secondary electron emission by the cathode, which is responsible for the presence of Ar²⁺ ions in our plasmas. In the third column of Table 1 we have included a series of rate coefficients for high energy electrons (∼50 to 300 eV) derived also from cross section data (see ref. 15 for details). The amount of high energy electrons within this energy range is very small. Specifically, for the present study we have used fractions of 3 × 10⁻⁴ and 3 × 10⁻⁶ high energy electrons for the 1.5 Pa and 8 Pa discharges, respectively, that are enough to justify the observed Ar²⁺ density. These minute amounts of high energy electrons are unrelated to the Maxwellian electron energy distributions underlying the Langmuir probe measurements. In any case, with the densities assumed here, these high energy electrons would be undetectable by the probes and play no appreciable role in the global kinetics.

Metastable argon atoms (Ar*) in 4s³P₂ and 4s³P₀ states, formed by electron impact, were not included in our previous work⁴¹ but have been incorporated here, as they can contribute to the formation of atomic hydrogen through the reaction Ar* + H₂ → Ar + H + H (reaction (23)). They can also lead to the formation of Ar⁺ through Penning ionization (reaction (24)). Ar* de-excitation at the wall is also included (see Table 1 and 2). The calculations show that the highest concentrations of Ar* are similar to the electron densities, and that their influence in the global chemistry of the discharge is very small: H densities increase just by 4% at most and the changes in the other species are negligible.

Negative ions and excited states of H₂ are not contemplated in the kinetic model. Negative H⁻ ions can be formed in hydrogen plasmas and, in fact, there is a great interest in the development of sources of H⁻ based on different kinds of hydrogen discharges.^48,49 However, the production of this ion, usually through dissociative electron attachment to H₂ molecules, requires molecules in highly excited vibrational levels (especially v ≥ 4).⁵⁰ In our previous study of emission spectroscopy of pure H₂ in conjunction with a collisional radiative model,⁴¹ it was shown that the H₂ vibrational populations in our plasmas are concentrated in the lowest levels and can be roughly described by a vibrational temperature of ∼3000 K. The population of H₂(v ≥ 1) is ∼12% and that of H₂(v = 4) is only ∼0.05%. Under these conditions, we do not expect the dissociative attachment channel to be relevant. Estimates based on model calculations and photodetachment measurements⁵⁰ indicate that the concentration of H⁻ in a hollow cathode discharge of hydrogen and neon is orders of magnitude lower than that of electrons. Consequently, we have assumed that electrons are the only negative charge carriers in our plasmas. Likewise, given the high threshold for electron impact dissociation of H₂ (∼11 eV) as compared with the first vibrational quantum of H₂ (∼0.5 eV), we do not expect a significant contribution of vibrationally excited molecules, H₂(v), to the global electron impact dissociation of H₂. The decrease in population with growing v is far more important than the increase in the rate coefficient due to the lower energy threshold. Recent model simulations of rf discharges have variously considered H⁻ and H₂(v). Hjartarson et al.¹⁴ included both vibrational excitation and negative ions in their calculations. In contrast, Sode et al.¹⁷ did not include them and obtained a reasonable agreement between their results and those of Hjartarson et al.¹⁴ regarding the ion chemistry. Sode et al.¹⁷ concluded that H⁻ and H₂(v) are not crucial for the description of the positive ion densities, which is the subject of the present work.

The heterogeneous processes considered in the model are reduced to wall recombination of H atoms to form H₂, and wall neutralization of the various positive ions (see Table 2). In analogy with ref. 15 and 41 the recombination of hydrogen atoms is accounted for with a single γ coefficient. A more refined treatment of H atom recombination at the wall, including adsorption and reaction steps, was introduced in a previous work by our group⁵¹ to describe H/D isotope exchange at the reactor walls. In the present study, with no isotope exchange and focusing on the ionic chemistry in the gas phase, we have kept the simplified original model for the H₂ wall recycling. Atomic hydrogen concentrations are outside the scope of this work and were not measured. However, for the sake of completeness they have been estimated with the model. The major source of H atoms is the electron impact dissociation of H₂ (reaction (13)). This is also the main mechanism for the production of H atoms in the rf plasma models mentioned above.^13,14,17 The relative H concentrations, [H]/([H] + [H₂] + [Ar]), are always below 8% of the total concentration of neutral particles for all the conditions considered. In any case, H atoms have very little influence on the ionic chemistry, which is always dominated by collisions of ions with the major neutral species, Ar and H₂.

4. Results and discussion

4.1 Electron temperatures and densities

The measured electron temperatures and densities are shown in Fig. 1 for the two pressures investigated, as well as the values used for the modeling (see below). For the 1.5 Pa discharge, the electron density shows a slow monotonic decline that becomes more pronounced for [H₂]/([H₂] + [Ar]) > 0.8. In the 8 Pa discharge, there is an abrupt drop in electron density for [H₂]/([H₂] + [Ar]) < 0.1. For larger ratios, N_e hardly decreases with growing H₂ content. In our experiments, where the discharge current is kept fixed in all cases, the evolution of the electron density, which equals the ion density due to the electroneutrality condition, is determined to a large extent by the ion composition in the plasma (see below). The flow of the heavier ions (Ar⁺, ArH⁺) to the cathode is much slower than that of the hydrogen species (mostly H₃⁺). Consequently, in plasmas where heavy ions are predominant, a higher ion density is needed to maintain the same current as in plasmas dominated by light ions. Therefore, the total ion (and electron) density decreases with growing H₂ content. A qualitatively similar decrease was observed in the experiments with inductively coupled Ar/H₂ plasmas.^6,13,14,16

Fig. 1 Evolution of the electron temperature (upper panels) and density (lower panels) as a function of the H₂ fraction for the 1.5 Pa (left) and the 8 Pa (right) discharge. Solid symbols: experimental values. Lines: values used in the kinetic model.

The measured electron temperatures are higher, as expected, for the lower pressure (1.5 Pa) discharge. For this pressure, within the experimental uncertainties, the T_e values oscillate around a constant value of ≈2.8 eV, regardless of the mixture proportion. This temperature is consistent with those of previous experiments by our group for [H₂]/([H₂] + [Ar]) = 0.85 hollow cathode discharges in a similar pressure range.¹⁵ For the 8 Pa discharge, T_e reaches a maximum value of 2.6 eV for H₂ fractions of ∼0.1, but it lies between 2.2 and 1.7 eV over most of the relative concentration interval. Similar or somewhat higher electron temperatures are found for inductively coupled discharges at comparable pressures.^13,14,17 In those rf plasmas, however, the electron temperature shows a smooth variation over a wide range of mixture proportions, but tends to increase appreciably for the highest H₂ fractions. This tendency is not observed in the Langmuir probe measurements for our hollow cathode discharges, which give similar values for the pure H₂ and pure Ar plasmas within experimental uncertainty. At present we have no explanation for this contrasting behavior.

4.2 Ion distributions

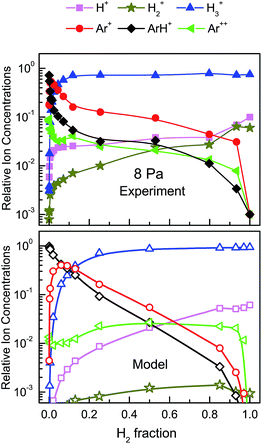
The relative ion concentrations determined in the experiments are displayed in Fig. 2–5, together with model simulations. The absolute concentrations for a given ion can be readily derived by multiplying its relative concentration by the total ion density, which coincides with the electron density for the same pressure and mixture proportion (see Fig. 1). Fig. 2 and 3 represent the relative ion concentrations for 1.5 Pa and 8 Pa in linear scale. The experimental values are shown in the middle panels. Note that for the two pressures and for all H₂ fractions, the distributions are dominated by Ar⁺, ArH⁺ and H₃⁺ but important changes can be observed between both panels: (1) a very marked displacement of the ArH⁺ maximum towards the lowest H₂ fraction at the highest pressure, (2) a drastic reduction of the Ar⁺ prevalence region and (3) a noticeable broadening of the H₃⁺ dominance region. For a better understanding of these results, four model simulations have been carried out, two for each of the two discharge pressures studied. For each pressure, their respective T_e and N_e set of values have been used (see Fig. 1), and the only difference between the two simulations is the rate coefficient for the reaction of H₃⁺ with Ar (reaction (18)), which may be strongly dependent on the internal excitation of the H₃⁺ ion, as we shall discuss below. The recommended value from the compilation of Anicich³² (3.65 × 10⁻¹⁰ cm³ s⁻¹) is taken as the higher k₁₈ (termed ^Hk₁₈ hereinafter) for the calculations. The corresponding results are displayed in the lower panels of Fig. 2 and 3. As a lower value for k₁₈, we have taken the rate coefficient from the tables of Albritton⁴⁷ (1 × 10⁻¹¹ cm³ s⁻¹, termed ^Lk₁₈ hereinafter) (see upper panels of Fig. 2 and 3). Fig. 4 and 5 represent the ion distributions for the two pressures using a logarithmic ordinate scale for a better appreciation of the minor ions: Ar²⁺, H⁺ and H₂⁺.

Fig. 2 Relative ion distributions as a function of the H₂ fraction for the 1.5 Pa discharge. Middle panel: Experimental measurements. Lower panel: Model simulation with ^Hk₁₈. Upper panel: Model simulations with ^Lk₁₈ (see text).

Fig. 3 Same as Fig. 2, but for the 8 Pa discharge.

Fig. 4 Relative ion distributions for the 1.5 Pa discharge. Upper panel: experimental measurements. Lower panel: model simulation with ^Hk₁₈ = 3.65 × 10⁻¹⁰ cm³ s⁻¹ and fraction of high energy (>50 eV) electrons of 3 × 10⁻⁴ (see text).

Fig. 5 Relative ion distributions for the 8 Pa discharge. Upper panel: experimental measurements. Lower panel: model simulations with ^Lk₁₈ = 1 × 10⁻¹¹ cm³ s⁻¹ and a fraction of high energy electrons of 3 × 10⁻⁶.

For the two pressures, the experimental Ar⁺ density decreases monotonically with growing H₂ proportion, but the decrease is slower in the 1.5 Pa discharge (middle panel of Fig. 2). In this plasma, ArH⁺ is the second ion in abundance for H₂ fractions between 0.05 and 0.3 and becomes the major ion for ratios between 0.3 and 0.7. The relative concentration of H₃⁺ grows monotonically with increasing H₂ content, surpasses that of Ar⁺ for H₂ fractions ∼0.4, and becomes dominant for fractions larger than 0.7. In the 8 Pa discharge (middle panel of Fig. 3), the ion distribution is dominated by H₃⁺ for most of the mixture ratios, ArH⁺ prevails over a very narrow interval (0.005 to 0.03) of H₂ fractions, and Ar⁺ is the major ion only when there is virtually no H₂ in the discharge.

For the 1.5 Pa discharge, the best agreement between measurements and simulations is obtained with ^Hk₁₈ = 3.65 × 10⁻¹⁰ cm³ s⁻¹.³² With this rate constant, the model provides a good global description of the measured ion distributions. It accounts for the decrease of Ar⁺ with increasing H₂ fraction, for the dominance of ArH⁺ at intermediate H₂ fractions, where this ion concentrates 40% of the positive charge, and for the final prevalence of H₃⁺ in the mixtures with the highest H₂ content. The calculations render well the crossing between the Ar⁺ and the H₃⁺ curves, although the predicted interval of ArH⁺ prevalence is shifted slightly toward lower H₂ fractions. The model results with ^Lk₁₈ = 1 × 10⁻¹¹ cm³ s⁻¹,⁴⁷ are shown in the upper panel of Fig. 2. The agreement between measurements and calculations is now worse: the predicted ArH⁺ is never clearly dominant and the crossing between the decreasing ArH⁺ and the growing H₃⁺ takes place at a lower H₂ fraction.

For the 8 Pa discharge, the application of the model with ^Hk₁₈ leads to the ion distributions depicted in the lower panel of Fig. 3. The agreement with experiment is much worse here than in the previous case. The model indeed predicts a steeper decrease of the Ar⁺ concentration than that of the 1.5 Pa discharge and a shifting of the ArH⁺ maximum toward a lower H₂ fraction, but this maximum is too broad and the descent of the ArH⁺ density too slow. The rise of the H₃⁺ concentration is likewise too gradual as compared with the experimental data. The accordance between experiment and model improves significantly if ^Lk₁₈ is employed in the calculations. In this case, H₃⁺ dominates largely the ion distributions over most of the H₂ fraction range, and ArH⁺ exhibits a comparatively narrow maximum for a low (<0.1) H₂ fraction. In spite of the described improvement, the variation in the main ion concentrations predicted by the model is still too gentle in comparison with the measurements.

The distribution of the minor ions in the two discharges can be better seen in the logarithmic representations of Fig. 4 and 5. In this case, for the sake of clarity, model simulations are restricted to those giving a better agreement with the measurements (i.e. with ^Hk₁₈ for 1.5 Pa and ^Lk₁₈ for 8 Pa). Overall, a better agreement is obtained for the 1.5 Pa discharge. The model predicts the expected increase in the relative weight of the minor hydrogen ions, H⁺ and H₂⁺, with growing H₂ proportion, although the concentration of H₂⁺ is underestimated by up to an order of magnitude. Finally, as discussed above, the small amount of Ar²⁺ observed in the measurements can be justified by assuming a very small fraction (<5 × 10⁻⁴) of electrons with energies higher than 50 eV that would be undetectable by the Langmuir probes.

4.3 Key reaction mechanisms

The analysis of the results shows that just two key factors are responsible for the main differences between the distributions of the major plasma ions at the two discharge pressures studied: the electron temperature and the k₁₈ value, which is closely related with the degree of vibrational excitation of H₃⁺. The effect of T_e can be appreciated in Fig. 6. For any T_e value, the rate for electron impact ionization of Ar (k₁₄) is 6 to 7 times larger than that for H₂ (k₇), consequently, among the primary ions, Ar⁺ will prevail over H₂⁺ up to very high fractions of hydrogen. A drop in electron temperature, from 3 to 2 eV, similar to that observed upon increasing the discharge pressure from 1.5 to 8 Pa, results in an approximate 30-fold decrease of k₁₄ and k₇ and, thus, in a much larger relative weight of ion-molecule chemistry vs. electron impact ionization. This explains the steep descent in the Ar⁺ density with growing H₂ ratio observed in the 8 Pa discharge. The primary Ar⁺ ions generated by electron impact (reaction (14)) are immediately transformed into ArH⁺ through reaction (20), with a rate coefficient (k₂₀) that is nearly 100 times larger than k₁₄ at 2 eV. In the case of the 1.5 Pa discharge, the ratio between these two coefficients is roughly a factor of four, which leads to a more gradual evolution of the concentrations of Ar⁺ and ArH⁺. With a further increase in the proportion of H₂, collisions of ArH⁺ with hydrogen molecules (reaction (21)) gain in importance and lead to the production of H₃⁺. Part of these H₃⁺ ions can revert to ArH⁺ through reaction (18). Reactions (17) and (10) can also contribute to the production of ArH⁺ and H₃⁺ respectively but, given the small density of H₂⁺ ions in the plasmas considered, they play only a minor role.

Fig. 6 Rate coefficients for the most relevant electron impact and ion-molecule reactions in the Ar/H₂ discharges as a function of electron temperature. The two values of k₁₈ used in the model simulations are shown.

The importance of internal energy effects in the equilibrium between the reactions (18) and (21), interconverting ArH⁺ and H₃⁺, has been addressed in previous works.^52–56 Reaction (21) leading from ArH⁺ to H₃⁺ is exothermic by about 0.55 eV.⁵⁵ Rate coefficient measurements for this reaction performed by various groups yield mostly large values ≈(5 to 15) × 10⁻¹⁰ cm³ s⁻¹, as expected for an exothermic ion-molecule reaction (see references in ref. 32). The rate constant recommended by Anicich³² (k₂₁ = 6.3 × 10⁻¹⁰ cm³ s⁻¹) and used in the present model is thus a reasonable choice. The reverse reaction (18), leading from H₃⁺ to ArH⁺ is endothermic by 0.55 eV. In this case, the recommended value,³² k₁₈ = 3.65 × 10⁻¹⁰ cm³ s⁻¹ (^Hk₁₈), corresponds to the ion-cyclotron resonance (ICR) measurements of Bowers and Elleman⁵⁷ and is about 60% of the recommended value for reaction (21), but later measurements by Roche et al.⁵⁸ indicated that k₁₈ should be at most an order of magnitude smaller than k₂₁. Taking this experiment into account, Albritton⁴⁷ gave an upper limit of k₁₈ = 1 × 10⁻¹¹ cm³ s⁻¹ (^Lk₁₈).

We attribute the large discrepancy between the k₁₈ values estimated by the two groups to the different experimental methods used. In the experiments of Bowers and Elleman⁵⁷ the source of H₃⁺ is the reaction of H₂⁺ ions with H₂ molecules (reaction (10)). As noted by the authors, the high exoergicity of this reaction⁵⁹ (1.72 eV) could be largely stored as vibrational energy of the nascent H₃⁺, which would not be significantly deactivated by collisions in the low pressure ICR measurements. The large rate coefficient determined in this experiment would thus pertain to the reaction of [H₃⁺]* + Ar, which becomes exothermic for an internal excitation energy higher than 0.55 eV. In contrast, the measurements of Roche et al.,⁵⁸ setting a much smaller upper limit for k₁₈, were performed in a flow reactor with a much more efficient collisional relaxation of the H₃⁺ reactant, and corresponds most probably to an endothermic H₃⁺ + Ar reaction.

Experimental and theoretical works^{52,53,60–62} indicate that the H₃⁺ ions produced in reaction (10), which is favored in plasmas with a very large hydrogen fraction, are highly vibrationally excited and that this excitation can be effectively quenched through collisions with H₂, but there is no unanimity on the actual relaxation efficiency. In plasmas with Ar and H₂, reaction (21) can become the main source of H₃⁺. If the reaction takes place with ground state ArH⁺, the resulting H₃⁺ ions will not have enough vibrational excitation to revert the process through reaction (18) and will remain as H₃⁺. However, if ArH⁺ is vibrationally excited, it can transfer part of its excitation to the H₃⁺ product, which could then react back with Ar displacing the equilibrium of reactions (18) and (21) toward the reconstruction of ArH⁺.⁵⁶ The main source of ArH⁺ in Ar containing plasmas is the reaction of Ar⁺ with H₂ (reaction (20)). These reactions have been studied, both experimentally and theoretically (see for instance ref. 63 and 64 and references therein), but still many aspects of its state specific dynamics and, in particular, of the energy partitioning among the nascent product molecules are not known with precision. Trajectory calculations by Chapman⁶⁵ on a semiempirical potential energy surface indicate that a large fraction of the exothermicity of reactions (17) and (20) should appear initially as vibrational excitation of ArH⁺. In the presence of sufficient Ar, the internal excitation of ArH⁺ could be quenched through the process:⁵⁴ (ArH⁺)* + Ar → ArH⁺ + Ar*. Electron impact could also provide a mechanism for the vibrational excitation of H₃⁺ in plasmas.⁶⁶

To summarize, although the degree of vibrational excitation of the nascent ArH⁺ and H₃⁺ and the relevance of the likely relaxation pathways is not precisely known, it is reasonable to expect that collisional relaxation and, in particular, that of the sensitive H₃⁺ ion, will be appreciably higher in the 8 Pa experiments than in those at 1.5 Pa. To simulate this effect in a simple manner, we have taken the rate coefficient of Albritton (^Lk₁₈ = 1 × 10⁻¹¹ cm³ s⁻¹) for the endothermic process with vibrationally relaxed H₃⁺. Comparison of the upper and lower panels of Fig. 2 and 3 shows that the influence of introducing ^Lk₁₈ in the kinetic model is much more marked in the ion distributions of the 8 Pa discharge, which are now in reasonable accordance with experiment. Further tests with the kinetic model show that a much better agreement is obtained with a lower electron temperature (1.7 to 1.8 eV) for the lower H₂ fractions. Nevertheless, for consistency, we present only the simulations corresponding to electron temperatures within the estimated uncertainty of the probe measurements. We note however that the double Langmuir probes used in our measurements provide only an estimate of T_e under the assumption of Maxwellian electron energy distributions and are not sensitive to the actual shape of the high energy tail of the distribution. A selective depletion of electrons in this high energy tail would go unnoticed in the probe measurements, but would correspond to an effective lower electron temperature for the kinetics.

The increase in the discharge pressure has thus, a two-fold effect on the concentration of ArH⁺. On one hand, it lowers the electron temperature decreasing the rate of formation of Ar⁺, the main ArH⁺ precursor. On the other hand, it can lead to the quenching of the internal excitation of H₃⁺, diminishing markedly the rate of reaction (18), which is also a source of ArH⁺. As a consequence, the prevalence of ArH⁺ is restricted to a very narrow range of mixture proportions with very little H₂. This behavior explains also the puzzling results of the many spectroscopy experiments mentioned above,^33–39 where the best ArH⁺ signals were found with little or no H₂ at all in the precursor gas. The conditions in these experiments, usually performed with comparatively high discharge pressures, are qualitatively similar to the present results for the 8 Pa discharge, where the optimal condition for ArH⁺ is obtained with just traces (less than 3%) of H₂. Furthermore, we have observed by mass spectrometry in a different hollow cathode discharge cell,³⁹ using 40 Pa of pure Ar as precursor that a tiny amount (∼0.2 Pa) of H₂ is ejected from the cathode when the discharge is on. This small amount of H₂ provided an adequate concentration of ArH⁺ for spectroscopic measurements.

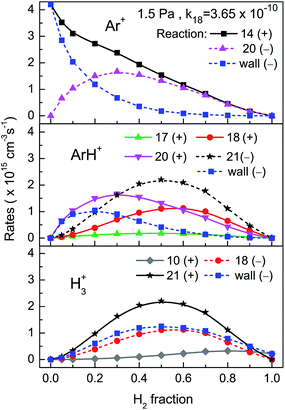
4.4 Main formation and loss rates

The calculated steady state rates for the main production and loss mechanisms of the three major ions are represented in Fig. 7 and 8 for the 1.5 and 8 Pa discharges respectively. Only the results corresponding to the k₁₈ value that gives a best agreement with the measured data are displayed for each pressure. Fig. 7 shows that in the 1.5 Pa discharge, Ar⁺ is produced by electron impact ionization of Ar atoms and is destroyed through neutralization at the wall or through reaction with H₂ (reaction (20)), which becomes the dominant destruction mechanism for H₂ fractions higher than 0.2. The main generation mechanisms of ArH⁺ are reactions (18) and (20). Overall, reaction (20) dominates, but for H₂ fractions higher than 0.6, reaction (18) becomes slightly preponderant. ArH⁺ ions are mainly lost in reaction with H₂ (reaction (21)) although for H₂ fractions lower than 0.2, wall neutralization is the main loss mechanism. H₃⁺ ions are essentially produced by collisions of ArH⁺ with H₂ over the whole mixture proportion range. Reaction (10) (H₂⁺ + H₂), which is the predominant H₃⁺ formation mechanism in many hydrogen plasmas, plays here a minor role. The H₃⁺ ions are destroyed in nearly equal amounts in collisions with Ar (reaction (18)) and through wall neutralization. Fig. 8 shows the important changes in the relative weight of the various production and destruction mechanisms when the discharge pressure is raised to 8 Pa. The ionization rate of Ar shows here a maximum for H₂ fractions lower than 0.2, which corresponds to the small maximum in the electron temperature depicted in Fig. 1 (upper-right panel). Reaction (20) now becomes the main mechanism of Ar⁺ loss for H₂ fractions larger than just 0.05. The ArH⁺ ion is largely formed through reaction (20) and lost in collisions with H₂ (reaction (21)) over the whole mixture fraction range. In contrast with the results for the 1.5 Pa discharge, reaction (18) (H₃⁺ + Ar) and flow to the wall play just a small role in the production and destruction of ArH⁺, respectively. The H₃⁺ ion is mostly formed by collisions of ArH⁺ with H₂ (reaction (21)) and is mainly lost through wall neutralization and to a minor extent through reaction (18).

Fig. 7 Rates of the most relevant formation (solid lines and plus signs in parentheses) and loss (dashed lines and minus signs in parentheses) processes for the major ions in the 1.5 Pa Ar/H₂ discharge as a function of the H₂ fraction.

Fig. 8 Same as Fig. 7, but for the 8 Pa discharge.

4.5 Comparison with previous works

As mentioned in the introduction, there are some recent studies^13,14,17 on the ion chemistry in Ar/H₂ inductively coupled rf discharges of variable mixture proportions and for pressures similar to those of the present work. Due to the different properties of the discharges, only an approximate comparison of those results with our work is possible, but it can still be meaningful considering that ionic chemistry is determined to a large extent by the electron temperature (which is closely related to the pressure) and by the gas composition. In comparison with the present work, the model of Kimura and Kasugai¹³ underestimates ArH⁺ production. It does not include reactions (18) and (17) (which produce ArH⁺) and takes a value of 1.5 × 10⁻⁹ cm³ s⁻¹ (twice the value used in our model) for the rate coefficient of reaction (21) that destroys ArH⁺ to form H₃⁺. Their calculated ion distributions at 2.8 and 8 Pa are always dominated either by Ar⁺ or by H₃⁺, with ArH⁺ being only the third ion in importance over the 0 to 50% range of H₂ fractions studied. The model of Hjartarson et al.¹⁴ also leads to a very low ArH⁺ concentration as compared with this work. The calculations performed for 1.33 Pa yield ion distributions that are always dominated either by Ar⁺ or by H₃⁺. The density of ArH⁺ is always less than half of that of the dominant ion. These authors used the same value as Kimura and Kasugai for the rate coefficient of reaction (21) (two times larger than the value we have used) and took k₁₈ = 1 × 10⁻¹¹ cm³ s⁻¹, which we found to be adequate for our 8 Pa measurements, but was too low for the 1.5 Pa experiments. Neither Kimura and Kasugai, nor Hjartarson et al. compared their model ion distributions with experimental data.

The detailed study of Sode et al.¹⁷ provided both experimental ion distributions and model simulations for a discharge pressure of 1 Pa (T_e = 3 to 4 eV). The model calculations covered the whole range of mixture proportions and the measurements were performed for 0.28 to 1 H₂ fraction range. The experimental distributions were dominated by ArH⁺, with Ar⁺ being the second ion in abundance. The measured H₃⁺ densities were always very low, even for the highest H₂ fractions. In their model, the authors used the rate coefficients recommended by Anicich³² for the relevant ArH⁺ reactions. Specifically, they took k₁₈ = 3.65 × 10⁻¹⁰ cm³ s⁻¹, one of the values used in the present work. The simulations¹⁷ led to appreciably higher densities of H₃⁺ and lower densities of ArH⁺ than their experiments. The reasons for the disagreement are not clear. Sode et al.¹⁷ noted that k₂₁ ∼ 0 would bring the simulations in much better accordance with their measurements and questioned the reliability of the recommended value³² (6.3 × 10⁻¹⁰ cm³ s⁻¹). This conclusion is however not warranted. As indicated above, k₂₁ has been measured by several groups^32,55,67 using different methods and consistently high values have been derived. In our lower pressure experiments, carried out for conditions of T_e and discharge pressure comparable to those of Sode et al.,¹⁷ the simulations using the recommended rate coefficients lead to a reasonably good agreement with the measurements (see the two lower panels of Fig. 2). Moreover, it is worth noting that the agreement between our experimental data and the model simulations of Sode et al.¹⁷ is reasonable, given the differences between the two experiments.

In the diffuse interstellar cloud model used by Schilke et al.,² ArH⁺ is essentially produced by collisions of H₂ with Ar⁺ (reaction (20)), which is in turn generated in the ionization of Ar atoms by cosmic rays or X-rays. Once formed, ArH⁺ is mostly lost in proton transfer collisions with O atoms and with H₂ molecules (reaction (21)). The authors remark that the unusually low rates for photodissociation and electron impact dissociative recombination of ArH⁺ enhance the survival of the ion in the diffuse ISM. For molecular hydrogen fractions, 2[H₂]/[H], larger than 10⁻⁴, collisions with H₂ (reaction (21)) are by far the preponderant mechanism for ArH⁺ destruction. As graphically expressed by Schilke et al.,² ArH⁺ is a molecule that paradoxically abhors molecular clouds. Reactions (20) and (21) are also the main production and destruction mechanisms of ArH⁺ in most of the plasmas studied in the present work and the abhorrence of ArH⁺ for H₂ is clearly seen in the ion distributions of our 8 Pa discharge (middle panel of Fig. 3). Reaction (18) (H₃⁺ + Ar), which is found to be an important source of ArH⁺ in many plasmas, such as the low pressure discharges in this work, is also included in the astrochemical model of Schilke et al., but with a very low rate coefficient (8 × 10⁻¹⁰ exp(−6400 K/T) cm³ s⁻¹), which seems appropriate for the vibrationally relaxed H₃⁺ expected in diffuse cloud sources. In other environments like the knots and filaments of the Crab Nebula, where ArH⁺ was first identified,¹ internal excitation of H₃⁺ by warm electrons may increase the relevance of this reaction.

5. Summary and conclusions

The ion chemistry in cold Ar/H₂ plasmas has been investigated in hollow cathode discharges. The experiments have been carried out for total pressures of 1.5 and 8 Pa, and spanning the whole range of [H₂]/([H₂] + [Ar]) ratios for each of the two pressures. A simple kinetic model, which takes the measured electron temperatures and densities as input parameters, has been used to rationalize the experimental data and to identify the main reaction mechanisms.

Three species, Ar⁺, ArH⁺ and H₃⁺, have been always found to dominate the measured ion distributions, but their relative densities vary markedly with pressure and with the Ar/H₂ mixture proportion. Special attention has been paid to the chemistry of ArH⁺. This ion was prevalent in the range 0.3 < [H₂]/([H₂] + [Ar]) < 0.7 in the 1.5 Pa discharge, but its predominance became restricted to [H₂]/([H₂] + [Ar]) < 0.04 in the 8 Pa plasma.

The kinetic model reveals two key factors for the ion chemistry in these plasmas: Electron temperature and the equilibrium of the process H₃⁺ + Ar ⇄ ArH⁺ + H_2. Electron temperature, which is basically a function of plasma pressure, determines the rates of formation of the primary plasma ions (Ar⁺ and H₂⁺) that start the ion-molecule chemistry. The rate of formation of Ar⁺ is always 6 to 7 times larger than that of H₂⁺, and Ar⁺ is the dominant primary ion up to very high H₂ fractions. Electron temperature decreases roughly from 3 eV to 2 eV when the discharge pressure is increased from 1.5 Pa to 8 Pa. As a result, the ionization rates of Ar and H₂ drop by a factor of ≈30 and the ions produced through ion-molecule chemistry (ArH⁺ and H₃⁺) gain in importance as compared with those directly formed by electron impact. Collisions of Ar⁺ with H₂ lead to an efficient production of ArH⁺. This ion can then give rise to H₃⁺ in subsequent collisions with H₂. The ratio between ArH⁺ and H₃⁺ depends strongly on the rate of the H₃⁺ + Ar → ArH⁺ + H₂ reaction, which is endothermic and should be slow for ground state reactants, but becomes exothermic and should be much faster for an internal excitation of H₃⁺ larger than 0.55 eV.

Our experiments and model simulations strongly suggest that H₃⁺ has an appreciable degree of internal excitation in the lower pressure (1.5 Pa) plasma and that this excitation is largely quenched in the higher pressure (8 Pa) discharge. This interpretation reconciles conflicting literature values for the rate coefficient of the H₃⁺ + Ar reaction and leads to a reasonably good agreement between our measurements and model simulations over the whole range of conditions sampled. On the other hand, the results corroborate the comparatively large (>5 × 10⁻¹⁰ cm³ s⁻¹) rate coefficient for the exothermic reaction ArH⁺ + H₂ → Ar + H₃⁺, currently accepted in the literature, but questioned in a recent work. In the absence of a mechanism that regenerates ArH⁺ like the mentioned [H₃⁺]* + Ar reaction, the argonium ion is efficiently removed in H₂ containing media, even if H₂ is present in very small amounts. This behavior, which is exemplified in our higher pressure discharge, was also reported in previous spectroscopic investigations carried out in comparable discharge cells, and is also displayed by the astrochemical models applied to the recent observations of ArH⁺ in the interstellar medium.

The results of this study invite further theoretical and experimental work on the detailed state-specific dynamics of the processes involved in the production, destruction, excitation and quenching of ArH⁺ and H₃⁺.

Acknowledgements

The authors acknowledge the financial support from the Spanish MINECO through the Consolider Astromol project, CSD2009-00038. VH and IT acknowledge additional support through grant FIS2010-16455 and FIS2013-48087-C2-1-P. JLD and MC acknowledge additional support through grant FIS2012-38175. MJR acknowledges funding from the FPI program of the MICINN. We also thank the European Research Council for additional support under ERC-2013-Syg 610256-Nanocosmos. Our skillful technicians J. Rodríguez and M.A. Moreno are gratefully acknowledged.

References

1. M. J. Barlow, B. M. Swinyard, P. J. Owen, J. Cernicharo, H. L. Gomez, R. J. Ivison, O. Krause, T. L. Lim, M. Matsuura, S. Miller, G. Olofsson and E. T. Polehampton, Science, 2013, 342, 1343–1345.
2. P. Schilke, D. A. Neufeld, H. S. P. Müller, C. Comito, E. A. Bergin, D. C. Lis, M. Gerin, J. H. Black, M. Wolfire, N. Indriolo, J. C. Pearson, K. M. Menten, B. Winkel, Á. Sánchez-Monge, T. Möller, B. Godard and E. Falgarone, Astron. Astrophys., 2014, 566, A29.
3. R. F. G. Meulenbroeks, R. A. H. Engeln, M. N. A. Beurskens, R. M. J. Paffen, M. C. M. Vandesanden, J. A. M. Vandermullen and D. C. Schram, Plasma Sources Sci. Technol., 1995, 4, 74–85.
4. S. B. Radovanov, J. K. Olthoff, R. J. Vanbrunt and S. Djurovic, J. Appl. Phys., 1995, 78, 746–757.
5. R. S. Mason, P. D. Miller and I. P. Mortimer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 7462–7472.
6. J. T. Gudmundsson, Plasma Sources Sci. Technol., 1998, 7, 330–336.
7. J. T. Gudmundsson, Plasma Sources Sci. Technol., 1999, 8, 58–64.
8. T. G. Beuthe and J. S. Chang, Jpn. J. Appl. Phys., Part 1, 1999, 38, 4576–4580.
9. A. Bogaerts and R. Gijbels, J. Anal. At. Spectrom., 2000, 15, 441–449.
10. A. Bogaerts and R. Gijbels, Spectrochim. Acta, Part B, 2002, 57, 1071–1099.
11. A. Bogaerts, J. Anal. At. Spectrom., 2008, 23, 1476–1486.
12. E. Neyts, M. Yan, A. Bogaerts and R. Gijbels, J. Appl. Phys., 2003, 93, 5025–5033.
13. T. Kimura and H. Kasugai, J. Appl. Phys., 2010, 107, 083308.
14. A. T. Hjartarson, E. G. Thorsteinsson and J. T. Gudmundsson, Plasma Sources Sci. Technol., 2010, 19, 065008.
15. I. Mendez, I. Tanarro and V. J. Herrero, Phys. Chem. Chem. Phys., 2010, 12, 4239–4245.
16. M. Sode, T. Schwarz-Selinger and W. Jacob, J. Appl. Phys., 2013, 113, 093304.
17. M. Sode, T. Schwarz-Selinger and W. Jacob, J. Appl. Phys., 2013, 114, 063302.
18. V. D. Hodoroaba, V. Hoffmann, E. B. M. Steers and K. Wetzig, J. Anal. At. Spectrom., 2000, 15, 1075–1080.
19. K. Newman, R. S. Mason, D. R. Williams and I. P. Mortimer, J. Anal. At. Spectrom., 2004, 19, 1192–1198.
20. A. Martin, A. Menendez, R. Pereiro, N. Bordel and A. Sanz-Medel, Anal. Bioanal. Chem., 2007, 388, 1573–1582.
21. S. Weyler and A. Bengtson, J. Anal. At. Spectrom., 2010, 25, 849–855.
22. F. L. Tabares and D. Tafalla, J. Vac. Sci. Technol., A, 1996, 14, 3087–3091.
23. C. V. Budtz-Jørgensen, P. Kringhoj and J. Bottiger, Surf. Coat. Technol., 1999, 116, 938–943.
24. C. V. Budtz-Jørgensen, P. Kringhoj, J. F. Nielsen and J. Bottiger, Surf. Coat. Technol., 2001, 135, 299–306.
25. P. Saikia, B. Kakati and B. K. Saikia, Phys. Plasmas, 2013, 20, 103505.
26. N. Laidani, R. Bartali, P. Tosi and M. Anderle, J. Phys. D: Appl. Phys., 2004, 37, 2593–2606.
27. I. B. Denysenko, S. Xu, J. D. Long, P. P. Rutkevych, N. A. Azarenkov and K. Ostrikov, J. Appl. Phys., 2004, 95, 2713–2724.
28. C. F. Yeh, T. J. Chen, C. Liu, J. T. Gudmundsson and M. A. Lieberman, IEEE Electron Device Lett., 1999, 20, 223–225.
29. N. Fox-Lyon, G. S. Oehrlein, N. Ning and D. B. Graves, J. Appl. Phys., 2011, 110, 104314.
30. K. Ostrikov, E. C. Neyts and M. Meyyappan, Adv. Phys., 2013, 62, 113–224.
31. K. Ostrikov, H. J. Yoon, A. E. Rider and S. V. Vladimirov, Plasma Processes Polym., 2007, 4, 27–40.
32. V. G. Anicich, J. Phys. Chem. Ref. Data, 1993, 22, 1469–1569.
33. J. W. Brault and S. P. Davis, Phys. Scr., 1982, 25, 268–271.
34. N. N. Haese, F. S. Pan and T. Oka, Phys. Rev. Lett., 1983, 50, 1575–1578.
35. J. W. C. Johns, J. Mol. Spectrosc., 1984, 106, 124–133.
36. K. B. Laughlin, G. A. Blake, R. C. Cohen and R. J. Saykally, J. Chem. Phys., 1989, 90, 1358–1361.
37. J. M. Brown, D. A. Jennings, M. Vanek, L. R. Zink and K. M. Evenson, J. Mol. Spectrosc., 1988, 128, 587–589.
38. R. R. Filgueira and C. E. Blom, J. Mol. Spectrosc., 1988, 127, 279–280.
39. M. Cueto, J. Cernicharo, M. J. Barlow, B. M. Swinyard, V. J. Herrero, I. Tanarro and J. L. Doménech, Astrophys. J., Lett., 2014, 783, L5.
40. M. Castillo, I. Mendez, A. M. Islyaikin, V. J. Herrero and I. Tanarro, J. Phys. Chem. A, 2005, 109, 6255–6263.
41. I. Mendez, F. J. Gordillo-Vazquez, V. J. Herrero and I. Tanarro, J. Phys. Chem. A, 2006, 110, 6060–6066.
42. I. Tanarro, V. J. Herrero, A. M. Islyaikin, I. Mendez, F. L. Tabares and D. Tafalla, J. Phys. Chem. A, 2007, 111, 9003–9012.
43. I. Tanarro and V. J. Herrero, Plasma Sources Sci. Technol., 2009, 18, 034007.
44. M. Castillo, V. J. Herrero and I. Tanarro, Plasma Sources Sci. Technol., 2002, 11, 368–376.
45. M. A. Lieberman and A. J. Lichtenberg, Principles of Plasma Discharges and Materials Processing, Wiley and sons, 2005.
46. F. C. Parra-Rojas, M. Passas, E. Carrasco, A. Luque, I. Tanarro, M. Simek and F. J. Gordillo-Vazquez, J. Geophys. Res.: Space Phys., 2013, 118, 4649–4661.
47. D. L. Albritton, At. Data Nucl. Data Tables, 1978, 22, 1–101.
48. M. Capitelli and C. Gorse, IEEE Trans. Plasma Sci., 2005, 33, 1832–1844.
49. M. Capitelli, M. Cacciatore, R. Celiberto, O. De Pascale, P. Diomede, F. Esposito, A. Gicquel, C. Gorse, K. Hassouni, A. Laricchiuta, S. Longo, D. Pagano and M. Rutigliano, Nucl. Fusion, 2006, 46, S260–S274.
50. V. Gencheva, R. Djulgerova, V. Mihailov, T. Dohnalik and Z. L. Petrovic, in First International Workshop on Nonequilibrium Processes in Plasma Physics and Studies of Environment, ed. Z. L. Petrovic, G. Malovic, M. Tasic and Z. Nikitovic, Iop Publishing Ltd, Bristol, 2007, vol. 71.
51. M. Jimenez-Redondo, E. Carrasco, V. J. Herrero and I. Tanarro, Phys. Chem. Chem. Phys., 2011, 13, 9655–9666.
52. R. D. Smith and J. H. Futrell, Int. J. Mass Spectrom. Ion Processes, 1976, 20, 33–41.
53. C. R. Blakley, M. L. Vestal and J. H. Futrell, J. Chem. Phys., 1977, 66, 2392–2399.
54. A. B. Rakshit and P. Warneck, J. Chem. Phys., 1981, 74, 2853–2859.
55. H. Villinger, J. H. Futrell, F. Howorka, N. Duric and W. Lindinger, J. Chem. Phys., 1982, 76, 3529–3534.
56. B. R. Rowe, A. Canosa and V. Lepage, Int. J. Mass Spectrom. Ion Processes, 1995, 149, 573–596.
57. M. T. Bowers and D. D. Elleman, J. Chem. Phys., 1969, 51, 4606–4617.
58. A. E. Roche, M. M. Sutton, D. K. Bohme and H. I. Schiff, J. Chem. Phys., 1971, 55, 5480–5484.
59. J. E. Pollard, L. K. Johnson, D. A. Lichtin and R. B. Cohen, J. Chem. Phys., 1991, 95, 4877–4893.
60. J. J. Leventhal and L. Friedman, J. Chem. Phys., 1969, 50, 2928–2931.
61. J. K. Kim, L. P. Theard and W. T. Huntress Jr, Int. J. Mass Spectrom. Ion Phys., 1974, 15, 223–244.
62. C. W. Eaker and G. C. Schatz, J. Phys. Chem., 1985, 89, 2612–2620.
63. K. M. Ervin and P. B. Armentrout, J. Chem. Phys., 1985, 83, 166–189.
64. M. Sizun, J. B. Song and E. A. Gislason, J. Chem. Phys., 2002, 116, 2888–2895.
65. S. Chapman, J. Chem. Phys., 1985, 82, 4033–4043.
66. V. Kokoouline, A. Faure, J. Tennyson and C. H. Greene, Mon. Not. R. Astron. Soc., 2010, 405, 1195–1202.
67. D. K. Bedford and D. Smith, Int. J. Mass Spectrom. Ion Processes, 1990, 98, 179–190.

---