Real-time control of inertial focusing in microfluidics using dielectrophoresis (DEP)
Abstract
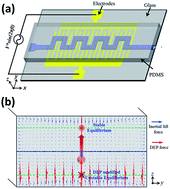
In this paper, we propose a novel hybrid microfluidic device, for the first time, which integrates and fully couples both dielectrophoresis (DEP) and inertial focusing. A DEP force is coupled with inertial lift force to adjust particle's equilibrium position in the vertical direction in real time. The focusing pattern and position of the particles along the horizontal plane can be concurrently adjusted by adjusting their vertical position with DEP forces. The magnitude of secondary flow drag dramatically increases when particles are levitated towards the centre of the channel in the vertical direction. The paper analytically and experimentally investigates the mechanism of this tuneable DEP-inertial microfluidic device. The proposed hybrid device possesses the advantages of both DEP and inertial microfluidic devices, working in a high-throughput manner, as well as having precise controllability in real-time. This DEP-inertial microfluidic device is potentially a versatile and robust platform for a feedback-controlled manipulation and separation of particles and cells.

 Please wait while we load your content...
Please wait while we load your content...