Effect of dispersed colloidal gold nanoparticles on the electrical properties of a columnar discotic liquid crystal

Abstract

A dispersion of colloidal gold nanoparticles (GNPs) in a triphenylene-based discotic liquid crystal (DLC), namely 2,3,6,7,10,11-hexabutyloxytriphenylene (HAT4), possessing a hexatic plastic columnar phase (Col_hp) phase, has been studied by differential scanning calorimetry, polarized light microscopy, UV-Vis absorption spectroscopy, X-ray diffraction and dielectric spectroscopy. GNPs have been dispersed at three different concentrations in pure HAT4 viz. 0.2, 0.6 and 1.2 wt%. It has been observed that with the increase of GNPs concentration, the Col_hp–isotropic liquid transition temperature decreases substantially but the crystal–Col_hp transition temperature does not changes significantly. Electrical conductivity increases by at least five orders of magnitude for the highest concentration of GNPs (1.2 wt%) as compared to the pure material i.e. HAT4. Observed results suggest that although extremely low concentrations of GNPs are not very useful, a moderate concentration is highly useful for increasing the conductivity of the Col_hp phase and also to implant surface plasmon resonance. These results may be exploited to enhance the efficiency of electro-optical devices by using HAT4–GNPs composites.

---

1. Introduction

Discotic liquid crystals (DLCs) are important functional materials which find application as one-dimensional conductors, light emitting diodes, photoconductors and photovoltaic solar cells.^1–4 They are generally made of a central aromatic core flanked by aliphatic chains. Appropriately substituted disc shaped molecules arrange themselves in ordered columns by various supramolecular interactions such as π–π interactions, charge-transfer interactions, dipolar or quadrapolar interactions, metal coordination and hydrogen bonding etc. Due to the strong π–π interaction between the aromatic cores and the weak interaction between the flexible aliphatic chains, the molecules can stack one over the other, forming columns. Typical column–column distance in the columnar hexagonal phase is around 2–4 nm depending on the aliphatic chain length and the core–core distance within the column is around 0.35 nm.⁵ Strong intracolumnar interaction and weak intercolumnar interaction contribute to the quasi-one-dimensional electrical conductivity along the columns. The quasi-one-dimensional electrical conductivity in these discotic systems has been proposed for diverse applications in the areas including solar cells, molecular electronics, photovoltaic cells, and organic light emitting diodes.^6,7 The efficiency of such devices depends on the band gap of the materials, which is typically ∼4 eV for the DLCs and therefore behave as insulator at normal conditions. On the other hand, DLCs may be converted to useful semiconductors by doping with either electron rich or electron deficient molecules into the supramolecular order of the liquid crystalline phase. It is well documented that conductivity along the columns in a columnar mesophase is several orders greater as compared to its value perpendicular to the columns.⁵ Especially few groups have proposed the increase in efficiency of photovoltaic cells by using discotic liquid crystalline materials, because disc shape molecules can allow-quasi one dimensional transport of charge carrier mobility.^8,9

Liquid crystal-nano particle (LC-NP) composites^10,11 have emerged as a multidisciplinary field of research and attracts great attention of scientists from the field of soft matter research. Nano particles can effectively be used to tune the properties of liquid crystals.^12,13 Innumerable reports exist in which NPs have been dispersed in DLCs,^14–18 nematic LCs^19–22 and FLCs.^23,24 Also NPs have been dispersed in the Smectic-A phase of a de Vries liquid crystalline material.²⁵ Metal nano particles (MNPs) have received much attention because of their excellent optical, electronic and magnetic properties.^26–28 MNPs such as gold, silver and copper are important because of the surface plasmonic resonance (SPR).^29–32 For these MNPs, the localized SPR falls in the visible region. Therefore, these MNPs are suitable for optical sensing of change in refractive index and are used in optical devices. The use of MNPs to tailor LCs properties^33,34 has opened several avenues for application in opto-electronic devices. Several theoretical and experimental investigations on colloidal particles dispersed in liquid crystals have been carried out, where in spherical shape of collides and self assembling nature of liquid crystals have played important role. Kumar et al.³⁵ have reported a relatively modest increase in the conductivity of a discotic liquid crystal on doping with 20–50% (w/w) GNPs. Holt et al.³⁶ have reported 10⁶ fold enhancement in the conductivity of the columnar discotic HAT7 doped with 1% (w/w) of GNP. Kavitha et al.³⁷ have reported the photoconductivity of GNPs doped hexa-alkoxytriphenylene derivatives in the region of 10⁻⁴ to 10⁻⁵ S m⁻¹, which is five orders of magnitude higher than that of the undoped compounds. The intercalation of GNPs into the DLCs may leads to novel composites with interesting properties useful for many device applications.^38,39

In view of the above reports, we incorporated colloidal gold nano particles in a discotic liquid crystal and determined the physical parameters of these discotic liquid crystal-nano composites. Fig. 1 shows molecular structure of the triphenylene based discotic liquid crystal hexabutyloxytriphenelene (HAT4) possessing hexatic plastic columnar phase (Col_hp).^40–42 The colloidal gold nano particles (non functionalized reactant free standard gold nano particles, >99% reactant free, displaying a light reddish colour) used in the present study with the size of 5 nm diameter have been procured from Sigma-Aldrich, USA. In the present paper, we report results based on differential scanning calorimetry, polarized light microscopy, UV-Vis spectroscopy, X-ray diffraction (XRD) and dielectric spectroscopies of colloidal GNPs dispersed in HAT4 for three different concentrations.

Fig. 1 Molecular structure of 2,3,6,7,10,11-hexabutoxytriphenylene (HAT4).

2. Experimental details

The HAT4–GNP composites have been prepared by adding weighted percentage of GNPs in the pure HAT4. The HAT4 and GNPs have been dissolved in chloroform (CHCl₃) and ultrasonicated for about two hours to obtain uniform dispersion. Slow evaporation of the solvent, resulted in the formation of desired dispersion. We prepared samples with three different compositions i.e. 0.2, 0.6 and 1.2 wt% of GNPs in HAT4. The thermodynamical study of pure and dispersed samples has been carried out with the help of differential scanning calorimeter (DSC) of NETZSCH model DSC-200-F3-Maia. Peak transition temperature (T_P in °C), transition enthalpy (ΔH in J g⁻¹) and transition entropies (ΔS in J g⁻¹ K⁻¹) for various transitions have been determined from the DSC studies, which was operated at various scanning rates in the heating and cooling cycles. The optical textural studies of the mesophase were carried out with the help of polarized light microscope (PLM) coupled with a hot stage (Instec, MK 1000). The sample was heated to the isotropic liquid phase, and then defects were imaged during the cooling cycles in order to get stabilized textures. UV-Vis absorbance spectra were recorded with UV-Vis Spectrophotometer of Shimadzu (model UV-1800) in the wavelength region of 190 nm to 900 nm. CHCl₃ was used as a reference in a standard quartz cells having 10 mm path length. The dielectric studies of the samples were carried out on the homeotropic geometry wherein plane of discotic molecules is parallel to the electrodes' surfaces. The sandwiched type (capacitors) cells were made using two optically flat glass substrates coated with indium tin oxide (ITO) layers. The cell thickness was fixed by placing two Mylar spacers (thickness 10 μm) between the glass plates. System was then clamped with a sample holder in order to avoid use of any adhesive to hold the plates. These cells have been used for the optical textures studies as well. The samples were introduced via capillary action by heating to the isotropic liquid phase. Slow cooling of sample from the isotropic phase generally yields spontaneous homeotropic alignment (column axis normal to the glass plates) of DLCs in thin cells as it is minimum energy configuration. Unless mentioned otherwise dielectric data were collected during the cooling cycle wherein alignment of the molecules is expected to be better than the heating cycle. Dielectric data have been acquired by using the Alpha-A high performance frequency analyzer from Nova Control technologies coupled with two-wire Impedance Interface ZG2 in the frequency range of 10 Hz to 40 MHz. For the dielectric studies also temperature of the sample was controlled with the help of Instec hot stage having an accuracy of ±0.1 °C. Temperature near the sample was determined by measuring thermo emf with the help of a six and half digit multi meter of Agilent (model 34410A) with the accuracy of ±0.1 °C. The experiments were carried out in the temperature range of 30 °C to 160 °C. Detailed methodology and necessary mathematical equations to obtain the dielectric permittivity (ε′), loss (ε′′) and conductivity (σ) of the materials can be seen from our earlier publications.^21,43

Total conductivity of the material follows general equation⁴⁴

σ = σ_i + Af^m (1)

Where A is the pre-exponential factor and m is the fractional exponent lying between 0 and 1. σ_i is the ionic conductivity. At low frequencies (<1 kHz), second (dipolar) part (Af^m) of right hand side is negligible⁴⁵ and hence total conductivity is composed of only ionic part i.e. σ = σ_i

Small angle X-ray scattering (SAXS) studies were carried out using an X-ray diffractometer (Rigaku, UltraX 18) operating at 50 kV and 80 mA current having Cu-Kα radiation of the wavelength of 1.54 Å. The samples was filled in a capillary and then sealed. It was then heated to 100 °C and 120 °C giving exposure at these temperatures before going to isotropic liquid phase at 155 °C.

3. Results and discussion

3.1 DSC studies

DSC was operated at various scanning rates between 2.5 °C min⁻¹ and 15.0 °C min⁻¹ in the heating and cooling cycles. Typical DSC thermograms for pure and composites are shown in Fig. 2a for the heating and in Fig. 2b for the cooling cycles at the scan rate of 5.0 °C min⁻¹. Samples have been given 5 thermal cycles before collecting fair data in order to stabilize the systems. As usual, it has been observed that transitions temperatures vary linearly with the scanning rate with opposite slopes in the heating and cooling cycles. Extrapolated transition temperatures at the (hypothetical) scan rate of 0 °C min⁻¹ have been obtained through least square fit.⁴⁶ The transition temperatures thus obtained are supposed to be the true transition temperatures under the condition of thermal equilibrium and are identical during heating and cooling cycles for an enantiotropic transition i.e. they do not represent hysteresis effect during heating and cooling cycles. For this reason, Iso–Col_hp and Col_hp–Iso transitions are equivalent. Extrapolated transition temperatures at the scan rate of 0 °C min⁻¹ give following phase sequences in the studied samples.

Fig. 2 DSC thermograms for the pure and dispersed samples during heating (a) and cooling (b) cycles at the scan rate of 5 °C min⁻¹. Curve (1) for HAT4, (2) for HAT4 + 0.2 wt% GNPs, (3) for HAT4 + 0.6 wt% GNPs and (4) for HAT4 + 1.2 wt% GNPs.

Pure HAT4: Cr (87.2 °C) Col_hp–(144.8 °C)–Iso–(144.8 °C)–Col_hp–(81.0 °C)–Cr′

HAT4 + 0.2 wt% GNPs: Cr (87.0 °C) Col_hp–(137.2 °C)–Iso–(137.2 °C)–Col_hp–(80.0 °C)–Cr′

HAT4 + 0.6 wt% GNPs: Cr (87.3 °C) Col_hp–(131.6 °C)–Iso–(131.6 °C)–Col_hp–(78.7 °C)–Cr′

HAT4 + 1.2 wt% GNPs: Cr (88.0 °C) Col_hp–(118.9 °C)–Iso–(118.9 °C)–Col_hp–(78.9 °C)–Cr′

Here Iso, Col_hp and Cr represent isotropic liquid, hexatic plastic columnar and crystal phases respectively. During the cooling cycle, samples show poly crystalline behavior i.e. some more phase transitions occurs after Col_hp–Cr′ transition (see Fig. 2b) and hence Cr′ and Cr are not same. Further, Cr′–Cr transition generally does not depend upon scan rate. Various transitions have been confirmed by the optical texture studies under PLM as well. As may be seen from the DSC thermograms as well as from the above data, with the increase of the GNPs concentration, Col_hp–Iso transition temperature decreases but the Cr–Col_hp transition temperature does not change significantly. DSC thermograms show interesting results (see Fig. 2). It has been observed that the height and width of the peaks for the Col_hp–Iso transition changes with the concentration of GNPs. Peak height has gradually decreased whereas width of the peak has increased in such a way that ΔH of the transition show continuous decrease (see Table 1) with the increasing concentration of GNPs. Here it is important to mention that ΔH for the Cr–Col_hp transition i.e. enthalpy of the melt has also decreased with the increasing concentration of GNPs but here changes are small as compared to the Col_hp–Iso transition. Entropies of the transitions (ΔS) which represent change in order (or disorder) have also been determined for various transitions and are listed in Table 1.

Table 1 The peak transition temperature (T_P in °C), transition enthalpy (ΔH in J g⁻¹), and transition entropies (ΔS in mJ g⁻¹ K⁻¹), for various transitions deduced from DSC studies for HAT4, HAT4 + 0.2 wt% GNPs, HAT4 + 0.6 wt% GNPs and HAT4 + 1.2 wt% GNPs at the scan rate of 5 °C min⁻¹

System	HAT4			0.2 wt% GNPs			0.6 wt% GNPs			1.2 wt% GNPs
	TP	ΔH	ΔS	TP	ΔH	ΔS	TP	ΔH	ΔS	TP	ΔH	ΔS
Heating cycle
Cr–Colhp	88.0	34.2	94.6	88.2	33.1	91.5	88.0	30.2	83.6	89.2	19.6	54.0
Colhp–Iso	145.9	28.3	67.6	138.4	19.0	46.1	133.4	15.9	39.1	122.7	3.7	9.3
Cooling cycle
Iso–Colhp	143.3	28.0	67.2	135.3	19.4	47.4	130.6	15.3	37.8	117.8	44.4	1.1
Colhp–Cr′	79.0	3.6	10.2	77.9	3.4	9.6	78.1	3.1	8.8	77.7	2.0	5.7

---

While going from Cr to Iso phase, ΔH and hence ΔS is positive at transitions and consequently order is decreasing (or disorder is increasing) and is least (disorder is maximum) in the isotropic liquid phase. Here it is important to mention that in the case of HAT4, ΔH for Col_hp mesophase–Iso transition is very high as compared to mesophase–Iso transitions of other DLCs or rod shaped liquid crystals. It means Col_hp of the HAT4 is highly ordered (rigid) structure as compared to the nematic or smectic mesophases of rod shaped liquid crystals. This justifies the name plastic crystal for the Col_hex of the HAT4.⁴² If we assume that Iso phase is completely disordered (it can be taken other way also i.e. crystal phase is perfectly ordered) then magnitude ΔH at Iso–Col_hp transition will yield relative order (rigidity) of the Col_hp phase as compared to that of the Iso phase. Low magnitude of ΔH will represent Col_hp phase of low rigidity as compared to the case where ΔH is high at the Iso–Col_hp transition. For this reason it can be assumed that Col_hp phase of the 3rd composite i.e. HAT4 + 1.2% GNPs is least rigid (or better fluid) as compared to the pure HAT4.

3.2 Optical studies

Optical texture studies suggest that when the pure (HAT4) sample is taken in a thin (10 μm) cell, near perfect homeotropic alignment is obtained on very slow cooling from the Iso phase. Alignment thus obtained is stable throughout the Col_hp phase range, as confirmed by near dark field of view under the crossed polarizers (see Fig. 3a). Dark field of view is expected when optical (column) axis is parallel to the direction of the light propagation under the crossed polarizers' condition of the PLM. Such condition cancel out any chance of birefringence phenomena in the homeotropic aligned sample. In the case of composites (0.2 and 0.6 wt%), alignment does not seem perfect (see Fig. 3b). Here intensity of light is higher as compared to the pure system. However, for the composite having 1.2 wt% of GNPs, we again get dark field of view (see Fig. 3c) which is even darker than the texture of the pure sample. Fig. 3c converts to the texture shown in Fig. 3d after crystallization. Thus on the basis of intensity of light of the optical textures, we find that composite having 1.2 wt% of GNPs show best homeotropic alignment of the molecules. On this aspect, we will further discuss during the forthcoming sections while presenting dielectric and SAXS results.

Fig. 3 Optical textures (a) for HAT4, (b) for HAT4 + 0.2 wt% GNPs, (c) for HAT4 + 1.2 wt% GNPs at 100 °C in Col_hp phase and (d) for HAT4 + 1.2 wt% GNPs at 53 °C in Cr phase.

UV-Visible absorption spectroscopy is the most widely used method for characterizing the optical properties of nano particles. Absorbance studies in the UV-Visible region have been carried out on the DLC, GNPs and nano composites (see Fig. 4). The pure GNPs show absorbance maximum at 530 nm (see inset 1 of Fig. 4) which is due to surface plasmon resonance (SPR).⁴⁷ In the case of HAT4, the spectra show strong absorption at 279 nm and weak low energy excitations at 311 and 349 nm. The peak at 279 nm is assigned to the pure HAT4 molecules corresponding to a band gap of about 4.2 eV.⁴⁸ The above spectral bands have been interpreted to be due to the symmetrically allowed transitions in the discotic molecules.⁴⁹ After dispersion of GNPs, above peaks are shifted to 307 ± 2 nm, 345 ± 2 nm and 362 ± 1 nm respectively. In the case of the composite having 1.2 wt% of GNPs, a broad absorption peak is clearly visible at 518 nm (see inset 2 of Fig. 4) which is SPR peak of GNPs but here it shows blue shift of 12 nm as compared to that of the pure GNPs. In the case of composites having 0.2 and 0.6 wt% of GNPs, SPR effect is not convincingly visible because of the weak intensity due to the low concentration of GNPs. Broad range absorption in the visible region for GNPs dispersed in HAT4 makes the composite a potential candidate for photo voltaic applications and solar absorber.⁵⁰

Fig. 4 UV-Vis absorption spectra for the pure and dispersed samples. Curve (1) for HAT4, (2) for 0.2 wt% GNPs, (3) for 0.6 wt% GNPs and (4) for 1.2 wt% GNPs in HAT4. In the case of composites, low energy excitation peaks have been focused and hence high energy peaks have not been shown. Upper inset diagram shows spectra for GNPs, whereas lower inset shows the SPR peak for 1.2 wt% of GNPs in HAT4. For 0.2 and 0.6 wt% of GNPs, intensity of SPR peak is very weak and could not be convincingly visible.

3.3 Dielectric studies

Generally in the discotic materials, doping of nano particles (NPs) increases the conductivity throughout the isotropic and mesophases.^7,13 A similar effects has been observed by doping the GNPs in HAT4 in our case also but with some marked difference as compared to previous cases. The measured data taken during the cooling cycles are presented in Fig. 5. It has been observed that at the transition temperatures recorded by DSC (shown by vertical dashed lines in Fig. 5), conductivity plots either show discontinuity or change their slopes. The conductivity of pure HAT4 is of the order of 10⁻¹⁰ S m⁻¹ which is in agreement with the values reported in literature.⁵¹ The conductivity in the Col_hp has increased by about five orders of magnitude for the highest concentration (1.2 wt%) of GNPs. The variation of log σ with frequency in columnar hexagonal phase at 100 °C is shown in Fig. 5a and it follows the general eqn (1). σ_i and constants A and m of eqn (1) were determined by the fitting process. Variation of the ionic conductivity with temperature is shown in Fig. 5b. Enhancement of the ionic conductivity in Col_hp is almost same for 0.6 and 0.2 wt% of GNPs. It is important to mention here that in the case of composites having 0.6 and 0.2 wt% of GNPs, enhancement in the conductivity is almost uniform throughout the isotropic liquid and Col_hp phases except small decrement at Iso–Col_hp transition which is due to increase in the viscosity at the transition. However, in the case of the composite having 1.2 wt% of GNPs, conductivity has drastically increased while going to Col_hp phase from the isotropic liquid phases (see Fig. 5b). This is clear evidence of very good alignment of molecules in the columns. At 80.6 °C the conductivity of pure HAT4 is 5.9 × 10⁻¹⁰ S m⁻¹ and that of the composites are 1.8 × 10⁻⁷ S m⁻¹ (0.2 wt%) and 8.1 × 10⁻⁸ S m⁻¹ (0.6 wt%). Towards higher temperature side at 99.9 °C, these values are respectively enhanced to 1.0 × 10⁻⁹ S m⁻¹, 3.4 × 10⁻⁷ S m⁻¹ and 1.1 × 10⁻⁷ S m⁻¹. The ionic conductivity of the composites having 1.2 wt% GNPs is 1.5 × 10⁻⁵ S m⁻¹ at 80.6 °C and 2.5 × 10⁻⁵ S m⁻¹ at 99.9 °C.

Fig. 5 Variation of total conductivity with frequency (a) and variation of the ionic conductivity with the temperature (b) for pure and dispersed samples. Curve (1) for HAT4, (2) for HAT4 + 0.2 wt% GNPs, (3) for HAT4 + 0.6 wt% GNPs and (4) for HAT4 + 1.2 wt% GNPs in HAT4. The vertical dashed lines denote the extrapolated transition temperatures obtained from the DSC studies.

Variation of the ionic conductivity with inverse of the temperature in Col_hp phase is shown in Fig. 6. The ionic conductivity follows the Arrhenius equation,

σ_i = A exp(−W_a/kT) (2)

where k is the Boltzmann constant and W_a is the activation energy. The slopes of the plots of log(σ_i) versus inverse of the temperature (and hence W_a) were obtained by the method of least square fit as shown in Fig. 6. Values of W_a suggests that it is almost of the same magnitude (15 ± 2 kJ mol⁻¹) for pure HAT4, and composites having 0.2 and 0.6 wt% GNPs. High value of the activation energy in the Col_hp phase is apparently due to its rigid structure (plastic nature). However, in the case of the composite having 1.2 wt% GNPs, W_a has drastically decreased to 5 kJ mol⁻¹. As discussed earlier (section 3.1), this again shows that Col_hp phase of the composite having 1.2 wt% GNPs has better fluidity as compared to the other studied systems and this enhances the migration of the charge carriers.

Fig. 6 Variation of the ionic conductivity with inverse of temperature (Arrhenius plots). Curve (1) for HAT4, (2) for HAT4 + 0.2 wt% GNPs, (3) for HAT4 + 0.6 wt% GNPs and (4) for HAT4 +1.2 wt% GNPs.

The ionic conductivity of columnar discotic systems may arise either due to the hopping of the holes or electron tunneling mechanism. In the present case, due to the facile formation of the radical cations of HAT4, the hopping mechanism should be favoured, i.e. HAT4 radical cations are the dominant charge carriers in the composites.⁵² In the present case, GNPs entered in DLC matrix and enhance ionic conductivity in general. However, enhance of the ionic conductivity is maximum for the composite having 1.2 wt% of GNPs in its Col_hp phase. These nano particles favour hopping mechanism and this is drastically enhanced when molecules are well organized in the columns in the case of composite having 1.2 wt% GNPs. As concluded by the optical texture studies, conductivity data also suggest that Col_hp phase is well organized in the case of composite having 1.2 wt% GNPs. Conductivity is lowest in pure HAT4, moderate in the composites having 0.2 and 0.6 wt% GNPs and highest in the case of composite having 1.2 wt% GNPs (see Fig. 5b). Lowest value of the conductivity in pure HAT4 is due to the low charge carriers coupled with the high rigidity of the Col_hp phase. In the case of composites having 0.2 and 0.6 wt% GNPs, conductivity has enhanced (as compared to pure HAT4) due to GNPs but still poor as compared to the composite having 1.2 wt% GNPs. This is because of the poor organization of the Col_hp phase in these two systems. Now question is why it is so? Observed results suggest that presence of GNPs disturbs spontaneous columnar organization of the discotic molecules and randomness is highest in the isotropic liquid phase. When system goes to the Col_hp phase while cooling, discotic molecules try to form columnar structure but they do not find it easy in the case of composites having 0.2 and 0.6 wt% GNPs due to high rigidness (situation like freezing of the structure). However, in the case of the composite having 1.2 wt% GNPs, low rigidity of the Col_hp phase (readers please recall discussion of the Section 3.1), better columnar structure is formed on slow cooling as compared to the composites having 0.2 and 0.6 wt% GNPs. This is clearly evident from the conductivity results and supported by the optical texture studies.

The variation of (static) dielectric permittivity with temperature is shown in Fig. 7. Discontinuity or change of the slope of the permittivity values at Iso–Col_hp transitions is indicative of alignment of discs in the columns. These changes agree with the transition temperatures obtained from the DSC (see dashed vertical lines in Fig. 7). Slow cooling of sample from the isotropic phase is expected to yield good homeotropic alignment during the mesophase. In the case of composite having 1.2 wt% GNPs, a small discontinuity of the permittivity has been detected at ∼105 °C (see curve 4 of Fig. 7) when molecules are perfectly arranged in the columns and at this stage conductivity reaches to maximum value (see curve 4 of Fig. 5b). This temperature represents complete end of the Iso–Col_hp DSC peak i.e. columnar structure is fully developed (as expected) only after the complete thermodynamic process and the same is clearly visible in the permittivity results. Fig. 7 shows that in the case of 0.2 and 0.6 wt% GNPs, the permittivity is enhanced at the Iso–Col_hp transition. Some theoretical and experimental results suggest that the permittivity increases at the isotropic to columnar hexagonal phase transitions in the case of homeotropic alignment.¹⁸ However, in present case the graph shows that there is no increment in the permittivity at the phase transition when sample is cooled from the isotropic phase in the case of pure HAT4 and composite having 1.2 wt% GNPs. To solve this curious problem especially for pure HAT4, we acquired data upto the 3rd cycle as well (to ensure best alignment of the molecules). But results are almost unchanged. We expect that due to the plastic (rigid) nature of the Col_hp phase of HAT4, observed values of the permittivity at 10 or 100 kHz is high frequency limiting value of the permittivity in the homeotropic configuration i.e. it represents ε^′_‖(∞). In order to get static permittivity (ε^′_‖(0)) of HAT4, one has to go at 10 or 100 Hz (ref. 53) which could not be possible here due to the conductivity effect.⁵⁴ In the case of composites having GNPs, systems are not well packed and random as well. Because of the randomness of the discs even in the Col_hp phase, permittivity values are not going below the isotropic phase values particularly for the composites having 0.2 and 0.6 wt% GNPs. But question is why it is going up instead of following the trend of the isotropic liquid phase. The fact is that in the present case, our observed values are tending towards the static value due to the possible increase of the relaxation frequency of the planar aligned molecules. Reader may note that in these two cases of Col_hp phase, there is no proper uniform alignment i.e. it has mixture of partial homeotropic and planar aligned molecules. Here it is important to mention that in the case of planar alignment of the molecules, plane of the discs are expected to be normal to the electrodes i.e. directors are normal to the measuring electric phase. In this configuration, rotation of the molecules is easier than in the homeotropic configuration and consequently high relaxation frequency is expected. Unfortunately, we are not able to determine the relaxation mechanism from the permittivity (see Fig. 8) or loss (not given) plots in the composite systems due to the high conductance even if relaxation is around 10 kHz where conductivity effects are expected to be the least. However, conductivity data (see curves 2 and 3 of Fig. 5a) show clear peaks at ∼10 kHz. Separate efforts will be needed to solve this issue. On the basis of the above discussions on the permittivity results as well, we find that alignment of the pure HAT4 and composite having 1.2 wt% GNPs is better than those in the composites having 0.2 and 0.6 wt% GNPs.

Fig. 7 Variations of the permittivity (ε′) with temperature (°C). Curve (1) for HAT4, (2) for HAT4 + 0.2 wt% GNPs, (3) for HAT4 + 0.6 wt% GNPs and (4) for HAT4 + 1.2 wt% GNPs. The vertical lines denote the extrapolated transition temperatures obtained from the DSC studies.

Fig. 8 Variations of the permittivity (ε′) with frequency. Curve (1) for HAT4, (2) for HAT4 + 0.2 wt% GNPs, (3) for HAT4 + 0.6 wt% GNPs and (4) for HAT4 + 1.2 wt% GNPs. Inset shows plots expanded view of mid region to explore any possible relaxation mechanism.

Fig. 9 shows the intensity vs. 2θ plot of SAXS for the composite (HAT4 + 1.2 wt% GNPs). Various reflections and d values obtained with them are summarized in Table 2 along with the literature data for HAT4. Observed results show that after dispersion of GNPs, the inter-columnar separation is marginally changed. The plots for the composite show the typical peaks of HAT4 with d₁₀₀ equal to 16.4 Å against the value of 16.1 Å for HAT4.^5,51,55 Other reflections are almost unchanged except that (200) reflection has reduced substantially. XRD results suggest that presence of the GNPs is not damaging the overall structure but some modification in the packing is possible as discussed here. In the hexatic packing, maximum length covered by the three molecules located on the lines joining opposite corners of the hexagon (∼3 × columns spacing) is almost equal to the diameter of GNPs (∼5 nm). Thus circle covered by molecules on hexagons is almost equal to the great circle of the GNPs. Hence, presence of GNPs will remove a cylindrical space (with axis of the cylinder parallel to the columns) having its cross sectional area equal to that of the great circle of GNPs (∼area of circle covered by molecules on hexagons) and length equal to the diameter of the GNPs. Such length will contain ∼14 layers of HAT4 molecules (GNP diameter (∼5 nm)/layer spacing of HAT4 (0.359 nm)). This arrangement will remove the interactions of the neighboring molecules with HAT4 molecules of the above 14 layers and hence average bonding strength is expected to decrease and that is why ΔH for Iso–Col_hp transition is decreasing as discussed earlier. One can note that such an arrangement is highly subtle and is possible only for low concentration of GNPs with slow cooling (as evident by various results discussed above on the bulk samples) as it will still represent minimum energy configuration. In the present case, concentration of GNPs is ∼1 to 10¹⁰ HAT4 molecules. If concentrations are high enough, packing structure is bound to collapse and the same is evident from the dwindling value of the Iso–Col_hp enthalpy/entropy with the increasing concentration of GNPs. It is also important to add that there may be some distortion of the molecular directors around GNP and columns may not be perfectly unidirectional. Due to this reason perfect dark state could not be possible in Fig 3c.

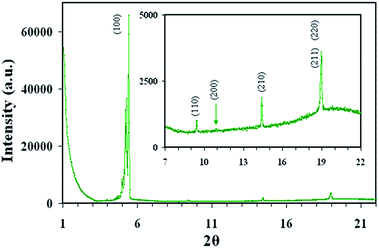Fig. 9 Intensity vs. 2θ plot for HAT4 + 1.2 wt% GNPs at 120 °C. Inset shows expanded view to show the peaks of low intensity.

Table 2 (hkl) indices, incident angle (θ) and d-spacing for the X-ray reflections in the Col_hp phase of HAT4 and its composite with GNPs

Reflection	θ in °	d spacing in Å
		HAT4 (ref. 55)	Composite
(100)	2.7	16.02	16.38
(110)	4.7	9.37	9.41
(200)	5.4	8.11	8.13
(210)	7.2	6.15	6.16
(220)	9.5	4.67	4.69
(211)	9.5	4.67	4.69
(002)	12.5	3.59	3.55
(102)	12.8	3.51	3.47

---

Fig. 9 shows that a shoulder appears at 2θ = 5.25 which gives spacing of 16.8 Å. Such shoulders appear for pure HAT4 as well and these are assigned to some kind of distortions.⁵⁵ In the case of present composite, such minor distortions may be due to the presence of GNPs. One value may be due to the undistorted structure and the other (shoulder) due to slightly distorted structure where GNPs are present. It is important to mention here that at 100 °C, we have not observed this shoulder. It is expected that if size of GNPs is increased beyond the maximum length covered by the three molecules located on the lines joining opposite corners of the hexagon, hexagonal packing may collapse because such spheres will push adjoining hexagons in the direction normal to columns' axis.

4. Conclusions

We have reported the effect of dispersion of gold nanoparticles (GNPs) of different concentrations in a discotic liquid crystal (HAT4) on the thermodynamic, optical and electrical properties. DSC studies show appreciable depreciation of the Col_hp to isotropic liquid transition temperature, enthalpy and entropy with the increasing concentration of GNPs while only minor change in the crystal to Col_hp or Col_hp to crystal transition temperatures has been observed. It has been found that the conductivity increases drastically for the higher concentration of GNPs (1.2 wt%) dispersed in HAT4 as compared to the lower concentrations (0.2 and 0.6 wt%). Dielectric relaxation frequency of the discotic molecules seems to shift towards high frequency region in the presence of GNPs. Observed results strongly supports that plastic nature of the columnar mesophase of HAT4 shows better fluidity (mesophase behavior) in the presence of small concentration (<2%) of GNPs without loosing its columnar structure (as confirmed by SAXS). However, large concentration is expected to destroy its mesomorphic nature due to increase in disorder. Surface plasmonic response has also been detected in the composite of HAT4 and GNPs. Observed results of the inorganic–organic composite system is extremely useful for many device applications such as one dimensional conductor, photovoltaic solar cell, photoconduction and light emitting diodes, etc.

Acknowledgements

The work is financially supported under a research project no. 41-857/2012 (SR) of the University Grants Commission, New Delhi. One of us (MM) thanks UGC for a fellowship under the project. Indo-Ireland international cooperation by DST, New Delhi is also acknowledged.

References

1. S. Sergeyev, W. Pisula and Y. H. Geerts, Chem. Soc. Rev., 2007, 36, 1902–1929.
2. R. J. Bushby and K. Kawata, Liq. Cryst., 2011, 38, 1415–1426.
3. S. Kumar, Liq. Cryst., 2009, 36, 607–638.
4. H. K. Bisoyi and S. Kumar, Chem. Soc. Rev., 2010, 39, 264–285.
5. E. O. Arikainen, N. Boden, R. J. Bushby, J. Clements, B. Movaghar and A. Wood, J. Mater. Chem., 1995, 5, 2161–2165.
6. S. Chandrasekhar and V. S. K. Balagurusamy, Proc. R. Soc. London, Ser. A, 2002, 458, 1783–1794.
7. S. Chandrasekhar and S. K. Prasad, Contemp. Phys., 1999, 40, 237–245.
8. Q. Zheng, G. Fang, W. Bai, N. Sun, P. Qin, X. Fan and X. Z. Zhao, Sol. Energy Mater. Sol. Cells, 2011, 95, 2200–2205.
9. L. S. Mende, A. Fechtenkotter, K. Mullen, E. Moons, R. H. Friend and J. D. Mackenzie, Science, 2001, 293, 1119–1122.
10. O. Stamatoiu, J. Mirzaei, X. Feng and T. Hegmann, Top. Curr. Chem., 2012, 318, 331–393.
11. A. Choudhary, G. Singh and A. M. Biradar, Nanoscale, 2014, 6, 7743–7756.
12. G. L. Nealon, R. Greget, C. Dominguez, Z. T. Nagy, D. Guillon, J. L. Gallani and B. Donnio, Beilstein J. Org. Chem., 2012, 8, 349–370.
13. S. Kumar, NPG Asia Mater., 2014, 6, 1–13.
14. Supreet, R. Kumar, R. Pratibha, S. Kumar and K. K. Raina, AIP Conf. Proc., 2013, 1536, 67–68.
15. Supreet, R. Pratibha, S. Kumar and K. K. Raina, Liq. Cryst., 2014, 41, 933–939.
16. S. Kumar, Liq. Cryst., 2014, 41, 353–367.
17. S. Kumar, S. K. Paul, P. Suresh and V. Lakshminarayanan, Soft Matter, 2007, 3, 896–900.
18. Supreet, S. Kumar, K. K. Raina and R. Pratibha, Liq. Cryst., 2013, 40, 228–236.
19. S. K. Prasad, K. L. Sandhya, G. G. Nair, U. S. Hiremath, C. V. Yelmaggad and S. Sampath, Liq. Cryst., 2006, 33, 1121–1125.
20. S. K. Prasad, M. V. Kumar, T. Shilpa and C. V. Yelamaggad, RSC Adv., 2014, 4, 4453–4462.
21. N. Yadav, R. Dabrowski and R. Dhar, Liq. Cryst., 2014 DOI:10.1080/02678292.2014.950619.
22. A. S. Pandey, R. Dhar, S. Kumar and R. Dabrowski, Liq. Cryst., 2011, 38, 115–120.
23. R. K. Shukla, K. K. Raina, V. Hamplova, M. Kaspar and A. Bubnov, Phase Transitions, 2011, 84, 850–857.
24. S. Tripathi, J. Prakash, A. Chandran, T. Joshi, A. Kumar, A. Dhar and A. M. Biradar, Liq. Cryst., 2013, 40, 1255–1262.
25. L. Lejcek, V. Novotna and M. Glogarova, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 012505.
26. M. Nakaya, M. Kanehara and T. Teranishi, Langmuir, 2006, 22, 3485–3487.
27. S. Sun, C. B. Murray, D. Weller, L. Folks and A. Moser, Science, 2000, 287, 1989–1992.
28. V. Novotna, J. Vejpravova, V. Hplova, J. Perokleska, E. Gorecka, D. Pociecha and M. Glogarova, RSC Adv., 2013, 3, 10919–10926.
29. U. Kreibig and M. Vollmer, Optical properties of metal clusters, Springer, Berlin, 1995.
30. M. Luis and L. Marzan, Langmuir, 2006, 22, 32–41.
31. S. Eutis and M. A. EI-Sayed, Chem. Soc. Rev., 2006, 35, 209–217.
32. W. Lewandowski, M. Wojcik and E. Gorecka, ChemPhysChem, 2014, 15, 1283–1295.
33. U. B. Singh, R. Dhar, R. Dabrowski and M. B. Pandey, Liq. Cryst., 2014, 41, 953–959.
34. K. K. Vardanyan, R. D. Walton and D. M. Bubb, Liq. Cryst., 2011, 38, 1279–1287.
35. S. Kumar and V. Lakshminarayan, Chem. Commun., 2004, 1600–1601.
36. L. A. Holt, R. J. Bushby, S. D. Evans, A. Burgess and G. Seeley, J. Appl. Phys., 2008, 103, 063712.
37. C. Kavitha, B. S. Avinash, S. Kumar and V. Laksminarayan, Mater. Chem. Phys., 2012, 133, 635–641.
38. S. Kumar, S. K. Paul and V. Lakshminarayanan, Mol. Cryst. Liq. Cryst., 2005, 434, 251.
39. H. Qi and T. Hegmann, Liq. Cryst. Today, 2011, 20, 102–114.
40. B. Glusen, A. Kettner, J. Kopitzke and J. H. Wendroff, J. Non-Cryst. Solids, 1998, 241, 113–120.
41. B. Glusen, A. Kettner and J. H. Wendroff, Mol. Cryst. Liq. Cryst., 1997, 303, 115–120.
42. R. J. Bushby, N. Boden, C. A. Kilner, O. R. Lozman, Z. Lu, Q. Liu and M. A. Thonton-Pett, J. Mater. Chem., 2003, 13, 470–474.
43. A. S. Pandey, R. Dhar, A. S. Achalkumar and C. V. Yelamaggad, Liq. Cryst., 2011, 38, 775–784.
44. A. K. Jonscher, Dielectric relaxation in solids, Chelsea, London, 1983.
45. S. L. Srivastava and R. Dhar, Radiat. Phys. Chem., 1996, 47, 287–293.
46. R. Dhar, R. S. Pandey and V. K. Agrawal, Indian J. Pure Appl. Phys., 2002, 40, 901–907.
47. J. C. Martinez, N. A. Chequer, J. L. Gonzalez and T. Cordova, J. Nanosci. Nanotechnol., 2012, 2, 184–189.
48. N. Boden, R. J. Bushby, J. Clements and R. Luo, J. Mater. Chem., 1995, 5, 1741–1748.
49. S. Marguet, D. Markovitsi, P. Millie and H. Sigal, J. Phys. Chem. B, 1998, 102, 4697–4710.
50. I. A. Levitsky, W. B. Euler, N. Tokranova and B. X. Castracane, Appl. Phys. Lett., 2004, 85, 6245–6247.
51. J. V. Keulen, T. W. Warmerdam, R. J. M. Nolte and W. Drenth, Recl. Trav. Chim. Pays-Bas, 1987, 106, 534–536.
52. P. S. Kumar, S. Kumar and V. Lakshminarayanan, J. Appl. Phys., 2009, 106, 093701.
53. P. Yaduvanshi, A. Mishra, S. Kumar and R. Dhar, Liq. Cryst. , submitted.
54. S. L. Srivastava and R. Dhar, Indian J. Pure Appl. Phys., 1991, 29, 745–751.
55. B. J. Simmerer, B. Glusen, W. Paulus, A. Kettner, P. Schuhmacher, D. Adam, K. H. Etzbach, K. Siemensmeyer, J. H. Wendroff, H. Ringsdrof and D. Haarer, Adv. Mater., 1996, 8, 815–819.

---