Kinetics and mechanism of diallyl sulfoxide pyrolysis; a combined theoretical and experimental study in the gas phase†
M. Izadyar*a and
M. R. Gholamib
aDepartment of Chemistry, Faculty of Sciences, Ferdowsi University of Mashhad, Mashhad, Iran. E-mail: izadyar@um.ac.ir; Fax: +98 5138795457; Tel: +98 5138795533
bDepartments of Chemistry, Sharif University of Technology, Tehran, Iran
First published on 14th November 2014
Abstract
A combined experimental and computational study was carried out on the gas phase pyrolysis reaction of diallylsulfoxide. Allyl alcohol and thioacrolein were detected as the major products during a unimolecular reaction. Experimental kinetic studies were carried out via a static system under the pressure of 21–55 torr and temperature of 435.2–475.1 K. Based on the experiments, the reaction is homogeneous and proceeds through a zwitterionic intermediate. Computational studies at the DFT (B3LYP) and QCISD(T) levels with 6-311++G(d,p) basis set indicated a two-step concerted pathway as the possible route. Comparison between the experimental and theoretical activation parameters for the most probable path confirmed a good agreement.
Introduction
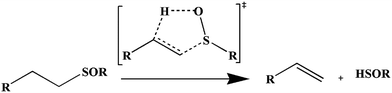
The most important mechanisms which are involved in the gas phase pyrolysis of organosulfur compounds include radical and molecular concerted pathways. The most popular concerted mechanism for the retro-ene reaction includes a six-membered transition structure (TS).1–8 Two convenient methods for direct conversion of sulfoxides to olefins are base-catalyzed β-elimination and simple pyrolysis. A yield of 90% of propene was reported by heating of diisopropyl sulfoxide and potassium-t-butoxide in dimethyl sulfoxide as solvent for 17 hours at 358 K.9 In comparison, thermal elimination requires a higher temperature but is potentially a cleaner reaction.10 These β-elimination reactions proceed through a planar, five-member cyclic transition structure and the reactions are concerted and relatively synchronous (Scheme 1).10,11During the course of this study, our attempt was focused on the case of the corresponding diallyl sulfoxide, which can formally undergo a retro-ene reaction with cyclic TS to yield propene and thioacrolein S-oxide (Scheme 2).
In contrast to the regular retro-ene reactions in the gas phase for allylic compounds, it is reported that at 438 K, pure sulfoxides smoothly decompose according to Scheme 3 with a high yield.12
In living systems, diallyl sulfoxide (DASO) is one of the main products of diallyl sulfide (DAS) oxidation in the presence of cytochrome P450 2E1 (CYP2E1).13,14 It was proved that this compound has an ability to reduce the incidence of a multitude of chemically induced tumors in the animal models. Considering this inhibitory activity of DASO for CYP2E1 increases the importance of the researches in this area. We attempted to provide further insight into the reaction kinetic using the experimental and theoretical methods. A complementary study with the aim of elucidation the molecular mechanism associated with the pyrolysis reaction is important in order to have a precise idea of the reaction pathways.
Experimental
Diallyl sulfide was synthesized and oxidized to diallyl sulfoxide according to literature.15,16 In order to increase the purity of DASO, it was kept under vacuum for several hours resulting in colorless oil. Its production was confirmed with gas chromatography (GC) and nuclear magnetic resonance (NMR) techniques. Cyclohexene was used as inhibitor for the probable free radicals during the kinetic studies and was prepared according to literature.17Product analyses were done using the gas chromatography mass spectroscopy (GC-MS) instrument (HP-5793) with a 30 m length (l), 0.25 mm inner diameter (i.d.) and HP-5 capillary column. The pyrolysis experiments were performed in a static system using a glass reaction vessel over 10 half-lives and in the presence of cyclohexene as a free radical scavenger.
Known volumes of the reactant in ethanol as internal standard was injected into the reactor using a microsyringe (HP, Agilent 5181-1267) in each kinetic run. After 10 half-lives of the reaction, the mixture was injected into the GC instrument (HP, Agilent series 6890) equipped with a flame ionization detector (FID) and a thermal conduction detector (TCD). A PS gas tight syringe was used to transfer gases into the GC capillary column (HP-5, 30 m (l) × 0.32 mm (i.d.)). The vacuum line and experimental techniques are described elsewhere.18
Computational details
Corresponding structures of the reactant, transition structures (TSs), radicals, intermediates and products were optimized, using the Gaussian 09 computational package.19 Optimized geometries of the stationary points on the potential energy surfaces (PESs) were obtained using the B3LYP20,21 functional. The 6-311++G (d,p) basis set,22 includes a set of d-type polarization functions on non-hydrogen atoms and p-type orbital on hydrogen atoms; it was applied in these calculations. The synchronous transit-guided quasi-Newton (STQN) method23 was used to locate TSs for the concerted pathways. In order to have more accurate energies for the studied radicals in the radical path, configuration interaction method (QCISD(T)) was used.24 The intrinsic reaction coordinate (IRC) method25 was also applied in order to verify the profiles connecting the TSs to two associated minima of the proposed molecular mechanisms.In order to have an estimation of the zero-point vibration energies, vibrational frequencies for all structures were calculated. This type of calculation is a useful tool to verify the nature of the stationary points as minima and TSs. In calculations of all thermodynamic and activation parameters, zero point vibrational energy and thermal corrections have been considered.
Activation parameters were also computed at 455 K. Computed activation parameters including activation energy, Ea, Arrhenius factor, A, and activation entropy, ΔS≠, have been derived from the transition structure theory (TST) according to eqn (1) and (2).26,27
| Ea = ΔH≠(T) + RT | (1) |
| A = (ekBT/h)exp(ΔS≠(T)/R) | (2) |
In these equations, R is the gas constant and is equal to 1.98 × 10−3 kcal mol−1 K−1. ΔH, T, kB and h are the activation enthalpy, the absolute temperature, Boltzmann and Plank constants, respectively.
Natural bond orbital (NBO) analysis was applied to determine the atomic charges on structures in the accepted mechanism.28,29
Results
Experimental results
In order to have more insightful knowledge of the DASO pyrolysis, it is necessary to carefully examine products and probable intermediates. GC-MS analyses showed that the major products of the reaction are ally alcohol and thioacrolein, which are shown in Scheme 3. Since propanal is a structural isomer of ally alcohol with an equal mass, it may be produced during the reaction. To reply this question, it was used their retention times (Rt) at the beginning of the study. Rt analysis confirmed only the presence of allyl alcohol.According to the stoichiometry presented in Scheme 3, this reaction requires a Pf/P0 = 2.0, where Pf is the final pressure and P0 is the initial pressure. The experimentally obtained average of 1.88 for the Pf/P0 ratio, as well as 10 half-lives for five different temperatures between 435.2 K and 475.1 K, confirmed the stoichiometry of the reaction. Table 1 demonstrates the experimental values of Pf/P0 at the reaction mean temperature. Small departure from the theoretical stoichiometry is due to the secondary reactions of thioacrolein, which causes a polymerization reaction at higher temperatures.
| T (K) | P0 | Pf | Pf/P0 | (Pf/P0) Error% | Yield% (allyl alcohol + thioacrolein) |
|---|---|---|---|---|---|
| 435.2 | 48.2 | 94.5 | 1.96 | 4.3 | 67 |
| 445.1 | 49.6 | 93.6 | 1.89 | 3.3 | 63 |
| 453.9 | 51.1 | 98.1 | 1.92 | 4.1 | 65 |
| 464.2 | 52.5 | 94.0 | 1.79 | 2.9 | 61 |
| 475.1 | 53.9 | 99.2 | 1.84 | 4.4 | 58 |
The experimental kinetic studies were done by measuring DASO decomposition percentage, using chromatographic analyses. The analysis of blank samples in the reactor, which was conducted before and after heating, showed changes in the ratio of ally alcohol to the internal standard and confirmed that the reaction takes place. An investigation of the pressure variations for ally alcohol versus time confirmed that this reaction obeys the first order rate law (Fig. S1†). According to our experiences with the vacuum system,18,30,31 four-six samples of the reaction mixture were injected into the GC at a specific time. We experimentally obtained the first order coefficients from eqn (3) in Table 2 which are independent of the initial pressure.
| k = (2.303/t)log[(P0/2P0 – Pt)] | (3) |
| T (K) | 105k (s−1) | −log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k k |
Error% |
|---|---|---|---|
| 435.2 | 1.05 | 4.98 | 3.45 |
| 445.1 | 1.95 | 4.71 | 2.33 |
| 453.9 | 5.49 | 4.26 | 4.02 |
| 464.2 | 12.6 | 3.90 | 5.16 |
| 475.1 | 23.05 | 3.64 | 2.89 |
Where t, P0 and Pt are the time, the initial pressure and the pressure at the definite time, respectively. Since molecularity of the gas phase reaction depends on the pressure, it is necessary to study the pressure effect on the reaction kinetic. For this purpose the variation of the rate coefficients with the pressure was shown in Table 3. One can see from the table that the reaction kinetic was investigated at the high pressure region of the unimolecular reaction.
| P0 (Torr) | 21 | 32 | 41 | 55 |
| 105k (s−1) | 1.07 ± 0.04 | 1.13 ± 0.09 | 1.02 ± 0.07 | 1.15 ± 0.05 |
We changed the surface to volume ratios for the reactor by 2 and 4 times greater than the unpacked reactor. Obtained rate constants for these changes are presented in Table 4. We can conclude that this reaction is homogeneous as rate coefficients are not significantly different.
| S/V (cm−1) | 105k (s−1) | Difference% |
|---|---|---|
| 1.0 | 5.49 | — |
| 2.0 | 5.22 | 4.9 |
| 4.0 | 5.61 | 2.2 |
Different ratios of cyclohexene, as radical scavenger, and DASO were injected into the vessel and products were analyzed to study the presence of possible radicals as well as the reaction mechanism. A comparison between the rate coefficients with and without cyclohexene, presented in Table 5, indicates that the reaction proceeds through a non-radical mechanism. This experimental test rejected the existence of the free radicals in experiments.
| Pcyclohexene/PDASO | 104k (s−1) | Difference% |
|---|---|---|
| 0 | 2.31 | — |
| 1.0 | 3.10 | 6.9 |
| 2.0 | 2.80 | 3.4 |
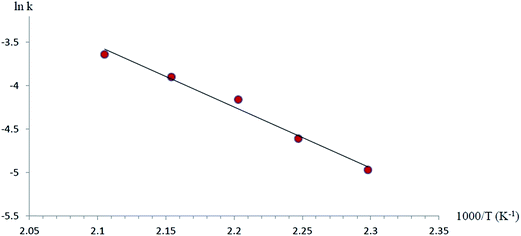
There is experimentally a linear relationship between log(2P0 – Pt) and time with approximately 87% decomposition (according to eqn (3) and Fig. S1†). After obtaining the rate constants (s−1) at different temperatures, the graphical illustration is given in Fig. 1. Considering this figure, a least square fit for the reaction is produced in the form of Arrhenius equation.
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k = (12.13 ± 0.52) − (34.1 ± 0.34) kcal/(2.303RT) k = (12.13 ± 0.52) − (34.1 ± 0.34) kcal/(2.303RT)
| (4) |
The values of activation parameters for DASO and some organosulfur sulfoxides are listed in Table 6. Activation energies, Ea, for allyl-S-allyl and Ph(CH2)3SOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 (first group) are smaller than allyl-SS-allyl ones (second group). Activation energies for DASO and Ph(CH2)3SOCH3 is almost equal and are between the upper and lower limits of listed activation energies. Different values of Ea can be interpreted by their different reaction mechanisms. For the first group that proceeds through a completely concerted mechanism, Ea is smaller than for the second group which follows a radical mechanism. A value of 34.1 ± 0.34 kcal mol−1 for the activation energy of DASO can be an evidence for the existence of a concerted mechanism. Negative value for activation entropy (−7 cal mol−1 K−1), further confirms the concerted nature of the reaction mechanism in DASO pyrolysis, too.
CH2 (first group) are smaller than allyl-SS-allyl ones (second group). Activation energies for DASO and Ph(CH2)3SOCH3 is almost equal and are between the upper and lower limits of listed activation energies. Different values of Ea can be interpreted by their different reaction mechanisms. For the first group that proceeds through a completely concerted mechanism, Ea is smaller than for the second group which follows a radical mechanism. A value of 34.1 ± 0.34 kcal mol−1 for the activation energy of DASO can be an evidence for the existence of a concerted mechanism. Negative value for activation entropy (−7 cal mol−1 K−1), further confirms the concerted nature of the reaction mechanism in DASO pyrolysis, too.
| Compound | Ea (kcal mol−1) | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A A |
−ΔS≠ (cal mol−1 K−1) | Reference |
|---|---|---|---|---|
| Allyl-S-allyl | 29.3 ± 0.1 | 10.6 ± 0.1 | 12.85 | 18 |
| Allyl-SS-allyl | 38.5 ± 0.2 | 11.9 ± 0.2 | 7.69 | 30 |
| Ph(CH2)3SOCH3 | 34.0 ± 0.4 | 12.5 ± 0.3 | 4.5 | 11 |
Ph(CH2)3SOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
30.8 ± 0.5 | 12.1 ± 0.6 | 6.5 | 11 |
| DASO | 34.1 ± 0.3 | 11.7 ± 0.3 | 7.7 | This work |
| DASO (theoretical) | 40.8 | 10.7 | 12.2 | This work |
Theoretical results
Three major mechanisms could be established for this type of pyrolysis in the gas phase. The first one is direct splitting through usual concerted TS for the retro-ene reaction which yields propene and thioacrolein S-oxide. In this mechanism, the reaction proceeds through γ-hydrogen atom transfer to an unsaturated π-bond of allyl group according to Scheme 2. However, based on the GC analysis of the reaction mixture, thioacrolein S-oxide was not detected as predicted by this mechanism. The radical mechanism starts by the homolytic cleavage of S–O bond after [2,3]-sigmatropic process according to Scheme 4 and follows by a stepwise process.As a radical pairs of CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2S˙ and ˙OCH2CH
CHCH2S˙ and ˙OCH2CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 is formed by homolysis of the reactant, S–O bond breakage is the rate determining step in the radical mechanism. This conclusion is based on the calculated relative energies (ΔE≠) for the proposed steps in Scheme 4. Calculated relative energy for the S–O homolytic dissociation is 62 kcal mol−1 which is higher than the next steps (2, 15, 22 kcal mol−1, respectively). Accordingly, S–O bond dissociation energy is the activation energy of the reaction in the radical pathway.
CH2 is formed by homolysis of the reactant, S–O bond breakage is the rate determining step in the radical mechanism. This conclusion is based on the calculated relative energies (ΔE≠) for the proposed steps in Scheme 4. Calculated relative energy for the S–O homolytic dissociation is 62 kcal mol−1 which is higher than the next steps (2, 15, 22 kcal mol−1, respectively). Accordingly, S–O bond dissociation energy is the activation energy of the reaction in the radical pathway.
After optimization of the geometry of possible radicals, shown in Scheme 4, their energies were computed at the QCISD(T) level of the theory using the 6-311++G(d,p) basis set. Computed electronic and relative energies are listed in Table S1.† Comparison of the theoretical energy barrier with the corresponding experimental value for the rate determining step (rds) (62 kcal mol−1 for the radical pathway and 34.1 ± 0.3 kcal mol−1 from the experimental data) indicates that computed barrier is higher than experiments. As the result, this mechanism is not acceptable for the reaction from the energy viewpoint. Another important parameter in mechanisms evaluation is activation entropy (ΔS≠). Calculated and experimental values of the activation entropies, +41.2 and −7.7 cal mol−1 K−1 respectively, shows that the real path should possess a concerted TS within reduction of degrees of freedom. Therefore radical and loose TS is not acceptable.
Major products in the third mechanism, ally alcohol and thioacrolein, are produced according to the reversible [2,3]-sigmatropic interconversion to alloxysulfenate as an intermediate in the first stage.32 Then a six or seven-member ring contributes in a concerted pathway as shown in Scheme 5.
Three fundamental paths were considered to investigate the concerted mechanism. These paths are defined by paths A, B, and C in Scheme 5. In the path A, after [2,3]-sigmatropic rearrangement, the pyrolysis reaction proceeds through a six-member transition structure (TS1) yielding thioacrolein (P1) and intermediate2.32 There are three paths for conversion of intermediate2 to allyl alcohol (P2). The first path is called path D in which, intermediate2 undergoes a hydrogen atom migration at the TS2, yielding allyl alcohol (P2). P1 and P3 production take places in the path E passing through the zwitterionic transition structure (TS3). This pathway is followed by P2 formation passing through the TS4. The third path, path F, is initiated by thioacrolein and methyl dioxyrane (intermediate3) formation. Then, it passes through the TS6 to produce P2.
In the second path of the proposed mechanism, path B of the concerted mechanism, pyrolysis reaction proceeds through a six-member TS (TS5) yielding thioacrolein (P1) and intermediate3. Intermediate3 can undergo a cyclic rearrangement through the four-centered transition structure (TS6) to produce P2.
TS7 is formed in path C in which P1 and P3 are produced in the first step of the proposed mechanism. This channel is followed by P2 formation passing through the TS4.
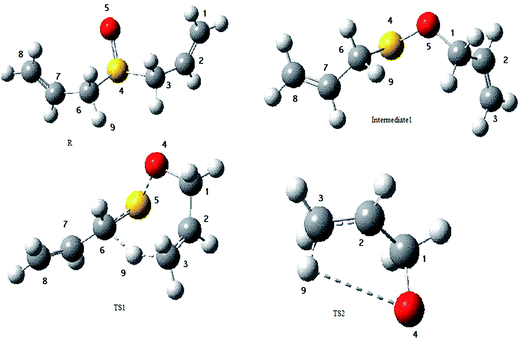
These sigmatropic rearrangements are initiated with C1–O5 bond formation and C3–S4 bond cleavage through a five-member cyclic transition structure (TS0). In this step, C1–C2 and C3–S4 bond lengths are increased, whereas C1–O5 and C2–C3 bond lengths are decreased as shown in Table 7 (for atom numbering see Fig. 2). Table 7 shows the geometrical parameters for structures involved in both molecular and ionic concerted mechanisms in path A–D.
| Parameter | DASO | Intermediate1 | TS0 | TS1 | Intermediate2 | TS2 | P1 + P2 |
|---|---|---|---|---|---|---|---|
| C1–C2 | 1.33 | 1.33 | 1.41 | 1.50 | 1.54 | 1.41 | 1.50 |
| C2–C3 | 1.49 | 1.50 | 1.23 | 1.50 | 1.54 | 1.48 | 1.33 |
| C3–S4 | 1.88 | 2.67 | 2.15 | 2.53 | — | — | — |
| C3–O5 | 3.72 | 1.44 | 2.07 | 1.19 | 1.41 | 1.42 | 1.43 |
| S4–O5 | 1.51 | 1.70 | 1.60 | 1.71 | — | — | — |
| S4–C6 | 1.88 | 1.84 | 1.88 | 1.72 | — | — | 1.64 |
| C6–H9 | 1.09 | 1.09 | 1.09 | 1.60 | 1.07 | — | — |
| C1–H9 | 4.99 | 4.99 | 4.42 | 1.28 | — | 1.35 | 1.07 |
| C1–C2–C3 | 124.03 | 124.21 | 99.24 | 121.23 | 120.0 | 115.37 | 124.23 |
| C1–H9–C6 | 88.37 | 97.52 | 87.90 | 144.97 | — | — | — |
To better understand the reaction mechanism, relative Gibbs free energies (ΔG) have been calculated and presented in Fig. 3. In Table 8, calculated Gibbs free energies in the rate determining step for all studied subroutes of the concerted pathways are reported. NBO analysis was applied to compute the natural charge changes in the rds. Table 9 shows the electrostatic charges on DASO and TS1.
| Subroutes | Steps of subroutes | ΔG≠ of rds (kcal mol−1) |
|---|---|---|
| Path A–D (purple-green lines) | Intermediate1, TS1, P1 + Intermediate2, TS2, P2 | 46.3 |
| Path A–E (purple-orange lines) | Intermediate1, TS1, P1 + Intermediate2, TS3, P1 + P3, TS4, P2 | 75.6 |
| Path A–F (purple-pink lines) | Intermediate1, TS1, P1 + Intermediate2, Intermediate3 + P1, TS6, P2 | 89.6 |
| Path B (blue line) | Intermediate1, TS5, P1 + Intermediate3, TS6, P2 | 89.6 |
| Path C (mustard line) | Intermediate1, TS7, P1 + P3, TS4, P2 | 75.6 |
| Atom | DASO | TS1 |
|---|---|---|
| C1 | −0.213 | −0.593 |
| C2 | −0.333 | −0.289 |
| C3 | −0.204 | −0.065 |
| O4 | −0.977 | −0.691 |
| S5 | 1.285 | 0.749 |
| C6 | −0.621 | −0.573 |
| H9 | 0.214 | 0.237 |
Discussion
For analyzing the concerted paths which have been shown in Scheme 5, it is useful to do a comparison between the different paths from the energy point of view. Bicyclic molecular concerted mechanism presented in path B (TS5), does not control the overall reaction due to following reasons:First, computed activation Gibbs free energies are 37.3 kcal mol−1 for TS5 and 89.6 kcal mol−1 for TS6. According to these values, it is confirmed that the second stage of this path is rds; however, its energy barrier does not correspond to the experimental value (ΔG≠ = 36.7 kcal mol−1). Second, according to the experimental and theoretical analysis, path B cannot be a competing path in the concerted mechanism, not only from the energy point of view (ΔG≠rds = 89.6 kcal mol−1, from Table 7), but also the intermediate3 was not detected in the reaction mixture.
Path C is not a good pathway for the reaction, according to the computed data, due to high activation Gibbs free energies of 41.2 and 75.6 kcal mol−1 for TS7 and TS4 (rds), respectively.
Activation Gibbs free energy for TS1, TS2, TS3, TS4 and TS6 in path A are 46.3, 44.2, 50.3, 75.6 and 89.6 kcal mol−1, respectively. Computed ΔG≠rds for the reaction paths of A–D, A–E, and A–F (Fig. 3 and Table 8) are 46.3, 75.6 and 89.6 kcal mol−1, respectively. The reaction paths following through B and C channels is possible only by activation Gibbs free energies of 89.6 and 75.6 for the corresponding rate determining steps. Comparison between the ΔG≠rds in all studied paths and experimental value of 36.7 kcal mol−1, confirms that path A followed by path D is the most feasible pathway. In this channel, it is shown that the second step is kinetically more favorable than the first one. Therefore, the first step is rds for the overall reaction.
Summarizing the mentioned notes about the all molecular and ionic channels, Fig. 3 has been presented. This potential energy diagram demonstrates the changes in the Gibbs free energies of the reaction components as a function of the reaction progress. According to this figure, the preferred paths in the concerted channel start with P1 formation, passing through the Interm1 and TS1, respectively. Then Interm2 which is a zwitterion intermediate results in P2, passing through TS2 through path D. This path (A–D with purple-green lines in Fig. 3) was described by subroutes: Intermediate1, TS1, P1 + Intermediate2, TS2, P2.
Other sources for P1 and P2 production can be considered according to Scheme S1.† 16 As can be seen from this scheme, in addition to 2-propen-1-ol, allyl propene thiosulfinate is produced in the presence of water. Experimental kinetic studies confirmed that presence of water vapors in the reaction mixture did not affect the rate coefficients at 475 K. Mass spectrometry study of the reaction mixture did not show traces of allyl propene thiosulfinate and allylSOH. Consequently, the reaction proceeding through a bimolecular mechanism was ignored.
As hydrogen transfer process plays an important role in the rds of the accepted mechanism (path A–D), high imaginary frequency for TS1 is expected. Computed value of 973.7 icm−1 for TS1 confirmed this expectation after vibrational frequencies assignment.
Looking at Table 9, it can be seen a large positive charge develops on H9 atom while C1 atom supports the electronic excess at TS1. The positive character for H9 atom allows it to be attracted by C1 atom at TS1, confirming the cyclic state of TS1 yielding zwitterionic intermediate2.
Another parameter which is insightful in selecting the proposed mechanisms and the nature of TSs is activation entropy. Computed activation entropy change during the reaction is −12.2 cal mol−1 K−1, which is in good agreement with the experimental data (−7.8 cal mol−1 K−1). Accordingly, decrease in activation entropy, confirmed the concerted nature of the reaction mechanism.
Conclusion
The kinetics and mechanism of diallyl sulfoxide pyrolysis were investigated theoretically and experimentally. The experimental studies confirmed that the pyrolysis reaction is homogeneous without the surface interferences and obeys the first order rate law. Allyl alcohol and thioacrolein were detected as major products; these products do not correspond to the retro-ene route. Several possible mechanisms were considered and the ionic path (A–D in Scheme 5) was preferred based on the theoretical and experimental results. The theoretical calculations for all transition structures and intermediates, rejected completely the concerted synchronous paths and a two-step mechanism passing through a zwitterionic intermediate was accepted. Analyses of the atomic charges showed that the initial migration of H atom and S–O bond extension can be considered as the driving force for the reaction. Relative Gibbs free energies, as a function of the reaction progress on the potential energy diagram, confirmed that the theoretical and experimental results are in agreement.Acknowledgements
The authors thank the Research Council of the Ferdowsi University of Mashhad and Sharif University of Technology for financial supporting this research.References
- J. B. Bremner and S. Samosorn, Aust. J. Chem., 2003, 56, 871 CrossRef CAS.
- C. Jin, P. Hoyoon, J. Y. Hyun, K. Sinae, J. S. Erik and L. Chulbom, J. Am. Chem. Soc., 2014, 136, 9918 CrossRef PubMed.
- H. Wu, R. N. Loeppky and R. Glaser, J. Org. Chem., 2005, 70, 6790 CrossRef CAS PubMed.
- L. J. Rodriguez, A. B. Vidal, R. E. Izquierdo, J. R. Fermin and R. Anez, THEOCHEM, 2006, 769, 211 CrossRef CAS PubMed.
- M. Izadyar and M. R. Gholami, J. Mol. Struct.: THEOCHEM, 2005, 11, 759 Search PubMed.
- M. Izadyar, A. H. Jahangir and M. R. Gholami, J. Chem. Res., 2004, 585 CrossRef CAS.
- M. Izadyar, M. R. Gholami and M. Haghgu, J. Mol. Struct.: THEOCHEM, 2004, 37, 686 Search PubMed.
- M. Izadyar and M. Zamani; Finite Elements, 1st edn, 2007, 159 Search PubMed.
- T. J. Wallace, J. E. Hofmann and A. Scheriesheim, J. Am. Chem. Soc., 1963, 85, 3406 CrossRef.
- R. D. McCulla, J. W. Cubbage and W. S. Jenks, J. Phys. Org. Chem., 2002, 15, 71 CrossRef CAS.
- J. W. Cubbage, Y. Guo, R. D. McCulla and W. S. Jenks, J. Org. Chem., 2001, 66, 8722 CrossRef CAS PubMed.
- J. W. Cubbage, Y. Guo, R. D. McCulla and W. S. Jenks, J. Org. Chem., 2001, 66, 8722 CrossRef CAS PubMed.
- S. Y. Chung, K. C. Saranjit, H. Jun-Yan and J. S. Theresa, J. Nutr., 2001, 131, 1041S Search PubMed.
- J. Pan, J. Y. Hong, E. G. Schuetz, P. S. Guzelian, W. Huang and C. S. Yang, Biochem. Pharmacol., 1993, 45, 2323 CrossRef CAS.
- I. Shwu-Chen, L. Y. Gregory, L. C. Buh, C. L. Lung and R. W. Jih, Tetrahedron, 1993, 49, 8969 CrossRef.
- E. Block and S. H. Zhao, Tetrahedron Lett., 1990, 31, 5003 CrossRef CAS.
- G. H. Coleman and H. F. John, Org. Synth., 1976, 8, 183 Search PubMed.
- M. R. Gholami and M. Izadyar, J. Phys. Org. Chem., 2003, 16, 153 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, R. E. Stratmann Jr, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Morokuma, K. Cui, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Ciolowski, J. V. Ortiz, B. B. Stefanow, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, J. L. Martin, D. J. Fox, T. Kieth, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gills, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian 09, Revision A.01, Wallingford CT, 2009 Search PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 371, 785 CrossRef.
- W. J. Hehre, L. Random, P. V. R. Schleger and J. A. Pople, Ab Initio Molecular Orbital Theory, Wiley, New York, 1986 Search PubMed.
- H. B. Schlegel, C. Peng, P. Y. Ayala and M. J. Frisch, J. Comput. Chem., 1996, 17, 49 CrossRef.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968 CrossRef CAS PubMed.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363 CrossRef CAS.
- B. Damiano and M. Fabio, Interest Rate Models - Theory and Practice, Springer, 2006 Search PubMed.
- B. Ernest; Quantum Theory of Chemical Reaction Rates, 2013 Search PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1983, 78, 4066 CrossRef CAS PubMed.
- M. R. Gholami and M. Izadyar, Chem. Phys., 2004, 301, 45 CrossRef CAS PubMed.
- M. Izadyar, N. Zamani and M. R. Gholami, Chem. Phys., 2006, 330, 394 CrossRef CAS PubMed.
- E. G. Miller, D. R. Rayner and K. Mislow, J. Am. Chem. Soc., 1966, 88, 3139 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra11403e |
| This journal is © The Royal Society of Chemistry 2014 |