Frequency response of giant electrorheological fluids in AC electric field

Abstract

It is known that in traditional dielectric electrorheological (ER) fluid the shear stress decreases or increases with the frequency of the AC electric field. However, for giant ER fluid, which is based on the principle of the polar molecule dominated electrorheological (PM-ER) effect, how shear stress varies with the frequency of the AC electric field is still not clear. In the present paper, we systematically studied the frequency dependence of PM-ER fluid by measuring the shear stresses of PM-ER fluids consisting of CTO nanoparticles under a sinusoidal electric field in a wide frequency range. It is found that the shear stress decreases with the increase of frequency when an AC electric field is applied. In PM-ER fluids there are nonuniform phase shifts appearing in shear stresses with respect to the sinusoidal electric field. These phase shifts become more pronounced as the frequency increases, which leads to the decrease of the amplitudes of the shear stresses. When the frequency is high enough, the oscillations of shear stresses smear out and the amplitudes of shear stresses reduce to a single low value. This behavior in PM-ER fluids is different from that in conventional ER fluids. For a comparison with PM-ER fluid, the response of a traditional ER fluid to frequency in an AC field is also studied, in which the particles possess high dielectric constant. The origin of different frequency responses in two types of ER fluids has been discussed and explained.

---

1. Introduction

Electrorheological (ER) fluid consists of dielectric particles and insulating liquid. The shear stress of ER fluid can be controlled by applying an electric field. For traditional (dielectric) ER effect, this behaviour is originated from the dielectric interaction of suspended particles in the electric field E, and the shear stress τ is proportional to β²E², where β is the dielectric mismatch factor.^1–5 For such ER fluids the studies on the frequency response of the shear stress in AC electric field has been reported quite a few.^6–13 It was observed that the shear stress of conventional ER fluids might decrease^6,10,13 or increase^8,9,11,12 with the frequency in an AC electric field. In most cases the shear stress of conventional ER fluids decreases with the frequency,^6,10,13 however the shear stress increases with the frequency if the particles are conductive or with high dielectric constant.^8,9,11,12 It is understood that the behaviour of frequency response for conventional ER fluids is mainly originated from the competition between the dielectric and conductive properties of particles and liquids, of which the principle was well explained.^2,7,8,12

In recent years, the researchers in the field of ER fluids focus on the giant ER fluids which is based on the principle of polar molecule dominated electrorheological (PM-ER) effect.^14–19 The yield stress of PM-ER fluids can reach more than 100 kPa under a field strength of 5 kV mm⁻¹, which is orders of magnitude higher than that of conventional ER fluids. Another character of giant ER fluids is the linear dependence of yield stress upon the electric field, rather than quadratic as for the dielectric ER fluids.^14–16 It is obvious that the PM-ER fluids are distinct from conventional ER fluids.^14–19 However it is still unknown how the PM-ER fluids behave under AC fields and what is the relation between the shear stress of PM-ER fluid and the frequency.

In this paper, by measuring the shear stresses under sinusoidal electric field at different frequencies, the frequency response of PM-ER fluids is systematically studied. The results show that the amplitude of shear stress for PM-ER fluid should decrease with increasing field frequency due to response decay. For a comparison with PM-ER fluids the response of a traditional ER fluid on frequency in AC field is also studied. As an example, this traditional ER fluid consisted of the particles with high dielectric constant shows a behaviour that the shear stress increases with the frequency. The origin of different frequency responses in two types of ER fluids has been discussed.

2. Experimental

The dielectric ER fluid was prepared by suspending BaTiO₃ particles in silicone oil. The average diameter of BaTiO₃ was ∼10 μm with a density of 6.02 g cm⁻². BaTiO₃ is a well-known dielectric material with high dielectric constant. The particles were dehydrated at 700 °C for 2 h, and then mixed with 100 cSt dry silicone oil. The suspension was ground for 1 h with an agate mortar in a dry environment. The weight percentage of the particle was 50%, corresponding to a volume fraction of 15%. The PM-ER fluid was prepared with Ca–Ti–O complex (CTO) particles suspending in hydraulic oil. The CTO particles were synthesized by co-precipitation method, during which polar molecules were adsorbed on the particle surface. The detailed synthesis process and the composition of CTO were described in previous publications.^15,16,20 The average size of CTO particles was about 50 nm, analyzed by granulometer (ZetasizerNano-ZS, Malvern Instruments Ltd, UK), and the density was 2.078 g cm⁻³ measured by a pycnometer (AccuPyc II 1340 Pycnometer, Micromeritics). The CTO particles were dried at 120 °C for 2 h and were mixed with hydraulic oil by using high-speed ball mill in agate vials for 2 h. The viscosity of hydraulic oil was about 100 mPa s, which was measured using a rheometer (Anton Parr model MCR 501). The volume fraction of CTO particles in the PM-ER fluid was 32.5%. In our experiments the silicone oil and hydraulic oil are respectively applied. In the tests we found that the giant ER behaviors are almost same by using these two oils, but the suspensions with hydraulic oil possess a better ability of anti-evaporation. The dielectric properties of silicone oil and hydraulic oil are similar and do not influence the properties of their frequency responses.

The frequency response measurements were performed with a home-made system which mainly consists of three units. (a) A concentric cylinder-cup rheometer for measuring the shear stress, in which the surfaces of electrodes were both coated with diamond grain layers to avoid sliding.²¹ The shear stresses were transferred from the recorded values of a torque sensor (0154 RW shaft end version, Dr Staiger Mohilo + CoGmbH, Germany). (b) A high voltage amplifier (Trek 10/40A), which was driven by Rigol DG1011 functional generator, supplied high voltage with slew rate ∼700 V μs⁻¹. (c) A data collection unit with sampling rate up to 4k per second was used for data collection. During the experiment, purely sinusoidal or biased sinusoidal AC fields were employed for different measurements. The sample was sufficiently stirred after each measurement to ensure in a homogeneous state. All the measurements were performed at room temperature with a fixed shear rate of 50 s⁻¹.

3. Results and discussion

(1) Frequency response of traditional dielectric ER fluid

The shear stress for traditional ER fluid with BaTiO₃ particles was measured under a sinusoid electric field of E = E₀ sin(2πft) at a shear rate of [small gamma, Greek, dot above] = 50 s⁻¹. The frequency dependence of shear stress was obtained by measuring the shear stresses with field amplitude E₀ from 0 kV mm⁻¹ to 5 kV mm⁻¹ and frequency f from 1 Hz to 1000 Hz, respectively. Fig. 1 plots a typical response curve of shear stress on E with E₀ = 5 kV mm⁻¹ and f = 100 Hz, where Fig. 1(a) is partial original curve and Fig. 1(b) is an enlarged view. Fig. 1 shows that as soon as the electric field is applied the shear stress increases to a higher value and varies with the sinusoidal field exhibiting oscillation behaviour. The minima of shear stresses correspond to E = 0 kV mm⁻¹ and the maxima correspond to E = ±5 kV mm⁻¹ respectively. The average value of shear stress is given in Fig. 1(b) with a blue solid line. It can be seen from Fig. 1(b) that there is a phase shift between shear stress and the applied sinusoidal field. The phase shift is nearly a fixed value for a certain frequency, but increases with f. The phase shift almost remains as a constant within a cycle, independent of the magnitude of the shear stress. By measuring the shear stresses of BaTiO₃ based ER fluid under sinusoidal fields with different frequencies from 1 Hz to 1000 Hz at a shear rate of [small gamma, Greek, dot above] = 50 s⁻¹, the dependences of shear stress on the field frequency can be obtained as shown in Fig. 2(a). The relationship of shear stresses and the strength of sinusoidal field with f = 100 Hz is shown in Fig. 2(b). The results indicate that the shear stress of BaTiO₃-based ER fluid is proportional to E₀², reflecting the typical characteristic of dielectric ER fluid. Fig. 2(c) shows the relation of shear stress and shear rate under sinusoidal field of E₀ = 5 kV mm⁻¹ and f = 100 Hz. In all figures, maximum and minimum amplitudes of shear stresses respectively correspond to |E| = 5 kV mm⁻¹ and E = 0 kV mm⁻¹ of the sinusoidal fields. It is noticed that the magnitude of shear stress does not drop down to zero at E = 0 kV mm⁻¹ when f is not very low. This indicates that the shear stress of traditional ER fluid consisted of BaTiO₃ particles in a sinusoidal field monotonically increases with increasing frequency. The origin of this phenomenon comes from the dielectric contribution of mismatch factor β² as described before.¹² Anyhow, the shear stress of such type ER fluid is low, usually less than 1 kPa.

Fig. 1 The shear stress response on sinusoid electric field for BaTiO₃ based traditional ER fluid. (a) The shear stress (blue) vs. sinusoidal field E = E₀ sin(2πft) (red) of f = 100 Hz at shear rate of [small gamma, Greek, dot above] = 50 s⁻¹, (b) an enlarged view of shear stress vs. sinusoidal field, and the blue straight line indicates the average value of shear stress.

Fig. 2 Dependences of shear stress on field frequency, field strength and shear rate for BaTiO₃ based traditional ER fluid. (a) Shear stress vs. frequency of sinusoidal field E = E₀ sin(2πft) with E₀ = 5 kV mm⁻¹ at shear rate 50 s⁻¹ for f = 0 Hz to f = 1000 Hz. (b) The shear stress varying with the strength of sinusoidal field of E₀ = 0–5 kV mm⁻¹ and f = 100 Hz at shear rate 50 s⁻¹. (c) The relation of shear stress and shear rate under sinusoidal field of E₀ = 5 kV mm⁻¹ and f = 100 Hz, in which the orange solid circles present zero field shear stress. In all figures the blue square dots are the averaged shear stress, the red and dark dashed lines are the minimum and maximum values respectively.

(2) Frequency response of PM-ER fluid

The shear stress of PM-ER fluid is much higher than that of traditional ER fluid and the principles of them are distinctly different.^11–18 The frequency dependence of PM-ER fluid in an AC field should also be different from that of traditional one. We measured the frequency response of the shear stresses of PM-ER fluids under both unbiased and biased sinusoidal electric field at a fixed shear rate of [small gamma, Greek, dot above] = 50 s⁻¹.

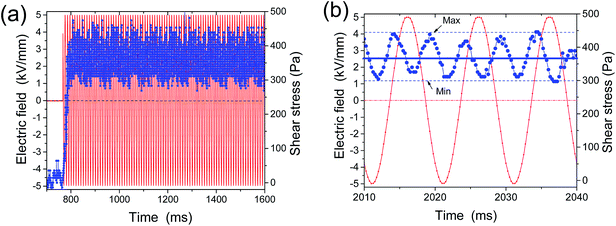
When a unbiased sinusoidal electric field E = E₀ sin(2πft) with E₀ = 4 kV mm⁻¹ is applied at different frequencies ranged from f = 1 Hz to 100 Hz, the response curves of shear stress on E can be obtained for each specified frequency. Some selected response curves of shear stress vs. E = E₀ sin(2πft) at f = 1 Hz, 10 Hz, 50 Hz and 100 Hz and at shear rate of 50 s⁻¹ are shown in Fig. 3. It can be seen that the behaviors of shear stress varying with E in the regions of 0–π and π–2π are same, due to the equal response of shear stress in both positive and negative electric field. However the maximum magnitude of shear stress at low frequency is large and decreases with increased frequency. It is clear in Fig. 3 that the maximum magnitude of shear stress can reach up to about 20 kPa in a field of f = 1 Hz, while the induced oscillation causes the shear stress almost being smeared out to about 5 kPa in same field E with f = 100 Hz. This will be clearly demonstrated in an inset of Fig. 5(b) presented later on, which shows the maximum and minimum values of shear stress in a region of f from 1 Hz to 100 Hz. This phenomenon is due to the response decay of shear stress on E in PM-ER fluids. Obviously there are phase shifts for the shear stress corresponding to E and the shifts augment gradually as the frequency increases. Therefore, the shear stress in a sinusoidal electric field can be expressed as τ(E) = τ_m(E₀) sin[2πft + δ(f,t)] + τ₀(f), where τ_m(E₀) and δ(f,t) are the amplitude of shear stress and phase shift respectively, τ₀(f) is residual stress. δ(f,t) is not a constant for a fixed frequency in a period from 0 to 2π and τ₀(f) is a function of frequency.

Fig. 3 Selected curves of shear stress (blue) varying with sinusoidal electric field E = E₀ sin(2πft) (red) of (a) f = 1 Hz, (b) f = 10 Hz, (c) f = 50 Hz and (d) f = 100 Hz and at shear rate of 50 s⁻¹ for CTO based PM-ER fluid.

In order to give a distinct picture, the response of shear stress in a sinusoidal electric field with bias E_b is carefully studied in a wide frequency range of f = 0.5–1000 Hz. Using a biased sinusoidal electric field E = E₀ sin(2πft) + E_b, an advantage is only one maximum of shear stress in the period from −π to π as E changing from 0 kV mm⁻¹ to E₀ + E_b. The dependences of magnitude and phase shift of shear stress on frequency of electric field are intuitional in this configuration.

Fig. 4 shows how the shear stresses of PM-ER fluids respond to a field of E = E₀ sin(2πft) + E_b for f = 0.5 Hz, 15 Hz, 50 Hz and 100 Hz, where E₀ = 2 kV mm⁻¹ and E_b = 2 kV mm⁻¹. The relations of shear stress vs. time and shear stress vs. E are illustrated in left and right columns of Fig. 4, respectively. When the frequency is low, f = 0.5 Hz for instance, the shear stress varies sinusoidally with quite large amplitudes from 2 kPa to 20 kPa as shown in Fig. 4(a)-1. However, there are some slight time delays of shear stress τ(E) comparing to the field E and hence an asynchronism in the relation of τ(E) and E in Fig. 4(a)-2 appears. Obviously there is an uneven phase shift on shear stress in a period of sine wave. When the frequency of the field is high, the shear stress tends to a constant value and their wave patterns vary no longer with any sinusoidal shape. From all measured curves of τ(E) = τ_m sin[2πft + δ(f,t)] + τ₀(f) in the field of E = (2 kV mm⁻¹)sin(2πft) + (2 kV mm⁻¹) from f = 0.5 Hz to f = 1000 Hz, the phase shifts and the amplitudes of shear stresses varying with frequencies are drawn in Fig. 5(a) and (b) respectively. Fig. 5(a) shows the phase shifts of τ(E) for some selected frequencies in a cycle from −π to π. It can be seen that the phase shift δ(f,t) is small at low frequency and increases with f. Furthermore, for a fixed f, δ(t) is not a constant in the period from −π to π. For instance, in the case of f = 0.5 Hz, δ ≈ 0.16π at −π/2 and δ ≈ 0.03π at π/2. As f ≥ 100 Hz, the phase shift δ even reaches up to π with nonuniform variation in the cycle from −π to π. Such large and nonuniform phase shift must smear out the amplitude variation of shear stress in sinusoidal field and thus cause τ(E) approaching a stable value around 5 kPa. A Fourier transform of τ(E) function for f = 100 Hz, as shown in the upper right inset of Fig. 4(d)-2, demonstrates that there are many frequency components contained in τ(E), which makes the amplitude of τ(E) reduced.

Fig. 4 The electric field (red) and shear stress (blue) vs. time (left column), the shear stress vs. electric field (right column) at 0.5 Hz (a), 15 Hz (b), 50 Hz (c), 100 Hz (d) under E = (2 kV mm⁻¹)sin(2πft) + 2 kV mm⁻¹ field and at shear rate of 50 s⁻¹. The insets are the drawings of partial enlargement. In plot of (d)-2, the upper right inset demonstrates the Fourier transform of shear stress for f = 100 Hz.

Fig. 5 The effect of frequency on phase shift and amplitude of shear stress for PM-ER fluid under E = (2 kV mm⁻¹)sin(2πft) + 2 kV mm⁻¹ field at shear rate of 50 s⁻¹. (a) The phase shift of shear stress in the period of −π and π for some selected frequencies. (b) The amplitudes of shear stress vary with the frequency, of which the inset is the shear stress decreases with frequency increasing in the case of unbiased sinusoid field.

(3) The origin of the difference between traditional ER fluids and PM-ER fluids

It has been demonstrated that in an AC field the frequency responses of the shear stress for traditional ER fluids and PM-ER fluids are fundamentally different. The shear stress of traditional ER fluids can increase with the frequency of AC field for the ER fluids consisted of the particles with high dielectric constant, while that of PM-ER fluids always decreases when the frequency increases.

As described above the traditional ER effect is derived from the particle polarization, in which the mismatch factor β plays a crucial role. In the polarization process the polarizing time is fast enough to response the change of AC field in frequency range to 10³ Hz. Thus β² increases with increased frequency and can enhance the attractive forces between particles in the ER fluid consisted of the particles with high dielectric constant, i.e. the shear stress increases monotonically. Although the shear stress of such type ER fluid is low, the enhancement factor can be as large as a factor of 10² from a DC field to an AC field of 10³ Hz, correspondingly the shear stress increases from few Pascal to hundreds of Pascal.

On the other hand, the polar molecules adsorbed on the particles dominate the PM-ER effect.^14–16 When an electric field E is applied and then the particles will attract each other to form chains through the dielectric interaction as the traditional ER effect. In the gap between the particles the local electric field E_loc can be more than 10² times higher than E. Under a strong local electric field E_loc between particles, polar molecules are able to be orientated along the field direction and interact with the polarized charges on particles. Such interaction is 2–3 orders of magnitude stronger than that of polarized particles as in conventional ER fluids. So that the shear stress of PM-ER fluids can reach hundreds of kPa.

The adsorption energy U_ad of the polar molecules on the particles is nearly KT, where K is Boltzmann constant and T is absolute temperature. As long as the interaction energy μE_loc of E_loc and polar moment μ is larger than KT the polar molecules adsorbed on the particles can turn their directions. If the amplitude of E is smaller than a certain value in the period of applied sinusoidal field E = E₀ sin(2πft), the E_loc will be not large enough to satisfy the condition of μE_loc > KT. The polar molecules adsorbed on the particles are unable to turn to the direction of electric field. Thus only the amplitude of sinusoidal field is higher and causes μE_loc > KT, the polar molecules can be turned to the direction of electric field and result in the PM-ER effect. As E in a period of sinusoidal field is reduced to a value corresponding to E_loc < KT, the polar molecules will turn back to original adsorption configuration on the surface of particles, and then the PM-ER effect disappear. Fig. 6 illustrates how the adsorbed polar molecules affect in an AC field. The gray area of a sinusoidal field in Fig. 6(a) indicates the corresponding region of μ|E_loc| < KT where the adsorbed polar molecules are unable to responding the field as shown in Fig. 6(c). If μE_loc > KT in the range of 0 to π or μ|−E_loc| > KT in π to 2π, the adsorbed polar molecules are able to turn their orientation as shown in Fig. 6(d) and (e) respectively, and then correspondingly the shear stress caused by PM-ER effect emerges. All these procedures must create a time delay of shear stress responding to the AC field. On the other hand the local electric field E_loc in between the particles is related to the particle size. The amplitudes of local field E_loc for various particles are different in a same applied field because of the unequal particle size in the suspension. Assuming the gap widths between particles are the same, the larger particles will induce larger E_loc. It means that in a E = E₀ sin(2πft) field the local field E_loc are different for the particles with different size. Hence the gray area shown in Fig. 6(a) will vary with the sizes of the particles due to E_loc is related with the size of particle. Therefore in PM-ER fluids, turning and returning the orientations of polar molecules in an AC electric field cannot well follow the variation of the field and cause a complex phase shift. The behaviour is about the same by using an unbiased or biased sinusoidal field as shown in Fig. 5(b).

Fig. 6 (a) In a sinusoidal field the gray area corresponds to the region of μE_loc < KT in the range of 0 to π and μ|−E_loc| < KT in π to 2π. (b) The original configuration of the polar molecules adsorbed on the particles as E = 0 or μ|E_loc| < KT. (c) The configuration of the polar molecules on the particles as μE_loc < KT in the range of 0 to π. (d) and (e) Present the configurations of the polar molecules on the particles as μE_loc > KT in the range of 0 to π and μ|−E_loc| > KT in the range of π to 2π respectively. The polar molecule will turn to the direction of E_loc and interact with the polarization charges on the particles. Here we assume only one polar molecule (green color) plays role.

As described above the PM-ER effect cannot occur in the region of μ|E_loc| < KT and E_loc is related with the size of particles. This factor is also able to be employed to explain the phenomena usually observed that the shear stress of PM-ER fluids rises very gently in the region of low DC field strength. Because of the unequal size distribution of particles, the particles with larger size need lower field strength and that with small size need higher field strength for getting same E_loc. Therefore the number of responding particles gradually increases as the field strength increases. Once the strength of the applied field is high enough, all particles can contribute to PM-ER effect and then the shear stress increases linearly with field strength increasing.

The measured response time for PM-ER fluids is about 10 ms, which is longer at the rising edges of shear stress and shorter for its falling edges.²² The patterns of shear stress of PM-ER fluids shown in Fig. 5 indicate that the phase shift is larger in the first half cycle of −π to 0 in the case of using a sinusoidal field with bias. This means that the response delay on shear stress is longer in the rising region of the sinusoidal field. When frequency is enough high, i.e. f ≥ 100 Hz for our measured samples, the response delay spreads unequally in a cycle and phase shift can even reach to π. Therefore the amplitudes of shear stress of PM-ER fluids decrease with frequency increasing in an AC field. The dependence of response time on the volume fraction and electric field strength in an AC field will be presented elsewhere.²² The tendency of shear stress of PM-ER fluids decreasing with frequency increasing remains the same. Although based on the traditional ER effect at times the polarization force of particles can have a positive effect on the shear stress from increasing frequency as shown in Fig. 2(a), however the contributed values are as small as 10² Pa and can be neglected.

4. Summary and conclusions

The dependence of shear stress of PM-ER fluids consisted of CTO nano-particles on the frequency of sinusoidal electric field has been systematically studied in a wide frequency range. For a comparison, the frequency response of shear stress for traditional ER fluids consisted BaTiO₃ particles is also measured. It is found that the amplitude of shear stress for PM-ER fluids decreases with the increase of AC field frequency. This behavior is in strong contrast to traditional ER fluid. For a traditional ER fluid consisted of particles with high dielectric constant the shear stress is enhanced by increasing frequency. The behavior in traditional ER fluids is due to the dielectric mismatch of particles and fluid, and also the dominating role of high dielectric constant of particles. However, the origin of PM-ER effect is based on the orientation of polar molecules in between particles, this orientation causes a time delay on responding shear stress. The shear stress of PM-ER fluid cannot well follow the change of field and a nonuniform phase shift exists, which deduces the amplitude of responding shear stress. Thus the amplitude of shear stress for PM-ER fluids decreases with increasing frequency of AC field. As frequency of AC field is low, the shear stress closely follows the sinusoidal shape with clearly identifiable maximum and minimum values, while the amplitude of shear stress reduces to a single value when the frequency is high enough. The phenomena can be well explained using the mechanism of PM-ER effect. This result provides a new knowledge to understand the behavior of PM-ER fluid and must be beneficial for its applications.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant no 10674156 and 11174332), and the Instrument Developing Project of the Chinese Academy of Sciences (Grant no. YZ200758).

References

1. R. Tao and J. M. Sun, Phys. Rev. Lett., 1991, 67, 398–401.
2. H. R. Ma, W. W. Wen, W. Y. Tam and P. Sheng, Phys. Rev. Lett., 1996, 77, 2499–2502.
3. L. C. Davis, J. Appl. Phys., 1997, 81, 1985–1991.
4. R. Tao, Q. Jiang and H. K. Sim, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 2727–2735.
5. P. Sheng and W. Wen, Solid State Commun., 2010, 150, 1023–1039.
6. L. C. Klass and T. W. Martinek, J. Appl. Phys., 1967, 38, 67–74.
7. L. C. Davis, J. Appl. Phys., 1992, 72, 1334–1340.
8. L. C. Davis, J. Appl. Phys., 1993, 73, 680–683.
9. A. Inoue, Proceedings of the 2nd International Conference on Electrorheological Fluids, ed. J. D. Carlson, A. F. Sprecher and H. Conrad, Technomic, Lancaster-Base, 1990, p. 176.
10. T. Y. Chen and P. F. Luckham, Colloids Surf., A, 1993, 78, 167–175.
11. W. J. Wen and K. Q. Lu, Appl. Phys. Lett., 1995, 67, 2147–2148.
12. K. Q. Lu, W. J. Wen, C. X. Li and S. S. Xie, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 6329–6332.
13. C. W. Wu, Y. Chen and H. Conrad, J. Phys. D: Appl. Phys., 1998, 31, 960–963.
14. W. Wen, X. Huang, S. Yang, K. Lu and P. Sheng, Nat. Mater., 2003, 2, 727–730.
15. K. Q. Lu, R. Shen, X. Z. Wang, G. Sun, W. J. Wen and J. X. Liu, Chin. Phys., 2006, 15, 2476–2480.
16. R. Shen, X. Z. Wang, Y. Lu, D. Wang, G. Sun, Z. X. Cao and K. Q. Lu, Adv. Mater., 2009, 21, 4631–4635.
17. P. Tan, W. J. Tian, L. W. Zhou and J. P. Huang, J. Phys. Chem. B, 2009, 113, 5412–5417.
18. C. S. Orellana, J. B. He and H. M. Jaeger, Soft Matter, 2011, 7, 8023–8029.
19. Y. D. Liu and H. J. Choi, Soft Matter, 2012, 8, 11961–11978.
20. S. H. Yang, X. Gao, C. X. Li, Q. Wang, R. Shen, G. Sun and K. Q. Lu, Mod. Phys. Lett. B, 2012, 26, 1150023.
21. X. Z. Wang, R. Shen, D. Wang, Y. Lu and K. Q. Lu, Mater. Des., 2009, 30, 4521–4524.
22. R. Shen, R. Liu, D. Wang, G. Sun, K. Chen and K. Q. Lu, The dynamic response and relaxation of giant electrorheological fluids, to be published.

---