Understanding the selectivity in the formation of δ-lactams vs. β-lactams in the Staudinger reactions of chloro-cyan-ketene with unsaturated imines. A DFT study

Abstract

The reactions of chloro-cyan-ketene with two phenyl substituted unsaturated imines yielding β- or δ-lactams have been investigated using DFT methods at the MPWB1K/6-311G(d,p) level in diethyl ether. The reactions are initialised by the nucleophilic attack of the unsaturated imines on the ketene with formation of zwitterionic intermediates. The subsequent C–C single bond formation at the imine carbon or at the β-conjugated position enables the formation of β- or δ-lactams. Analysis of the energies involved in the two competitive channels explains the selectivity experimentally observed; in the absence of any steric hindrance, formation of δ-lactams is favoured over the formation of β-lactams. ELF topological analysis allows explaining the bonding changes along the two competitive channels. While formation of the N–C bond takes place by participation of the nitrogen lone pair, formation of the C–C bonds takes place through a retrodonation process involving the C–C double bond of the ketene and the C–N or C–C double bonds of the unsaturated imine. ELF topological analysis makes it possible to rule out an electrocyclic mechanism for the cyclisation step.

---

Introduction

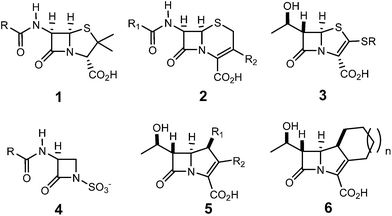
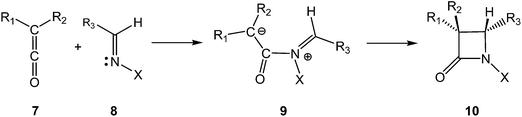
The β-lactam skeleton is the key structural element of the most widely employed family of antimicrobial agents to date, β-lactam antibiotics, which include as representative structural classes (Scheme 1) penams 1, cephems 2, penems 3, monobactams 4, carbapenems 5, and trinems 6, among others.¹

Scheme 1 Some representative structural classes of β-lactam antibiotics.

The first classical synthesis of molecules containing the β-lactam skeleton was the Staudinger reaction,² which is a formal [2 + 2] cycloaddition between a ketene 7 and an imine 8 (Scheme 2).^3–5 Mechanistic studies revealed that two key steps are involved in the β-lactam formation: (i) the nucleophilic attack of an imine 8 on a ketene 7 to generate a zwitterionic (ZW) intermediate 9; (ii) the cyclisation of the ZW intermediate 9 to yield β-lactam 10.³ In addition to the reaction mechanism, the diastereoselectivity of the Staudinger reaction has been an intensive research area for several decades.⁶

Scheme 2 Mechanism of the Staudinger reaction.

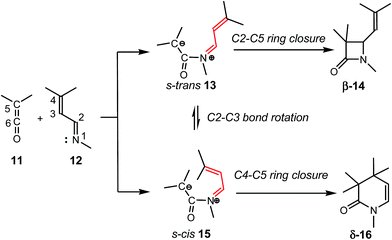
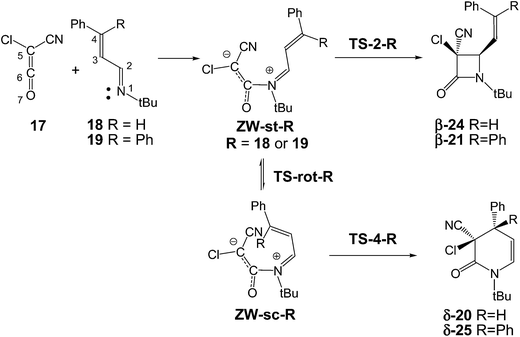
The reaction of ketenes 11 and α,β-unsaturated imines (UIs) 12 can yield either β-lactams β-14 or δ-lactams δ-16 (Scheme 3).⁵ While β-lactams β-14, the formal [2 + 2] cycloadducts (CAs) of Staudinger reactions, originate from of the C2–C5 ring closure in s-trans ZW intermediates 15, δ-lactams δ-16, the formal [2 + 4] CAs of aza-Diels–Alder (ADA) reactions, originate from the C4–C5 ring closure in s-cis ZW intermediates 15. Conformational s-trans and s-cis ZW intermediates 13 and 15 resulting from the nucleophilic attack of UIs 12 on ketenes 11 may equilibrate via a C2–C3 single bond rotation,⁷ thus connecting both competitive channels. Therefore, the energy associated with this C2–C3 bond rotation, and the energies associated with the cyclisation steps at the corresponding ZW intermediates may determine the formation of a β-lactam β-14 vs. a δ-lactam δ-16.

Scheme 3 Reactions between ketenes 11 and α,β-unsaturated imines 12.

The selectivity in the formation of β-lactams vs. δ-lactams was experimentally studied first by Moore⁸ and then by Brady⁹ in the reactions of chloro-cyan-ketene (CCK) 17 with the phenyl substituted UIs 18 and 19. Interestingly, when the diphenyl substituted UI 19 (R = Ph) was used, the expected β-lactam β-21, coming from the Staudinger reaction, was exclusively obtained, but when the phenyl substituted UI 18 (R = H) was used, the δ-lactam δ-20, the product of the ADA reaction, was obtained as the only product (see Scheme 4). Both reactions were completely cis/trans selective, i.e. while the cyano and phenyl substituent in δ-lactam δ-20 presented a cis relation, the cyano and vinyl substituent in β-lactam β-21 presented a trans relation.^8,9

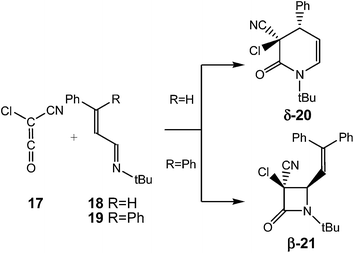Scheme 4 Experimental reaction of CCK 17 with UIs 18 and 19.^8,9

A plethora of theoretical studies has been devoted to establish the mechanism of the Staudinger reaction, as well as the stereoselectivity in the cyclisation step.¹⁰ The accepted mechanism of the Staudinger reaction is shown in Scheme 2. The reaction begins with the nucleophilic attack of imine 8 on the carbonyl C6 carbon of ketene 7 to yield ZW intermediate 9. The subsequent ring closure at this intermediate yields β-lactam 10. This step has been associated with an electrocyclic reaction.^5,10d Consequently, a conrotatory electrocyclisation process at the zwitterionic intermediate 9 was proposed along the formation of β-lactams. Although the ring closure mechanism differs in nature from that for the electrocyclic ring closure of 1,3-butadiene, Cossío has suggested that the strong analogy in the so-called torquoselectivity¹¹ of these reactions when it was compared to the pericyclic reactivity of 1,3-butadienes supported the assumption of the pericyclic reactivity of the zwitterionic intermediate 9.^5,10b

The analysis of the electron density reorganisation to evidence the bonding changes along a reaction path is the most attractive method to characterise a reaction mechanism.^12,13 An appealing procedure that provides a straightforward connection between the electron density distribution and the chemical structure is the study of the quantum chemical topology of the electron density based on the electron localisation function (ELF) of Becke and Edgecombe.¹⁴ In this sense, Silvi and Savin presented the ELF in a very chemical fashion, using their topological analysis as an appealing chemical bonding model.¹⁵ In this field, Andrés performed a systematic investigation characterising the mechanisms of significant organic reactions.¹⁶

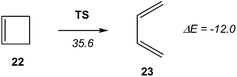
Recently, Andrés performed an ELF quantum topological analysis along the intrinsic reaction coordinate¹⁷ (IRC) curve associated with the ring aperture of cyclobutene 22 yielding 1,3-butadiene 25 (see Scheme 5).¹³

Scheme 5 Electrocyclic aperture of cyclobutene 22. Energies are in kcal mol⁻¹.

ELF topological analysis revealed that the bonding changes take place along five differentiated stages (see Scheme 6).¹³ Some appealing conclusions were obtained from this ELF topological analysis: (i) the ring aperture process begins in the stage I by the homolytic C3–C4 bond rupture to form a pseudodiradical species A; (ii) on going to the transition state (TS) of the reaction along stage II, the C1–C2 double bond present in cyclobutene 22 is also broken. Thus, the rupture of the C3–C4 single bond and the C1–C2 double bond accounts for the high activation energy demanded to reach the TS of the reaction, 35.6 kcal mol⁻¹; (iii) the sequential bonding changes found along the one-step mechanism indicate that the reaction is non-concerted. This behaviour makes it possible to strongly reject the proposed pericyclic mechanism¹⁸ for the ring closure of 1,3-butadiene 23;¹⁹ and (iv) as the ring aperture begins with the rupture of the C3–C4 single bond, the molecular orbital (MO) symmetry analysis based on the p_z atomic orbital of butadiene should be rejected to explain the conrotatory aperture.²⁰ Steric hindrance of the closest substituents present at the C3 and C4 carbons associated with a disrotatory aperture could explain the stereoselectivity of the reaction.

Scheme 6 Schematic representation of the five stages of the one-step mechanism associated with the ring aperture of cyclobutene 22.

Although a considerable amount of theoretical work has been dedicated to the study of the stereoselectivity in the formation of β-lactams, few studies have analysed the selectivity in the formation of β-lactams vs. δ-lactams, being mainly based on MO interactions.^7,21 The selectivity in the formation of β-lactams vs. δ-lactams in the Staudinger reaction involving UIs has been categorised as periselectivity.²² The IUPAC Gold Book²³ defines the periselectivity as “the differentiation between two symmetry-allowed processes, for example the [2 + 4] vs. [4 + 6] cycloaddition of cyclopentadiene to tropone”. However, neither the formal [2 + 2] cycloaddition involved in the Staudinger reactions nor polar DA reactions²⁴ are pericyclic reactions, and in consequence, the selectivity in the formation of β-lactams vs. δ-lactams should not be categorised as periselectivity.

Herein, the reactions of CCK 17 with the phenyl substituted UIs 18 and 19 yielding lactams δ-20 or β-21 are investigated using DFT methods at the MPWB1K/6-311G(d,p) computational level in diethyl ether (DEE) (see Scheme 4).^8,9 An energy and geometrical analysis of the stationary points, TSs and ZW intermediates, involved in the endo competitive channels allowing the formation of lactams δ-20 or β-21 is performed in order to explain the selectivity in the formation of δ-lactams vs. β-lactams. Finally, an ELF topological analysis along the competitive channels associated with the reactions of CCK 15 with UI 16 is performed in order to characterise the molecular mechanisms involved in the formation of β- and δ-lactams.

Computational methods

DFT computations were carried out using the MPWB1K²⁵ exchange-correlation functional, together with the standard 6-311G(d,p) basis set.²⁶ The optimisations were performed using the Berny analytical gradient optimisation method.²⁷ The stationary points were characterised by frequency computations in order to verify that TSs have one and only one imaginary frequency. The IRC paths¹⁷ were traced in order to check the energy profiles connecting each TS to the two associated minima of the proposed mechanism using the second order González-Schlegel integration method.²⁸ Solvent effects of DEE in the optimisations were taken into account using the polarisable continuum model (PCM) as developed by Tomasi's group²⁹ in the framework of the self-consistent reaction field (SCRF).³⁰ Values of enthalpies, entropies and free energies in DEE were calculated with the standard statistical thermodynamics at 25.0 °C and 1 atm.²⁶ The “int = ultrafine” Gaussian keyword was used in the DFT integrations. The electronic structures of stationary points were analysed by the natural bond orbital (NBO) method³¹ and by the ELF topological analysis, η(r).¹⁴ The ELF study was performed with the TopMod program³² using the corresponding monodeterminantal wavefunctions of the selected structures of the IRC. All computations were carried out with the Gaussian 09 suite of programs.³³

The global electrophilicity index,³⁴ ω, is given by the following expression, ω = (μ²/2η), in terms of the electronic chemical potential μ and the chemical hardness η. Both quantities may be approached in terms of the one-electron energies of the frontier molecular orbital HOMO and LUMO, ε_H and ε_L, as μ ≈ (ε_H + ε_L)/2 and η ≈ (ε_H + ε_L), respectively.³⁵ The global nucleophilicity index,³⁶ N, based on the HOMO energies obtained within the Kohn–Sham scheme,³⁷ is defined as N = E_HOMO(Nu) − E_HOMO(TCE). This relative nucleophilicity index is referred to tetracyanoethylene (TCE). The global reactivity indices of the reagents computed at the MPWB1K/6-31G(d) level are given in the ESI.†

Results and discussion

The present theoretical study has been divided into two parts: (i) first, energy and geometry details of the formation of lactams δ-20 and β-21 in the reactions of CCK 17 with UIs 18 and 19 are given; (ii) then, an ELF topological analysis of the two competitive channels associated with the stepwise reaction between CCK 17 and UI 18 yielding lactams β-24 and δ-20 is carried out in order to characterise the molecular mechanisms.

(i) Energy and geometry details of the formation of lactams δ-20 and β-21 in the reactions of CCK 17 with UIs 18 and 19

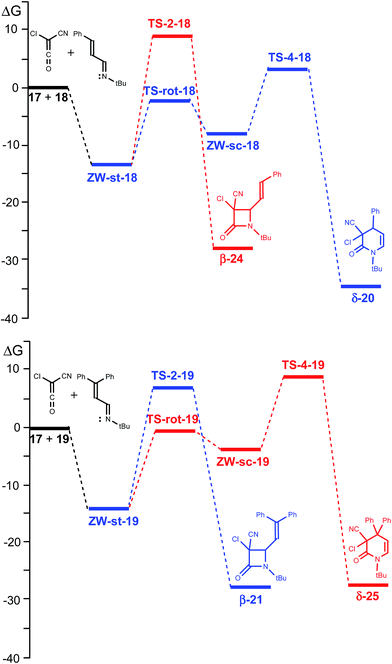
The reactions between CCK 17 and phenyl substituted UIs 18 and 19 to yield β-lactams β-24 and β-21, the products of Staudinger reactions, or δ-lactams δ-20 and δ-25, the products of ADA reactions, present stepwise mechanisms through the formation of ZW intermediates (see Scheme 7). An analysis of the reaction path associated with the nucleophilic attacks of UIs 18 and 19 on the carbonyl carbon of CCK 17 indicates that they do not present any appreciable activation energy, yielding directly the ZW intermediates without any TSs. Consequently, only the ZW intermediates, ZW-st-R and ZW-sc-R (R = 18 or 19), and the TSs associated with the ring closures, TS-2-R and TS-4-R, were located and characterised (see Scheme 7). Relative enthalpies, entropies and free energies are given in Table 1. Total enthalpies, entropies and free energies are given in the ESI.†

Scheme 7 Mechanisms of the reactions of CCK 17 with UIs 18 and 19.

Table 1 MPWB1K/6-311G(d,p) relative^a enthalpies (ΔH, in kcal mol⁻¹), entropies (ΔS, in cal mol⁻¹ K⁻¹) and free energies (ΔG, in kcal mol⁻¹), computed at 25.0 °C and 1 atm in DEE, of the stationary structures involved in the reactions of CCK 15 with UIs 18 and 19

	ΔH	ΔS	ΔG
a Relative to 17 + 18 or 17 + 19.
ZW-st-18	−25.6	−40.8	−13.4
TS-rot-18	−15.0	−41.9	−2.5
ZW-sc-18	−20.6	−42.1	−8.0
TS-2-18	−4.4	−43.9	8.7
TS-4-18	−11.4	−49.0	3.2
β-24	−40.6	−41.4	−28.2
δ-20	−50.0	−51.1	−34.7
ZW-st-19	−28.6	−50.2	−13.7
TS-rot-19	−17.3	−58.2	−1.0
ZW-st-19	−20.7	−57.8	−3.4
TS-2-19	−9.6	−55.7	7.0
TS-4-19	−8.7	−59.9	9.2
β-21	−42.4	−49.2	−27.8
δ-25	−45.3	−61.5	−27.0

---

Due to the asymmetry of CCK 17, two stereoisomeric approach modes are feasible along the nucleophilic attacks; the endo and the exo ones.^10b Along the endo channels, the cyano group of CCK 17 is placed over the sp² hybridised imine N1 nitrogen of these UIs. The ZW intermediates resulting from the endo approach mode are 2.1 kcal mol⁻¹ more stable than the exo ones. Moore⁸ and Brady⁹ suggested that the endo/exo selectivity depends on the bulk of the N-substituent present in UIs and on the substituents present in the ketene. Moore found that in reactions of CCK 17 with UIs, the use of a bulky N-t-Bu group induces a complete endo selectivity, while the use of a less demanding N-p-methoxyphenyl group induces an exo selectivity.⁸ An stereochemical analysis of lactams δ-20 and β-21 indicates that both reactions experimentally take place along the endo stereoisomeric channels (see Scheme 4).^8,9 Consequently, only the endo channels associated with the formation of δ-lactams and β-lactams were analysed. In addition, two conformations for UIs 18 and 19, the s-trans and the s-cis ones, are feasible. The s-trans conformations are 1.8 (s-trans 18) and 5.4 (s-trans 19) kcal mol⁻¹ more stable than the s-cis ones. Consequently, the endo/s-trans channels were selected for the initial nucleophilic attack.

The first step of these polar reactions is the nucleophilic attack of the N1 nitrogen of UIs 18 and 19 on the C6 carbon of CCK 17 to yield ZW intermediates ZW-st-18 and ZW-st-19. As the two reagents approach each other, the formation of the C–N single bond takes place without any appreciable barrier; formation of ZW-st-18 and ZW-sc-19 being strongly exothermic, −25.6 and −28.6 kcal mol⁻¹. These energy results agree with the high electrophilic character of CCK 17, ω = 2.20 eV,³⁸ and the high nucleophilic character of these UIs, N = 3.61 eV (18) and 3.74 eV (19),³⁹ which favour polar reactions.²⁴

These ZW intermediates can be converted into β-lactams β-24 and β-21, the products of the Staudinger reaction, through the subsequent C2–C5 single bond formation. From these ZW intermediates, the activation enthalpies associated with the cyclisation processes are 21.2 (TS-2-18) and 19.0 (TS-2-19) kcal mol⁻¹; formation of the corresponding β-lactams being strongly exothermic, −40.6 (β-24) and −42.4 (β-21) kcal mol⁻¹.

Due to the C2–C3 free bond rotation in the s-trans ZW-st-18 and ZW-st-19, they can equilibrate with the s-cis ZW-sc-18 and ZW-sc-19. The activation enthalpies associated with the C2–C5 single bond rotation are 10.6 (TS-rot-18) and 11.3 (TS-rot-19) kcal mol⁻¹. As expected, the s-cis conformations are 5.0 (ZW-sc-18) and 7.9 (ZW-sc-19) kcal mol⁻¹ more energetic than the s-trans ones.

From the s-cis intermediates ZW-sc-18 and ZW-sc-19, the subsequent ring closure via the C4–C6 single bond formation yields the δ-lactams δ-20 and δ-25, the products of the ADA reaction. The activation enthalpies associated with the formation of the C4–C6 single bond are 9.2 (TS-4-18) and 12.0 (TS-4-19) kcal mol⁻¹; formation of the δ-lactams being strongly exothermic, −50.0 (δ-20) and −45.3 (δ-25) kcal mol⁻¹. Formation of δ-lactams from ZW-sc-18 and ZW-sc-19 is kinetically more favourable than formation of β-lactams from the s-trans ones. Interestingly, the activation enthalpies associated with the formation of β-lactams are ca. 10 kcal mol⁻¹ higher than those associated with the formation of δ-lactam. These results are probably a consequence of the strain associated with the formation of the four-membered TS-2-R.

Inclusion of entropies to enthalpies increases the free energies between 12–18 kcal mol⁻¹ as a consequence of unfavourable entropies associated with these bimolecular processes. A schematic representation of the free energy profiles of the two competitive channels for the reactions of CCK 17 with UIs 18 and 19 is given in Fig. 1.

Fig. 1 MPWB1K/6-311G(d,p) free energy profiles (in kcal mol⁻¹) in DEE of the reactions of CCK 17 with UIs 18, up, and 19, down. The most favourable reactive channels associated with the formation of lactams δ-20 and β-21 are given in blue.

As the rotational TSs are below the TSs associated with cyclisations, in the free energy scale, the s-trans and s-cis ZW intermediates are in equilibrium. Consequently, the Curtin–Hammett principle⁴⁰ can be applied in these competitive channels. Thus, for the reaction of CCK 17 with UI 18, the most favourable channel for the cyclisation corresponds to the formation of δ-lactam δ-20 via TS-4-18, while for the reaction with UI 19, the most favourable channel corresponds to the formation of β-lactam β-21 via TS-2-19 in complete agreement with the experimental results.

What is the origin of the selectivity experimentally observed in the formation of β- or δ-lactams in the reactions of CCK 17 with UIs 18 and 19? A comparison of the activation free energies associated with the ring closure processes along the two competitive channels indicates that the formation of δ-lactams, the products of the ADA reaction, is energetically more favoured than the formation of the more strained β-lactams, the products of the Staudinger reaction (see Table 1 and Fig. 1). However, if the s-trans/s-cis conformational equilibrium in the ZW intermediates is considered, the relative free energies of the TSs associated with the ring-closure processes, TS-2-R and TS-4-R, must be considered.⁴⁰

For the reaction with the phenyl-substituted UI 18, TS-4-18 is located 5.5 kcal mol⁻¹ below TS-2-18. This high free energy difference accounts for the complete formation of lactam δ-20, in clear agreement with the experimental results. However, when the diphenyl-substituted UI 19 is considered, TS-2-19 is located 2.2 kcal mol⁻¹ below TS-4-19. This energy result accounts for the selectivity found experimentally in the formation for lactam β-21, being in complete agreement with the change in selectivity respect to the reaction with phenyl-substituted UI 18.

An analysis of the geometries of the TSs associated with the formation of δ-lactams shows that while at TS-4-18 the phenyl substituent is far from the ketene residue, at TS-4-19 the second phenyl substituent is close to it. A steric hindrance present at TS-4-19, which increases the relative free energy of TS-4-19 by 4.1 kcal mol⁻¹ with respect to that of TS-4-18, could be responsible for the change of selectivity. Consequently, in absence of a steric hindrance, formation of δ-lactams appears to be favoured over the formation of β-lactams.

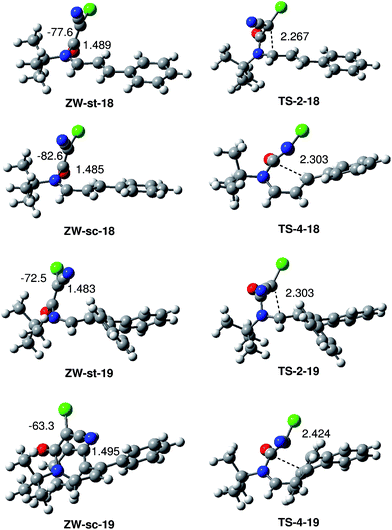
The structure of the ZW intermediates and TSs associated with the formation of the β-lactams and δ-lactams in the reactions of CCK 17 with UIs 18 and 19 are shown in Fig. 2. At the four ZW intermediates, the length of the C6–N1 single bond is ca. 1.49 Å. At these intermediates, both the ketene and the UI frameworks are not completely perpendicular since the C2–N1–C6–C5 dihedral angles at these ZW intermediates are: −77.6 (ZW-st-18), −82.6 (ZW-sc-18), −72.5 (ZW-st-19) and −63.3 (ZW-sc-19) degrees. Interestingly, this slight twist approaches the C6 carbon of the ketene framework towards the C2 and C4 carbon of the UI frameworks, thus favouring the subsequent cyclisation process.

Fig. 2 Structures of the ZW intermediates and TSs associated with the formation of β-lactams and δ-lactams in the reactions of CCK 17 with UIs 18 and 19. The distances are given in Angstroms, while the dihedral angles are given in degrees.

At the TSs associated with the formation of the β-lactams, the distance between the C2 and C5 carbons is 2.267 Å (TS-2-18) and 2.303 Å (TS-2-19) Å, while at the TSs associated with the formation of the δ-lactams, the distance between the C4 and C5 carbons is 2.303 Å (TS-4-18) and 2.424 (TS-4-19) Å. These TSs are slightly more delayed than those associated with the formation of β-lactams.

The polar nature of these reactions was analysed by computing the global electron density transfer (GEDT) at the ZW intermediates ZW-st-18 and ZW-st-19. The natural atomic charges at these species, obtained through a natural population analysis (NPA), were shared between the ketene and the UI frameworks. The values of the GEDT that fluxes from the UI framework to the ketene are 0.63e (ZW-st-18) and 0.62e (ZW-st-19). The very high GEDT found at these intermediates points to their high zwitterionic character and their large stability, in clear agreement with the high electrophilic character of CCK 17 and the high nucleophilic character of UIs 18 and 19.

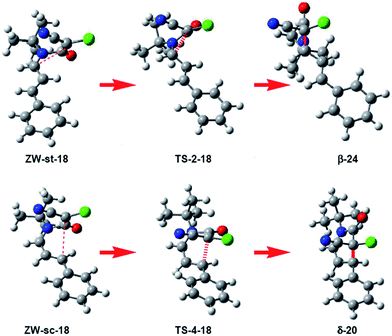
What is the origin of the cis/trans selectivity in the formation of lactam δ-20 and β-21? Both reactions are experimentally completely cis/trans selective, i.e. while the cyano and phenyl substituent in δ-lactam δ-20 presented a cis relation, the cyano and vinyl substituent in β-lactam β-21 presented a trans relation (see Scheme 4).^8,9 The geometries of the species involved in the formation of lactams β-24 and δ-20 are given in Fig. 3. These lactams come from the ring closure at ZW intermediates ZW-st-18 and ZW-sc-18, respectively. In these ZW intermediates, the ketene and imine frameworks are in an almost perpendicular rearrangement in which the sp² hybridisated C5 carbon is located above the sp² hybridisated C2 and C4 carbons (see Fig. 3). Consequently, along the cyclisation processes, formation of the new C–C single bonds does not require any specific rotation as has been poposed.⁵ Along the endo approach mode of UI 18 to CCK 17, the trans N1–C2 configuration present in ZW-st-18 remains at TS-2-18; consequently, the cyano group and the chain present at C2 remain with a trans relationship along the formation of β-lactam β-24. However, along the formation of δ-lactam δ-20, the C2–C3 bond rotation demanded in ZW-st-18 to reach TS-4-18 changes the relative position of the phenyl group present in C4, and now, along the formation of δ-lactam δ-20, the cyano and phenyl substituents present a cis relation, in clear agreement with the experimental outcomes.

Fig. 3 Geometrical changes along the formation of β-lactam β-24 and δ-lactam δ-20. While β-24 presents a trans diastereoisomeric relation of the CN group relative to the chain, δ-20 presents a cis disposition of the CN group relative to the phenyl substituent.

Finally, the ZW intermediates involved in Staudinger reactions are represented by a Lewis structure in which the C5–C6 bond is drawn by C–C single bond (see structure 9 in Scheme 2). However, a NBO analysis in the ZW intermediates ZW-st-18 and ZW-sc-18 provides a C5–C6 Wiberg bond index of 1.35 (see Scheme 7). This value, together with the high activation energy associated with TS-rot2-18 involved in the endo/exo equilibration in the s-trans zwitterionic intermediate ZW-st-18 via a C5–C6 bond rotation, 36.0 kcal mol⁻¹, rule out the endo/exo stereoisomeric conversion in the ZW intermediates ZW-st-18 and ZW-sc-18.

(ii) ELF topological analysis of the two competitive channels associated with the stepwise reaction between CCK 17 and UI 18 yielding lactams δ-20 and β-24

Recent theoretical works have emphasised that the ELF topological analysis along a reaction path is a valuable tool to understand the bonding changes along the reaction path, and thus to characterise the molecular mechanism.^11,12 A great deal of work characterising the mechanisms of significant organic reactions involving the formation of new C–C single bonds have shown that it begins in the short C–C distance range of 1.9–2.0 Å by merging two monosynaptic basins, V(Cx) and V(Cy), into a new disynaptic basin V(Cx,Cy) associated with the formation of the new Cx–Cy single bond.⁴¹ The Cx and Cy carbons characterised by the presence of the monosynaptic basins, V(Cx) and V(Cy), have been called pseudoradical centres.⁴²

In the present section, an ELF topological analysis of the MPWB1K/6-311G(d,p) wavefunctions of the most relevant points associated with the formation of β-lactam β-24, the product of a Staudinger reaction, and δ-lactam δ-20, the product of an ADA reaction, has been performed in order to characterise the molecular mechanism of these competitive reactions. The corresponding ELF topological analysis is given in the ESI.†

From the ELF topological analysis of bonding changes along the two competitive channels associated with the stepwise reaction between CCK 17 and UI 18 yielding lactams δ-20 and β-24 some interesting conclusions can be drawn: (i) along the nucleophilic attack of UI 18 on CCK 17, the formation of the new N1–C6 single bond begins at a N1–C6 distance of 1.92 Å, by merging the electron density of two V(N1) and V(C6) monosynaptic basins located at the N1 and the C6 atoms. The electron density of the new N1–C6 single bond comes mainly from the N1 lone pair present at UI 18; (ii) at this N1–C6 distance, the electronic structure of the C–C double bonds of UI 18 remains unchanged. Consequently, the conjugated system of UI 18 does not participate on the formation of the N1–C6 single bond; (iii) the two competitive cyclisation processes are topologically very similar. Formation of the C2–C5 or C4–C5 single bonds take place at a C–C distance of 2.009 and 1.941 Å, respectively, by merging the electron density of the corresponding two pseudoradical centers,⁴¹ with an initial population of 1.38 and 1.45e; (iv) the population of the V(N1,C6) disynaptic basin at TS-4-18 and TS-2-18, 2.09 and 1.90e, respectively, which is associated with the N1–C6 single bond created in the first step of the reaction, makes it possible to rule out the proposed electrocyclic mechanism along these ring closure processes.^5,10d

Note that at the TS associated with the electrocyclic aperture of cyclobutene 22, the population of the V(C1,C2) disynaptic basin is 3.17e as a consequence of the conjugation along the C4–C1–C2–C3 framework (see Scheme 6).¹³

Conclusions

The molecular mechanism of the reactions of the electrophilic CCK 17 with the nucleophilic UIs 18 and 19, yielding β-lactams, i.e. Staudinger reaction, products or δ-lactams, i.e. ADA reaction products, has been investigated using DFT methods at the MPWB1K/6-311G(d,p) computational level in DEE. These reactions present stepwise mechanisms. The reactions are initialised by the nucleophilic attack of the nitrogen lone pair of the s-trans UIs on the carbonyl carbon atom of the ketene, with formation of very stable ZW intermediates. The subsequent C–C single bond formation at the imine carbon of the s-trans ZW intermediates allows the formation of β-lactams. However, the facile C–C bond rotation at these ZW intermediates allows s-trans conformations to be in equilibrium with the more energetic s-cis ones. The subsequent C–C single bond formation at the β-conjugated position of the UIs allows the formation of δ-lactams.

Analysis of the relative free energies of the stationary points found along the endo competitive channels indicates that the C–C single bond formation yielding δ-lactams, the product of the ADA reaction, is energetically more favourable than that resulting in β-lactams, the product of the Staudinger reaction, due to the strain associated with the formation of the corresponding four-membered TS. However, if the s-trans/s-cis conformational equilibrium at the corresponding zwitterionic intermediates is considered, an appealing conclusion is obtained: while in the reaction involving phenyl substituted UI 18, the channel associated with formation of the δ-lactam via TS-4-18 is clearly favoured over that associated with formation of the β-lactam via TS-2-18, the presence of the second phenyl substituent in UI 19 increases the free energy of TS-4-19 associated with the formation of the δ-lactam, and decreases slightly the activation free of TS-2-19, thus favouring the formation of the β-lactam.

An ELF topological analysis along the reaction channels associated with the formation β- and δ-lactams provides relevant information about the C–N and C–C bond formation along the two competitive reactive channels. The ELF quantum topology analysis of the changes in electron density along the ring closure in ZW-st-18 makes it possible to reject both an electrocyclic mechanism based on the pericyclic reaction model for these ring closure processes, as well as the reactivity model based on the analysis of MOs to explain both cis/trans selectivity and the formation of δ- versus β-lactam. The amount of energy required for changes in electron density at the ground state of the reagents along an organic reaction, and not MO interactions as proposed by the FMO theory, are responsible for the feasibility of a reaction path.⁴¹

References

1. (a) R. Southgate and S. Elson, The Chemistry of Organic Natural Products, Springer-Verlag, Wien, 1985; (b) R. Southgate, C. Branch, S. Coulton and E. Hunt, Recent Progress in the Chemical Synthesis of Antibiotics and Related Microbial Products, Springer-Verlag, Berlin, 1993, p. 621; (c) R. Southgate, Contemp. Org. Synth., 1994, 1, 417.
2. (a) H. Staudinger, Justus Liebigs Ann. Chem., 1907, 356, 51; (b) T. T. Tidwell, Ketenes, John Wiley & Sons, New York, 1995.
3. The Organic Chemistry of beta-Lactams, ed. G. I. Georg, Verlag Chemie, New York, 1993.
4. (a) C. Palomo, J. M. Aizpurua, I. Ganboa and M. Oiarbide, Eur. J. Org. Chem., 1999, 3223; (b) G. S. Singh, Tetrahedron, 2003, 59, 7631; (c) C. Palomo, J. M. Aizpurua, I. Ganboa and M. Oiarbide, Curr. Med. Chem., 2004, 11, 1837; (d) B. Alcaide, P. Almendros and C. Aragoncillo, Chem. Rev., 2007, 107, 4437; (e) A. Brandi, S. Cicchi and F. M. Cordero, Chem. Rev., 2008, 108, 3988.
5. F. P. Cossío, A. Arrieta and M. A. Sierra, Acc. Chem. Res., 2008, 41, 925.
6. (a) Y. Liang, L. Jiao, S. W. Zhang and J. X. Xu, J. Org. Chem., 2005, 70, 334; (b) L. Jiao, Y. Liang and J. X. Xu, J. Am. Chem. Soc., 2006, 128, 6060; (c) Y. K. Wang, Y. Liang, L. Jiao, D.-M. Du and J. X. Xu, J. Org. Chem., 2006, 71, 6983; (d) B. N. Li, Y. K. Wang, D.-M. Du and J. X. Xu, J. Org. Chem., 2007, 72, 990; (e) L. B. Hu, Y. K. Wang, B. N. Li, D.-M. Du and J. X. Xu, Tetrahedron, 2007, 63, 9387.
7. I. Arrastia, A. Arrieta, J. M. Ugalde, F. P. Cossío and B. Lecea, Tetrahedron Lett., 1994, 42, 7825.
8. H. W. Moore and G. Hughes, Tetrahedron Lett., 1982, 23, 4003.
9. W. T. Brady and C. H. Shieh, J. Org. Chem., 1983, 48, 2499.
10. (a) J. A. Sordo, J. González and T. L. Sordo, J. Am. Chem. Soc., 1992, 114, 6249; (b) F. P. Cossío, J. M. Ugalde, X. López, B. Lecea and C. Palomo, J. Am. Chem. Soc., 1993, 115, 995; (c) F. P. Cossío, A. Arrieta, B. Lecea and J. M. Ugalde, J. Am. Chem. Soc., 1994, 116, 2085; (d) A. Arrieta, B. Lecea and F. P. Cossío, J. Org. Chem., 1998, 63, 5869; (e) A. Arrieta, F. P. Cossío, I. Fernández, M. Gómez-Gallego, B. Lecea, M. J. Mancheno and M. A. Sierra, J. Am. Chem. Soc., 2000, 122, 11509; (f) A. Venturini and J. González, J. Org. Chem., 2002, 67, 9089; (g) B. K. Banik, B. Lecea, A. Arrieta, A. de Cózar and F. P. Cossío, Angew. Chem., Int. Ed., 2007, 46, 3028; (h) I. Fernández, M. A. Sierra, M. J. Mancheno, M. Gómez-Gallego and F. P. Cossío, J. Am. Chem. Soc., 2008, 130, 13892.
11. C. W. Jefford, G. Bernardelli, Y. Wang, D. C. Spellmeyer, A. Buda and K. N. Houk, J. Am. Chem. Soc., 1992, 114, 1157.
12. (a) V. Polo, J. Andrés, S. Berski, L. R. Domingo and B. Silvi, J. Phys. Chem. A, 2008, 112, 7128; (b) J. Andrés, P. González-Navarrete and V. S. Safont, Int. J. Quantum Chem., 2014, 114, 1239.
13. J. Andrés, S. Berski, L. R. Domingo, V. Polo and B. Silvi, Curr. Org. Chem., 2011, 15, 3566.
14. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397.
15. (a) A. Savin, A. D. Becke, J. Flad, R. Nesper, H. Preuss and H. G. Vonschnering, Angew. Chem., Int. Ed., 1991, 30, 409; (b) B. Silvi and A. Savin, Nature, 1994, 371, 683; (c) A. Savin, B. Silvi and F. Colonna, Can. J. Chem., 1996, 74, 1088; (d) A. Savin, R. Nesper, S. Wengert and T. F. Fassler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808.
16. (a) S. Berski, J. Andrés, B. Silvi and L. R. Domingo, J. Phys. Chem. A, 2003, 107, 6014; (b) S. Berski, J. Andrés, B. Silvi and L. R. Domingo, J. Phys. Chem. A, 2006, 110, 13939.
17. K. Fukui, J. Phys. Chem., 1970, 74, 4161.
18. K. N. Houk, J. González and Y. Li, Acc. Chem. Res., 1995, 28, 81.
19. F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry. Part A: Structure and Mechanisms, Springer, New York, 2000.
20. R. B. Woodward and R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1969, 8, 781.
21. B. Lecea, I. Arrastia, A. Arrieta, G. Roa, X. López, M. I. Arriortua, J. M. Ugalde and F. P. Cossío, J. Org. Chem., 1996, 61, 3070.
22. K. N. Houk, J. Sims, C. R. Watts and L. J. Luskus, J. Am. Chem. Soc., 1973, 95, 7301.
23. International Union of Pure and Applied Chemistry, Compendium of Chemical Terminology, Gold Book, version 2.3.3, 2014.
24. L. R. Domingo and J. A. Sáez, Org. Biomol. Chem., 2009, 7, 3576.
25. Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 6908.
26. W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab initio Molecular Orbital Theory, Wiley, New York, 1986.
27. (a) H. B. Schlegel, J. Comput. Chem., 1982, 3, 214; (b) Modern Electronic Structure Theory, ed. H. B. Schlegel and D. R. Yarkony, World Scientific Publishing, Singapore, 1994.
28. (a) C. González and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523; (b) C. González and H. B. Schlegel, J. Chem. Phys., 1991, 95, 5853.
29. (a) J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027; (b) B. Y. Simkin and I. Sheikhet, Quantum Chemical and Statistical Theory of Solutions – Computational Approach, Ellis Horwood, London, 1995.
30. (a) E. Cances, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032; (b) M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327; (c) V. Barone, M. Cossi and J. Tomasi, J. Comput. Chem., 1998, 19, 404.
31. (a) A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735; (b) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.
32. S. Noury, X. Krokidis, F. Fuster and B. Silvi, Comput. Chem., 1999, 23, 597.
33. M. J. Frisch, et al., Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
34. R. G. Parr, L. v. Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922.
35. (a) R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512; (b) R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989.
36. (a) L. R. Domingo, E. Chamorro and P. Pérez, J. Org. Chem., 2008, 73, 4615; (b) L. R. Domingo and P. Pérez, Org. Biomol. Chem., 2011, 9, 7168.
37. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133.
38. L. R. Domingo, M. J. Aurell, P. Pérez and R. Contreras, Tetrahedron, 2002, 58, 4417.
39. P. Jaramillo, L. R. Domingo, E. Chamorro and P. Pérez, J. Mol. Struct.: THEOCHEM, 2008, 865, 68.
40. (a) D. Y. Curtin, Rec. Chem. Prog., 1954, 15, 111; (b) J. I. Seeman, Chem. Rev., 1983, 83, 83.
41. L. R. Domingo, RSC Adv., 2014, 4, 32415.
42. L. R. Domingo, E. Chamorro and P. Pérez, Lett. Org. Chem., 2010, 7, 432.

---

Footnote

† Electronic supplementary information (ESI) available: Complete ELF topological analysis of the two competitive channels associated with the stepwise reaction between CCK 17 and UI 18 yielding lactams β-24 and δ-20. MPWB1K/6-311G(d,p) electronic energies, enthalpies, entropies, free energies and cartesian coordinates of the stationary structures involved in the reactions of CCK 17 with UIs 18 and 19. MPWB1K/6-31G(d) electronic chemical potential μ, chemical hardness η, global electrophilicity ω, and global nucleophilicity N indices of ketene 17, and UIs 18 and 19. MPWB1K/6-311G(d,p) cartesian coordinates of the stationary structures involved in the reactions of CCK 17 with UIs 18 and 19. See DOI: 10.1039/c4ra10291f

---