CO₂ adducts of Lewis acid–base pairs (LBCO₂LA; LB = PMe₃, NHC and LA = AlH₃, AlCl₃, BH₃) − analogous to carboxylic acids and their derivatives

Abstract

The relationship between the structure and bonding of two different classes of molecules helps to understand and correlate their physiochemical activity. Here, we report the structure-bonding analogy between CO₂ adducts of a Lewis acid (LA)–Lewis base (LB) pairs, LBCO₂LA (LB = PMe₃ and NHC; LA = AlH₃, AlCl₃ and BH₃) and carboxylic acids and their derivatives, RCO₂R′ (R, R′ = alkyl, H) by quantum mechanical calculations. The direction of charge flow in LBCO₂LA is from LB to LA, whereas the reverse direction of charge flow (R′ to R) is observed for RCO₂R′ leading to a formally negatively charged CO₂ group (²A₁) in both systems. This negatively charged bent CO₂ group plays a deterministic role towards its bonding interaction with other fragments. The bonding analysis by the EDA-NOCV method indicates that both the LB and R groups form an electron sharing bond with the carbon atom of the bent CO₂ fragment, whereas both LA and R′ form a donor–acceptor interaction with the oxygen atom. Our analysis suggests that the CO₂ adducts of the Lewis acid (LA)–Lewis base (LB) pairs, LBCO₂LA, can be considered as inorganic analogues of carboxylic acids and their derivatives, RCO₂R′.

---

Introduction

The structure–activity relationship has a very prominent role in chemistry, which is based on the concept of understanding the physiochemical activity of a compound in relation to its molecular structure. The terms isoelectronic, isostructural, isolobal, isoreactive etc. are commonly used to correlate and draw a parallel between different types of molecules.¹ The similarities between benzene and borazine,² ethane and ammonia–borane adduct,² the diagonal relationship between the first row and the second row elements viz., boron and silicon,³ carbon and phosphorous⁴ are some of the classical examples. Here, we report the structure-bonding analogy between CO₂ adducts of Lewis acid (LA)–Lewis base (LB) pairs, LBCO₂LA, as well as carboxylic acids and their derivatives, RCO₂R′, (Scheme 1a).

Scheme 1 Schematic representation of the analogy between the experimentally reported (a) carboxylic acids, its derivatives and CO₂ adducts of LA–LB pairs, (b) carboxylate anions and LB coordinated CO₂ and (c) protonated carboxylic acids, bis-LA coordinated carboxylate anion and adduct of CO₂ with two LAs and one LB. The ‘≡’ sign indicates structural equivalence.

It has been reported that the sterically demanding frustrated LA–LB adducts show high reactivity towards a variety of small molecules such as inert CO₂ at ambient conditions.⁵ Recently, CO₂ activation by less sterically demanding LA–LB pairs (Me₂PCH₂AlMe₂)₂ and (Ph₂PCH₂AlMe₂)₂ by Fontaine and co-workers are also reported.⁶ These adducts show bent geometry for CO₂ as that of the carboxylic acid derivatives RCO₂R′ (Scheme 1a). In addition to the apparent structural similarities, reports of several adducts in the literature (Scheme 1b and c) indicate that LBCO₂LA and RCO₂R′ might possess similarity in the reactivity as well.⁷

Note that, the CO₂ adduct of N-heterocyclic carbene, which can be considered as analogous to carboxylate anion (Scheme 1b)^7a have been synthesized. In addition, CO₂ adduct of two LAs and one LB, [R₃PCO₂(AlX ₃)₂]^5b,c,h as well as the mixed adduct of the carboxylate anion with two LAs, RCO₂[B(C₆F₅)₃]₂⁻,^7b,c which are analogous to the protonated carboxylic acid (Scheme 1c) have also been reported. These examples show possible corroboration for the structure-bonding analogy between carboxylic acid and CO₂ adduct of LA–LB pairs. However, the usual bonding description between the R, R′ group and CO₂ in RCO₂R′ is considered to be a covalent electron sharing. On the other hand, the LB and LA are commonly known to form donor–acceptor bonds and thus the CO₂ adduct of the LA–LB pairs could also be considered as space separated donor–acceptor complex.⁸ Therefore, the following logical questions arise. Whether the bonding interaction of CO₂ with the rest of the fragments in these two structurally similar classes of compounds is also similar? Could the CO₂ adduct of LA–LB pairs be considered as a space separated donor–acceptor complex?

In order to explore the nature of bonding of CO₂ fragment with LA and LB in LBCO₂LA, we have carried out the quantum mechanical calculations at the BP86/TZ2P level of theory^9,10 on the CO₂ adduct of LA–LB pairs (LBCO₂LA) (1–6, Fig. 1), where LB (LB = PMe₃ and NHC) is coordinated to the C-atom and LA (LA = AlH₃, AlCl₃ and BH₃) is coordinated to one of the O-atom of bent CO₂. The bonding pattern of CO₂ with LA and LB in LBCO₂LA have been compared with the corresponding bonding pattern in carboxylic acids and derivatives, RCO₂R′, where R and R′ = H and CH₃ (7–9, Fig. 1). We have analysed the bonding situation in these two apparently different classes of molecules in detail by the EDA method,¹¹ which has been successfully employed by Frenking and co-workers to understand the best bonding description.¹²

Fig. 1 Optimized geometries (BP86/TZ2P) and important geometrical parameters of Me₃PCO₂AlH₃ (1), Me₃PCO₂AlCl₃ (2), Me₃PCO₂BH₃ (3), NHCCO₂AlH₃ (4), NHCCO₂AlCl₃ (5), NHCCO₂BH₃ (6), HCO₂H (7), CH₃CO₂H (8) and CH₃CO₂CH₃ (9). Distances are given in Å and angles are given in deg. Point group symmetry are given in parenthesis.

Results and discussion

The equilibrium geometries of Me₃PCO₂AlH₃ (1), Me₃PCO₂AlCl₃ (2), Me₃PCO₂BH₃ (3), NHCCO₂AlH₃ (4), NHCCO₂AlCl₃ (5), NHCCO₂BH₃ (6), HCO₂H (7), CH₃CO₂H (8) and CH₃CO₂CH₃ (9) at the BP86/TZ2P level of theory are shown in Fig. 1.^9,10

The geometrical parameters of 1–9 are reasonably close to the available experimentally reported values, which supports the adequacy of the level of theory used (Table S4†).^5c,g,h,i The coordinated C–O bonds are slightly longer, whereas the uncoordinated C–O bonds are slightly shorter in RCO₂R′ (7–9) as compared to LBCO₂LA (1–6). Note that, the CO₂ group in LBCO₂LA is significantly bent similar to that in RCO₂R′. The bending angle in 1–6 is in the range of 128.7–134.2°, which is slightly larger than those in RCO₂R′, 7–9 (122.4–125.4°). Since the CO₂ fragment is significantly bent in both the LBCO₂LA adducts and RCO₂R′, the bonding in these molecules can be best analysed by the interaction of the bent CO₂ fragment with LB and LA in 1–6 as well as with R and R′ in 7–9.¹³ A correlation diagram connecting the important molecular orbitals (MO) of linear and bent geometries of singlet CO₂ reveals the nature of the frontier orbitals, which can interact with LB and R as well as with LA and R′ (Fig. 2). The linear CO₂ possesses a pair of mutually perpendicular degenerate non-bonding HOMO (−10.71 eV) having coefficient on the terminal O-atoms. It also has degenerate antibonding π* LUMO+1 (0.85 eV) with major coefficient on the central carbon atom.¹⁴ Each of the two mutually perpendicular set of π-MOs of bent CO₂ can be considered as similar to the 3c–4e π-MOs in the allylic anion.

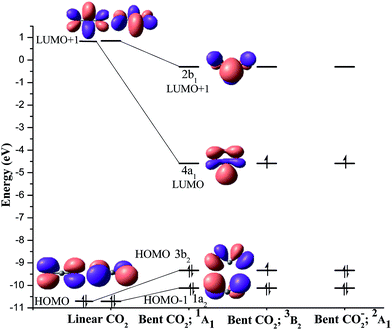Fig. 2 Correlation diagram connecting the frontier molecular orbitals of linear CO₂ and singlet bent CO₂ (¹A₁) at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory.¹³ The nature of the molecular orbitals of the triplet bent CO₂ (³B₂) and doublet bent CO₂⁻ (²A₁) are also shown.

The HOMO of linear CO₂ is destabilized in bent CO₂ (3b₂ and 1a₂) due to the increased antibonding interaction between the p-orbitals on the O-atoms. This implies enhancement in the nucleophilic character of the terminal O-atoms. On the other hand, one of the degenerate π*-MOs in linear CO₂ is highly stabilized (4a₁, −4.59 eV) in the bent CO₂ as compared to the other (2b₁, −0.30 eV; Fig. 2). This stabilization is attributed to the enhanced bonding interaction in the in-plane MO (4a₁, LUMO). Hence, the electrophilic character on the central carbon atom also enhances in bent CO₂ as compared to linear CO₂. Note that, the extent of stabilization of LUMO+1 is much higher than the destabilization of HOMO, which indicates significant enhancement of the electrophilic character in bent CO₂ as compared to the nucleophilic character. The increased philicity of bent CO₂ in (PPh₃)₂CCO₂ has also been reported by Frenking and co-workers.¹⁵ Hence any factor, which causes the bending of CO₂, increases the reactivity and would therefore favour the functionalization.

Apparently, the bonding description of the LBCO₂LA adducts (1–6) can be assumed as the donation of the lone pair from LB to the electrophilic carbon atom of the bent CO₂ (4a₁, LUMO, Fig. 2) as well as the donation of the lone pair from oxygen atom of bent CO₂ (3b₂, HOMO, Fig. 2) to the empty orbital of LA. On the other hand, the bent CO₂ group in RCO₂R′ can be assumed in the singly excited state (³B₂, Fig. 2) that can form electron sharing bonds with R and R′.¹⁶ In order to verify the best bonding description for the interaction of the bent CO₂ with the rest of the fragments in 1–9, we have carried out detailed bonding analysis by NBO¹⁷ and EDA-NOCV methods.^11,18

NBO group charge analysis in 1–6 (Table 1) shows high positive charge on LB and the negative charge is distributed over CO₂ and LA, where CO₂ carries higher negative charge (−0.44 to −0.72e) than LA (−0.14 to −0.33e). On the other hand, the R′ group in 7–9 (0.31 to 0.49e) carries higher positive charge than the R group (−0.01 to 0.11e). Hence, the net charge flow in 7–9 is from the R′ to R via CO₂ group, where CO₂ group acquires a negative charge (−0.30 to −0.60e). The direction of charge flow in LBCO₂LA is from LB to LA, whereas the reverse direction of charge flow (R′ to R) is observed for RCO₂R′ suggesting a formally negatively charged CO₂ fragment (²A₁, 1a₂²3b₂²4a₁¹) in these molecules. This is consistent with the MO analysis that the bent CO₂ has higher electrophilicity than nucleophilicity.¹⁵

Table 1 Group charges in PMe₃CO₂AlH₃ (1), PMe₃CO₂AlCl₃ (2), PMe₃CO₂BH₃ (3), NHCCO₂AlH₃ (4), NHCCO₂AlCl₃ (5), NHCCO₂BH₃ (6), HCO₂H (7), CH₃CO₂H (8) and CH₃CO₂CH₃ (9) as obtained from the natural bond orbital analysis at the M06/def2-TZVPP//BP86/TZ2P level of theory

1		2		3		4		5		6		7		8		9
PMe3	0.85	PMe3	0.88	PMe3	0.79	NHC	0.76	NHC	0.72	NHC	0.75	H	0.11	CH3	−0.01	CH3	−0.01
CO2	−0.71	CO2	−0.72	CO2	−0.46	CO2	−0.61	CO2	−0.63	CO2	−0.44	CO2	−0.60	CO2	−0.48	CO2	−0.30
AlH3	−0.14	AlCl3	−0.16	BH3	−0.33	AlH3	−0.15	AlCl3	−0.09	BH3	−0.31	H	0.49	H	0.49	CH3	0.31

---

If LBCO₂LA (1–6) is a space separated donor–acceptor complex,⁸ the bonding interaction of CO₂ with LB and LA fragments could be considered as donor–acceptor type viz., LB → C_CO2LA and _LBCO2O → LA. On the other hand, if the CO₂ fragment in 7–9 is assumed to form electron sharing bonds with R and R′, the bonding interaction would then be an electron sharing type viz., R–C_CO2R′ and _RCO2O–R′.¹⁹ Here, we have explored the possibility of both electron sharing as well as donor–acceptor type bonding of CO₂ group with other fragments in 1–9 (Scheme 2). The appropriate formal charges are assigned to the corresponding fragments to maintain the correct electronic configuration. The bond formed between the LB and C-atom of CO₂LA can be of two types. The first possibility is the donor–acceptor interaction from the lone pair of LB to the empty orbital of the CO₂LA fragment (similar to the LUMO, 4a₁ of bent CO₂, Fig. 2), which is represented as LB → C_CO2LA in Scheme 2a and c.

Scheme 2 Schematic representation of the different types of bonding interactions of the CO₂ fragment in LBCO₂LA (1–6) and in RCO₂R′ (7–9).²⁰

The second possibility is the electron sharing ylidic-type interaction, which is represented as LB⁺–C_CO2LA⁻ in Scheme 2b and d. The electronic state of the fragments involved in these schemes are formed by transfer of one electron from the lone pair of LB to the empty orbital of CO₂LA (similar to the electronic state ²A₁ of bent CO₂⁻, Fig. 2), which results the formally positively charged LB⁺ and the negatively charged CO₂LA⁻ fragments.¹⁶ In either way, once LB is bonded to the in-plane LUMO of bent CO₂ (4a₁), the in-plane π-MOs can reorganize as in-plane lone pair orbital on each O-atom. The O-atom can donate the lone pair to the empty orbital on LA, which is represented in Scheme 2a and b. There may be another possibility that one electron from the lone pair on the O-atom (similar to 3b₂, Fig. 2) can be transferred to the vacant orbital on LA, which results LA⁻ and LBCO₂⁺ fragments having unpaired electrons. The interaction of LBCO₂⁺ and LA⁻ fragments results an ylidic type electron sharing _LBCO2O⁺–LA⁻ bond as shown in Scheme 2c and d. Similarly, two types of bonding interactions for the formation of bond between R and CO₂R′ as well as RCO₂ and R′ in 7–9 were also explored (Scheme 2e–h, Table S6†). The pertinent results of the EDA-NOCV analysis for the above mentioned bonding interactions (Scheme 2) are discussed next.

The complete EDA-NOCV results of 1, 4 and 9 are given in Table 2 and the EDA-NOCV results of the remaining molecules are similar and given in the ESI (Tables S1 and S2†). The electron sharing interactions for the ylidic type _PMe3P⁺–C_CO2AlH3⁻ (ΔE_orb = −153.5 kcal mol⁻¹) in 1 and _NHCC⁺–C_CO2AlH3⁻ (ΔE_orb = −219.0 kcal mol⁻¹) bonds in 4 (Scheme 2b and d) as well as electron sharing _CH3C–C_CO2CH3 bond (ΔE_orb = −210.8 kcal mol⁻¹) in 9 (Scheme 2f and h) has lower negative ΔE_orb values as compared to the corresponding donor–acceptor interactions. The ΔE_orb is the stabilization energy obtained by the overlap of the orbitals of the interacting fragments. The closer the electronic states of the interacting fragments to that in the molecule, the lesser will be the stabilization energy ΔE_orb. Hence, the interacting fragments, which lead to the lowest ΔE_orb can be considered as the best bonding fragments in terms of their electronic state.¹²

Table 2 The EDA-NOCV data for the interaction of the CO₂ fragment with the remaining fragments in PMe₃CO₂AlH₃ (1), NHCCO₂AlH₃ (4) and CH₃CO₂CH₃ (9) at the BP86/TZ2P level of theory using ADF 2013.01 package. Energies are in kcal mol⁻¹

Bond	1				4				9
	P → C	P^+–C^−	O → Al	O^+–Al^−	C → C	C^+–C^−	O → Al	O^+–Al^−	C^− → C^+	C–C	O^− → C^+	O–C
a Values in parenthesis give the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb.b Values in parenthesis give the percentage contribution to the orbital interaction ΔEorb.c ΔErest = ΔEorb − (ΔEσ + ΔEπ).
ΔEint	−66.4	−162.7	−39.8	−218.7	−85.8	−196.1	−36.4	−233.9	−332.3	−105.7	−280.6	−99.2
ΔEPauli	243.4	197.3	69.3	209.6	397.1	267.4	56.4	181.3	404.9	265.6	189.8	359.4
ΔEelstat^a	−136.8 (44.2%)	−206.6 (57.4%)	−65.8 (60.4%)	−199.3 (46.5%)	−222.5 (46.1%)	−244.5 (52.8%)	−57.9 (62.5%)	−179.0 (43.1%)	−380.5 (51.6%)	−160.5 (43.2%)	−248.9 (52.9%)	−159.8 (34.8%)
ΔEorb^a	−173.1 (55.8%)	−153.5 (42.6%)	−43.2 (39.6%)	−228.9 (53.5%)	−260.4 (53.9%)	−219.0 (47.2%)	−34.8 (37.5%)	−236.2 (56.9%)	−356.7 (48.4%)	−210.8 (56.7%)	−221.4 (47.1%)	−298.9 (65.2%)
ΔEσ^b	−144.6 (83.5%)	−123.9 (71.6%)	−22.7 (52.5%)	−211.5 (92.4%)	−213.4 (82.0%)	−182.3 (83.2%)	−21.2 (60.9%)	−225.9 (95.6%)	−314.0 (88.0%)	−184.8 (87.7%)	−174.8 (79.0%)	−279.9 (93.6%)
ΔEπ^b	−6.0 (3.5%)	−6.5 (3.8%)	−5.7 (13.9%)	−3.4 (1.5%)	−16.4 (6.3%)	−12.2 (5.6%)	−4.4 (12.6%)	−3.7 (1.6%)	−16.8 (4.7%)	−9.9 (4.7%)	−18.0 (8.1%)	−7.7 (2.6%)
ΔErest^b^,^c	−22.5 (13.0%)	−42.7 (24.7%)	14.8 (34.3%)	−14.0 (6.1%)	−30.6 (11.8%)	35.5 (16.2%)	9.2 (26.4%)	−6.6 (2.8%)	−25.9 (7.3%)	16.1 (7.6%)	−28.6 (12.9%)	−11.3 (3.8%)
ΔEprep	51.8	148.0	22.5	201.4	50.4	160.7	7.5	205.0	239.5	13.9	199.4	18.1
ΔE(−De)	−14.7	−14.7	−17.3	−17.3	−35.4	−35.4	−28.9	−28.9	−92.8	−92.8	−81.1	−81.1
ΔEorb/ΔEelstat	1.27	0.74	0.65	1.15	1.17	0.90	0.60	1.32	0.94	1.31	0.89	1.87

---

Hence, the bonding interaction of LB with CO₂LA can be best represented as 1,2-dipolar electron sharing interaction, in which LB carries a formal positive charge and the C-atom carries a formal negative charge (Scheme 2b and d). This bonding representation is consistent with the high value for the preparation energy of the fragments (Table 2 and S1†) and the positive NBO charge (Table 1) for the LB fragments. The ΔE_orb values also suggest that the classical electron sharing interaction between R and CO₂R′ is indeed the best bonding representation (Scheme 2f and h). The comparable ΔE_orb for the _NHCC–C_CO2AlH3 bond in 4 and _CH3C–C_CO2CH3 bond in 9 indicates that NHC can be considered as an appropriate substitution for the alkyl group for its coordination with CO₂ molecule. This is supported by the experimental report of NHCCO₂ (Scheme 1b), which is structurally equivalent to the carboxylate anion.^7a The preference for the electron sharing interaction of LB and R group with CO₂LA and CO₂R′ is duly reflected in the percentage of electrostatic contribution (ΔE_elstat). Note that, the LB–C_CO2LA bonds in 1–6 has higher percentage of electrostatic contribution (51.2–57.8%) as compared to covalent contribution, whereas the reverse trend (ΔE_elstat = 31.4–43.2%) is observed for the R–C_CO2R′ bonds in the carboxylic acids and its derivatives, 7–9. The ratio ΔE_orb/ΔE_elstat (Table S1†) for compounds 1–6 is less than one (varies from 0.73 to 0.95) and that for compounds 7–9 is higher than one (varies from 1.31 to 2.19). The ratio ΔE_orb/ΔE_elstat have been used earlier by Frenking and co-workers for describing the dative bond in Fischer carbenes and covalent bond in Schrock carbenes.^12a,b Although LB⁺–C_CO2LA⁻ and R–C_CO2R′ bonds are best represented by electron sharing interactions, the nature of the bonds in 1–6 varied significantly in terms of ΔE_orb/ΔE_elstat as compared to that in 7–9.

The α-NOCV pair of orbitals (Ψ₋₁/Ψ₁), deformation density plot (Δρ₁) and the corresponding energy (ΔE_σ) towards the dipolar electron sharing bond in 1 (ΔE_σ = −123.9 kcal mol⁻¹) and 4 (ΔE_σ = −182.3 kcal mol⁻¹) are shown in Fig. 3a and c. It clearly indicates the depletion of the electron density from LB⁺ and C-atom in CO₂LA⁻ as well as accumulation of electron density at the centre of the LB⁺−C_CO2LA⁻ bond. Similar plot of the deformation density in 9 (ΔE_σ = −184.8 kcal mol⁻¹) is obtained for the _CH3C–C_CO2CH3 bond as well (Fig. 3e). This is a typical deformation density plot for the electron sharing σ-bonds.¹⁸ The contribution from the π-type interaction is very negligible (Table 2, Fig. S1 and S2†). The ΔE_π comes from the hyperconjugative donation of the electrons from the perpendicular π-MO of the CO₂LA⁻/CO₂R′ fragment to the P–C_Me σ*-MO of PMe₃ in 1 (ΔE_π = −6.5 kcal mol⁻¹) and C–H σ*-MO in 9 (ΔE_π = −9.9 kcal mol⁻¹). However, the stronger π-acceptor NHC⁺ (vacant p-orbital) contributes to the higher ΔE_π (−12.2 kcal mol⁻¹) in 4. It is noteworthy that, the interaction energy between the LB⁺ and CO₂LA⁻ is significantly higher in 1 and 4 than that in carboxylic acid derivatives, 9. However, the calculated bond dissociation energies (D_e) are significantly low in 1 and 4 as compared to 9. The low value of D_e in 1 and 4 is attributed to the higher preparation energy required for promoting the fragments in their respective electronic excited states.

Fig. 3 The α-NOCV pair of orbitals (Ψ₋₁/Ψ₁) with their eigen values in parenthesis, the deformation density plots (Δρ₁) and the corresponding orbital stabilization energies ΔE_σ (kcal mol⁻¹) for the (a) _Me3PP⁺–C⁻_CO2AlH3 bond and (b) _Me3PCO2O → Al_AlH3 bond in 1, (c) _NHCC⁺–C⁻_CO2AlH3 bond and (d) _NHCCO2O → Al_AlH3 bond in 4, (e) _CH3C–C_CO2CH3 bond and (f) _CH3CO2O⁻ → C⁺_CH3 bond in 9 at the BP86/TZ2P level of theory. The direction of the charge flow is from red → blue. Isosurface value for NOCV pair of orbitals is 0.04 and that for the deformation density is 0.003.

The ΔE_orb for the donor–acceptor interaction _LBCO2O → LA in 1 (ΔE_orb = −43.2 kcal mol⁻¹), 4 (ΔE_orb = −34.8 kcal mol⁻¹) and _RCO2O⁻ → R′⁺ in 9 (ΔE_orb = −221.4 kcal mol⁻¹) have lower negative values as compared to the corresponding electron sharing interactions (Table 2). Hence, the bonding interaction between O-atom in LBCO₂ and LA can be considered as regular donor–acceptor interaction (Scheme 2a and b) and the bond formation between _RCO2O and R′ in RCO₂R′ can be best represented as 1,2-diploar donor–acceptor type interaction (Scheme 2e and f).²¹ Note that, according to the best bonding description of the carboxylic acids 7 and 8, the H-atom possesses a formal positive charge, which is consistent with the fact that the hydrogen atom of carboxylic acid is acidic. The EDA-NOCV data (Table 2 and S2†) suggest that the percentage of electrostatic contribution towards the donor–acceptor interaction for the _RCO2O⁻ → R′⁺ bonds in 7–9 is slightly higher than that for the _LBCO2O → B_BH3 bonds but lower than that for _LBCO2O → Al_AlH3/AlCl3 bonds in 1–6. The ΔE_orb/ΔE_elstat ratio (Table S2†) is in the range of 0.60 to 0.81 for _LBCO2O → Al_AlH3/AlCl3 bonds, 0.89 to 0.97 for _RCO2O⁻ → R′⁺ bonds and 1.09 and 1.11 for _LBCO2O → B_BH3 bonds. The variation of nature of the bonds in terms of ΔE_orb/ΔE_elstat ratio is less pronounced as compared to LB⁺–C_CO2LA⁻ and R–C_CO2R′ bonds.^12a,b

The α-NOCV pair of orbitals, deformation density plot (Δρ₁) and stabilization energy (ΔE_σ) for the charge transfer from the PMe₃CO₂ and NHCCO₂ fragment to the AlH₃ fragment in 1 and 4 are shown in Fig. 3b and d. Fig. 3f gives the plot of deformation density for the interaction of CH₃CO₂⁻ with CH₃⁺ fragment in 9. These plots clearly show depletion of electron density from the O-atom of the CO₂ and the accumulation of the electron density at the Al-atom in 1 and 4 and C-atom in 9. These plots are similar to the typical plot for the donor–acceptor interactions.¹⁸ The ΔE_σ for the _RCO2O⁻ → R′⁺ bond in 7–9 is the highest, followed by the _LBCO2O → B_BH3 bond in 3, 6 and the _LBCO2O → Al_AlH3/AlCl3 bond in 1, 2, 4 and 5 (Fig. 3 and S2†) indicating a stronger σ-interaction in the carboxylic acid and derivatives. Even though, the ΔE_prep for the fragments involved for the _RCO2O⁻ → C_R′⁺ bond formation in 7–9 is higher than those in 1–6, the calculated bond dissociation energies (D_e) for the _RCO2O⁻ → C_R′⁺ bond is also higher in 7–9. This indicates that the acidic character (release of LA) of LBCO₂LA is more than the acidic character (release of H⁺) of carboxylic acid. The experimental report of NHCCO₂ (Scheme 1b)^7a as well as RCO₂(LA)₂ (ref. 7b and c) and LBCO₂(LA)₂ (ref. 5b, c and h) (Scheme 1c) is noteworthy in this regard.

Hence, the EDA-NOCV data suggest that the best bonding description of LBCO₂LA (1–6) can be represented by considering bond formation among LB⁺, CO₂⁻ and LA fragments as in Scheme 3a (Scheme 2b), whereas that of RCO₂R′ (7–9) can be represented by considering bond formation among R, CO₂⁻ and R′⁺ fragments as in Scheme 3b (Scheme 2f). Note that, both EDA-NOCV and NBO charge (Table 1) analysis indicate that the bent CO₂ group in LBCO₂LA and RCO₂R′ can be regarded as having a formal negative charge with the electronic state ²A₁ (1a₂²3b₂²4a₁¹; Fig. 2). This electronic state in the bent CO₂⁻ forces the groups attached to the C-atom to form electron sharing bond and the groups attached to the O-atom to form donor–acceptor bond. As a result, LB⁺ and R group form electron sharing LB⁺–C_CO2LA⁻ bond in LBCO₂LA and R–C_CO2LA bond in RCO₂R′, whereas the LA and R′⁺ group form donor–acceptor _LBCO2O → LA bond in LBCO₂LA and _LBCO2O⁻ → R′⁺ bond in RCO₂R′. Hence, the bent geometry and the electronic state of CO₂ plays a deterministic role towards the bonding interaction with the other groups by altering the usual bonding pattern of LB and R′. Therefore, the CO₂ adduct of LA–LB pair LBCO₂LA can not be classified as space-separated donor–acceptor complexes, rather it can be considered as inorganic analogue of carboxylic acid and its derivatives, RCO₂R′.

Scheme 3 Schematic representation of the bonding interactions of the bent CO₂ fragment with other fragments in (a) LBCO₂LA (1–6) and (b) RCO₂R′ (7–9).

Conclusions

The structure and bonding of the CO₂ adduct of Lewis acid (LA)–Lewis base (LB) pair, LBCO₂LA (LB = PMe₃ and NHC; LA = AlH₃, AlCl₃ and BH₃) and carboxylic acid and its derivatives, RCO₂R′ (R, R′ = alkyl, H) have been analyzed by quantum mechanical calculations at the BP86/TZ2P level of theory. The CO₂ group in LBCO₂LA is significantly bent, which is similar to that of carboxylic acid and derivatives. There is significant enhancement of the electrophilicity and nucleophilicity of bent CO₂ as compared to linear CO₂. However, the enhancement of electrophilicity is higher than the nucleophilicity. The NBO analysis indicates that the direction of charge flow in LBCO₂LA is from LB to LA, whereas the reverse direction of charge flow, R′ to R, is observed for RCO₂R′. The EDA-NOCV data suggest that the bonding interaction of LB with the C-atom of CO₂LA in LBCO₂LA can be best described as 1,2-dipolar LB⁺–C_CO2LA⁻ electron sharing bond. While, the bonding interaction of R with the C-atom of CO₂R′ in RCO₂R′ can be represented as classical electron sharing bond. On the other hand, the bonding interaction of the O-atom of LBCO₂ with LA in LBCO₂LA is a classical donor–acceptor bond. However, the bonding of the O-atom of RCO₂ with R′ in RCO₂R′ can be best represented as 1,2-dipolar _RCO2O⁻ → R′⁺ donor–acceptor interaction. The geometry and the electronic state of bent CO₂ plays a deterministic role towards its bonding with the other groups in LBCO₂LA and RCO₂R′. Therefore, the CO₂ adduct of LA–LB pair, LBCO₂LA, can be considered as inorganic analogue of carboxylic acid and its derivatives, RCO₂R′, although the nature of each type of bonds varied in terms of ratio of orbital to electrostatic contribution (ΔE_orb/ΔE_elstat).

Computational methods

All the geometries were optimized at the gradient-corrected BP86⁹ density functional with the basis set TZ2P.¹⁰ The calculations were performed using ADF 2013.01 package.²² Meta-GGA exchange–correlation functional M06²³ with def2-TZVPP²⁴ basis set was used for the single point calculation on geometries optimized at the BP86/def2-TZVPP level of theory using Gaussian 09 package.²⁵ Natural bond order (NBO)¹⁷ calculations were computed at the same level of theory.

The nature of LB–C bond, O–LA bond, R–C bond and O–R′ bond were investigated by EDA-NOCV analysis at the BP86/TZ2P level of theory using ADF 2013.01 program.²² Scalar relativistic effects were incorporated using Zeroth Order Regular Approximation (ZORA)²⁶ and the core electrons were treated by the frozen-core approximations. Energy Decomposition Analysis (EDA)¹¹ gives the instantaneous interaction energy (ΔE_int) between two fragments in the frozen geometry of the compound. The interaction energy can be divided into three parts:

ΔE_int = ΔE_elstat + ΔE_Pauli + ΔE_orb

ΔE_elstat gives the electrostatic interaction energy between the frozen charge densities of the two fragments. ΔE_Pauli gives the repulsive interaction between two fragments, which are caused by the electrons of same spin. ΔE_orb is the lowering in energy due to the overlap of orbitals of the two fragments. Sum of ΔE_int and ΔE_prep (energy necessary to promote the fragments from their ground state to the geometry and electronic state in the compound) gives −D_e (dissociation energy).

−D_e = ΔE_int + ΔE_prep

EDA-NOCV analysis is an extension of EDA analysis in which ΔE_orb term is decomposed into the contributions from different natural orbitals for chemical valence (NOCV).¹⁸ The EDA-NOCV scheme gives insight to the orbital interactions by providing the energy contributions for each specific orbital interaction between fragments to the total bond energy. The deformation density, Δρ, which is incorporated with bond formation is partitioned into the different components (σ, π and δ) of the chemical bond.

NOCV scheme has been derived from Nalewajski–Mrozek valence theory as eigenvectors that diagonalize the deformation density matrix. The NOCV pairs (Ψ_−k, Ψ_k) decompose the differential density Δρ into NOCV contributions (Δρ_k).

where ν_k and M stand for the NOCV eigen values and the number of basis functions, respectively. Visual inspection of deformation density plots (Δρ_k) helps to determine the symmetry and the direction of charge flow. These density plots also provide the energetic estimations, ΔE_orb^k, for each Δρ_k within EDA-NOCV scheme. In EDA-NOCV method, orbital interaction energy (ΔE_orb) is expressed in terms of NOCV eigen values (ν_k) as
where F^TS_i,i are diagonal Kohn–Sham matrix elements defined over NOCV with respect to the transition state (TS) density (at the midpoint between density of the molecule and the sum of fragment densities). The ΔE_orb^k provide energetic estimation of Δρ_k that may be related to the importance of a particular electron flow channel for the bonding between considered molecular fragments.

Acknowledgements

The authors acknowledge the financial support received from the Department of Science and Technology and INSA-INSPIRE. SD thanks for research grant, no. SR/FT/CS-42/2011 and IFA12-CH-76 for research grant and fellowship. PP thanks for research grant, no. SR/FT/CS-121/2011. IP thanks MHRD for Junior Research Fellowship.

Notes and references

1. (a) A. D. McNaught and A. Wilkinson, Compendium of Chemical Terminology, the “Gold Book”, Blackwell Scientific Publications, IUPAC, Oxford, 2nd edn, 1997; (b) R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1982, 21, 711; (c) T. A. Albright, J. K. Burdett and M.-H. Whangbo, Orbital Interactions in Chemistry, John Wiley & Sons, Inc., New York, 2nd edn, 2013.
2. (a) J. E. Huheey, E. A. Keiter, R. L. Keiter and O. K. Medhi Inorganic chemistry: principles of structure and reactivity, Pearson Education, India, 2006; (b) A. S. Phukan, R. P. Kalagi, S. R. Gadre and E. D. Jemmis, Inorg. Chem., 2004, 43, 5824.
3. (a) E. D. Jemmis, B. V. Prasad, S. Tsuzuki and K. Tanabe, J. Phys. Chem., 1990, 94, 5530; (b) D. Mallick, P. Parameswaran and E. D. Jemmis, J. Phys. Chem. A, 2008, 112, 13080; (c) E. D. Jemmis and P. Parameswaran, Chem.–Eur. J., 2007, 13, 2622; (d) G. Subramanian, E. D. Jemmis and B. V. Prasad, Chem. Phys. Lett., 1994, 217, 296; (e) G. Subramanian and E. D. Jemmis, Chem. Phys. Lett., 1992, 200, 567.
4. (a) K. B. Dillon, F. Mathey and J. F. Nixon Phosphorus: The Carbon Copy, Wiley, Chichester, 1998; (b) F. Mathey, Angew. Chem., Int. Ed., 2003, 42, 1578.
5. (a) C. M. Mömming, E. Otten, G. Kehr, R. Fröhlich, S. Grimme, D. W. Stephan and G. Erker, Angew. Chem., Int. Ed., 2009, 48, 6643; (b) G. Ménard and D. W. Stephan, J. Am. Chem. Soc., 2010, 132, 1796; (c) G. Ménard and D. W. Stephan, Angew. Chem., Int. Ed., 2011, 50, 8396; (d) X. Zhao and D. W. Stephan, Chem. Commun., 2011, 47, 1833; (e) M. J. Sgro, J. Dömer and D. W. Stephan, Chem. Commun., 2012, 48, 7253; (f) C. Appelt, H. Westenberg, F. Bertini, A. W. Ehlers, J. C. Slootweg, K. Lammertsma and W. Uhl, Angew. Chem., Int. Ed., 2011, 50, 3925; (g) R. C. Neu, G. Ménard and D. W. Stephan, Dalton Trans., 2012, 41, 9016; (h) G. Ménard, T. M. Gilbert, J. A. Hatnean, A. Kraft, I. Krossing and D. W. Stephan, Organometallics, 2013, 32, 4416; (i) E. Theuergarten, T. Bannenberg, M. D. Walter, D. Holschumacher, M. Freytag, C. G. Daniliuc, P. G. Jones and M. Tamm, Dalton Trans., 2014, 43, 1651.
6. J. Boudreau, M.-A. Courtemanche and F.-G. Fontaine, Chem. Commun., 2011, 47, 11131.
7. (a) A. Tudose, A. Demonceau and L. Delaude, J. Organomet. Chem., 2006, 691, 5356; (b) B.-H. Xu, R. A. A. Yanez, H. Nakatsuka, M. Kitamura, R. Frçhlich, G. Kehr and G. Erker, Chem.–Asian J., 2012, 7, 1347; (c) A. E. Ashley, A. L. Thompson and D. O'Hare, Angew. Chem., Int. Ed., 2009, 48, 9839; (d) A. Berkefeld, W. E. Piers and M. Parvez, J. Am. Chem. Soc., 2010, 132, 10660.
8. C. Goedecke, R. Sitt and G. Frenking, Inorg. Chem., 2012, 51, 11259.
9. (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822; (c) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406.
10. J. G. Snijders and E. J. Baerends, At. Data Nucl. Data Tables, 1981, 26, 483.
11. (a) K. Morokuma, J. Chem. Phys., 1971, 55, 1236; (b) T. Zeigler and A. Rauk, Inorg. Chem., 1979, 18, 1755; (c) T. Zeigler and A. Rauk, Inorg. Chem., 1979, 18, 1558; (d) M. v. Hopffgarten and G. Frenking, WIREs Comput. Mol. Sci., 2012, 2, 43.
12. (a) G. Frenking, K. Wichmann, N. Fröhlich, C. Loschen, M. Lein, J. Frunzke and V. M. Rayón, Coord. Chem. Rev., 2003, 238–239, 55; (b) G. Frenking, M. Solà and S. F. Vyboishchikov, J. Organomet. Chem., 2005, 690, 6178; (c) A. Krapp, K. K. Pandey and G. Frenking, J. Am. Chem. Soc., 2007, 129, 7596; (d) A. Krapp, F. M. Bickelhaupt and G. Frenking, Chem.–Eur. J., 2006, 12, 9196; (e) A. Krapp and G. Frenking, J. Am. Chem. Soc., 2008, 130, 16646; (f) P. Parameswaran and G. Frenking, Chem.–Eur. J., 2009, 15, 8807; (g) P. Parameswaran and G. Frenking, Chem.–Eur. J., 2009, 15, 8817; (h) G. Frenking, R. Tonner, S. Klein, N. Takagi, T. Shimizu, A. Krapp, K. K. Pandey and P. Parameswaran, Chem. Soc. Rev., 2014, 43, 5106; (i) G. Frenking and F. M. Bickelhaupt in The Chemical Bond: Fundamental Aspects of Chemical Bonding, ed. G. Frenking and S. Shaik, Wiley-VCH Verlag GmbH & Co, Weinheim, Germany, 2014, ch. 4, p. 121.
13. The energy required for the geometrical distortion from linear geometry to singlet bent geometry of CO₂ is 74.0 kcal mol⁻¹ and to triplet bent geometry is 109.4 kcal mol⁻¹ at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory using Gaussian 09 program package. The bent geometry of CO₂ is not a stationary point in the potential energy surface at BP86/TZ2P using ADF2013.01 program package. Hence, we have used the MO energies at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory in Fig. 2.
14. LUMOs are the degenerate antibonding π*-MOs at the M06/def2-SVP level of theory. It is same as the LUMO+1 at the M06/def2-TZVPP//BP86/def2-TZVPP level of theory.
15. W. Petz, C. Kutschera, M. Heitbaum, G. Frenking, R. Tonner and B. Neumüller, Inorg. Chem., 2005, 44, 1263.
16. We have only considered one electron excitation for the fragments.
17. (a) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899; (b) E. D. Glendening, A. E. Reed, J. E. Carpenter and F. WeinholdNBO Version 5.9.
18. (a) M. Mitoraj and A. Michalak, Organometallics, 2007, 26, 6576; (b) M. Mitoraj and A. Michalak, J. Mol. Model., 2007, 13, 347; (c) A. Michalak, M. Mitoraj and T. Zeigler, J. Phys. Chem. A, 2008, 112, 1933; (d) M. Mitoraj and A. Michalak, J. Mol. Model., 2008, 14, 681; (e) M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962; (f) T. A. N. Nguyen and G. Frenking, Chem.–Eur. J., 2012, 18, 12733; (g) M. Mousavi and G. Frenking, Organometallics, 2013, 32, 1743.
19. The conventional use of “→” bond in a donor–acceptor complex (LBLA) indicates donation of a lone pair of electron from LB to the empty orbital of LA (LB → LA). However, if the complex LBLA is described by the zwitterionic form it would yield a formal positive charge on LB and a formal negative charge on LA. The appropriate Lewis structure for LB and LA would then contain singly occupied orbitals, which forms the electron sharing bond (LB⁺–LA⁻). The use of “→” bond and “–” bond have been a point of discussion by Frenking and Krossing. See references: (a) D. Himmel, I. Krossing and A. Schnepf, Angew. Chem., Int. Ed., 2014, 53, 370; (b) G. Frenking, Angew. Chem., Int. Ed., 2014, 53, 6040.
20. The dotted line indicates four π-electrons in the perpendicular plane similar to the bent CO₂ and allylic anion.
21. To confirm the nature of the alcoholic O–R′ bond in ester, 9, we have further carried out EDA-NOCV analysis on CH₃CO₂C₂H₅ (10) and C₂H₅CO₂C₃H₇ (11) as well (Table S5†). The results are consistent with the conclusion drawn for CH₃CO₂CH₃ (9). Hence, the alcoholic O–R′ bonds in the esters 9–11 can be considered as charge separated donor–acceptor RCO₂O⁻ → R′⁺. The comparable values for the ratio ΔE_orb/ΔE_elstat in 9 (0.89), 10 (0.91) and 11 (0.95) indicates similar bonding nature. Hence, the results of compound 9 are only presented in the text.
22. ADF 2013.01, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, http://www.scm.com; G. teVelde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931.
23. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
24. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision B.01), Gaussian, Inc., Wallingford CT, 2010.
26. (a) Ch. Chang, M. Pelissier and Ph. Durand, Phys. Scr., 1986, 34, 394; (b) J.-L. Heully, I. Lindgren, E. Lindroth, S. Lundquist and A.-M. Martensson Pendrill, J. Phys. B: At., Mol. Opt. Phys., 1986, 19, 2799; (c) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597; (d) E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505; (e) E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Int. J. Quantum Chem., 1996, 57, 281; (f) E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142.

---

Footnote

† Electronic supplementary information (ESI) available: It contains the optimized Cartesian coordinates, total bonding energies and EDA-NOCV data for all the molecules. See DOI: 10.1039/c4ra10269j

---