Experimental optimization of a passive planar rhombic micromixer with obstacles for effective mixing in a short channel length†
Iwona Bernacka-Wojcik*a,
Susana Ribeirob,
Pawel Jerzy Wojcika,
Pedro Urbano Alvesa,
Tito Busani‡
a,
Elvira Fortunatoa,
Pedro Viana Baptistac,
José António Covasb,
Hugo Águas*a,
Loic Hilliou*b and
Rodrigo Martinsa
aCENIMAT/I3N, Departamento de Ciência dos Materiais, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa and CEMOP-UNINOVA, Campus de Caparica, 2829-516 Caparica, Portugal. E-mail: ib@uninova.pt; hma@fct.unl.pt; Tel: +351 212948525
bIPC/I3N, Dept. Polymer Engineering, Universidade do Minho, Campus de Azurém, 4800-058 Guimarães, Portugal. E-mail: loic@dep.uminho.pt
cCIGMH, Departamento de Ciências da Vida, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa, Campus de Caparica, 2829-516 Caparica, Portugal
First published on 14th October 2014
Abstract
This paper presents the performance of a passive planar rhombic micromixer with diamond-shaped obstacles and a rectangular contraction between the rhombi. The device was experimentally optimized using water for high mixing efficiency and a low pressure drop over a wide range of Reynolds numbers (Re = 0.1–117.6) by varying geometrical parameters such as the number of rhombi, the distance between obstacles and the contraction width. Due to the large amount of data generated, statistical methods were used to facilitate and improve the results of the analysis. The results revealed a rank of factors influencing mixing efficiency: Reynolds number > number of rhombi > contraction width > inter-obstacles distance. The pressure drop measured after three rhombi depends mainly on Re and inter-obstacle distance. The resulting optimum geometry for the low Re regime has a contraction width of 101 μm and inter-obstacles distance of 93 μm, while for the high Re regime a contraction width of 400 μm and inter-obstacle distance of 121 μm are more appropriate. These mixers enabled 80% mixing efficiency creating a pressure drop of 6.0 Pa at Re = 0.1 and 5.1 × 104 Pa at Re = 117.6, with a mixer length of 2.5 mm. To the authors' knowledge, the developed mixer is one of the shortest planar passive micromixers reported to date.
1. Introduction
Miniaturisation is a recent trend in analytical chemistry and life sciences due to the possibility of performing sophisticated analysis within a device that has a hand hold size, faster sample analysis, higher throughput, portability, and reduced reagent use, all of which are associated with decreased cost. However, physical and chemical surface effects such as capillary forces, surface roughness and chemical interactions of construction materials with reaction processes become more dominant at the micro-scale,1 thus impeding a simple scaling down approach of existing mixing systems. For microfluidic systems, the Reynolds number (Re) is typically smaller than 100 and the flow is considered essentially laminar, which critically limits mixing efficiency.2 Convective mass transfer occurs only in the fluid flow direction and mixing is achieved merely by molecular diffusion. However, diffusion alone is inefficient and imposes the need of long microchannels, meaning that mixing at the micro-scale should be artificially enhanced. Accordingly, two basic principles are exploited to enhance mixing at the micro-scale: active or passive.2 Active mixers depend on an external energy source to achieve mixing, whereas passive mixers solely rely on fluid pumping energy and use special channel designs to restructure the flow, reduce the diffusion length and maximize the contact surface area between fluids.3In contrast to active micromixers or three-dimensional passive micromixers, planar passive micromixers are more cost efficient, can be easily integrated with other microfluidic components and can be fabricated using conventional single layer photolithography techniques. As such, research for achieving the best mixing efficiency in the shortest time and smallest pressure drop using planar passive micromixers has thrived during the last decade. The field is often reviewed.2–5 Table 1 summarizes the main types of existing passive planar micromixers with the corresponding best mixing efficiencies reported to date, relying essentially on chaotic advection to mix water-based fluids with Newtonian behaviour. This table is certainly not a comprehensive review of designs and performance, but its content can serve to appraise mixing efficiencies, pressure drops and mixing distances achieved with innovative micromixer designs. All microchannel designs summarized in Table 1 rely on the split and recombine concept and/or on chaotic advection where obstacles or baffles are inserted along the channel to promote converging and diverging flows. Interestingly, only four out of fourteen designs use curvilinear channels to enhance secondary flows in the curves. Such flows usually result from the elasticity of the fluid rather than from inertial effects; thus, they should be promising in enhancing mixing when viscoelastic fluids, such as polymer solutions, are used.6
| Chip designref. | Mixing length (mm) | Channel width (μm) | Channel depth (μm) | Re range | Best mixing performance (corresponding Re) | Pressure drop in Pa (corresponding Re) | Schematic |
|---|---|---|---|---|---|---|---|
| a Data obtained through simulations. | |||||||
| Y-rectangular mixer7 | 40.0 | 250 | 292 | 10–1000 (1 ml min−1–18 ml min−1) | ∼100% (not available; 8 ml min−1) | ∼9.0 × 104 (not available; 8 ml min−1) |  |
| Rectangular channel with triangle-shaped mixing elements8 | 32.0 | 150 | 50 | 0.1–20.0 | 90% (0.1 and 20) | Not available |  |
| Rhombic (angle 90°) with a converging-diverging element9 | 13.3 | 250 | 130 | 5–200 | 80% (5) 94% (200) | 1.6 × 102 (10)a 5.7 × 103 (200)a |  |
| Rectangular channel with diamond-shaped obstacles10 | 11.0 | 200 | 55 | 0.02–10.00 | 90% (0.1) | 1.5 × 102 (0.1)a |  |
| Curved channels with unbalanced splits and collisions of streams11 | 8.0 | 300 (sum of sub-channels width) | 120 | 10–80 | 64% (80) | Not available |  |
| Rectangular channel with baffles12 | 8.0 | 400 (50–150 for baffle) | 130 | 40–80 | >90% (80) | 3.1 × 104 (80)a |  |
| Labyrinth: “S-shaped” mixers with 180° turns13 | 7.3 | 220 | 267 | 2.5–30.0 | 80% (5) | Not available |  |
| Rhombic (angle 60°) with a converging–diverging element14 | 6.8 | 250 (100 for converging-diverging element) | 130 | 0.1–110.0 | 86% (0.1) 85% (110) | 1.2 × 101 (0.1)a 2.1 × 104 (110)a |  |
| Rhombic (angle 90°) with asymmetrical constriction between rhombi15 | 4.8 | 250 (88–700 for constrictions) | 120 | 1–50 | 90% (20) | 3.6 × 103 (20)a |  |
| C-shape channel with baffles16 | 3.6 | 130 (40 for baffles) | 130 | 1–100 | 85% (81) | 3.4 × 104 (81)a |  |
| Rectangular channel with baffles and gaps17 | 2.4 | 400 (50–150 for gaps) | 120 | 0.1–30.0 | 91% (0.1) 94% (30) | 1.5 × 101 (0.1)a 1.5 × 102 (1)a 1.3 × 104 (40)a |  |
| Modified square wave mixer with by-passes18 | 1.9 per Repeating unit | 200–400 | 200 | Not available (0.1 ml min−1–14 ml min−1) | 87% (not available; 0.2 ml min−1) | 7.0 × 103 per repeating unit (not available; 4.0 ml min−1) |  |
| Rhombic (angle 60°) with branch channels19 | Not available | 250 (100 for branch channels) | 120 | 10–120 | 98% (120) | 9.0 × 103 (120)a |  |
| Rhombic (angle 60°) with diamond-shaped obstacles and rectangular contractions (this paper) | 2.5 | 200 | 130 | 0.1–117.6 | 80% (0.1 and 117.6) | 6.0 (0.1) 5.1 × 104 (117.6) |  |
Ubiquitous to all studies reported in Table 1 is the occurrence of a minimum in mixing efficiency for Reynolds numbers in the range of 1 to 10. This is related to the transition from diffusion to advection driven mixing. Moreover, because all these mixers were optimized using computational fluid dynamics simulations, only the best designs having been fabricated and experimentally tested for mixing efficiency. Only Kashid et al.7 and Goovaerts et al.18 have measured experimentally the pressure drop, whereas the others reported data obtained exclusively from simulations. Although simulations can provide valuable qualitative and quantitative predictions significantly reducing time and cost, it is difficult to access their uncertainty, as the results are affected by the accuracy of modelling, discretization and iteration. For instance, Matsunaga et al.20 have shown that for a T-shaped micromixer operating in the Re range of 140–250, grid-based simulations may overestimate mixing efficiency by up to 30%. Therefore, this work is based exclusively on the experimental characterisation of micromixers. We present a passive planar rhombic micromixer9 with obstructions in the microchannel10 and a contraction placed after each rhombus to further increase interface generation between fluid elements. All these mixing elements (i.e. rhombic channel, obstructions and contractions) enhance mixing through stretching, folding, and break-up processes caused by transverse flows. Rhombic channels induce recirculation at each angle and should also promote curved fluid streams in the rhombus tips. Such curved streams should enhance elastic instabilities and turbulences, and will be further used in a future study focusing on the mixing efficiency and pressure drop optimization for viscoelastic fluids. In addition, a rectangular contraction (called elsewhere “gap”10) is placed after each rhombus to enhance extensional flows, which are known for significantly improving the mixing in viscoelastic fluids.21 The aim of this study is to experimentally optimize the micromixer design by varying geometrical parameters and to identify the most relevant ones for obtaining the best mixing efficiency and shortest mixing length with minimal pressure drop for Newtonian fluids. We investigate the influence of the diamond distance (d) and contraction width (wt) on mixing efficiency and pressure drop over a wide range of flow conditions. For each chip, the total pressure drop and mixing efficiencies at three locations along the channel were measured for twelve Re values ranging from 0.1 to 117.6. Due to the complexity of the study and the number of studied responses, statistical methods were used to facilitate and improve the data analysis.
2. Experimental details
2.1. Fabrication of microfluidic device
The mould for PDMS patterning was fabricated by ultraviolet photolithography in SU-8 2050 (Microchem, USA). The material was spin-coated on silicon wafers at 1530 rpm to form a ∼130 μm thick layer, then soft baked on a levelled hot plate for 5 min at 65 °C and then for 24 min at 95 °C. After cooling (10 min), the samples were UV exposed on a mask aligner (MA6, Suss MicroTec, Germany) for 21 s with an exposure dose of ∼309 mJ cm−2 through an i-line filter (G180336, Suss MicroTec, Germany). Then, the samples were post-baked during 5 min at 65 °C and subsequently for 11 min at 95 °C. Patterns were developed by submersing them in PGMEA (Microchem, USA) for 18 min with magnetic agitation of 500 rpm, rinsing them with IPA and gently drying with compressed nitrogen. The mould was silanized with tridecafluoro-1,1,2,2-tetrahydrooctyl trichlorosilane (Microchem, USA).PDMS (Sylgard 184, Dow Corning, Spain) was prepared by mixing a base and a curing agent in a 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio. The mixture was stirred and degassed in a vacuum desiccator. Afterwards, the PDMS was poured over the SU-8 mould and cured at 100 °C on a levelled hot plate for 3 hours. Then, the PDMS was peeled off from the SU-8 mould.
1 weight ratio. The mixture was stirred and degassed in a vacuum desiccator. Afterwards, the PDMS was poured over the SU-8 mould and cured at 100 °C on a levelled hot plate for 3 hours. Then, the PDMS was peeled off from the SU-8 mould.
The PDMS structures were placed on top of a Petri dish with the negative relief features up. On top of the features of the PDMS structure, an epoxy glue (ES562, Permabond) was poured to form a ∼2 mm thick layer. After ∼72 h degassing in a desiccator, the epoxy glue was cured in an oven at 120 °C for ∼40 min. Then, the cured epoxy was peeled from the PDMS and utilized as a master mould for PDMS soft lithography using the same procedure as described above. The inlets and outlets of the PDMS chips were made using a blunt needle. The chips were irreversibly bonded to glass slides by plasma oxygen (60 s in 13 Pa, 100 W, Plasma electronic Buck Technologien, Germany). After the plasma treatment, the PDMS-glass sandwich was baked at 100 °C for 5 min to increase the bond strength.
The chips were characterized by optical microscopy (Leitz Laborlux 12 ME ST), profilometry (XP-200, Ambios Technology, Inc., Santa Cruz, USA) and scanning electron microscopy (SEM, Zeiss Auriga, Germany).
2.2. Assessment of mixing efficiency
Two fluids were supplied to the microchannels using a syringe pump (Harvard Apparatus PHD 22/200) with two syringes (Hamilton 1005LTN, USA) with 5.0 ml and 2.5 ml capacity. During the experiments, the first syringe was filled with a blue dye (food grade dye, E133) at a 20 times dilution in deionized water, and the 2.5 ml syringe was filled with deionized water only. The two syringes were driven at flow rates ranging from 0.06 ml h−1 (Re = 0.1) to 56.00 ml h−1 (Re = 117.6), measured in separated calibration runs where volumetric flow rates were recorded using gravimetric balances at the micromixers' outlet. The image capturing system consisted of an inverted microscope (Leica DMI 5000M, Leica Microsystems, Germany) connected to a light sensitive CCD camera (Lu160, Lumenera Corporation, USA). Images were processed using ImageJ software to quantify the mixing index and mixing efficiency. The concentration ci at an image point is represented by the pixel intensity value Ii, with the limiting values of concentration cmax and cmin corresponding to Imax and Imin, respectively. Pixel intensity values were normalized according to eqn (1).
 | (1) |
The mixing index (σ) is defined as the standard deviation of the pixel intensity distribution along a line (Fig. 1C) across the micromixer channel:22
 | (2) |
 | (3) |
The Re number was calculated with the following expression:
 | (4) |
2.3. Pressure drop measurements
Pressure drop was measured using a differential pressure transducer (26PC, Honeywell, USA) connected to the pressure taps of the micromixer with flexible Tygon tube (internal diameter 0.8 mm). The transducer voltage output was digitized (NI 9215, National Instruments, USA) and further processed using a home-written LabView routine enabling the on-the-fly oversampling of data, resulting in an increased sensitivity of the transducer.23 The transducer (with tubing) was calibrated using a pressure pump (MFCS-100, Fluigent, France) in the range 7 × 102 to 1 × 105 Pa.2.4. Statistical analysis
Statistical data analysis was performed using JMP 8.01 software (S.A.S. Institute Inc., Cary, NC, USA). Graphical presentations of the models were generated in JMP 8.01 and processed graphically using the OriginPRO 8.5 2010 (OriginLab Corporation, Northampton, MA, USA) diagramming tool. The information to support the developed work can be found in ESI.†3. Results and discussion
3.1. Mixer design and fabrication
The proposed mixer enhances mixing by three means: (i) obstacles within the microchannel, (ii) rhombic channel structure and (iii) contraction in between rhombi (Fig. 1A). The inlet channel of fluid A is split into 2 channels with a width of 200 μm, whereas the inlet and outlet channels of fluid B are 2000 μm long and 400 μm wide. The diameter of inlets and outlet is 1000 μm. In addition, 2 mm away from the inlet B and outlet, pressure taps (diameter: 1000 μm) were placed for measurement of the pressure drop.The presence of obstacles alters the flow direction, inducing recirculation that causes transversal mass transport. Large recirculation is beneficial for increased interfacial contact area between two species, improving diffusion-based and convective mixing. Proper configuration of obstacles is critical, e.g. symmetric obstacles reduce the contact surface leading to lower mixing efficiency than that in the absence of obstacles.24 In general, obstacles are efficient mainly for fast flows (usually at Re above 10), and only optimized geometries (i.e. diamond-shaped10 or asymmetric rectangles25) enable satisfactory mixing at Re below 1. Diamond-shaped obstacles provide better mixing performance than circular- or triangular-shaped obstructions because they split the flow without introducing stagnation areas inside the channel. Furthermore, stepping of the walls of the diamond-shaped obstructions improves mixing efficiencies.10 Therefore, diamond-shaped obstacles (100 μm × 100 μm; width × length) with 20 μm steps were positioned inside a microchannel (200 μm × 125 μm; width × height) with an offset of 30 μm. Because the obstacles occupy the entire depth of the channel, the chip mould can be processed in a single photolithography step. This is of extreme relevance when prototyping and scale up production are concerned.
At very low Re (below 1), micromixers based on diamond-stepped obstacles require a long mixing channel (about 11 mm). A rhombic channel structure was therefore adapted to induce recirculation at rhombus corners.14 When Re is high enough, vortices may be created at the rhombus turns, increasing the advective transport. The average velocity in the rhombic mixer is only half of that in the zigzag mixer, yielding a lower pressure drop. A turning angle of the rhombic mixer of 60° was chosen, as it is the best compromise between mixer footprint, induced dead volume and mixing efficiency.14 The length of the rhombic period is fixed at 1500 μm, whereas the length of the contraction between rhombi is 100 μm.
Once the fluid flows out of the rhombic channel, two streams merge into a single one by means of a contraction and accelerate due to smaller cross-sectional area. After passing the contraction, flow is decelerated and separated into two streams. The added contraction can provide better mixing efficiency at lower Re by an increase of the interfacial area due to stretching and at higher Re by recirculation and vortices.14 Here, a rect-angular contraction was used as this configuration resulted in the shortest mixer length and one of the highest mixing efficiencies reported to date for planar passive mixers17 (Table 1).
To optimize the mixer performance (in terms of a lower pressure drop and shorter length), various mixer configurations were tested, where the controlled variables are the number of rhombi (1, 2 and 3), the width of the contraction between rhombi (wt = 100–400 μm) and the distance between stepped diamond-shaped obstacles (d = 60–140 μm). There were 9 chip configurations of various combinations of wt and d. The mixing efficiency was analysed after each rhombus to evaluate the influence of the number of rhombi.
The micromixers were fabricated in PDMS by a replica moulding technique using a mould produced in SU-8 by UV photolithography.26 SU-8 moulds suffer delamination at the photoresist–substrate interface after fabrication of few PDMS replicas; therefore, we have used an intermediate monolithic epoxy mould to increase the number of possible PDMS replicas from the same SU-8 mould. The moulding process starts with the fabrication of an SU-8 mould, then instead of casting PDMS repeatedly from this mould, PDMS is casted once and used as mould for patterning of an epoxy mould, which can then be used to produce many PDMS replicas without suffering from the delamination problem. The SEM image (Fig. 1B) confirms the good definition of the PDMS features. The PDMS replicas obtained by this process are about 5% smaller than the designed dimensions due to PDMS shrinkage,27 i.e. the obstacle's width is 95 μm instead of the intended 100 μm. Fig. 1B presents also an image of the microfluidic mixer filled with dyes for better visualization.
3.2. Mixing efficiency and mechanism
Fig. 1C displays representative images captured for a micromixer (wt = 250 μm and d = 140 μm) operated at Re = 8.2. At the entrance of the first rhombus, the light grey corresponds to pure water, whereas the darker grey corresponds to the dyed water. As the two fluids flow along the channel, increased mixing is apparent. For each chip, the mixing efficiency in the middle of the first contraction, M(1), second contraction, M(2) and third contraction, M(3) was measured for various Re. Furthermore, M at the outlet channel was measured but no increase was observed, probably due to a short distance (100 μm) from the M(3) access line. To assess the mixing mechanism, images of the micromixers with wt from 100 to 400 μm were compared at various Re. Re of 1.2, 5.9 and 88.2 were chosen to better visualize the fluid behaviour. At Re = 0.1 and Re = 117.6, the fluids at the first contraction are already significantly mixed by means of the obstacles, therefore the grey-scale contrast between fluids is considerably lower. Fig. 2A presents optical microscopy images taken at the first contraction of a micromixer of d = 140 μm, revealing the effect of wt on the flow for various Re. Passing through the contraction, the flow is accelerated and decelerated afterwards. At Re = 1.2 and Re = 5.9, the flow is laminar and mixing is enhanced only by the increased contact between fluids. At the lowest Re (1.2), mixing is better than in the case of Re = 5.9 due to increased residence time. At higher Re (88.2), there is stronger fluid agitation and the flow is greatly affected by the contraction width. At the lowest contraction width (wt = 100 μm), after flowing through the contraction, the water stream is transferred from the inner channel walls towards the outer walls, improving mixing. The flow features were observed for the rectangular contraction by Bhagat et al.10 and can be explained by the formation of vortices. The size of the contraction is critical for the vortices formation at the exit of the contraction; in mixers of d = 140 μm, for wt = 100 μm, vortices are generated starting from Re = 29.4. For wt = 250 μm, vortices are formed only at Re = 117.6, whereas for wt = 400 μm, vortices are not observed in any of the tested flow conditions. Fig. 2B shows a comparison of the vortices generated at Re = 28.4, Re = 58.8 and Re = 117.6 in the mixer with wt = 100 μm and d = 140 μm. The size and intensity of the generated vortices increase significantly with Re enhancing mixing.The effect of d on mixing at Re = 5.9 in mixers with wt = 400 μm is visualized in Fig. 2C. The images indicate that for the mixer with d = 60 μm, water flows mainly next to the channel walls due to small inter-obstacle channel width (i.e. 20 μm; equal to the distance obstacle-channel wall). For d above 100 μm, the inter-obstacle channel width is considerably larger, enabling water to flow in between the obstacles, splitting and recombining the streams with dyed water.
Fig. 3 presents the mixing efficiency (M) of chips of various configurations. In all cases, the dependence between M and Re shows a minimum at Re = 5.9. Below this value, the lower the Re the longer the residence time and the better the mixing by pure diffusion10 (Fig. 2A for comparison of mixing state at Re = 1.2 and Re = 5.9). Above Re = 5.9, the mixing efficiency increases with Re due to the stronger fluid agitation and higher advection. The chip with wt = 400 μm and d = 100 μm shows non-consistent mixing efficiency results, possibly due to fabrication or mixing measurement issues, thus this chip was not taken into account when conducting data analysis.
In order to better understand the mixing mechanism and the role of d, wt and number of rhombi, an efficient mathematical methodology based on statistical techniques was applied for the analysis of the large amount of data displayed in Fig. 3 (Section 3.4).
3.3. Pressure drop
Firstly, the experimental protocol of the pressure drop (dP) measurements was validated by estimating the viscosity of water computed from the pressure drop measured at 28 °C for different flow rates using the mixer that should develop larger pressures (wt = 100 μm, d = 60 μm). This is needed to better match the pressure range that can be measured with the differential pressure transducer. The complex geometry of the developed mixer was simplified into a rectangular channel with length l, height h and width w. The wall shear stress (t) was computed from dP using the following equation:
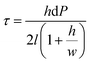 | (5) |
The apparent shear rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app) was computed from the measured volumetric flow Q using the following equation (Newtonian flow):
app) was computed from the measured volumetric flow Q using the following equation (Newtonian flow):
 | (6) |
The inset in Fig. 4A shows the log–log plot of the apparent shear rate as a function of the stress. A power law fitting to the data gives an exponent 1.08 ± 0.07, which indicates a Newtonian behavior,28 confirming that no additional stress build up occurs in the micromixer in spite of the presence of converging and diverging flows. Similar conclusions were reached from dP measurements of water passing in a micron-sized contraction.29 Thus, the approximation of the complex microchannel to a rectangular channel, as proposed by eqn (5), does not bring any error to the dP for the range of flow rates studied here. Accordingly, the stress computed in eqn (5) is error free as long as a correct effective channel width w is used (mentioned below). The true shear rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) is obtained by correcting the apparent shear rate using the following equation:
) is obtained by correcting the apparent shear rate using the following equation:
 | (7) |
The viscosity (η) is then obtained from the Newton relationship:
τ = η![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
| (8) |
Essentially, viscosity data shown in Fig. 4A for the larger shear rates matches the viscosity values measured in separate measurements at 28 °C with a stress-controlled rotational rheometer. At lower shear rates, the shear viscosity shows some scattering due to the limit of sensitivity of the differential pressure transducer. We note that viscosity matching is achieved when an effective channel width of w = 32 μm is used in eqn (5) and (6). Thus, data in Fig. 4A indicate that the micromixer of dimensions wt = 100 μm; d = 60 μm can be used as a large shear rate rheometer for low viscosity liquids, because shear rates as large as 2 × 105 s−1 can be achieved with no inertia instabilities, in contrast to conventional rotational rheometers.
Fig. 4B presents experimental dP results measured after three rhombi for all tested mixer configurations. In general, dP increases linearly with Re; however, for low Re (usually below 12), the pressure drop values were very close to the detection limit of the pressure sensor. Below 2.0 × 103 Pa, dP values are affected by the limit in pressure sensor sensitivity. Thus, a linear regression (intercept 0) of the dP data points measured at larger Re was used to extrapolate the dP for lower Re.
3.4. Statistical analysis of the results
As it can be seen in Fig. 3 and 4, a large amount of data has been generated in this study; therefore, to evaluate influence of the geometric parameters on the device performance for various flow regimes, statistical data treatment was used for the analysis of the results. The Re space was divided in two regions that can be approximated reasonably well by two independent response surface methodology (RSM) models: a low Re regime (from 0.1 to 5.9) and a high Re regime (from 5.9 to 117.6). The analysis was focused on Re = 0.1, which is representative of typical micro-flow conditions10 and also Re = 117.6 for higher throughput applications. The model is fitted using RSM in order to:■ screen for the most important factors influencing the mixing efficiencies and pressure drop;
■ build a mathematical model for all responses under consideration;
■ develop a procedure to identify the most desirable conditions for mixer performance.
When considering all known mathematical models, in which the response surface is continuous over the region being studied, the most suitable in this case seems to be a second-order (quadratic) (M(1), M(2), M(3) and dP) model described in more details in ESI.†
Model improvement for each response was evaluated based on a summary of fit (i.e. the least square regression) parameters summarized in Table S1 in ESI.† The experimental data points were sieved to eliminate those that do not follow the most pronounced trend, probably due to a gross error (details in S1 in ESI†). About 5% of all M data points were eliminated in sieving, increasing the R2 and R2-adj parameters in an average of 0.02. In the case of the dP analysis, the R2 and R2-adj were very high (0.98), therefore no data points were eliminated.
The second-order polynomial responses modelling (quadratic) offered by the RSM appeared to be sufficient for all responses under consideration due to the ability to supply a high coefficient of determination, i.e. R2 = (0.96, 0.96, 0.96, 0.98) and R2 = (0.91, 0.91, 0.91, 0.98) for M(1), M(2), M(3) and dP in low Re and high Re regime, respectively. Such high values of R2, particularly in a low Re regime, indicate good correspondence between the model prediction (fitting) and the experiments, while simultaneously minimizing the overall number of coefficients. The model for each response was validated based on analysis of F-ratio statistics (F-ratio) and the ANOVA probability (Prob > F), indicating accuracy of the models for all responses (details in ESI†).
Fig. 5 presents the results of mathematical fitting to the experimental data points of mixing efficiency (Fig. 5A–C) and pressure drop (Fig. 5D) for Re = 0.1 and Re = 117.6. The mixing efficiency of 80% can be considered as full mixing.30,31
The results indicate that the number of rhombi has the strongest effect on the mixing index; generally, M increases with the number of rhombi, even if after the second rhombus the increase is considerably lower. After the first rhombus (mixer length: 0.9 mm), the mixing efficiency is below 80%, indicating that the fluids are not sufficiently mixed and that additional rhombi are needed (in fact, in the first rhombus the fluids are in contact only in a half of the rhomb, as the other half acts as inlet channel, Fig. 1A). After the second rhombus (mixer length: 2.5 mm), the mixing efficiency is above 80% for all tested configurations. The third rhombus (mixer length: 4.1 mm) would further improve mixing (up to 85% for Re = 117.6), however at the cost of a much longer channel (1.6 mm longer; i.e. 64% longer in the case of two rhombi mixer). Therefore a two rhombi mixer seems to give the best compromise between mixing efficiency and channel length.
At the first contraction, the mixing efficiency varies between 62.5% and 77.5% for the two analysed Re. At Re = 0.1, M(1) is affected mainly by wt; generally, smaller wt gives better mixing, probably due to increased local Reynolds numbers and better contraction–expansion of stream lines. d is less significant for M(1) at Re = 0.1, as the obstacles have usually major effect on mixing for fast flows. d starts playing a more significant role for wt above 250 μm, where higher d values yield a higher M(1). In fact, the images shown in Fig. 2 indicate that in case of d = 60 μm, the hydraulic resistance between obstacles is too high, so the flow develops mainly close to the channel walls. Summarizing, at Re = 0.1 the highest M(1) values are obtained for low wt and low d, whereas the lowest M(1) occurs for high wt and low d. At Re = 117.6, the lowest M(1) is also obtained for regions of high wt and low d, whereas the highest M(1) is observed for high wt and d.
For the same two Re values, M(2) and M(3) vary from 77.5–82.5%, therefore this variation range is very close to the range of uncertainty of the M determination (±6.6%). Most probably, at the second and third contractions, all tested mixer configurations have yielded good mixing and the mixing efficiency saturates. In order to evaluate the effect of geometrical factors on M(2) and M(3), a mixing analysis method of lower uncertainty of the M determination should be used, e.g. based on a fluorescent dye.
In Fig. 5A–C, the effect of the generation of vortices on the mixing state is not visible, as M(1) is measured in the middle of the first contraction (before the vortices are generated, Fig. 2), whereas for M(2) and M(3) the range of mixing efficiency variation is very close to the M uncertainty range. Thus, to measure the effect of the vortices on the mixing state, the mixing efficiency should be measured in more locations along the chip.
The dP results obtained from the mathematical fitting (Fig. 5D) reveal that for Re = 0.1 and Re = 117.6, dP is mainly influenced by the inter-obstacle distance and the effect of wt is barely visible. At Re = 0.1, dP values are comparable with the values reported in previously studied reports (Table 1): it varies from 10 to 138 Pa. The smallest dP are obtained for d between 77 and 125 μm; then, the dP values gradually increase for d values below and above this range. At Re = 117.6, dP is considerably higher than at Re = 0.1: between 4.6 × 104 Pa and 8.6 × 104 Pa. As expected, the closer the obstacles, the higher dP. It should be noted that dP was measured for mixers with three rhombi (length: 4.1 mm), whereas our results indicate that two rhombi mixers (length: 2.5 mm) are sufficient to obtain satisfactory mixing for Newtonian fluids.
The tests of significance of all effects (i.e. factors and interactions) on mixing efficiencies and pressure drop were quantitatively performed using Student's t-test statistics. In general, the model predicts that mixing depends on Re, irrespectively of its value. However, only for M(1) this dependence seems to have a linear character. When considering geometrical factors, wt affects mixing the most, whereas d seems to have a lower but still meaningful effect on the measured responses. Among all factors, Re was found to influence dP the most. This dependence seems to have a linear character. When considering geometrical factors, d nonlinearly affects dP significantly, whereas the role of wt is negligible. The pattern of significance of all factors under consideration is similar for both Re regimes (i.e. significance pattern at low Re is a subset of the significance pattern at high Re).
Response surface maps of experimental regions shown in Fig. 5 facilitate the decision-making process of determining the most appropriate geometry. However, a numerical multi-response optimization enables to find the specific point that maximizes the global desirability, and thus, the optimal performance of the mixer.32 The desirability (i.e. optimization goal, Dn) was defined as maximum values of M(1), M(2) and M(3) and minimum of dP. The contour plots of Dn at low and high Re regimes are shown in Fig. 5. The resulting optimum geometry determined from desirability profiles is described by: wt = 101 μm, d = 93 μm at low Re regime and wt = 400 μm, d = 121 μm at high Re regime.
The above robust optimization deals with an optimization problem, in which the set of feasible solutions are precisely provided for low and high Re regimes. However, as the factors may be uncertain, it is more practical to provide a feasible range of factors, in which desirability is reasonably close to the optimal value. The desirability function for low Re exhibits a broad peak at low wt values and low/medium d values. Therefore, it can be assumed that the uncertainty at the level of 10% in wt and d will still result in robust solution (−1.1% change in Dn). When considering high Re regime, the peak in desirability function is considerably narrower. The uncertainty at the level of 5% in wt and d results in −3.7% change in Dn.
4. Conclusions
To compare the developed micromixer with the state of the art passive planar micromixers reported in Table 1, the mixer length was evaluated, as all the reported mixers give M ≥ 80%, which can be considered as a full mixing.30,31 The developed mixer enables efficient fluid mixing for low (Re = 0.1) and high Re (Re = 117.6) using a channel much shorter (2.5 mm) than that in the majority of planar passive micromixers; only Shih et al.17 have reported a mixer of comparable length (see Table 1). The combination of rhombic channel geometry, diamond-shaped obstacles and rectangular contraction placed after each rhombus has enabled to significantly reduce the mixing length: ∼4× lower than the rectangular mixer with diamond-shaped obstacles (mixing length: 11.0 mm)10 and ∼3× lower than the rhombic (angle 60°) with a converging–diverging element placed after three-rhombi channel (mixing length: 6.8 mm).14To find a compromise, a mixer design should be optimized to obtain high mixing efficiency with a pressure drop as low as possible. As such, in this work the statistical analysis was used to determine mixer configuration that gives the best compromise between those responses. The resulting optimum geometry is wt = 101 μm, d = 93 μm at the low Re regime and wt = 400 μm, d = 121 μm at the high Re regime. For low Re flows, the pressure drop is low enough (6.0 Pa) for the application in lab-on-chip devices, whereas for high Re the mixer imposed relatively large pressure drop (5.1 × 104 Pa). Although, the PDMS chips sealed to glass by oxygen plasma treatment can handle pressures up to 3.4 × 105 Pa,33 i.e. ∼7 times higher than the developed mixer requires at Re = 117.6, a lower pressure drop would be beneficial for the overall device performance and for integration of the mixer with other microfluidic components. Therefore, the developed device enables efficient mixing with a low pressure drop within a very short channel at low Re, making it suitable for applications where several tasks of complex analysis are needed.
Besides, results presented in this paper show that the use of statistical methods can improve significantly the data analysis enabling determination of the most important factors influencing the mixing efficiencies and pressure drop, building a mathematical model for all responses under consideration and identification of the most desirable conditions for mixer performance. Providing details of the statistical analysis (ESI†), we aim to make this efficient mathematical strategy more available to a broader community.
In many microfluidics applications (e.g. inkjet printing; biological analysis), aqueous fluids containing low concentrations of high molecular weight polymers are used.29 Therefore in future work, effect of viscoelasticity on the mixer performance will be studied.
Acknowledgements
This work was supported by the Institute of Nanostructures, Nanomodelling and Nanofabrication, UNINOVA and by FCT-MCTES through CENIMAT/I3N (PEst-C/CTM/LA0025/2013-14) and CIGMH (PEst-OE/SAU/UI0009/2011-14) as well as by the projects EXCL/CTM-NAN/0201/2012, “SMART-EC” FP7-ICT-2009.3.9/258203, PTDC/BBB-IMG/1225/2012, Matepro – Optimizing Materials and Processes (Programa Operacional Regional do Norte (ON.2) NORTE-07-0124-FEDER-000037) and ERC Advanced Grant (INVISIBLE contract number 228144). The authors acknowledge A. C. Vaz for assistance in chip fabrication/characterization and Keep Calm and Publish Papers http://www.keepcalmandpublishpapers.com video blog for graphical guidelines.References
- G. M. Whitesides, Nature, 2006, 442, 368–373 CrossRef CAS PubMed.
- L. Capretto, W. Cheng, M. Hill, X. Zhang and B. Lin, Topics in Current Chemistry, Springer, Berlin, Heidelberg, 2011, pp. 27–68 Search PubMed.
- C.-Y. Lee, C.-L. Chang, Y.-N. Wang and L.-M. Fu, Int. J. Mol. Sci., 2011, 12, 3263–3287 CrossRef CAS PubMed.
- H. Wang, P. Iovenitti, E. Harvey and S. Masood, Smart Mater. Struct., 2002, 11, 662 CrossRef CAS.
- J. S. Kuo and D. T. Chiu, Annu. Rev. Anal. Chem., 2011, 4, 275–296 CrossRef CAS PubMed.
- T. Burghelea, E. Segre, I. Bar-Joseph, A. Groisman and V. Steinberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 066305 CrossRef.
- M. Kashid, A. Renken and L. Kiwi-Minsker, Chem. Eng. J., 2011, 167, 436–443 CrossRef CAS.
- K. Conlisk and G. O'Connor, Microfluid. Nanofluid., 2012, 12, 941–951 CrossRef CAS.
- C. Chung and T. Shih, Microfluid. Nanofluid., 2008, 4, 419–425 CrossRef.
- A. A. S. Bhagat, E. T. K. Peterson and I. Papautsky, J. Micromech. Microeng., 2007, 17, 1017 CrossRef.
- M. A. Ansari, K.-Y. Kim, K. Anwar and S. M. Kim, J. Micromech. Microeng., 2010, 20, 055007 CrossRef.
- C. K. Chung, C. Y. Wu and T. R. Shih, Microsyst. Technol., 2008, 14, 1317–1323 CrossRef CAS.
- P. Li, J. Cogswell and M. Faghri, Sens. Actuators, B, 2012, 174, 126–132 CrossRef CAS.
- C. K. Chung, T. R. Shih, T. C. Chen and B. H. Wu, Biomed. Microdevices, 2008, 10, 739–748 CrossRef CAS PubMed.
- C. K. Chung and T. R. Shih, J. Micromech. Microeng., 2007, 17, 2495 CrossRef.
- R.-T. Tsai and C.-Y. Wu, Biomicrofluidics, 2011, 5, 014103–014113 CrossRef PubMed.
- T. R. Shih and C. K. Chung, Microfluid. Nanofluid., 2008, 5, 175–183 CrossRef CAS.
- R. Goovaerts, W. Smits, G. Desmet, J. Denayer and W. De Malsche, Chem. Eng. J., 2012, 211, 260–269 CrossRef.
- C. K. Chang, T. R. Shih and C. K. Chung, in Nano/Micro Engineered and Molecular Systems (NEMS), 2011 IEEE International Conference on, 2011, pp. 245–248 Search PubMed.
- T. Matsunaga, H.-J. Lee and K. Nishino, Lab Chip, 2013, 13, 1515–1521 RSC.
- Y. C. Lam, H. Y. Gan, N. T. Nguyen and H. Lie, Biomicrofluidics, 2009, 3, 014106 CrossRef CAS PubMed.
- A. D. Stroock, S. K. W. Dertinger, A. Ajdari, I. Mezic, H. A. Stone and G. M. Whitesides, Science, 2002, 295, 647–651 CrossRef CAS PubMed.
- L. Hilliou, D. van Dusschoten, M. Wilhelm, H. Burhin and E. R. Rodger, Rubber Chem. Technol., 2004, 77, 192–200 CrossRef CAS.
- D. Lee and S. H. Lee, J. Korean Phys. Soc., 2008, 52, 580–587 CrossRef.
- A. A. S. Bhagat and I. Papautsky, J. Micromech. Microeng., 2008, 18, 085005 CrossRef.
- I. Bernacka-Wojcik, P. Lopes, A. Catarina Vaz, B. Veigas, P. Jerzy Wojcik, P. Simoes, D. Barata, E. Fortunato, P. Viana Baptista, H. Aguas and R. Martins, Biosens. Bioelectron., 2013, 48, 87–93 CrossRef CAS PubMed.
- S. Lee and S. Lee, Microsyst. Technol., 2008, 14, 205–208 CrossRef CAS.
- N. J. Balmforth, A. Provenzale, N. J. Balmforth and R. V. Craster, in Geomorphological Fluid Mechanics, Springer, Berlin, Heidelberg, 2001, pp. 34–51 Search PubMed.
- L. E. Rodd, T. P. Scott, D. V. Boger, J. J. Cooper-White and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2005, 129, 1 CrossRef CAS.
- H. SadAbadi, M. Packirisamy and R. Wuthrich, RSC Adv., 2013, 3, 7296–7305 RSC.
- N. Tran-Minh, T. Dong and F. Karlsen, Comput. Meth. Programs Biomed., 2013, 117, 20–29 CrossRef PubMed.
- G. Derringer and R. Suich, J. Qual. Tech., 1980, 12, 214–219 Search PubMed.
- J. C. McDonald, D. C. Duffy, J. R. Anderson, D. T. Chiu, H. K. Wu, O. J. A. Schueller and G. M. Whitesides, Electrophoresis, 2000, 21, 27–40 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra10160j |
| ‡ Current address: Electrical and Computer Engineering at University of New Mexico, Albuquerque, NM (USA). |
| This journal is © The Royal Society of Chemistry 2014 |





