Mechanical properties of high-performance elastomeric nanocomposites: a sequential mesoscale simulation approach
Shengwei Denga,
Yongmin Huanga,
Shouhong Xua,
Shaoliang Lin*b,
Honglai Liu*a and
Ying Hua
aState Key Laboratory of Chemical Engineering and Department of Chemistry, East China University of Science and Technology, Shanghai 200237, China. E-mail: hlliu@ecust.edu.cn; Fax: +86 21 64252921; Tel: +86 21 64252921
bSchool of Materials Science and Engineering, East China University of Science and Technology, Shanghai 200237, China. E-mail: slin@ecust.edu.cn
First published on 18th November 2014
Abstract
The incorporation of nanoparticles into elastomeric block copolymers affords engineers an opportunity to obtain polymer nanocomposites that potentially rival the most advanced materials in nature. A computationally efficient simulation method that utilized MesoDyn for the morphologies and the lattice spring model (LSM) for the mechanical properties was adopted in this work. The simulation results show that the selective distribution of nanoparticles in hard or soft segment microdomains of block copolymers will narrow the phase domain size in bicontinuous structures. The Zener model was incorporated into pure elastic LSM to capture the stress relaxation behavior. Mechanical tests reveal that the stress transfer between the polymer matrix and nanoparticles in different composites is critical to the stiffness enhancement. In dispersed structures, adding nanoparticles in a hard microdomain can increase the elastic modulus and maintain high extensibility without impairing its viscosity dramatically. The methods developed in this work yield guidelines for formulating elastomeric nanocomposites with desired macroscopic mechanical responses.
Introduction
Polymer nanocomposites are of wide scientific and commercial interest due to their enhanced properties compared to neat polymers.1–6 Normally, appropriately adding nanoparticles to a polymer matrix can enhance its performance, e.g., high aspect-ratio nanofillers with good dispersion or exfoliation in the polymer result in extremely high stiffness7,8 However, these additives with a homogeneous distribution in the polymer matrix may also have adverse effects. These nanocomposites are usually stiff but inextensible, like ceramic, or extensible but soft, like rubber.9 Selectively reinforcing certain domains of phase-separated block copolymers with inorganic nanoparticles would be a proper way to achieve unprecedented improvements in stiffness and strength without losses in the extensibility of the composites.10,11 Gareth and co-workers12 used a two-solvent processing approach to obtain the high-performance material based on hard-soft block copolymers (Elasthane). The nanofillers distributed in the hard phase gave rise to a dramatic increase in stiffness of up to 23-fold and a concurrent improvement in strength, while the extensibility was maintained which was determined by unreinforced soft phase.Inspired by high-performance Elasthane nanocomposites, hard-soft block copolymers with bicontinuous and dispersed structures are utilized as model systems, and nanoparticles are dispersed into the hard phase, soft phase or interface by varying the interaction between the nanoparticle and polymer. Thermodynamic or kinetic barriers may inhibit the selective dispersal of nanoparticles in polymer matrices, e.g. hydrophilic nanoparticles in hydrophobic polymer microdomains. Fortunately, recent experiments12 showed that it is possible to overcome this obstacle by advanced experimental techniques. Comparing with mature experimental techniques, only a few simulation works correlate the structure and mechanical behaviour of this kind of high-performance materials.13 Due to the complexity of polymer nanocomposites, the main challenge for simulating the mechanical properties is the restriction by the computing capability, and an effective simulation method with wide applicability is favourable. Based on our previous works,14,15 a computationally efficient method (sequential mesoscopic simulation) was adopted in this work to capture mechanical responses such as the stiffness, fracture strain and stress relaxation. This method utilized MesoDyn simulation16–18 for structures and lattice spring model (LSM) for mechanical properties. Subsequently, the pure elastic model was replaced by an anelastic solid model (Zener model) in LSM to study the viscoelastic behavior.
In order to obtain morphologies of different composites, atomic simulations provide the first opportunity in sight to reach the most precise model.19 In this work, a huge number of nanoparticles should be modelled efficiently, and then the discrete positions of particles inevitably need to be replaced by a cruder description.20,21 Field-based approaches are more suitable for obtaining the structure evolution information comparing to atomic simulations which are computationally expensive. Therefore, dynamic density functional theory embodied in MesoDyn was adopted to simulate the meso-structures.22
LSM is a discretized method for continuum elastic media and often used to simulate deformation and fracture of complicated structural systems. For more details related to LSM, see ref. 23–26. An important part of this work is the incorporation of linear viscoelastic model into pure elastic LSM. In many cases, elastic constitutive model works well when time dependent effect can be neglected. Otherwise, more appropriate constitutive model is needed to describe the mechanical behavior. Time dependent effect indicates that the stress–strain behavior of materials changes with the time. Monette et al.27 investigated the mechanical properties of short-fiber polymer composites by a two-dimensional triangular lattice, which described the viscoelastic behavior through the incorporation of Maxwell units. Buxton et al.28 studied the viscous deformation of homopolymers containing various shapes of nanofillers by LSM. In this work, a similar approach based on Monette and Buxton's work was adopted to capture the stress relaxation behavior of different multi-component composites, which especially focused on the influence of selective dispersal of nanoparticles on the viscous deformation.
Model and simulation method
The sequential simulation method combines the MesoDyn simulation for nanocomposite morphologies with the pure elastic or viscoelastic LSM for mechanical properties. The output of the former serves as the input of the latter.A. MesoDyn simulation
The structural evolution of block copolymer and its nanocomposites was simulated by using the MesoDyn program incorporated in the Materials Studio, version 5.5, from Accelrys. MesoDyn method is based on the dynamic mean-field density functional theory, in which the dynamics of phase separation can be described by Langevin equations to study the diffusion of the density field. There is a one-to-one relationship between the density distribution function of the system and the external potential field. The free energy F of an inhomogeneous liquid is a function of density field ρ(r), and all thermodynamic functions can be derived from the free energy. The polymer chains are modelled as ideal independent Gaussian chains consisting of beads and a mean-field non-ideal contribution. The chain topology depends on the coarsening degree of the original system. On a coarse-grained time scale, a probability Ψ can be assigned to a certain configuration of bead positions, correspondingly, a free energy functional F[Ψ] can be constructed. Taking conditional minimum, the undetermined multiplier UI is just the external potential, then the density functional of the free energy can be obtained as:
 | (1) |
 | (2) |
The intrinsic chemical potentials can be derived by functional differentiation of the free energy, µI(r) = δF/δρI(r).
On the basis of these equations, the generalized time-dependent Ginzburg–Landau theory can be established. The time dependence is described by a diffusion equation. The Langevin equations for the diffusion dynamics of the density fields are then given by:
 | (3) |
 | (4) |
| 〈η(r,t)〉 = 0 | (5) |
| 〈η(r,t)η(r′,t′)〉 = −2MvBβ−1δ(t − t′)∇rδ(r − r′)ρAρB∇r′ | (6) |
The kinetic coefficient MvBρAρB models a local exchange mechanism. The Langevin equations are constructed for an incompressible system with dynamic constraints:
 | (7) |
B. Lattice spring model for simulating elastic deformation and fracture
Born LSM is a numerical technique for discretizing the linear elasticity theory, and it is frequently used to simulate deformation and fracture of materials. The material is represented by a network of springs, which occupy the nearest and next nearest neighbour bonds of a simple cubic lattice. Although lack of rotational invariance, in the systems considered here, rotations are assumed to be small, and therefore a Born spring model is implemented. By assigning different force constants according to the composition of different nodes, the model is successful in the study of heterogeneous systems. Typically, the lattice spring model allows us to determine micromechanical properties in a computationally efficient way.The energy associated with a node m in the cubic lattice is taken to be of the form:23
 | (8) |
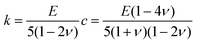 | (9) |
The elastic force acting on the mth node is a linear function of the displacement because of the harmonic form of energy in eqn (8). The force acting on the mth node, due to the local displacement of the spring between nodes m and all neighboring n, is given by.
 | (10) |
If the external forces are applied to the boundary nodes with the spring constants specified, the constraint that all these linear forces must balance at each node at equilibrium results in a set of sparse linear equations. The solution of these equations is obtained by using a conjugate gradient method to find the equilibrium configuration corresponding to the situation without net force at each node. The stress and strain tensors are calculated by the forces and displacements. The average strain and the applied stress can then be used to calculate the Young's modulus (stiffness) which is defined as the stress of a material divided by its strain.
The critical fracture strain is a measure of the extensibility of the material which corresponds to the maximum strain that the system can sustain before happening catastrophic failure. In order to obtain the fracture strain of different polymer materials, here we adopt a probabilistic method, which indicates that a fracture is considered to be formed with a probability proportional to the local stress. To determine when the fracture surface is to be created, a rate of failure ps(t) of a surface s at time t is introduced as follows:
 | (11) |
 | (12) |
To initiate fracture, a constant strain rate is applied to the sample with periodic boundary condition adopted. The strain is varied in a predetermined range by a golden section method to find the crack tip (the strain error is less than 0.1%). An initial time step Δt0 is introduced; the fracture occurs if the average time interval is smaller than Δt0. After the beginning of the fracture, the applied strain rate will be increased at each iteration by a constant (here we choose 0.001). Therefore, the creation of fracture surfaces depends on the correct probability weightings in eqn (11), and the relaxation of material surrounding the propagating crack tip takes the average time interval over which the crack grows into consideration. In this manner, the deformation and fracture cease at the fracture point when the stress no longer increases with the increase of strain, and the strain and stress at this point correspond to the fracture strain and tensile strength, respectively. More detailed description about the fracture process can be found in our previous work.14,29
C. Viscoelastic LSM for studying stress relaxation
The spring between nodes in LSM was replaced by a viscoelastic model to capture the stress relaxation behaviour of different composites. In pure elastic LSM, the strain applied to the system boundaries increases by a constant at each time step, which enables the system to evolve through a series of equilibrium states. The time step is not related to the real time. In viscoelastic LSM, a time frame is introduced through the incorporation of viscous deformation in each iteration. The equilibrium bond lengths are no longer constant, but time dependent, which incorporates viscous deformations related to the viscosity of different components. Similarly, the plasticity can also be incorporated into LSM, force constants will update in each iteration according to plastic model, while the plastic behaviour is beyond the research scope of this paper.As shown in Fig. 1, an anelastic solid model (Zener model) is considered in this work to replace the previous pure elastic model. This model consists of a Kelvin unit in series with an elastic unit (spring), and it is often used to describe creep and stress relaxation behaviors.
 | ||
| Fig. 1 The anelastic solid model composed of a Kelvin unit (a spring of modulus E in parallel with a dashpot of viscosity η) in series with a spring of modulus E. | ||
For simplicity, springs in the model use the same sprint constant, and this treatment is enough to provide a reasonable adjustment range of stress relaxation. The stress can be reduced by half if time approached infinity, the degree of stress relaxation is influenced by the strain rate and viscosity. When a constant uniaxial stress σ0 is applied to a homogeneous system, the response function is given by:
 | (13) |
 | (14) |
The viscous strain at t + Δt is of the form,
| uvmn(t + Δt) = uvmn(t) + Δt(Mmnumn − Mvmnuvmn)Vvmn | (15) |
Results and discussion
A. Morphology
The microphase separations of diblock copolymer and its nanocomposites were studied by MesoDyn. An elastomeric block copolymer is considered in this work, such as thermoplastic polyurethane elastomers. This kind of polymer is composed of hard segments (H) and soft segments (S). The thermodynamic incompatibility of H and S drives the polymer system into a two-phase morphology. The incorporation of nanoparticles (N) into the elastomeric block copolymer is also performed by MesoDyn. As for thermodynamic incompatibility system, the morphology of block copolymer is strongly related to chain structures such as block sequence, block ratio, block length, and chain architecture. It means that different meso-structures can be obtained by specifying different chemical natures of the system. Bicontinuous and dispersed (hard segment disperse in soft segment matrix) structures were considered in this work.In MesoDyn simulations, two sets of parameters should be defined: one is the chain topology in terms of repeat segments (or beads), and the other is the interaction energy between different components. Table 1 shows the Gaussian chain parameters for 12 typical polymer materials investigated in this work. Generally, two components are thermodynamically incompatible when the interaction parameter (repulsion) χ between them is larger than 0.5. The model systems here are based on PS-b-PAN block copolymer systems (PS: polystyrene; PAN: polyacrylonitrile). And the MesoDyn input parameter between H and S is 4.75. More simulation details about the structure evolution of this system can be found in ref. 30. The nanoparticles was simply treated as a chain with chain length of 1, and hence the distribution of nanoparticles in polymer matrix is controlled by varying the interaction parameter between nanoparticles (N) and H or S. In this work, we choose χN,H = 4.75, χN,S = 0 for the systems that particles selectively disperse in the soft phase (χN,H represents the interaction parameter between N and H); χN,H = 0, χN,S = 4.75 for the systems that particles selectively disperse in the hard phase; and χN,H = 4.75, χN,S = 4.75 for the systems that particles selectively disperse in the interface.
| Polymer materials bicontinuous structure | Gaussian chain | Polymer materials dispersed structure | Gaussian chain |
|---|---|---|---|
| a B-1 & D-1: diblock copolymer; B-2 & D-2: diblock copolymer with nanoparticles selectively dispersed in hard phase; B-3 & D-3: diblock copolymer with nanoparticles selectively dispersed in soft phase; B-4 & D-4: diblock copolymer with nanoparticles selectively dispersed in the interface between hard and soft phases; B-5 & D-5: triblock copolymer with nanoparticles selectively dispersed in hard phase; B-6 & D-6: triblock copolymer with nanoparticles selectively dispersed in soft phase. | |||
| B-1 | S25–H25 | D-1 | H5–S28 |
| B-2 | S25–H25; N1 | D-2 | H5–S28; N1 |
| B-3 | S25–H25; N1 | D-3 | H5–S28; N1 |
| B-4 | S25–H25; N1 | D-4 | H5–S28; N1 |
| B-5 | H12–S25–H13; N1 | D-5 | S14–H5–S14; N1 |
| B-6 | H12–S25–H13; N1 | D-6 | S14–H5–S14; N1 |
All MesoDyn simulations were carried out in a cubic grid with 30 × 30 × 30 cells of mesh size. The grid parameter λ ≡ γµ−1 = 1.1543, where γ presents bond length, and µ is the mesh size. The compressibility parameter is equal to 10kT, and the total simulation time is 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps without shear. The noise parameter Ω ≡ V−1µ3 = 100. The time step is 50 ns. The simulations are performed at ambient temperature 298 K. The relative concentration of nanoparticles in all systems which contain nanoparticles is equal to 2%. Note that the block copolymer is composed of hard segments and soft segments, so the relative concentration of hard or soft segments is related to the Gaussian chain topology. Table 1 shows that bead numbers of hard or soft segments in Gaussian chain are the same in all bicontinuous structure systems, it means the concentration of hard phase is equal to that of soft phase in the system.
000 steps without shear. The noise parameter Ω ≡ V−1µ3 = 100. The time step is 50 ns. The simulations are performed at ambient temperature 298 K. The relative concentration of nanoparticles in all systems which contain nanoparticles is equal to 2%. Note that the block copolymer is composed of hard segments and soft segments, so the relative concentration of hard or soft segments is related to the Gaussian chain topology. Table 1 shows that bead numbers of hard or soft segments in Gaussian chain are the same in all bicontinuous structure systems, it means the concentration of hard phase is equal to that of soft phase in the system.
Fig. 2 shows the dispersed morphology of different polymer materials. The system (a) without nanoparticles shows that the hard phase is spherically dispersed in the soft phase matrix. For system (b), the nanoparticles mainly concentrate in the hard phase due to the lower repulsion energy between beads N and H. In system (c) and system (d), the nanoparticles mainly concentrate in the soft phase and interface, respectively. System (e) is similar to system (b), and system (f) is similar to system (c). It can be seen that the phase domain size becomes smaller by varying the polymer chain architecture from diblock to triblock copolymer. However, the chain sequence does not impact the phase separation structure (all are dispersed morphology) in this work.
Interfacial area between different phases is an important parameter related to the mechanical properties. The total interfacial area is defined as S = Nx + Ny + Nz, where Nx, Ny and Nz are the numbers of interfacial bonds in the x, y and z directions, respectively. The total density data for each grid from the MesoDyn should be normalized to 1. Here we take two adjacent grids (grid a and b) in the x direction for example. The influence of nanoparticles in this system is ignored due to the small amount, and the number of interfacial bonds in the x direction between grid a and b is given by:
| Iab = min(ρaPS +ρbPS, ρaPP + ρbPP) | (16) |
Fig. 3 shows the total interfacial area of different systems when the order parameter reaches the equilibrium value. First we focus on the dispersed structures shown by orange belts (right side) in the figure. The addition of a small amount of nanoparticles has slight impact on the interfacial area, while the area increases by about 30% in triblock nanocomposites shown in the last two systems. It elucidates that the phase domain size in triblock copolymer is smaller than that in diblock copolymer. In bicontinuous structure systems, we can find a similar phenomenon that triblock nanocomposites have relatively high interfacial areas. Notably, B-2 and B-3 systems have higher interfacial areas comparing to B-1 and B-4, it means that the selective dispersal of nanoparticles in hard or soft segments narrows the phase domain size in bicontinuous structures. Actually, the incorporation of nanoparticles into polymer blends has attracted considerable attention for decades31 because the nanoparticles can be used to control the morphology of polymer blends,32,33 act as the compatibilizer for immiscible polymer blends,34,35 e.g. the incorporation of SiO2 in immiscible polypropylene (PP)/polyolefin elastomer (POE) blends lead to a much finer morphology.36
B. Mechanical properties: stiffness, fracture strain and stress relaxation
| km = ρHkH + ρSkS + ρNkN | (17) |
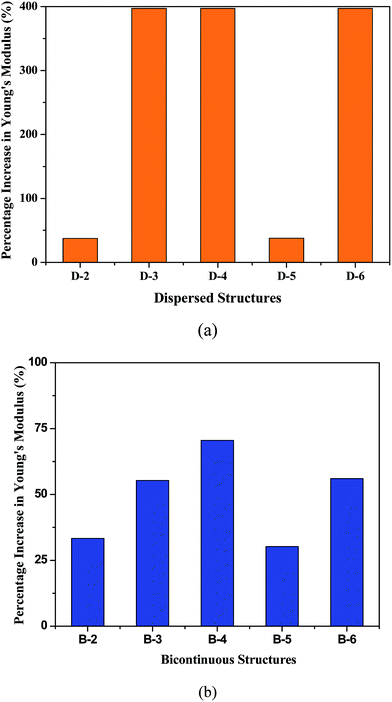
The relative concentration of nanoparticles in all nanocomposites is 2%. Note that filler loading and morphologies have strong impacts on the final mechanical responses,28,37 the system considered in this work is treated as nanocomposites with solid spheres reinforcing nanofillers. In Fig. 4, we plot the percentage increase in Young's modulus of different polymer nanocomposites comparing to pure diblock copolymer. As shown in Fig. 4a, the dispersed structure system with nanoparticles distributed in the interface (D-4) or soft phase (D-3) has a high Young's modulus, the addition of 2% nanoparticles can make the stiffness increase about 400%. The Young's modulus of D-2 system that contains nanoparticles in hard phases increases by about 40%, which is one tenth of that in D-3 system. It proves that nanoparticles distributed in soft segments are much more efficient to enhance the stiffness than that dispersed in hard segments in dispersed structure systems. The same phenomenon can be found in D-5 and D-6 systems, for the reason that the stiffness is mainly controlled by the soft segment matrix. The Young's modulus increments in D-5 and D-6 systems are similar to those in D-2 and D-3 systems, respectively. It elucidates that reducing the phase domain size has slight influence on the percentage increase of stiffness. Fig. 4b shows the percentage increase of stiffness in bicontinuous structures. Similar to dispersed structure systems, the system with nanoparticles distributed in the interface (central column) is effective for the enhancement of Young's modulus, the stiffness increases by about 1.7 times with the addition of 2% nanoparticles. The increment of Young's modulus in B-3 system reaches to 150%, and the increment of Young's modulus in B-2 system is about 70%. The stiffness enhancement of systems with nanoparticles dispersed in soft phase (B-3 or B-6) is not as strong as that in dispersed systems (D-3 or D-6). The reason for this phenomenon is as follows. Unlike dispersed structures, the hard phase form a network in bicontinuous structures and control the stiffness, adding nanoparticles into soft phase lead to the stiffness in turn controlled by the enhanced soft phase, this will impair the enhancement efficiency in some way. In bicontinuous structures, the percentage increase in Young's modulus is comparing with the stiffness of hard segment phase instead of soft segment phase in dispersed structures. Besides, the stress concentration is easy to be alleviated by the softer phase in bicontinuous structures. From the results of B-5 and B-6 systems, reducing the phase domain size also hardly influence the enhancement of stiffness. Notably, the crystallization in polyurethane will influence the distribution of fillers in various ways due to several factors including the properties of fillers.12,38 But the crystallization process is related to chain structures with regular arrangement, which cannot be studied directly by the mesocopic simulation method. Similar to the Laponite reinforced polyurethane12 where the Laponite forms a jammed structure in crystalline hard domain, the nanoparticle reinforcing effect are modeled by its density filed in LSM.
Fig. 5 shows the critical fracture strain of different nanocomposites with dispersed and bicontinuous structures separately. Note that the fracture strain of pure polymer system in dispersed structures (D-1) is much lower than its counterpart in bicontinuous structures (B-1) under the same situation. As can be seen in Fig. 5a, dispersing nanoparticles into hard phase (D-2 and D-5 systems) is efficient to maintain the extensibility, especially comparing to the systems with nanoparticles dispersed in soft phase (D-3 and D-6 systems). These results show a good agreement with the existing experiments.39 By analyzing the fracture position, we find that the fracture mainly occurs in hard phase or enhanced soft phase. The extensibility is controlled by unreinforced soft segment phase in elastomeric nanocomposites, adding nanoparticles in soft segment phase will increase the total stiffness, but impair the extensibility significantly. In Fig. 5b, systems with nanoparticles dispersed in hard phase (B-2 and B-5 systems) can maintain high fracture strain (about 0.96%). While the critical fracture strain of systems with nanoparticles dispersed in soft phase (B-3 and B-6 systems) decrease by about 25%. Similarly, in polyurethane elastomer nanocomposites, nanocellulose crystals covalently bonded and specifically associated with the hard microdomains, which yields ultrahigh tensile strength and stain-to-failure.11 Reducing phase domain size lead to a slight increase of the critical fracture strain in both bicontinuous and dispersed structure systems.29 And the extensibility is severely impaired by the dispersal of nanoparticles in the interface (B-3 and D-3 systems). We conclude from the above analysis that adding nanoparticles in hard phase of diblock copolymer elastomers yield the stiff polymer nanocomposites with high extensibility.
In order to evaluate the stress relaxation, the percentage decrease in Young's modulus is considered as a function of time in Fig. 6. The pure elastic line is obtained by pure elastic LSM for comparison. The Young's modulus for other systems deviate from the pure elastic line (straight line) due to the viscous deformation. The distribution of nanoparticles has a significant impact on the stress relaxation. Viscous deformations result in a reduction of the reinforcement efficiency. As for dispersed structures, Fig. 6a shows that the stress of diblock copolymer without nanoparticles (D-1 system) decreases by about 25% after 100 time steps, and the stress of system with nanoparticles distributed in the hard phase decreases by about 22%. However the stresses of D-3 and D-4 system decrease only by about 4% after 100 time steps. It elucidates that the viscous deformations are mainly controlled by the soft phase with the lowest viscosity, and adding nanoparticles into polymer will impair its viscosity. In Fig. 6b the decrease amplitude of stress in bicontinuous systems is smaller than that in dispersed systems. The Young's modulus was controlled by the hard phase framework, and hence the dispersion of nanoparticles in hard phase will also impair the stress relaxation dramatically. The stress relaxation also appears to be severely impaired in systems with nanoparticles dispersed in the interphase or soft phase. In experiment, the tensile strain rate is usually quite low and the stress relaxation defers the fracture or break process. According to the time-temperature equivalence principle, the increase of relaxation time often corresponds to the increase of temperature.42
 | ||
| Fig. 6 The percentage increase in effective Young's modulus as a function of time for different polymer nanocomposites. (a) Dispersed systems and (b) bicontinuous systems. | ||
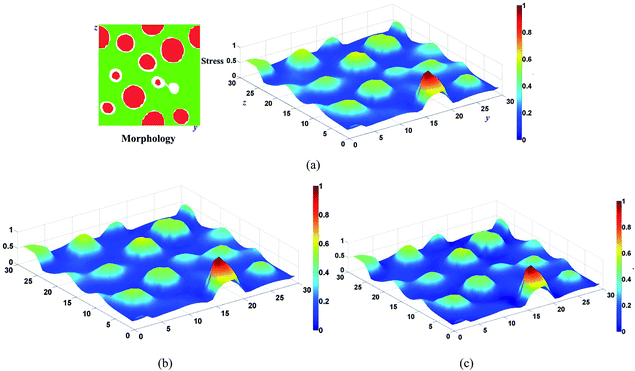
In order to show the stress relaxation behavior clearly, we choose a typical system (D-1 in Fig. 6a) to show this process. Fig. 7 depicts the normal stress field for a dispersed structure diblock copolymer, where the hard phase is dispersed in soft matrix. The tensile is applied in x direction and the morphology are shown in the right upper corner, where the soft and hard phases are denoted with red (dark) and green (grey), respectively. It can be seen that the stress distribution is similar to the morphology, and the hard phase loads higher stress due to the larger stiffness. The viscosity of soft phase is much lower than that of hard phase. Comparing Fig. 7a with 7b, we can find a clear reduction of the average stress in soft phase after 40 time steps. With the relaxation time goes on, the stress further relaxed (Fig. 7c). Note that the relaxation time considered here is not enough for the stress release in hard phase due to the high viscosity, but the average stress in hard phase is slightly reduced due to the stress transfer from the hard phase to soft phase.
Conclusions
In this paper, mesostructures of elastomeric nanocomposites and macroscospic mechanical properties were correlated by sequential mesoscopic simulation method, this method utilized MesoDyn for morphologies and LSM for mechanical responses. From the morphology result, the phase domain size became smaller by varying the polymer chain architecture from diblock to triblock copolymer. And the selective distribution of nanoparticles in hard or soft segments narrowed the phase domain size in bicontinuous structure systems.36 The output of MesoDyn served as the input of pure elastic LSM. Simulation results showed that adding nanoparticles in polymer matrices resulted in a higher Young's modulus, and nanoparticles distributed in soft phase were more efficient to enhance the stiffness than that dispersed in hard phase. In bicontinuous structures, the hard phase formed a stiff network and controlled the stress, while in dispersed structures, the soft phase sustained the deformation and stress was hard to transfer from the soft phase to hard phase. Selective dispersion of nanoparticles in these two structures would change the stress transfer process and led to different efficiencies of stiffness enhancement. Further studies were focusing on the critical fracture strain. Adding nanoparticles in soft phase impaired the extensibility dramatically, while nanoparticles dispersed in hard phase increased the elastic modulus without loss of high extensibility. These results agreed well with experimental observations.12 In viscoelastic LSM, our calculations showed that the viscous deformations are mainly controlled by the soft phase with the lowest viscosity and adding nanoparticles into soft segments would impair its viscosity significantly.40 It elucidated that dispersing nanoparticles into hard phase was a reasonable way to design high-performance elastomeric nanocomposites.Through the integration of a morphological model and a micromechanical model we have related the mechanical response of complex polymer nanocomposites without large-scale computations. The predictive capabilities of such an integrated approach can aid in the design of new materials. Rate (time)-dependent deformation behaviour is often observed in solid polymers. We have studied the stress relaxation by viscoelastic LSM, the viscous flow within the matrix was found to reduce the stress concentrations. The relation between the strain-rate and fracture process is not elucidated in this work, a feasible way is to combine probabilistic LSM and viscoelastic model, which is expected to complement more traditional mechanisms such as ductile breaking.
Acknowledgements
Financial support for this work was provided by the National Natural Science Foundation of China (no. 91334203), the 111 Project of Ministry of Education of China (Grant B08021) and the Fundamental Research Funds for the central Universities of China.Notes and references
- A. C. Balazs, T. Emrick and T. P. Russell, Science, 2006, 314, 1107–1110 CrossRef CAS PubMed.
- H. Zou, S. Wu and J. Shen, Chem. Rev., 2008, 108, 3893–3957 CrossRef CAS PubMed.
- C. Chevigny, N. Jouault, F. Dalmas, F. Boué and J. Jestin, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 781–791 CrossRef CAS.
- V. Baheti, J. Militky and M. Marsalkova, Polym. Compos., 2013, 34, 2133–2141 CrossRef CAS.
- I. U. Unalan, G. Cerri, E. Marcuzzo, C. A. Cozzolino and S. Farris, RSC Adv., 2014, 4, 29393–29428 RSC.
- J. Zhu, M. Chen, Q. He, L. Shao, S. Wei and Z. Guo, RSC Adv., 2013, 3, 22790–22824 RSC.
- S. Stankovich, D. A. Dikin, G. H. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Nature, 2006, 442, 282–286 CrossRef CAS PubMed.
- F. He, S. Lau, H. L. Chan and J. Fan, Adv. Mater., 2009, 21, 710–715 CrossRef CAS.
- M. Moniruzzaman and K. I. Winey, Macromolecules, 2006, 39, 5194–5205 CrossRef CAS.
- U. Khan, P. May, A. O'Neill, J. J. Vilatela, A. H. Windle and J. N. Coleman, Small, 2011, 7, 1579–1586 CrossRef CAS PubMed.
- A. Pei, J.-M. Malho, J. Ruokolainen, Q. Zhou and L. A. Berglund, Macromolecules, 2011, 44, 4422–4427 CrossRef CAS.
- S. M. Liff, N. Kumar and G. H. McKinley, Nat. Mater., 2006, 6, 76–83 CrossRef PubMed.
- T. M. Madkour, F. M. Hagag, W. Mamdouh and R. A. Azzam, Polymer, 2012, 53, 5788–5797 CrossRef CAS PubMed.
- S. Deng, X. Zhao, Y. Huang, X. Han, H. Liu and Y. Hu, Polymer, 2011, 52, 5681–5694 CrossRef CAS PubMed.
- X. Zhao, S. Deng, Y. Huang, H. Liu and Y. Hu, Chin. J. Chem. Eng., 2011, 19, 549–557 CrossRef CAS.
- B. Van Vlimmeren and J. Fraaije, Comput. Phys. Commun., 1996, 99, 21–28 CrossRef CAS.
- B. Van Vlimmeren, M. Postma, P. Huetz, A. Brisson and J. Fraaije, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 5836 CrossRef CAS.
- B. Van Vlimmeren, N. Maurits, A. Zvelindovsky, G. Sevink and J. Fraaije, Macromolecules, 1999, 32, 646–656 CrossRef CAS.
- K. M. Langner and G. Sevink, Soft Matter, 2012, 8, 5102–5118 RSC.
- G. Allegra, G. Raos and M. Vacatello, Prog. Polym. Sci., 2008, 33, 683–731 CrossRef CAS PubMed.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423 CrossRef CAS PubMed.
- H. Chen, Y. Wu, Y. Tan, X. Li, Y. Qian and H. Xi, Eur. Polym. J., 2012, 48, 1892–1900 CrossRef CAS PubMed.
- G. A. Buxton, C. M. Care and D. J. Cleaver, Modell. Simul. Mater. Sci. Eng., 2001, 9, 485 CrossRef.
- G. A. Buxton and A. C. Balazs, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 054101 CrossRef.
- G. A. Buxton and A. C. Balazs, Macromolecules, 2005, 38, 488–500 CrossRef CAS.
- L.-T. Yan, E. Maresov, G. A. Buxton and A. C. Balazs, Soft Matter, 2011, 7, 595–607 RSC.
- L. Monette, M. Anderson and G. Grest, Polym. Compos., 1993, 14, 101–115 CrossRef CAS.
- G. A. Buxton and A. C. Balazs, J. Chem. Phys., 2002, 117, 7649–7658 CrossRef CAS PubMed.
- S. Deng, Y. Huang, C. Lian, S. Xu, H. Liu and S. Lin, Polymer, 2014, 55, 4776–4785 CrossRef CAS PubMed.
- S. Piotto, S. Concilio, F. Mavelli and P. Iannelli, in Macromolecular symposia, Wiley Online Library, 2009, pp. 25–33 Search PubMed.
- C. Huang, J. Gao, W. Yu and C. Zhou, Macromolecules, 2012, 45, 8420–8429 CrossRef CAS.
- H.-j. Chung, K. Ohno, T. Fukuda and R. J. Composto, Nano Lett., 2005, 5, 1878–1882 CrossRef CAS PubMed.
- C. Özdilek, S. Bose, J. Leys, J. W. Seo, M. Wübbenhorst and P. Moldenaers, Polymer, 2011, 52, 4480–4489 CrossRef PubMed.
- T. Kwon, T. Kim, F. b. Ali, D. J. Kang, M. Yoo, J. Bang, W. Lee and B. J. Kim, Macromolecules, 2011, 44, 9852–9862 CrossRef CAS.
- A. Walther, K. Matussek and A. H. Muller, ACS Nano, 2008, 2, 1167–1178 CrossRef CAS PubMed.
- S. H. Lee, M. Kontopoulou and C. B. Park, Polymer, 2010, 51, 1147–1155 CrossRef CAS PubMed.
- H. Kausch and G. Michler, J. Appl. Polym. Sci., 2007, 105, 2577–2587 CrossRef CAS.
- B. Fernández-d'Arlas, U. Khan, L. Rueda, J. N. Coleman, I. Mondragon, M. A. Corcuera and A. Eceiza, Compos. Sci. Technol., 2011, 71, 1030–1038 CrossRef PubMed.
- L. T. James Korley, S. M. Liff, N. Kumar, G. H. McKinley and P. T. Hammond, Macromolecules, 2006, 39, 7030–7036 CrossRef.
- S. B. Kharchenko, J. F. Douglas, J. Obrzut, E. A. Grulke and K. B. Migler, Nat. Mater., 2004, 3, 564–568 CrossRef CAS PubMed.
- J. Ren and R. Krishnamoorti, Macromolecules, 2003, 36, 4443–4451 CrossRef CAS.
- Y. M. Boiko, W. Brostow, A. Y. Goldman and A. Ramamurthy, Polymer, 1995, 36, 1383–1392 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |