DOI:
10.1039/C4RA09358E
(Paper)
RSC Adv., 2014,
4, 57903-57915
Mechanical and thermodynamical properties of hexagonal compounds at optimized lattice parameters from two-dimensional search of the equation of state
Received
27th August 2014
, Accepted 20th October 2014
First published on 20th October 2014
Abstract
We have calculated the mechanical and thermodynamical properties of selected hexagonal structures by using the optimized lattice parameters (a and c) from two-dimensional (2D) search of the equation of state (EOS) within the appropriate exchange–correlation functional. To overcome the deficiency of density functional theory (DFT) for compounds with localized electrons, a PBE + U approximation was used with our calculated effective U parameter. For calculating the elastic constants of hexagonal structure, the Hex-elastic package was used which is compatible with the highly accurate all electron full-potential (Linearized) augmented plane-wave plus local orbital [FP-(L)APW + lo] method as implemented in the WIEN2k code. The obtained results of the 2D-search of the EOS for the optimized lattice parameters (a and c) are in good agreement with the experimental data. This method clearly shows its superiority compared to the 1D-search of the EOS method. Furthermore, the obtained elastic constants by using the optimized lattice parameters (a and c) from the 2D-search, were in good agreement with the available experimental data and better than the previous theoretical calculations. Our calculations show that the PBE + U approximation improves the results for elastic constants. Consequently, we can claim the following predictions; first, we suggest the value of Poisson's ratio as a boundary condition to predict the type of bonds. Second, we make a one-to-one correspondence between two quantities, shear modulus and C55. Third, we predict the stiffness of the material from the Debye temperature and average sound velocity.
Introduction
Nowadays with increasing computational power, there is much effort and growing interest in the field of elastic constants and improving the search method to find the equation of state, especially for hexagonal compounds with two degrees of freedom, i.e. volume and  changes. Elastic constants link the stress to strain and distinguish the elastic and plastic regimes due to the elastic stability criteria. In turn, these parameters can describe the response of crystals to external forces on solid materials by using first principle calculations1–8 due to their technological important properties such as stiffness, hardness, and brittle/ductility. Moreover, other mechanical properties such as Voigt, Reuss, and Hill bulk moduli, shear and Young's moduli as well as Poisson's ratio3,9 are estimated from elastic coefficients. They also make a connection with thermodynamical properties such as transverse and longitudinal sound velocities, specific heat, Debye temperature, and melting point.9 In addition, based on the calculated elastic constants, we are able to define the elastic anisotropy ratio, which is an important physical quantity for the structural phase stability of crystal structures.9 Based on these evidences one can conclude that the calculation of elastic constants for solid materials, is very attractive and important. Therefore, elastic constants can be the physical quantities for evaluating of accuracy and validity for the employed methods, thus the elastic constants can be a level of accuracy for the employed method, especially based on density functional theory (DFT), one of the most accurate schemes for the band structure calculations.
changes. Elastic constants link the stress to strain and distinguish the elastic and plastic regimes due to the elastic stability criteria. In turn, these parameters can describe the response of crystals to external forces on solid materials by using first principle calculations1–8 due to their technological important properties such as stiffness, hardness, and brittle/ductility. Moreover, other mechanical properties such as Voigt, Reuss, and Hill bulk moduli, shear and Young's moduli as well as Poisson's ratio3,9 are estimated from elastic coefficients. They also make a connection with thermodynamical properties such as transverse and longitudinal sound velocities, specific heat, Debye temperature, and melting point.9 In addition, based on the calculated elastic constants, we are able to define the elastic anisotropy ratio, which is an important physical quantity for the structural phase stability of crystal structures.9 Based on these evidences one can conclude that the calculation of elastic constants for solid materials, is very attractive and important. Therefore, elastic constants can be the physical quantities for evaluating of accuracy and validity for the employed methods, thus the elastic constants can be a level of accuracy for the employed method, especially based on density functional theory (DFT), one of the most accurate schemes for the band structure calculations.
Besides, to find the elastic constants at zero-pressure based on the energy approach,10 we have to calculate the optimized volume from EOS, because of 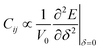 . Usually for hexagonal compounds with two degrees of freedom, EOS is calculated with constant
. Usually for hexagonal compounds with two degrees of freedom, EOS is calculated with constant 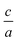 ratio (1D-search of EOS) while in our research to find the elastic constants of hexagonal compounds, we are interested to improve the method of search for evaluation EOS and calculate the optimized volume with 2D-search of EOS.11 In this regards, we use 2D optimize package12 and apply the appropriate exchange–correlation functional. To overcome the deficiency of DFT for the compounds with localized electrons, we apply PBE + U approximation using our calculated U parameter.
ratio (1D-search of EOS) while in our research to find the elastic constants of hexagonal compounds, we are interested to improve the method of search for evaluation EOS and calculate the optimized volume with 2D-search of EOS.11 In this regards, we use 2D optimize package12 and apply the appropriate exchange–correlation functional. To overcome the deficiency of DFT for the compounds with localized electrons, we apply PBE + U approximation using our calculated U parameter.
Theoretical background
In following, a brief summary of theoretical background for the field of elastic constants calculations, 2D-search of EOS and the calculation of effective Hubbard U parameter have been reviewed.
Elastic constants
Elastic constants are defined by Taylor expansion of the total energy E(V, δ) of the lattice distortion (R′) with respect to a small strain (δ) of the lattice, where R′ is expressed by R, the matrix of Bravais lattice vectors of hexagonal symmetry, multiplied by a symmetric distortion matrix, i.e. (R′ = R × D). In Voigt notation, the symmetric distortion matrix is written as:| |
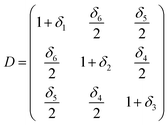 | (1) |
We express the energy of strained system by a Taylor expansion in the distortion parameters.
| |
 | (2) |
τi are related to the strain on the crystal,
Cij are elastic constants and
V0 is the volume of unstrained hexagonal system.
Since hexagonal compounds, have five independent elastic constants, called C11, C12, C13, C33, and C55 (ref. 13) (C55 = C44), therefore, we need five different strains to determine these elastic constants. The five distortions that are used in the Hex-elastic package14 along with energy equations are described as below:
| |
 | (3) |
| | |
E(V, δ) = E(V0, 0) + V0δ(τ1 + τ2) + V0((C11 + C12)δ2 + O(δ3))
| (4) |
| |
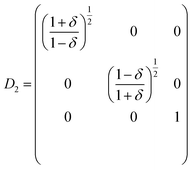 | (5) |
| | |
E(V, δ) = E(V0, 0) + V0((C11 − C12)δ2 + O(δ3))
| (6) |
| |
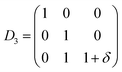 | (7) |
| |
 | (8) |
| |
 | (9) |
| | |
E(V, δ) = E(V0, 0) + V0δ(τ5) + V0(2C55δ2 + O(δ3)), C55 = C44
| (10) |
| |
 | (11) |
| |
 | (12) |
and
| | |
CZZ = C11 + C12 + 2C33 − 4C13
| (13) |
Using the calculated elastic constants, other structural properties such as bulk (B), shear (S) and Young's (E) moduli and dimensionless Poisson's ratio ν (BSEν) are estimated based on Voigt, Reuss, and Hill's approximations.15–17 For hexagonal structure, the above parameters are given by following equations;
| |
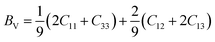 | (14) |
| |
 | (15) |
| |
 | (16) |
| |
 | (17) |
| |
 | (18) |
| |
 | (19) |
| |
 | (20) |
| |
 | (21) |
where
Cij and
Sij denote the elastic constants and elastic compliances, respectively.
Since Voigt and Reuss equations (VRe) represent the upper and lower limits of BSEν properties,17 hence thermodynamical properties such as average sound velocity (vm) which is consist of the longitudinal (vl) and transversal (vt) sound velocities and Debye temperature (θD) are calculated by using Hill scheme17 which is average of VRe, and by using following equations;
| |
 | (22) |
| |
 | (23) |
| |
 | (24) |
where
h is Plank's constant,
kB is the Boltzmann's constant,
Va is the atomic volume and
ρ is mass density of material.
Two dimensional search
In this research, we performed a convenient volume and 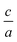 structure optimization by using 2Doptimize package12 for hexagonal compounds. That means to find the optimized lattice parameters (a and c) we have performed at least 25 self-consistent calculations.
structure optimization by using 2Doptimize package12 for hexagonal compounds. That means to find the optimized lattice parameters (a and c) we have performed at least 25 self-consistent calculations.
In this package, firstly for each volume we find the optimized 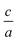 ratio, then we select a set of
ratio, then we select a set of 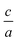 changes and then by using the following equation:
changes and then by using the following equation:
| | |
E(X) = a0 + a1X + … + anXn (n = 2, 3, 4)
| (25) |
(n and x represent the order of fitting and 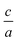 ratio, respectively) we find the best
ratio, respectively) we find the best 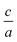 ratio for each volume in the way that the energy has minimum value.
ratio for each volume in the way that the energy has minimum value.
In the next step, we would have a set of energy values and volumes at optimized 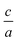 ratio and then by using the included supported equation of states, i.e. EOS2, Murnaghan and Brich–Murnaghan, the minimum total energy and the equilibrium volume are calculated.
ratio and then by using the included supported equation of states, i.e. EOS2, Murnaghan and Brich–Murnaghan, the minimum total energy and the equilibrium volume are calculated.
After that, to find 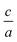 ratio at the equilibrium volume, 2Doptimize package fits the optimized
ratio at the equilibrium volume, 2Doptimize package fits the optimized 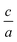 ratios for each volume on the polynomial.
ratios for each volume on the polynomial.
| | |
coa(v) = b0 + b1v + … + bnvn (n = 2, 3, 4)
| (26) |
Where coa and
v denote the

ratio and volume, respectively.
Finally, 2Doptimize package calculates optimized 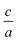 ratio at the optimized volume, by using the above equation.
ratio at the optimized volume, by using the above equation.
Effective Hubbard U parameter
In order to calculate the effective Hubbard U parameter, we have used the method of Anisimov and Gunnarsson,18 which is based on the Linearized Muffin-Tin Orbital (LMTO) basis set. Since this method cannot be used within the LAPW method, Madsen and Novák19 moved the localized electrons from valence to core states to avoid of hybridization.
In practice, in this method we make a 2 × 2 × 2 supercell with one impurity site. Then, by using the following equation
| |
 | (27) |
we performed two calculations, and after that, we moved the localized electrons from valence to core states and eliminated them from valence states by increasing linearization energy at a very high value. In the above equation
n is number of localized electrons at impurity site,
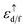
and
εF are the spin up eigenvalue of localized electron (d or f electrons) and Fermi energy, respectively, the spin up eigenvalue, are weighted as a function of spin up relativistic quantum number. The calculated effective Hubbard
U parameter for MnAs, Gd, Gd
2In and Tb compounds were listed in
Table 1.
Table 1 The calculated effective Hubbard U parameter for Gd, Tb, Gd2In and MnAs
| Compound |
Ueff |
| Gd |
0.500 |
| Tb |
0.250 |
| MnAs |
0.073 |
| Gd2In |
GdI |
GdII |
| 0.500 |
0.510 |
Details of calculations
The first-principles calculations of mechanical and thermodynamical properties presented in this paper, were performed using Hex-elastic package14 based on the second-order derivative (E′′(δ)) of the polynomial fit of energy (E = E(δ)) vs. strains, at zero strain (δ = 0), which is completely compatible with WIEN2k package.20 The WIEN2k is an ab initio full potential linearized augmented plane wave (FP-LAPW) plus local orbital method for calculating the electronic ground state of the periodic systems based on DFT.
In this procedure, the unit cell volume is divided into the non-overlapping atomic spheres around each atom with Muffin-Tin radius (Rmt) and the remaining is interstitial area. Two different types of basis functions are used in these regions. In the atomic spheres, the wave functions are expanded into atomic orbitals and the maximum angular momentum of this basis function is set to lmax = 9/10, while in the interstitial region, a plane-wave basis set is used and the convergence of this basis set is checked by a cutoff parameter RmtKmax = 8/9 where Rmt is the smallest atomic sphere radius in the unit cell. Updating the positions, were done until forces drop below 1 mRy per bohr during elastic constants calculations. To treat the exchange–correlation functional, we used the improved generalized gradient approximation (PBE)21 which is the recommended option11,22 except for Re, Ru, and Os compounds,11 in which we applied WC23 instead of the PBE functional. Moreover, we used PBE + U approximation for MnAs, Gd, Gd2In and Tb compounds to overcome the deficiency of DFT for the compounds with localized electrons.
Result and discussion
Two-dimensional calculation
In the first step of these calculations, we have performed 1D and 2D-search of EOS for Tm within PBE functional (see Fig. 1). It shows that the effect of 2D-search, i.e. a convenient volume and 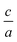 structure optimization, is important. As one can see from Fig. 1, 2D-search of EOS, predicts the smaller optimized volume and lower energy rather than 1D-search of EOS for Tm metal, which is consistent with experimental volume.11
structure optimization, is important. As one can see from Fig. 1, 2D-search of EOS, predicts the smaller optimized volume and lower energy rather than 1D-search of EOS for Tm metal, which is consistent with experimental volume.11
 |
| | Fig. 1 1D and 2D-search of EOS for hexagonal Tm-metal within PBE exchange–correlation approximation. | |
In Fig. 2, we have compared the optimized volume, energy and bulk modulus for some hexagonal compounds with 2D and 1D-search of EOS.
 |
| | Fig. 2 difference between the optimized energy (in Ry), volume (bohr3) and bulk modulus (in GPa) with 1D and 2D-search of EOS for some hexagonal compounds. | |
Fig. 2 shows that the 2D-search of EOS, predicts the optimized energy lower than 1D-search. However, this difference may be negligible but as can be seen from Fig. 2, these differences can influence the optimized volume and bulk modulus. Consequently, the accuracy of DFT which is achieved by using 2D-search of EOS is much better than that obtained by 1D-search.
Therefore, in order to increase the accuracy of the elastic constants calculations, we have calculated the cell parameters of the investigated compounds using 2D-search of EOS, which are listed in Table 2 along with previous theoretical results and the experimental data to seek meaning comparison.11,24–35
Table 2 The calculated a-lattice and c-lattice constants in unit of Angstrom within PBE exchange–correlation potentials except for Re, Ru and Os compounds which we applied WC instead of the PBE functional, in comparison with experimental data and the previous theoretical results obtained from different methods of calculations, bold fonts are our calculations
| Solid |
Symmetry |
a |
c |
Other |
Exp. |
| a |
c |
a |
c |
| Ref. 24 TB calculation. Ref. 25 and 26. Ref. 11. Ref. 27 GGA calculation. Ref. 28. Ref. 29 PBE calculation. Ref. 30. Ref. 31. Ref. 32. Ref. 33. Ref. 34. Ref. 35. |
| Sc |
194 (P63/mmc) |
3.3048 |
5.2057 |
3.2600a |
4.9100a |
3.3100b |
5.2761b |
| Y |
194 (P63/mmc) |
3.6580 |
5.6728 |
3.5900a |
5.3500a |
3.6500b |
5.7342b |
| Ti |
194 (P63/mmc) |
2.9346 |
4.6617 |
2.9700a |
4.8000a |
2.9500b |
4.6800b |
| Zr |
194 (P63/mmc) |
3.2331 |
5.1710 |
2.9900a |
5.5700a |
3.2300b |
5.1500b |
| Tc |
194 (P63/mmc) |
2.7517 |
4.4104 |
2.7200a |
4.3400a |
2.7400b |
4.3950c |
| Re |
194 (P63/mmc) |
2.7585 |
4.4599 |
2.7800a |
4.3900a |
2.7600b |
4.4576b |
| Ru |
194 (P63/mmc) |
2.7015 |
4.2736 |
2.6800a |
4.2600a |
2.7100b |
4.2768c |
| Os |
194 (P63/mmc) |
2.7357 |
4.3248 |
2.7500a |
4.3100a |
2.7400b |
4.3200b |
| Gd |
194 (P63/mmc) |
3.6402 |
5.8258 |
|
|
3.6400c |
5.7803c |
| Tb |
194 (P63/mmc) |
3.5851 |
5.7809 |
|
|
3.6000c |
5.6919c |
| MnAs |
194 (P63/mmc) |
3.6822 |
5.4987 |
3.8400d |
5.6832d |
3.7238e |
5.7045e |
| TiB2 |
191 (P6/mmm) |
3.0340 |
3.2346 |
3.0292f |
3.2198f |
3.0320g |
3.2290g |
| AgB2 |
191 (P6/mmm) |
3.0212 |
4.0659 |
2.9860, 2.9940, 3.0000, 3.0340h |
4.0430, 4.0510, 3.4930, 4.0850h |
3.0000i, 3.0700j |
3.2400i, 3.1800j |
| Gd2In |
194 (P63/mmc) |
5.4546 |
6.7981 |
|
|
5.1390k, 5.4130l |
6.6600k, 6.7500l |
Elastic constants calculation
The complete sets of zero-pressure and zero-temperature single crystal's elastic constants of hexagonal compounds are calculated by using Hex-elastic package14 at their optimized lattice constants from 2D-search of EOS. These are listed in Table 2, in comparison with available experiments and previous theoretical calculations.
By using first-principle calculations and elastic constants, it is possible to estimate the technological important properties such as stiffness, hardness, brittle/ductility and type of bonds for crystal structures.
A material behaves as a brittle (ductility) if the 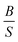 ratio is less (more) than 1.75.8 The sign of Cauchy pressure (C12 − C55) can be used to predict the type of bonds. Usually, the Cauchy pressure of compounds with more dominant covalent (ionic) bonds is negative (positive).7 On the other hand, the value of Poisson's ratio can be used to predict the type of bonds. Stiffness is resistance to deformation forces. Young's modulus, as the ratio of stress and strain, is representative of the stiffness. It means that the greater the value of Young's modulus (E), the stiffer the material is. Hardness is related to how much the material is resistant to the shape changes. There are two representatives for it; (i) bulk modulus, which is related to the resistance against the volume changes and (ii) shear modulus, which is related to the resistance against the reversible deformations. Therefore, it is clear that shear modulus can be a better predictor for hardness.8
ratio is less (more) than 1.75.8 The sign of Cauchy pressure (C12 − C55) can be used to predict the type of bonds. Usually, the Cauchy pressure of compounds with more dominant covalent (ionic) bonds is negative (positive).7 On the other hand, the value of Poisson's ratio can be used to predict the type of bonds. Stiffness is resistance to deformation forces. Young's modulus, as the ratio of stress and strain, is representative of the stiffness. It means that the greater the value of Young's modulus (E), the stiffer the material is. Hardness is related to how much the material is resistant to the shape changes. There are two representatives for it; (i) bulk modulus, which is related to the resistance against the volume changes and (ii) shear modulus, which is related to the resistance against the reversible deformations. Therefore, it is clear that shear modulus can be a better predictor for hardness.8
In this paper for each compound, we defined a word like “MJNK” where M stands for I (ionic) or C (covalent) bonds based on the Cauchy pressure prediction, J for B (brittle) or D (ductility) and N (K) stands for Hn (Sm) where H (S) means hardness (stiffness) and index n (m) shows the ordering of compound in terms of hardness, based on the shear modulus calculation, (stiffness-using Young's modulus) in this research. Moreover at the end of this section, we will check the ordering of compound in terms of hardness by using new offered Vickers hardness and correlation between ductile/brittle and ionic/covalent concepts.
Our calculated elastic constants for Sc are summarized in Table 3, in comparison with available experimental data.36–42 To the best of our knowledge no theoretical value for the elastic constants of scandium available in literature, hence our results can serve as a reference for future investigations. We should emphasize that our calculated results agree well with experimental data.36–42 Our calculations 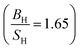 result show that the Sc is a brittle material, however this value is near to 1.75, while experiments predict that it behaves as a ductile
result show that the Sc is a brittle material, however this value is near to 1.75, while experiments predict that it behaves as a ductile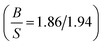 . This inconsistency can be considered from the fact that our calculations are at zero temperature, while the experiments are at 303 K. Therefore, our PBE calculations result shows that the Sc behaves as an IBH4S4 material at zero-temperature. Future experimental work will testify our calculated results.
. This inconsistency can be considered from the fact that our calculations are at zero temperature, while the experiments are at 303 K. Therefore, our PBE calculations result shows that the Sc behaves as an IBH4S4 material at zero-temperature. Future experimental work will testify our calculated results.
Table 3 The calculated elastic constant (Cij in GPa), Bulk modulus (B), Shear modulus (S) and Young's modulus (E) in Voigt (V)–Reuss (R)–Hill (H) approximations (in GPa), Poisson's ratio (ν), transverse elastic wave velocity (νt in m s−1), longitudinal elastic wave velocity (vl in m s−1), average wave velocity (vm in m s−1) and Debye temperature (θD in K) for Sc, Y, and Ti compounds in comparison with available experimental and theoretical data, this work (bold)
| |
Sc |
Y |
Ti |
| PBE |
Exp. (T = 27 °C) (T = 303 K) |
PBE |
Other |
Exp. (T = 27 °C) |
PBE |
Other |
Exp. |
| Ref. 36. Ref. 37. Ref. 38. Ref. 41. Ref. 42. Ref. 39. Ref. 40. Ref. 43 LMTO: full potential linear muffin-tin orbital method. Ref. 44 PBE calculations. Ref. 45. |
| C11 |
92.87 |
99.30a,b, 98.10c, 98.60d |
77.43 |
80.60i |
77.90a,c |
174.08 |
175.00j |
160.00a,b, 162.40k |
| C12 |
31.73 |
39.70a,b, 45.70c, 44.80d |
23.85 |
18.40i |
29.20a,c |
88.25 |
82.60j |
90.00a,b, 92.00k |
| C13 |
30.06 |
29.40a,b, 29.40c, 29.50d |
21.29 |
27.10i |
21.00c, 20.00a |
76.01 |
74.70j |
66.00a,b, 69.00k |
| C33 |
90.60 |
107.00a,b, 105.10c, 106.20d |
80.94 |
88.10i |
76.90a,c |
189.24 |
196.00j |
181.00a,b, 180.70k |
| C55 |
31.41 |
27.70a,b, 27.20c, 27.50d |
22.39 |
31.10i |
24.70c, 24.30a |
43.27 |
41.80j |
46.50a,b, 46.70k |
| BV |
51.11 |
|
40.96 |
|
|
113.10 |
|
|
| BR |
51.09 |
56.60c, 56.70d, 55.87e |
40.96 |
43.80i |
41.20c, 41.18e |
113.10 |
112.10j |
105.00a,b, 105.13e |
| BH |
51.10 |
|
40.96 |
|
|
113.10 |
|
|
| SV |
30.98 |
|
25.60 |
|
|
45.70 |
|
|
| SR |
30.97 |
30.60e, 29.10c |
25.29 |
|
25.60c, 25.40e |
45.19 |
41.00j |
43.40a,b,e |
| SH |
30.97 |
|
25.45 |
|
|
45.45 |
|
|
| EV |
77.31 |
|
63.57 |
|
|
120.83 |
|
|
| ER |
77.30 |
77.60e, 74.40c |
62.92 |
|
63.50c, 63.20e |
119.64 |
109.70j |
162.90a,b, 114.40e |
| EH |
77.30 |
|
63.24 |
|
|
120.23 |
|
|
| vV |
0.247 |
|
0.241 |
|
|
0.321 |
|
|
| vR |
0.247 |
0.268e, 0.279c |
0.243 |
|
0.243c, 0.244e |
0.323 |
0.337j |
0.318a,b, 0.319e |
| vH |
0.247 |
|
0.242 |
|
|
0.323 |
|
|
| θD |
363.04 |
346.00f, 360.00g, 355.00d |
245.39 |
|
248.00f |
405.91 |
|
420.00f |
| Vt |
3196.06 |
|
2380.22 |
|
|
3152.69 |
|
|
| Vl |
5520.22 |
|
4083.26 |
|
|
6163.52 |
|
|
| Vm |
3547.36 |
|
2640.24 |
|
|
3531.84 |
|
|
In Table 3, we have compared our results of Y compound with the computational data of Fast et al.43 obtained by using full potential linear Muffin-Tin orbital (LMTO) method and experimental data.36,38,39,42 One can see that our results agree well with the experimental data and much better than Fast et al.43 calculations. Our Cauchy pressure (C12 − C55 > 0) within PBE predicts that for Y, ionic bonds are more dominant which is consistent with the prediction of Cauchy pressure using experimental elastic constants. While previous theoretical calculations predict that, the sign of Cauchy pressure is negative, it means that for Y, covalent bonds are more dominant. Therefore, our results within PBE, define Y as an IBH2S2 material. Our calculated elastic constants within PBE for Ti compound are given in Table 3 along with previous theoretical calculations and experimental data. It is clear that our results are in very good agreement with the experimental data36,37,39,42,45 in comparison to the previous calculations.44 Therefore, our calculations within PBE exchange–correlation, predict that, Ti behaves as an IDH7S8 material. Table 4, presents the simulated calculations of the elastic constants for Zr compound along with the experimental data and the previous theoretical calculations. Our results agree well with the both previous experimental and theoretical calculations.38,46–53 In additional we have calculated Debye temperature of Zr, which show very good agreement with experimental data. Our results predict that Zr as a ductile material within PBE, and predict ionic nature for the bonds (IDH6S6), while the Poisson's ratio 0.332 (see ref. 31) predicts that Zr exhibit metallic bonding which is consistent with the experimental data (0.35). The calculated results of Tc within PBE were listed in Table 4 in comparison with available experimental and theoretical data.38,43,54 Our calculated bulk modulus is better than the previous calculations and show good agreement with experimental data. To our knowledge, there are no experimental and theoretical data for Debye temperature of Tc. We hope that, our results provide a useful reference for future experimental works and theoretical studies. Our calculation predicts that dominant bonds for Tc, are ionic which agree with the previous prediction using elastic constants.43 Our calculations exhibit that Tc behaves as a ductile material, which is consistent with the experimental data.54 Therefore, based on our PBE calculations, Tc is an IDH10S10 material.
Table 4 The calculated elastic constant (Cij in GPa), Bulk modulus (B), Shear modulus (S) and Young's modulus (E) in Voigt (V)–Reuss (R)–Hill (H) approximations (in GPa), Poisson's ratio (v), Transverse elastic wave velocity (νt in m s−1), longitudinal elastic wave velocity (νl in m s−1), average wave velocity (νm in m s−1) and Debye temperature (θD in K) for Zr and Tc compounds in comparison with available experimental and theoretical data, this work (bold)
| |
Zr |
|
|
Tc |
| PBE |
Other |
Exp. |
PBE |
Other |
Exp. |
| Ref. 46. Ref. 47 FP-LMTO calculation. Ref. 48 DFT calculation. Ref. 49 TB calculation. Ref. 50 EAM calculation. Ref. 51 MEAM calculation. Ref. 52 MEAM calculation. Ref. 53. Ref. 38. Ref. 39. Ref. 43 LMTO calculation. Ref. 54. |
| C11 |
145.28 |
141.10a, 153.10b, 139.40c, 142.00d, 147.90e, 151.50f, 152.00g |
144.00h |
525.41 |
611.70k |
|
| C12 |
63.86 |
67.60a, 63.40b, 71.30c, 71.00d, 66.30e, 71.80f, 74.00g |
74.00h |
229.73 |
218.70k |
|
| C13 |
66.46 |
64.30a, 76.50b, 66.30c, 71.00d, 66.20e, 66.10f, 63.20g |
67.00h |
184.72 |
207.50k |
|
| C33 |
165.39 |
166.90a, 171.20b, 162.70c, 147.00d, 182.70e, 160.60f, 153.30g |
166.00h |
596.32 |
645.00k |
|
| C55 |
27.51 |
25.80a, 22.40b, 25.50c, 8.00d, 39.20e, 34.10f, 33.20g |
33.00h |
160.02 |
196.60k |
|
| BV |
94.39 |
|
|
316.16 |
|
|
| BR |
93.97 |
|
|
316.04 |
348.60k |
281.00l |
| BH |
94.18 |
|
|
316.10 |
|
|
| SV |
36.42 |
|
|
163.44 |
|
|
| SR |
34.76 |
|
|
161.33 |
|
123.00l |
| SH |
35.59 |
|
|
162.39 |
|
|
| EV |
96.81 |
|
|
418.25 |
|
|
| ER |
92.84 |
|
|
413.62 |
|
|
| EH |
94.83 |
|
|
415.93 |
|
|
| vV |
0.329 |
|
|
0.279 |
|
|
| vR |
0.335 |
|
0.35i |
0.281 |
|
0.310l |
| vH |
0.332 |
|
|
0.280 |
|
|
| θD |
273.77 |
|
290.00j |
517.27 |
|
|
| Vt |
2345.11 |
|
|
3798.88 |
|
|
| Vl |
4678.12 |
|
|
6880.01 |
|
6220.00i (in T = 25 °C) |
| Vm |
2630.37 |
|
|
4233.05 |
|
|
Single elastic constants for Re within WC23 exchange–correlation are listed in Table 5. Currently, there is no theoretical calculation of single elastic constants are available in the literature. Our calculated elastic constants, agree well with the experimental data25,36,39,42,43,45 especially our calculated Debye temperature.39 Table 5 exhibit that Re is a ductile and stiff material and also predicts that the dominant bonds are ionic (IDH11S11).
Table 5 The calculated elastic constant (Cij in GPa), Bulk modulus (B), Shear modulus (S) and Young's modulus (E) in Voigt (V)–Reuss (R)–Hill (H) approximations (in GPa), Poisson's ratio (v), transverse elastic wave velocity (νt in m s−1), longitudinal elastic wave velocity (νl in m s−1), average wave velocity (νm in m s−1) and Debye temperature (θD in K) for Re, Ru, and Os compounds in comparison with available experimental and theoretical data, this work (bold)
| |
Re |
Ru |
Os |
| WC |
Other |
Exp. |
WC |
Other |
Exp. |
WC |
Other |
Exp. |
| Ref. 45. Ref. 36. Ref. 43 LMTO calculation. Ref. 25. Ref. 42. Ref. 39. |
| C11 |
649.00 |
|
634.40a, 616.00b |
622.52 |
701.00d |
563.00e |
816.26 |
894.50c |
|
| C12 |
269.39 |
|
266.00a, 273.00b |
202.99 |
169.20d |
188.00e |
225.23 |
249.20c |
|
| C13 |
187.64 |
|
202.00a, 206.00b |
179.81 |
187.40d |
168.00e |
256.13 |
245.60c |
|
| C33 |
678.16 |
|
701.10a, 683.00b |
724.57 |
774.50d |
624.00e |
914.98 |
1016.40c |
|
| C55 |
184.95 |
|
169.10a, 161.00b |
212.42 |
240.00d |
181.00e |
312.70 |
162.20c |
|
| BV |
362.83 |
|
|
343.87 |
|
|
446.94 |
|
|
| BR |
362.43 |
447.30c |
372.00d, 365.25e |
342.98 |
368.80d |
310.92e, 320.80d |
444.92 |
476.10c, 411.89e |
418.00d |
| BH |
362.63 |
|
|
343.42 |
|
|
445.93 |
|
|
| SV |
200.71 |
|
|
220.72 |
|
|
304.85 |
|
|
| SR |
197.69 |
|
178.80e |
219.13 |
|
191.10e |
304.38 |
275.20e |
|
| SH |
199.20 |
|
|
219.93 |
|
|
304.61 |
|
|
| EV |
508.38 |
|
|
545.46 |
|
|
745.14 |
|
|
| ER |
501.83 |
|
461.10e |
541.98 |
|
475.80e |
743.56 |
675.20e |
|
| EH |
505.11 |
|
|
543.72 |
|
|
744.35 |
|
|
| vV |
0.266 |
|
|
0.235 |
|
|
0.222 |
|
|
| vR |
0.269 |
|
0.290e |
0.236 |
|
0.245e |
0.221 |
0.227e |
|
| vH |
0.267 |
|
|
0.236 |
|
|
0.221 |
|
|
| θD |
416.08 |
|
416.00f |
582.94 |
|
555.00f |
502.37 |
|
467.00f |
| Vt |
3076.93 |
|
|
4206.67 |
|
|
3676.42 |
|
|
| Vl |
5464.27 |
|
|
7157.37 |
|
|
6148.81 |
|
|
| Vm |
3423.22 |
|
|
4662.72 |
|
|
4068.39 |
|
|
The simulated elastic constants of Ru using FPLAPW-WC are listed in Table 5 in comparison with theoretical LMTO calculations43 and experimental measurements.25,39,42 It is clear that our results are in good agreement with the experimental data and better than pervious calculations. Our 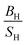 ratio (1.56) and experimental value (1.63), suggest that Ru behaves as a brittle material. The present value of Young's and shear moduli are high, therefore it is suggested that Ru is stiffer and hardness. These results within WC exchange–correlation, suggest that Ru should be considered as a CBH12S12 material, while the Poisson's ratio 0.236 (see ref. 31 and reference therein) predicts that Ru exhibit ionic bonding which is consistent with the experimental elastic constants prediction. The elastic constants of Os along with previous theoretical calculations are listed in Table 5. Our results within WC exchange–correlation are in reasonable agreement with previous calculations.42,43 However, our calculated C55 is 312.7 GPa, while the previous calculated value was 162.2 GPa.43 This difference leads to the different signs of Cauchy pressure (C12 − C55) for our results than the previous calculations.43 Therefore, our (previous43) results predict that covalent (ionic) bonds are more dominant for Os compound, while the Poisson's ratio 0.221 (see ref. 31 and reference therein) predicts that Os exhibit ionic bonding.
ratio (1.56) and experimental value (1.63), suggest that Ru behaves as a brittle material. The present value of Young's and shear moduli are high, therefore it is suggested that Ru is stiffer and hardness. These results within WC exchange–correlation, suggest that Ru should be considered as a CBH12S12 material, while the Poisson's ratio 0.236 (see ref. 31 and reference therein) predicts that Ru exhibit ionic bonding which is consistent with the experimental elastic constants prediction. The elastic constants of Os along with previous theoretical calculations are listed in Table 5. Our results within WC exchange–correlation are in reasonable agreement with previous calculations.42,43 However, our calculated C55 is 312.7 GPa, while the previous calculated value was 162.2 GPa.43 This difference leads to the different signs of Cauchy pressure (C12 − C55) for our results than the previous calculations.43 Therefore, our (previous43) results predict that covalent (ionic) bonds are more dominant for Os compound, while the Poisson's ratio 0.221 (see ref. 31 and reference therein) predicts that Os exhibit ionic bonding.
Our results predict that C13 > C12 while the previous one indicated C12 > C13. The calculated Bulk, Shear and Young's moduli, suggest that Os should be a brittle, stiff and hard material (CBH14S14).
Based on the data gathered in Table 6, it is clear that the effect of Hubbard U parameter correction, improves the result of gadolinium towards the experimental ones.36–39 Prediction of Cauchy pressure (C12 − C55) and Poisson's ratio within PBE and PBE + U approximation about the type of bonds, are similar (for Gd, ionic bonds are more dominant) C12 < C55 PBE and PBE + U approximations predict that Gd is a brittle material but PBE + U approximation 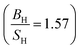 predicts that it is more brittle than PBE approximation
predicts that it is more brittle than PBE approximation 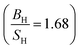 . The higher value of shear modulus within PBE + U approximation indicates that Gd is harder than that obtained within PBE approximation. The higher value of Young's modulus with Hubbard U correction indicates that Gd is stiffer than that obtained within PBE prediction. Therefore, comparing the results of PBE + U approximation for Gd with results of other compounds within different exchange–correlation, indicate Gd as an IBH1S1 material. According to Table 6 (Tb compound) we can observe that PBE + U approximation improves the obtained elastic constants towards the experimental data.39,42,55 Concerning the changes of other parameters, we obtain that the effect of Hubbard U parameter is so important for Tb (see Table 6). The effective Hubbard U parameter changes the order of C12 > C55 (PBE) to C12 < C55 (PBE + U). This means that PBE exchange–correlation predicts that ionic bonds are more dominant for Tb, while Hubbard U correction (PBE + U approximation) changes it from ionic to covalent bonds.
. The higher value of shear modulus within PBE + U approximation indicates that Gd is harder than that obtained within PBE approximation. The higher value of Young's modulus with Hubbard U correction indicates that Gd is stiffer than that obtained within PBE prediction. Therefore, comparing the results of PBE + U approximation for Gd with results of other compounds within different exchange–correlation, indicate Gd as an IBH1S1 material. According to Table 6 (Tb compound) we can observe that PBE + U approximation improves the obtained elastic constants towards the experimental data.39,42,55 Concerning the changes of other parameters, we obtain that the effect of Hubbard U parameter is so important for Tb (see Table 6). The effective Hubbard U parameter changes the order of C12 > C55 (PBE) to C12 < C55 (PBE + U). This means that PBE exchange–correlation predicts that ionic bonds are more dominant for Tb, while Hubbard U correction (PBE + U approximation) changes it from ionic to covalent bonds.
Table 6 The calculated elastic constant (Cij in GPa), Bulk modulus (B), Shear modulus (S) and Young's modulus (E) in Voigt (V)–Reuss (R)–Hill (H) approximations (in GPa), Poisson's ratio (v), transverse elastic wave velocity (vt in m s−1), longitudinal elastic wave velocity (νl in m s−1), average wave velocity (νm in m s−1) and Debye temperature (θD in K) for Gd, Tb, and Gd2In compounds in comparison with available experimental data, this work (bold)
| Gd |
Tb |
Gd2In |
| Gd |
PBE |
PBE + U |
Other |
Exp. (T = 27 °C) |
PBE |
PBE + U |
Exp. |
PBE |
PBE + U |
| Ref. 38. Ref. 36. Ref. 37. Ref. 55. Ref. 39. Ref. 42. |
| C11 |
63.82 |
70.00 |
|
67.83a,b,c |
55.46 |
73.79 |
68.55f |
91.59 |
105.36 |
| C12 |
25.65 |
23.13 |
|
25.59a,b,c |
17.07 |
20.27 |
24.65f |
46.34 |
35.36 |
| C13 |
14.03 |
18.23 |
|
20.73a,b,c |
15.00 |
18.12 |
22.40f |
17.03 |
26.29 |
| C33 |
68.58 |
72.08 |
|
71.23a,b,c |
62.03 |
75.18 |
73.30f |
94.76 |
104.11 |
| C55 |
17.59 |
21.55 |
|
20.77a,b,c |
16.77 |
24.14 |
21.60f |
36.70 |
27.99 |
| BV |
33.74 |
36.81 |
|
|
29.68 |
37.31 |
|
48.75 |
54.52 |
| BR |
33.68 |
36.80 |
|
37.90a,b,c |
29.64 |
37.31 |
38.79f |
48.16 |
54.42 |
| BH |
33.71 |
36.80 |
|
|
29.66 |
37.31 |
|
48.45 |
54.48 |
| SV |
20.35 |
23.47 |
|
|
18.94 |
26.09 |
|
32.38 |
33.32 |
| SR |
19.70 |
23.29 |
|
21.80a,b,c |
18.69 |
25.98 |
22.40f |
30.06 |
32.63 |
| SH |
20.03 |
23.38 |
|
|
18.81 |
26.03 |
|
31.22 |
32.98 |
| EV |
50.83 |
58.07 |
|
|
46.84 |
63.48 |
|
79.52 |
83.05 |
| ER |
49.46 |
57.70 |
|
54.80a,b,c |
46.34 |
63.25 |
56.30f |
74.66 |
81.58 |
| EH |
50.15 |
57.90 |
|
|
46.59 |
63.36 |
|
77.10 |
82.32 |
| vV |
0.248 |
0.237 |
|
|
0.236 |
0.216 |
|
0.228 |
0.246 |
| vR |
0.255 |
0.238 |
|
0.259a,b,c |
0.239 |
0.217 |
0.258f |
0.241 |
0.250 |
| vH |
0.252 |
0.237 |
|
|
0.238 |
0.216 |
|
0.234 |
0.248 |
| θD |
164.32 |
177.27 |
175d |
182 (in T = 0 K)e |
157.17 |
184.45 |
170 ± 11d, 176.00e |
209.70 |
216.00 |
| Vt |
1601.13 |
1730.13 |
|
|
1514.49 |
1881.54 |
|
1954.09 |
2012.71 |
| Vl |
2780.86 |
2950.02 |
|
|
2583.42 |
2963.13 |
|
3319.30 |
3477.59 |
| Vm |
1777.99 |
1918.08 |
|
|
16.76.07 |
1970.42 |
|
2165.61 |
2234.01 |
PBE + U approximation predicts that Tb is harder than the PBE prediction. The higher value of Young's modulus within PBE + U approximation predicts that Tb is stiffer than the prediction of PBE. Hubbard U correction predicts that Tb is more brittle than PBE. Therefore, comparison of our results within PBE + U approximation with other compounds within different exchange–correlations for Tb, indicate that Tb behaves as a CBH3S3 material. We have calculated the mechanical and thermodynamical properties of Gd2In intermetallic compound within PBE and PBE + U approximations. According to the results of Gd2In (Table 6) we can conclude that the effect of Hubbard potential on variation of the elastic constants is important. The Hubbard U correction leads the order of C11 and C33 changes from C11 < C33 to C11 > C33, however this small change could be due to numerical errors in calculations. PBE and PBE + U approximations predict that Gd2In is a brittle material but PBE 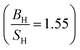 predicts that Gd2In is more brittle than PBE + U prediction
predicts that Gd2In is more brittle than PBE + U prediction 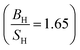 . The higher value of Young's modulus with Hubbard U parameter makes Gd2In stiffer than PBE prediction. PBE and PBE + U approximations predict that ionic bonds are more dominant for Gd2In (C12 > C55), i.e. the prediction of PBE and PBE + U about type of bonds are the same. Thus, in this research Gd2In behaves as an CBH5S5 material.
. The higher value of Young's modulus with Hubbard U parameter makes Gd2In stiffer than PBE prediction. PBE and PBE + U approximations predict that ionic bonds are more dominant for Gd2In (C12 > C55), i.e. the prediction of PBE and PBE + U about type of bonds are the same. Thus, in this research Gd2In behaves as an CBH5S5 material.
Our results for TiB2 are listed in Table 7 along with experimental data,56–59 and previous calculations.31,60 It is clear that our results are in very good agreement with experimental data and much better than previous calculations. Our 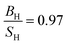 ratio show that TiB2 behaves as a brittle material, which is consistent with experimental prediction and better than previous calculations. The high value of Young's and shear moduli, define TiB2 as a stiff and hard material. Therefore, in this research, TiB2 behaves as a CBH13S13 material within PBE.
ratio show that TiB2 behaves as a brittle material, which is consistent with experimental prediction and better than previous calculations. The high value of Young's and shear moduli, define TiB2 as a stiff and hard material. Therefore, in this research, TiB2 behaves as a CBH13S13 material within PBE.
Table 7 The calculated elastic constant (Cij in GPa), Bulk modulus (B), Shear modulus (S) and Young's modulus (E) in Voigt (V)–Reuss (R)–Hill (H) approximations (in GPa), Poisson's ratio (v), transverse elastic wave velocity (νt in m s−1), longitudinal elastic wave velocity (νl in m s−1), average wave velocity (νm in m s−1) and Debye temperature (θD in K) for TiB2 and AgB2 compounds in comparison with available experimental and theoretical data, this work (bold)
| TiB2 |
AgB2 |
| TiB2 |
PBE |
Other |
Exp. |
PBE |
other |
| Ref. 31 GGA calculation. Ref. 60. Ref. 56. Ref. 57. Ref. 58. Ref. 59. Ref. 66 PBE calculation. |
| C11 |
655.34 |
670.90a, 651.00b |
690.00c, 660.00d, 672.00e, 654.40f |
270.64 |
220.90a, 370.20g |
| C12 |
63.46 |
64.00a, 76.00b |
410.00c, 48.00d, 40.00e, 48.98f |
198.04 |
253.70a, 95.70g |
| C13 |
101.77 |
100.90a, 115.00b |
320.00c, 93.00d, 125.00e, 95.25f |
74.89 |
82.50a, 62.90g |
| C33 |
458.59 |
472.90a, 461.00b |
440.00c, 432.00d, 224.00e, 458.10f |
204.46 |
173.50a, 210.40g |
| C55 |
262.55 |
266.60a, 259.00b |
250.00c, 260.00d, 232.00e, 262.60f |
119.27 |
−42.40a, 7.70g |
| BV |
255.92 |
|
|
160.15 |
|
| BR |
251.38 |
262.00b |
417.00c, 244.00d, 247.50f |
146.37 |
148.40g |
| BH |
253.65 |
|
|
153.26 |
|
| SV |
264.36 |
|
|
81.50 |
|
| SR |
258.45 |
255.00b |
169.00c, 262.00d, 264.30f |
60.08 |
48.40g |
| SH |
261.40 |
|
|
70.79 |
|
| EV |
589.94 |
|
|
209.03 |
|
| ER |
577.44 |
578.00b |
446.00c, 579.00d, 584.70f |
158.55 |
130.90g |
| EH |
583.69 |
|
|
184.03 |
|
| vV |
0.115 |
|
|
0.282 |
|
| vR |
0.117 |
0.130b |
0.323c, 0.104d, 0.106f |
0.319 |
0.353g |
| vH |
0.116 |
|
|
0.299 |
|
| θD |
1216.17 |
1204.50b |
989.00c, 1211.00d, 1217.00f |
490.68 |
408.40g |
| Vt |
7642.57 |
7545.00b |
7660.00f |
3252.82 |
2688.00g |
| Vl |
11599.80 |
11585.90b |
11245.00f |
6084.10 |
5637.00g |
| Vm |
8367.34 |
8272.40b |
8350.00f |
3633.27 |
3023.00g |
The obtained results of AgB2 are listed in Table 7. Kwon et al.61 reported that AgB2 is a potential candidate for high Tc superconductors which confirm by several studies.31–33,62–65 We were interested to study this compound since Shein and Ivanovskii31 reported that it is mechanically unstable (C55 < 0) using elastic constants calculation, whereas Ozisik et al.66 suggested that it is mechanically stable owing to the C55 positive value 7.7 GPa. Our calculated elastic constants, using lattice parameters from 2D-search, are positive which suggests that this compound is mechanically stable which is consistent with Ozisik et al. calculations. The present value of C55 for AgB2 (119.27 GPa) is much higher than the Ozisik et al.66 calculation (7.7 GPa) which indirectly, is a hardness predictor. It means our results show that AgB2 is much hardness. Ozisik et al. calculations predict 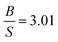 66 for AgB2 compound which is more ductile than our calculation
66 for AgB2 compound which is more ductile than our calculation 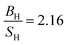 . The comparison of Young's modulus between Ozisik66 and our calculations, demonstrate that AgB2 is stiffer than our calculations. Therefore, our results within PBE suggest that AgB2 is an IDH9S9 material. These differences can be considered from the fact that our calculations are using lattice parameters from 2D-search. Future experimental work will testify our calculated results. The obtained ferromagnetic-results of MnAs, along with experimental data in the paramagnetic state at 303 K (ref. 67) for seeking comparison, are given in Table 8. The effect of Hubbard U parameter, changes the order of elastic constants from C12 < C13 < C55 < C11 < C33 to C13 < C12 < C55 < C33 < C11 when we move from PBE → PBE + U. It is observed that PBE + U approximation, improves the obtained bulk modulus toward experimental values.68 The Hubbard U correction does not change the prediction of Cauchy pressure (C12 − C55) and Poisson's ratio regarding the type of bonds. Both of PBE and PBE + U predict ionic bonds are more dominate for MnAs compound (C12 > C55). Hubbard U correction makes MnAs more brittle than PBE prediction. PBE + U approximation predicts that MnAs is more hard (see the value of shear modulus in Table 8) than PBE prediction. The higher value of Young's modulus within PBE + U approximation, predicts that MnAs is stiffer than the PBE prediction. Therefore, in this work we recognize MnAs as a CBH8S7 material.
. The comparison of Young's modulus between Ozisik66 and our calculations, demonstrate that AgB2 is stiffer than our calculations. Therefore, our results within PBE suggest that AgB2 is an IDH9S9 material. These differences can be considered from the fact that our calculations are using lattice parameters from 2D-search. Future experimental work will testify our calculated results. The obtained ferromagnetic-results of MnAs, along with experimental data in the paramagnetic state at 303 K (ref. 67) for seeking comparison, are given in Table 8. The effect of Hubbard U parameter, changes the order of elastic constants from C12 < C13 < C55 < C11 < C33 to C13 < C12 < C55 < C33 < C11 when we move from PBE → PBE + U. It is observed that PBE + U approximation, improves the obtained bulk modulus toward experimental values.68 The Hubbard U correction does not change the prediction of Cauchy pressure (C12 − C55) and Poisson's ratio regarding the type of bonds. Both of PBE and PBE + U predict ionic bonds are more dominate for MnAs compound (C12 > C55). Hubbard U correction makes MnAs more brittle than PBE prediction. PBE + U approximation predicts that MnAs is more hard (see the value of shear modulus in Table 8) than PBE prediction. The higher value of Young's modulus within PBE + U approximation, predicts that MnAs is stiffer than the PBE prediction. Therefore, in this work we recognize MnAs as a CBH8S7 material.
Table 8 The calculated elastic constant (Cij in GPa), Bulk modulus (B), Shear modulus (S) and Young's modulus (E) in Voigt (V)–Reuss (R)–Hill (H) approximations (in GPa), Poisson's ratio (v), transverse elastic wave velocity (νt in m s−1), longitudinal elastic wave velocity (νl in m s−1), average wave velocity (νm in m s−1) and Debye temperature (θD in K) for ferromagnetic MnAs-compound in comparison with available experimental and theoretical data, this work (bold)
| MnAS |
PBE |
PBE + U |
Other |
Exp. |
| Ref. 67 measured at 303 K and in the paramagnetic state. Ref. 68 measured at 273 K. Ref. 55. |
| C11 |
109.80 |
116.51 |
|
40.00a |
| C12 |
42.72 |
55.37 |
|
8.00a |
| C13 |
43.38 |
15.97 |
|
10.00a |
| C33 |
138.43 |
108.82 |
|
110.00a |
| C55 |
69.47 |
88.55 |
|
34.00a |
| BV |
68.55 |
57.38 |
|
|
| BR |
67.81 |
55.87 |
|
36b |
| BH |
68.18 |
56.63 |
|
|
| SV |
49.73 |
57.30 |
|
|
| SR |
44.59 |
46.41 |
|
|
| SH |
47.16 |
51.86 |
|
|
| EV |
120.15 |
128.97 |
|
|
| ER |
109.72 |
109.04 |
|
|
| EH |
114.98 |
119.19 |
|
|
| vV |
0.207 |
0.125 |
|
|
| vR |
0.230 |
0.174 |
|
|
| vH |
0.218 |
0.149 |
|
|
| θD |
346.29 |
360.48 |
254.40c |
|
| Vt |
2657.19 |
2786.26 |
|
|
| Vl |
4429.63 |
4339.20 |
|
|
| Vm |
2939.57 |
3060.01 |
|
|
Previous studied show that correlation between hardness and shear modulus is not always valid for a large variety of materials as discussed in ref. 69. The new research of Chen et al.69 shows that the calculated Vickers hardness (Hv) as Hv = 2(k2S)0.585 − 3 (k = S/B, S-shear and B-bulk modulus) is a better prediction of hardness than shear modulus. This motivated us to check the hardness of materials in this research by using shear modulus (S) and Vickers hardness (Hv). The ordering of compound in terms of hardness (PBE + U results were used) using our shear modulus calculation (low to high) is as Gd, Y, Tb, Sc, Gd2In, Zr, Ti, MnAs, AgB2, Tc, Re, Ru, Ti2B, and Os. While our Vickers hardness calculation predicts it as Zr, Ti, Gd, Y, Sc, Gd2In, Tb, AgB2, Tc, MnAs, Re, Ru, Os, and Ti2B.
The previous analysis70 on the elastic properties revealed that 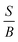 ratio (Pugh's modulus, it can define as
ratio (Pugh's modulus, it can define as 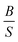 (ref. 8 and 31)) and revised Cauchy pressure
(ref. 8 and 31)) and revised Cauchy pressure 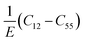 (E-Young modulus) are well correlated to a hyperbolic criterion to recognize the ductile to brittle properties for a large materials of cubic symmetry. This means that there is a correlation between ductility/brittle and metallic/covalent concepts.70 We could find (see Fig. 6) this correlation between ductility/brittle and ionic/covalent concepts for our hexagonal compounds except for Sc, Y, Gd, and Gd2In at zero temperature (PBE + U results were used) which for them our results predict brittle materials and ionic bonds. However, using the mechanism proposed by the previous analysis70 these materials are not exceptions. From Fig. 6, we can see that the Sc, Y, Gd and Gd2In are close to the transformation zone. So, we realize that the mechanism proposed in the previous report70 can be also suitable for the hexagonal compounds.
(E-Young modulus) are well correlated to a hyperbolic criterion to recognize the ductile to brittle properties for a large materials of cubic symmetry. This means that there is a correlation between ductility/brittle and metallic/covalent concepts.70 We could find (see Fig. 6) this correlation between ductility/brittle and ionic/covalent concepts for our hexagonal compounds except for Sc, Y, Gd, and Gd2In at zero temperature (PBE + U results were used) which for them our results predict brittle materials and ionic bonds. However, using the mechanism proposed by the previous analysis70 these materials are not exceptions. From Fig. 6, we can see that the Sc, Y, Gd and Gd2In are close to the transformation zone. So, we realize that the mechanism proposed in the previous report70 can be also suitable for the hexagonal compounds.
 |
| | Fig. 3 Comparison of the sign of Cauchy pressure and the Poisson's ratio for considered hexagonal compounds. The results of PBE + U approximation were used for Gd, Tb, MnAs and Gd2In. | |
 |
| | Fig. 4 Comparison of the behavior of Young's modulus (in GPa), Debye temperature (in K) and average sound velocity (in m s−1) for the considered compounds. The results of PBE + U approximation were used for Gd, Tb, MnAs and Gd2In. | |
 |
| | Fig. 5 Comparison of two quantities C55 and shear modulus (in GPa) for the considered hexagonal compounds. The results of PBE + U approximation were used for Gd, Tb, MnAs and Gd2In. | |
 |
| | Fig. 6 The correlation between ductile/brittle and types of bond. Au is typical metallic and exhibits the most ductile and plastic materials while the Si and diamond are typical covalent bond materials and diamond is known as the hardest material. | |
Base on the previous report70, it is interesting to see that the correlation between ductile/brittle and ionic/covalent concepts derived from the hexagonal compounds can provide us a more clear insight to the relationship between hardness and Pugh's modulus. This means that Pugh's modulus ratio as 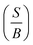 seems to mirror the hardness of materials i.e. hardness increases with increasing Pugh's modulus. For example, the ordering of hardness using shear modulus for Ru and Os will be as Ru, Ti2B, Os while from Fig. 6, using Pugh's modulus, it will be as Ru, Os. In the above, we completed this discussion using Vickers hardness.
seems to mirror the hardness of materials i.e. hardness increases with increasing Pugh's modulus. For example, the ordering of hardness using shear modulus for Ru and Os will be as Ru, Ti2B, Os while from Fig. 6, using Pugh's modulus, it will be as Ru, Os. In the above, we completed this discussion using Vickers hardness.
Moreover our results show that the Poisson's ratio (to predict the type of bonds) follows the 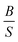 ratio (to predict brittle/ductility of materials) trend. This can again emphasize that there is a correlation between type of bonds and brittle/ductility of materials.
ratio (to predict brittle/ductility of materials) trend. This can again emphasize that there is a correlation between type of bonds and brittle/ductility of materials.
Prediction
The sign of Cauchy pressure (C12 − C55) can be used to predict the type of bonds. Usually, the Cauchy pressure of compounds with more dominant covalent (ionic) bonds is negative (positive).7 On the other hand, the value of Poisson's ratio can be used to predict the type of bonds.8
If we compare the sign of Cauchy pressure and the value of Poisson's ratio, we can offer the typical value of ν = 0.236 as a limit to determine the type of bonds (see Fig. 3). The present value of 0.236, derived from the Cauchy pressure, as a limit to determine the type of bonds is in good agreement with the previous results (see ref. 31 and reference therein).
Stiffness is resistance to deformation forces. Young's modulus, as the ratio of stress and strain, is representative of the stiffness. It means that the greater the value of Young's modulus (E), the stiffer the material is. Fig. 4 shows that, Debye temperature and average sound velocity can be considered as a stiffness predictor, generally. However, we do not see this behavior for Re and Os elements. Hardness is related to how much the material is resistant to the shape changes. There are two representatives; (i) bulk modulus, which is related to the resistance against the volume changes and (ii) shear modulus, which is related to the resistance against the reversible deformations. Therefore, shear modulus can be a better predictor for hardness.8 Fig. 5 shows that shear modulus follows the C55 trend. Therefore, we can usually obtain a larger shear modulus is mainly due to its larger C55.
Conclusions
We performed the 2D-search of EOS to find the optimized lattice parameters (a and c) for hexagonal compounds. By using these parameters, we calculated the zero-pressure and zero-temperature mechanical and thermodynamical properties of the considered compounds. Our results are in very good agreement with experimental data and are better than the previous theoretical calculations. Our results show that the effect of Hubbard U parameter improves the results of elastic constants calculations. Our results based on the shear modulus calculation predict that Gadolinium (Osmium) has the smallest (highest) value of hardness and stiffness in this research. We offered the typical value of ν = 0.236 for Poisson's ratio as a limit to determine the type of bonds. It was observed the Debye temperature or average sound velocity could be used as a stiffness predictor.
Acknowledgements
For the author A. H. Reshak the result was developed within the CENTEM project, reg. no. CZ.1.05/2.1.00/03.0088, co-funded by the ERDF as part of the Ministry of Education, Youth and Sports OP RDI program. Computational resources were provided by MetaCentrum (LM2010005) and CERIT-SC (CZ.1.05/3.2.00/08.0144) infrastructures.
References
- P. Ravindran, L. Fast, P. A. Korzhavyi and B. Johansson, Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2, J. Appl. Phys., 1998, 84, 4891–4904 CrossRef CAS PubMed.
- J. Łazewski, H. Neumann and K. Parlinski, Ab initio elasticity of chalcopyrites, J. Appl. Phys., 2003, 93, 3789 CrossRef PubMed.
- H. Yao, L. Ouyang and W. Y. Ching, ab initio Calculation of elastic Constants of Ceramic Crystals, J. Am. Ceram. Soc., 2007, 90, 3194–3204 CrossRef CAS PubMed.
- D. Connétablel and O. Thomas, First-principles study of the structural, electronic, vibrational, and elastic properties of orthorhombic NiSi, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 094101 CrossRef.
- A. Marmier, P. S. Ntoahae, P. E. Ngoepe, D. G. Pettifor and S. C. Parker, Negative compressibility in platinum sulfide using density-functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 172102 CrossRef.
- H. B. Xu, Y. X. Wang and V. C. Lo, First-principles study of CrB4 as a high shear modulus compounds, Phys. Status Solidi RRL, 2011, 5, 13–15 CrossRef CAS.
- M. G. Brik, First-principles calculations of electronic, optical and elastic properties of ZnAl2S4 and ZnGa2O4, J. Phys. Chem. Solids, 2010, 71, 1435–1442 CrossRef CAS PubMed.
- A. Yildirim, H. Koc and E. Deligoz, First-principles study of the structural, elastic, electronic, optical, and vibrational properties of intermetallic Pd2Ga, Chin. Phys. B, 2012, 21, 037101 CrossRef.
- Q. J. Liu, Z. T. Liu and L. P. Feng, First-Principles Calculations of Structural, Elastic and Electronic Properties of Tetragonal HfO2 under Pressure, Commun. Theor. Phys., 2011, 56, 779–784 CrossRef CAS.
- R. Stadler, W. Wolf, R. Podloucky, G. Kresse, J. Furthmller and J. Hafner, ab initio calculations of the cohesive, elastic, and dynamical properties of CoSi2 by pseudo potential and all-electron techniques, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1729 CrossRef CAS.
- A. H. Reshak and M. Jamal, Calculation of lattice constant of hexagonal compounds with two dimensional search of equation of state and with semilocal functionals a new package (2D-optimize), J. Alloys Compd., 2013, 555, 362–366 CrossRef CAS PubMed.
- 2Doptimize package is provided by M. Jamal as part of the commercial code WIEN2K, http://www.wien2k.at/.
- D. C. Wallace, Solid State Phys., 1970, 25, 301 CAS.
- M. Jamal, 2012, Hex-elastic, http://www.wien2k.at/reg_user/unsupported.
- M. Voigt, Lehrbuch der Kristallphysik, Taubner, Leipzig, 1928 Search PubMed.
- A. Reuss, Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle, Z. Angew. Math. Mech., 1929, 9, 49–58 CrossRef CAS.
- R. Hill, The Elastic Behavior of a Crystalline Aggregate, Proc. Phys. Soc., 1952, 65, 349 CrossRef.
- V. I. Anisimov and O. Gunnarsson, Density-functional calculation of effective Coulomb interactions in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 7570 CrossRef CAS.
- G. K. H. Madsen and P. Novák, An LDA + U study Charge order in magnetite, Europhys. Lett., 2005, 69, 777–783 CrossRef CAS.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2K, Karlheinz Schwarz, Techn. Universitat, Wien, Austria, 2001, ISBN 3-9501031-1-2 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 78, 3865 CrossRef.
- P. Haas, F. Tran and P. Blaha, Calculation of the lattice constant of solids with semilocal functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085104 CrossRef.
- Y. Zhao and D. G. Truhlar, Comment on More accurate generalized gradient approximation for solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 197101 CrossRef.
- M. J. Mehl and D. A. Papaconstantopoulos, Applications of a tight-binding total-energy method for transition and noble metals: Elastic constants, vacancies,
and surfaces of monatomic metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 4519 CrossRef CAS.
- C. Kittel, Introduction to Solid State Physics, Wiley, New York, 1976 Search PubMed.
- J. Donohue, The Structures of the Elements, Wiley, New York, 1974, pp. 191–199 Search PubMed.
- H. W. L. Alves, Ab initio calculations of the vibrational modes of MnAs and Ga1–xMnxAs, AIP Conf. Proc., 2007, 893, 151–152 CrossRef CAS PubMed.
- I. Rungger and S. Sanvito, Ab initio study on the magnetostructural properties of MnAs, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 024429 CrossRef.
- A. Waśkowska, et al. Thermoelastic properties of ScB2, TiB2, YB4 and HoB4: Experimental and theoretical studies, Acta Mater., 2011, 59, 4886–4894 CrossRef PubMed.
- G. Levchenko, et al. Preparation and some properties of ScB2 single crystals, J. Solid State Chem., 2006, 179, 2949–2953 CrossRef CAS PubMed.
- I. R. Shein and A. L. Ivanovskii, Elastic properties of mono- and polycrystalline hexagonal AlB2-like diborides of s, p and d metals from first-principles calculations, J. Phys.: Condens. Matter, 2008, 20, 415218 CrossRef.
- W. Obrowski, Naturwissenschaften, 1961, 48, 428 CrossRef CAS.
- C. Musa, R. Orrù, R. Licheri and G. Cao, On the controversial formation of silver diboride: processing of Ag + 2B powders by spark plasma sintering, Phys. C, 2009, 469, 1991–1995 CrossRef CAS PubMed.
- A. Yazdani, Comment and calculation on duality exchange in Gd2In, J. Appl. Phys., 2005, 97, 10B113 CrossRef PubMed.
- V. Singh, A. Bhattacharyya, S. Majumdar and I. Dasgupta, A theoretical and experimental study of magnetism in Gd2In, J. Appl. Phys., 2012, 111, 053709 CrossRef PubMed.
- R. F. S. Hearmon, in Landolt–Bórnstein Numerical Data and Functional Relationships in Science and Technology New Series, ed. K.-H. Hellwege and A. M. Hellwege, Springer, Berlin, 3rd/11th edn, 1979 Search PubMed.
- R. F. S. Hearmon, in Landolt–Bórnstein Numerical Data and Functional Relationships in Science and Technology New Series, ed. K.-H. Hellwege and A. M. Hellwege, Springer, Berlin, 3rd/18th edn, 1984 Search PubMed.
- ASM Handbook Committee, Properties of pure metal, ASM Handbook, Properties and Selection: Nonferrous Alloys and Special-Purpose Materials, ASM International, 1990, vol. 2, pp. 1099–1201 Search PubMed.
- C. Enss and S. Hunklinger, Low temperature Physics, Springer, Berlin, 2005 Search PubMed.
- C. Kittel, Introduction to Solid State Physics, John Wiley and Sons, Inc, New York, 7th edn, 1996 Search PubMed.
- R. G. Leisure, R. B. Schwarz, A. Migliori and M. Lei, Room-Temperature Elastic Constants of Sc and ScD0.18, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 1276–1279 CrossRef CAS.
- D. Tromans, Elastic anisotropy of HCP metal crystals and polycrystals, IJRRAS, 2011, 6(4), 462–483 Search PubMed.
- L. Fast, J. M. Wills, B. Johansson and O. Eriksson, Elastic constants of hexagonal transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51(24), 17431–17438 CrossRef CAS.
- C. E. Hu, Z. Y. Zeng, L. Zhang, X. R. Chen, L. C. Cai and D. Alfè, Theoretical investigation of the high pressure structure, lattice dynamics, phase transition, and thermal equation of state of titanium metal, J. Appl. Phys., 2010, 107, 093509 CrossRef PubMed.
- G. Simmons and H. Wang, Single Crystal Elastic Constants and Calculated Aggregate Properties: A Handbook, MIT Press, Cambridge, 2nd edn, 1971 Search PubMed.
- Y. J. Hao, L. Zhang, X. R. Chen, Y. H. Li and H. L. He, Phase transition and elastic constants of zirconium from first-principles calculations, J. Phys.: Condens. Matter, 2008, 20, 235230 CrossRef PubMed.
- E. Clouet, J. M. Sanchez and C. Sigli, First principles study of the solubility of Zr in Al, Phys Rev B, 2002, 65, 094105 CrossRef.
- H. Ikehata, N. Nagasako, T. Furuta, A. Fukumoto, K. Miwa and T. Saito, First-principles calculations for development of low
elastic modulus Ti alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 174113 CrossRef.
- I. Schnell, M. D. Jones, S. P. Rudin and R. C. Albers, Tight-binding calculations of the elastic constants and phonons of hcp Zr: complications due to anisotropic stress and long-range forces, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 054104 CrossRef.
- D. J. Oh and R. A. Johnson, Relationship between c/a ratio and point defect properties in HCP metals, J. Nucl. Mater., 1989, 169, 5–8 CrossRef CAS.
- Y. M. Kim, B. J. Lee and M. I. Baskes, Modified embedded-atom method interatomic potentials for Ti and Zr, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 014101 CrossRef.
- M. I. Baskes and R. A. Johnson, Modified embedded atom potentials for HCP metals, Modell. Simul. Mater. Sci. Eng., 1994, 2, 147 CrossRef CAS.
- E. A. Brandes and G. B. Brook, Smithells Metals Reference Book, Butterworth, London, 1983 Search PubMed.
- G. R. Love, C. C. Koch, H. L. Whaley and Z. R. McNutt, Elastic moduli and Debye temperature of polycrystalline technetium by ultrasonic velocity measurements, J. Less-Common Met., 1970, 20, 73–75 CrossRef CAS.
- D. Singh and Y. P. Yarshni, X-ray Debye temperature for hexagonal crystals, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1982, 38, 854–858 CrossRef.
- J. J. Gilman and B. W. Roberts, Elastic Constants of TiC and TiB2, J. Appl. Phys., 1961, 32, 1405 CrossRef CAS PubMed.
- P. S. Spoor, J. D. Maynard, M. J. Pan, D. J. Green, J. R. Hellmann and T. Tanaka, Elastic constants and crystal anisotropy of titanium diboride, Appl. Phys. Lett., 1997, 70, 1959 CrossRef CAS PubMed.
- S. J. Wright, Estimation of single-crystal elastic constants from textured polycrystal measurements, J. Appl. Crystallogr., 1994, 27, 794–801 CrossRef CAS.
- H. Ledbetter and T. Tanaka, Elastic-Stiffness Coefficients of Titanium Diboride, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 333–339 CrossRef.
- H. Y. Yan, Q. Wei, S. M. Chang and P. Guo, A first-principle calculation of structural, mechanical and electronic properties of titanium borides, Trans. Nonferrous Met. Soc. China, 2011, 21, 1627–1633 CrossRef CAS.
- S. K. Kwon, B. J. Min, S. J. Youn and K. S. Kim, Electronic Structures of Diboride Compounds: AgB2 and AuB2, J. Korean Phys. Soc., 2005, 46, L1295–L1298 CAS.
- R. Tomita, H. Koga, T. Uchiyama and I. Iguchi, Superconductivity in Silver Boron Intermetallic Compound, J. Phys. Soc. Jpn., 2004, 73, 2639–2641 CrossRef CAS.
- A. K. M. A. Islam, F. Parvin, F. N. Islam, M. N. Islam, A. T. M. N. Islam and I. Tanaka, AgB2: superconductivity and the role of paramagnons, Phys. C, 2007, 466, 76–81 CrossRef CAS PubMed.
- T. Oguchi, Cohesion in AlB2-Type Diborides: A First-Principles Study, J. Phys. Soc. Jpn., 2002, 71, 1495–1500 CrossRef CAS.
- F. Yang, R. S. Han, N. H. Tong and W. Guo, Electronic Structural Properties and Superconductivity of Diborides in the MgB2 Structure, Chin. Phys. Lett., 2002, 19, 1336–1339 CrossRef.
- H. B. Ozisik, K. Colakoglu and E. Deligoz, First-principles study of structural and mechanical properties of AgB2 and AuB2 compounds under pressure, Comput. Mater. Sci., 2012, 51, 83–90 CrossRef CAS PubMed.
- M. Dörfler and K. Blrnert, The Elastic Constants of MnAs, Phys. Status Solidi A, 1973, 17, 141–148 CrossRef.
- I. S. Grigoriev and E. Z. Meilikhov, Handbook of Physical Quantities, CRC, Boca Raton, 1997 Search PubMed.
- X. Q. Chen, H. Niu, D. Li and Y. Li, Modeling hardness of polycrystalline materials and bulk metallic glasses, Intermetallics, 2011, 19, 1275–1281 CrossRef CAS PubMed.
- H. Niu, X. Q. Chen, P. Liu, W. Xing, X. Cheng, D. Li and Y. Li, Extra-electron induced covalent strengthening and generalization of intrinsic ductile-to-brittle criterion, Sci. Rep, 2012, 2(718), 1–6 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.  changes. Elastic constants link the stress to strain and distinguish the elastic and plastic regimes due to the elastic stability criteria. In turn, these parameters can describe the response of crystals to external forces on solid materials by using first principle calculations1–8 due to their technological important properties such as stiffness, hardness, and brittle/ductility. Moreover, other mechanical properties such as Voigt, Reuss, and Hill bulk moduli, shear and Young's moduli as well as Poisson's ratio3,9 are estimated from elastic coefficients. They also make a connection with thermodynamical properties such as transverse and longitudinal sound velocities, specific heat, Debye temperature, and melting point.9 In addition, based on the calculated elastic constants, we are able to define the elastic anisotropy ratio, which is an important physical quantity for the structural phase stability of crystal structures.9 Based on these evidences one can conclude that the calculation of elastic constants for solid materials, is very attractive and important. Therefore, elastic constants can be the physical quantities for evaluating of accuracy and validity for the employed methods, thus the elastic constants can be a level of accuracy for the employed method, especially based on density functional theory (DFT), one of the most accurate schemes for the band structure calculations.
changes. Elastic constants link the stress to strain and distinguish the elastic and plastic regimes due to the elastic stability criteria. In turn, these parameters can describe the response of crystals to external forces on solid materials by using first principle calculations1–8 due to their technological important properties such as stiffness, hardness, and brittle/ductility. Moreover, other mechanical properties such as Voigt, Reuss, and Hill bulk moduli, shear and Young's moduli as well as Poisson's ratio3,9 are estimated from elastic coefficients. They also make a connection with thermodynamical properties such as transverse and longitudinal sound velocities, specific heat, Debye temperature, and melting point.9 In addition, based on the calculated elastic constants, we are able to define the elastic anisotropy ratio, which is an important physical quantity for the structural phase stability of crystal structures.9 Based on these evidences one can conclude that the calculation of elastic constants for solid materials, is very attractive and important. Therefore, elastic constants can be the physical quantities for evaluating of accuracy and validity for the employed methods, thus the elastic constants can be a level of accuracy for the employed method, especially based on density functional theory (DFT), one of the most accurate schemes for the band structure calculations.
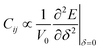 . Usually for hexagonal compounds with two degrees of freedom, EOS is calculated with constant
. Usually for hexagonal compounds with two degrees of freedom, EOS is calculated with constant 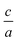 ratio (1D-search of EOS) while in our research to find the elastic constants of hexagonal compounds, we are interested to improve the method of search for evaluation EOS and calculate the optimized volume with 2D-search of EOS.11 In this regards, we use 2D optimize package12 and apply the appropriate exchange–correlation functional. To overcome the deficiency of DFT for the compounds with localized electrons, we apply PBE + U approximation using our calculated U parameter.
ratio (1D-search of EOS) while in our research to find the elastic constants of hexagonal compounds, we are interested to improve the method of search for evaluation EOS and calculate the optimized volume with 2D-search of EOS.11 In this regards, we use 2D optimize package12 and apply the appropriate exchange–correlation functional. To overcome the deficiency of DFT for the compounds with localized electrons, we apply PBE + U approximation using our calculated U parameter.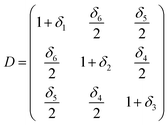


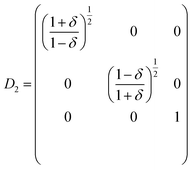
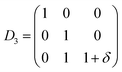




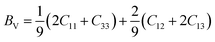










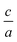 structure optimization by using 2Doptimize package12 for hexagonal compounds. That means to find the optimized lattice parameters (a and c) we have performed at least 25 self-consistent calculations.
structure optimization by using 2Doptimize package12 for hexagonal compounds. That means to find the optimized lattice parameters (a and c) we have performed at least 25 self-consistent calculations.
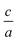 ratio, then we select a set of
ratio, then we select a set of 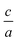 changes and then by using the following equation:
changes and then by using the following equation: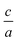 ratio, respectively) we find the best
ratio, respectively) we find the best 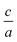 ratio for each volume in the way that the energy has minimum value.
ratio for each volume in the way that the energy has minimum value.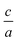 ratio and then by using the included supported equation of states, i.e. EOS2, Murnaghan and Brich–Murnaghan, the minimum total energy and the equilibrium volume are calculated.
ratio and then by using the included supported equation of states, i.e. EOS2, Murnaghan and Brich–Murnaghan, the minimum total energy and the equilibrium volume are calculated.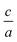 ratio at the equilibrium volume, 2Doptimize package fits the optimized
ratio at the equilibrium volume, 2Doptimize package fits the optimized 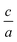 ratios for each volume on the polynomial.
ratios for each volume on the polynomial. ratio and volume, respectively.
ratio and volume, respectively.
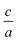 ratio at the optimized volume, by using the above equation.
ratio at the optimized volume, by using the above equation.
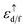 and εF are the spin up eigenvalue of localized electron (d or f electrons) and Fermi energy, respectively, the spin up eigenvalue, are weighted as a function of spin up relativistic quantum number. The calculated effective Hubbard U parameter for MnAs, Gd, Gd2In and Tb compounds were listed in Table 1.
and εF are the spin up eigenvalue of localized electron (d or f electrons) and Fermi energy, respectively, the spin up eigenvalue, are weighted as a function of spin up relativistic quantum number. The calculated effective Hubbard U parameter for MnAs, Gd, Gd2In and Tb compounds were listed in Table 1.
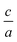 structure optimization, is important. As one can see from Fig. 1, 2D-search of EOS, predicts the smaller optimized volume and lower energy rather than 1D-search of EOS for Tm metal, which is consistent with experimental volume.11
structure optimization, is important. As one can see from Fig. 1, 2D-search of EOS, predicts the smaller optimized volume and lower energy rather than 1D-search of EOS for Tm metal, which is consistent with experimental volume.11


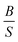 ratio is less (more) than 1.75.8 The sign of Cauchy pressure (C12 − C55) can be used to predict the type of bonds. Usually, the Cauchy pressure of compounds with more dominant covalent (ionic) bonds is negative (positive).7 On the other hand, the value of Poisson's ratio can be used to predict the type of bonds. Stiffness is resistance to deformation forces. Young's modulus, as the ratio of stress and strain, is representative of the stiffness. It means that the greater the value of Young's modulus (E), the stiffer the material is. Hardness is related to how much the material is resistant to the shape changes. There are two representatives for it; (i) bulk modulus, which is related to the resistance against the volume changes and (ii) shear modulus, which is related to the resistance against the reversible deformations. Therefore, it is clear that shear modulus can be a better predictor for hardness.8
ratio is less (more) than 1.75.8 The sign of Cauchy pressure (C12 − C55) can be used to predict the type of bonds. Usually, the Cauchy pressure of compounds with more dominant covalent (ionic) bonds is negative (positive).7 On the other hand, the value of Poisson's ratio can be used to predict the type of bonds. Stiffness is resistance to deformation forces. Young's modulus, as the ratio of stress and strain, is representative of the stiffness. It means that the greater the value of Young's modulus (E), the stiffer the material is. Hardness is related to how much the material is resistant to the shape changes. There are two representatives for it; (i) bulk modulus, which is related to the resistance against the volume changes and (ii) shear modulus, which is related to the resistance against the reversible deformations. Therefore, it is clear that shear modulus can be a better predictor for hardness.8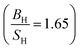 result show that the Sc is a brittle material, however this value is near to 1.75, while experiments predict that it behaves as a ductile
result show that the Sc is a brittle material, however this value is near to 1.75, while experiments predict that it behaves as a ductile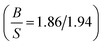 . This inconsistency can be considered from the fact that our calculations are at zero temperature, while the experiments are at 303 K. Therefore, our PBE calculations result shows that the Sc behaves as an IBH4S4 material at zero-temperature. Future experimental work will testify our calculated results.
. This inconsistency can be considered from the fact that our calculations are at zero temperature, while the experiments are at 303 K. Therefore, our PBE calculations result shows that the Sc behaves as an IBH4S4 material at zero-temperature. Future experimental work will testify our calculated results.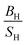 ratio (1.56) and experimental value (1.63), suggest that Ru behaves as a brittle material. The present value of Young's and shear moduli are high, therefore it is suggested that Ru is stiffer and hardness. These results within WC exchange–correlation, suggest that Ru should be considered as a CBH12S12 material, while the Poisson's ratio 0.236 (see ref. 31 and reference therein) predicts that Ru exhibit ionic bonding which is consistent with the experimental elastic constants prediction. The elastic constants of Os along with previous theoretical calculations are listed in Table 5. Our results within WC exchange–correlation are in reasonable agreement with previous calculations.42,43 However, our calculated C55 is 312.7 GPa, while the previous calculated value was 162.2 GPa.43 This difference leads to the different signs of Cauchy pressure (C12 − C55) for our results than the previous calculations.43 Therefore, our (previous43) results predict that covalent (ionic) bonds are more dominant for Os compound, while the Poisson's ratio 0.221 (see ref. 31 and reference therein) predicts that Os exhibit ionic bonding.
ratio (1.56) and experimental value (1.63), suggest that Ru behaves as a brittle material. The present value of Young's and shear moduli are high, therefore it is suggested that Ru is stiffer and hardness. These results within WC exchange–correlation, suggest that Ru should be considered as a CBH12S12 material, while the Poisson's ratio 0.236 (see ref. 31 and reference therein) predicts that Ru exhibit ionic bonding which is consistent with the experimental elastic constants prediction. The elastic constants of Os along with previous theoretical calculations are listed in Table 5. Our results within WC exchange–correlation are in reasonable agreement with previous calculations.42,43 However, our calculated C55 is 312.7 GPa, while the previous calculated value was 162.2 GPa.43 This difference leads to the different signs of Cauchy pressure (C12 − C55) for our results than the previous calculations.43 Therefore, our (previous43) results predict that covalent (ionic) bonds are more dominant for Os compound, while the Poisson's ratio 0.221 (see ref. 31 and reference therein) predicts that Os exhibit ionic bonding.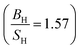 predicts that it is more brittle than PBE approximation
predicts that it is more brittle than PBE approximation 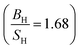 . The higher value of shear modulus within PBE + U approximation indicates that Gd is harder than that obtained within PBE approximation. The higher value of Young's modulus with Hubbard U correction indicates that Gd is stiffer than that obtained within PBE prediction. Therefore, comparing the results of PBE + U approximation for Gd with results of other compounds within different exchange–correlation, indicate Gd as an IBH1S1 material. According to Table 6 (Tb compound) we can observe that PBE + U approximation improves the obtained elastic constants towards the experimental data.39,42,55 Concerning the changes of other parameters, we obtain that the effect of Hubbard U parameter is so important for Tb (see Table 6). The effective Hubbard U parameter changes the order of C12 > C55 (PBE) to C12 < C55 (PBE + U). This means that PBE exchange–correlation predicts that ionic bonds are more dominant for Tb, while Hubbard U correction (PBE + U approximation) changes it from ionic to covalent bonds.
. The higher value of shear modulus within PBE + U approximation indicates that Gd is harder than that obtained within PBE approximation. The higher value of Young's modulus with Hubbard U correction indicates that Gd is stiffer than that obtained within PBE prediction. Therefore, comparing the results of PBE + U approximation for Gd with results of other compounds within different exchange–correlation, indicate Gd as an IBH1S1 material. According to Table 6 (Tb compound) we can observe that PBE + U approximation improves the obtained elastic constants towards the experimental data.39,42,55 Concerning the changes of other parameters, we obtain that the effect of Hubbard U parameter is so important for Tb (see Table 6). The effective Hubbard U parameter changes the order of C12 > C55 (PBE) to C12 < C55 (PBE + U). This means that PBE exchange–correlation predicts that ionic bonds are more dominant for Tb, while Hubbard U correction (PBE + U approximation) changes it from ionic to covalent bonds.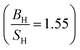 predicts that Gd2In is more brittle than PBE + U prediction
predicts that Gd2In is more brittle than PBE + U prediction 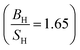 . The higher value of Young's modulus with Hubbard U parameter makes Gd2In stiffer than PBE prediction. PBE and PBE + U approximations predict that ionic bonds are more dominant for Gd2In (C12 > C55), i.e. the prediction of PBE and PBE + U about type of bonds are the same. Thus, in this research Gd2In behaves as an CBH5S5 material.
. The higher value of Young's modulus with Hubbard U parameter makes Gd2In stiffer than PBE prediction. PBE and PBE + U approximations predict that ionic bonds are more dominant for Gd2In (C12 > C55), i.e. the prediction of PBE and PBE + U about type of bonds are the same. Thus, in this research Gd2In behaves as an CBH5S5 material.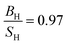 ratio show that TiB2 behaves as a brittle material, which is consistent with experimental prediction and better than previous calculations. The high value of Young's and shear moduli, define TiB2 as a stiff and hard material. Therefore, in this research, TiB2 behaves as a CBH13S13 material within PBE.
ratio show that TiB2 behaves as a brittle material, which is consistent with experimental prediction and better than previous calculations. The high value of Young's and shear moduli, define TiB2 as a stiff and hard material. Therefore, in this research, TiB2 behaves as a CBH13S13 material within PBE.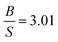 66 for AgB2 compound which is more ductile than our calculation
66 for AgB2 compound which is more ductile than our calculation 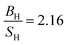 . The comparison of Young's modulus between Ozisik66 and our calculations, demonstrate that AgB2 is stiffer than our calculations. Therefore, our results within PBE suggest that AgB2 is an IDH9S9 material. These differences can be considered from the fact that our calculations are using lattice parameters from 2D-search. Future experimental work will testify our calculated results. The obtained ferromagnetic-results of MnAs, along with experimental data in the paramagnetic state at 303 K (ref. 67) for seeking comparison, are given in Table 8. The effect of Hubbard U parameter, changes the order of elastic constants from C12 < C13 < C55 < C11 < C33 to C13 < C12 < C55 < C33 < C11 when we move from PBE → PBE + U. It is observed that PBE + U approximation, improves the obtained bulk modulus toward experimental values.68 The Hubbard U correction does not change the prediction of Cauchy pressure (C12 − C55) and Poisson's ratio regarding the type of bonds. Both of PBE and PBE + U predict ionic bonds are more dominate for MnAs compound (C12 > C55). Hubbard U correction makes MnAs more brittle than PBE prediction. PBE + U approximation predicts that MnAs is more hard (see the value of shear modulus in Table 8) than PBE prediction. The higher value of Young's modulus within PBE + U approximation, predicts that MnAs is stiffer than the PBE prediction. Therefore, in this work we recognize MnAs as a CBH8S7 material.
. The comparison of Young's modulus between Ozisik66 and our calculations, demonstrate that AgB2 is stiffer than our calculations. Therefore, our results within PBE suggest that AgB2 is an IDH9S9 material. These differences can be considered from the fact that our calculations are using lattice parameters from 2D-search. Future experimental work will testify our calculated results. The obtained ferromagnetic-results of MnAs, along with experimental data in the paramagnetic state at 303 K (ref. 67) for seeking comparison, are given in Table 8. The effect of Hubbard U parameter, changes the order of elastic constants from C12 < C13 < C55 < C11 < C33 to C13 < C12 < C55 < C33 < C11 when we move from PBE → PBE + U. It is observed that PBE + U approximation, improves the obtained bulk modulus toward experimental values.68 The Hubbard U correction does not change the prediction of Cauchy pressure (C12 − C55) and Poisson's ratio regarding the type of bonds. Both of PBE and PBE + U predict ionic bonds are more dominate for MnAs compound (C12 > C55). Hubbard U correction makes MnAs more brittle than PBE prediction. PBE + U approximation predicts that MnAs is more hard (see the value of shear modulus in Table 8) than PBE prediction. The higher value of Young's modulus within PBE + U approximation, predicts that MnAs is stiffer than the PBE prediction. Therefore, in this work we recognize MnAs as a CBH8S7 material.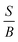 ratio (Pugh's modulus, it can define as
ratio (Pugh's modulus, it can define as 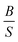 (ref. 8 and 31)) and revised Cauchy pressure
(ref. 8 and 31)) and revised Cauchy pressure 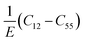 (E-Young modulus) are well correlated to a hyperbolic criterion to recognize the ductile to brittle properties for a large materials of cubic symmetry. This means that there is a correlation between ductility/brittle and metallic/covalent concepts.70 We could find (see Fig. 6) this correlation between ductility/brittle and ionic/covalent concepts for our hexagonal compounds except for Sc, Y, Gd, and Gd2In at zero temperature (PBE + U results were used) which for them our results predict brittle materials and ionic bonds. However, using the mechanism proposed by the previous analysis70 these materials are not exceptions. From Fig. 6, we can see that the Sc, Y, Gd and Gd2In are close to the transformation zone. So, we realize that the mechanism proposed in the previous report70 can be also suitable for the hexagonal compounds.
(E-Young modulus) are well correlated to a hyperbolic criterion to recognize the ductile to brittle properties for a large materials of cubic symmetry. This means that there is a correlation between ductility/brittle and metallic/covalent concepts.70 We could find (see Fig. 6) this correlation between ductility/brittle and ionic/covalent concepts for our hexagonal compounds except for Sc, Y, Gd, and Gd2In at zero temperature (PBE + U results were used) which for them our results predict brittle materials and ionic bonds. However, using the mechanism proposed by the previous analysis70 these materials are not exceptions. From Fig. 6, we can see that the Sc, Y, Gd and Gd2In are close to the transformation zone. So, we realize that the mechanism proposed in the previous report70 can be also suitable for the hexagonal compounds.

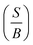 seems to mirror the hardness of materials i.e. hardness increases with increasing Pugh's modulus. For example, the ordering of hardness using shear modulus for Ru and Os will be as Ru, Ti2B, Os while from Fig. 6, using Pugh's modulus, it will be as Ru, Os. In the above, we completed this discussion using Vickers hardness.
seems to mirror the hardness of materials i.e. hardness increases with increasing Pugh's modulus. For example, the ordering of hardness using shear modulus for Ru and Os will be as Ru, Ti2B, Os while from Fig. 6, using Pugh's modulus, it will be as Ru, Os. In the above, we completed this discussion using Vickers hardness.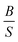 ratio (to predict brittle/ductility of materials) trend. This can again emphasize that there is a correlation between type of bonds and brittle/ductility of materials.
ratio (to predict brittle/ductility of materials) trend. This can again emphasize that there is a correlation between type of bonds and brittle/ductility of materials.

