Reusable colloidal graphene oxide suspensions combined with dialysis bags for recovery of trace Y(III) from aqueous solutions

Abstract

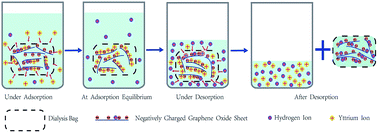
Recycling trace rare earth elements (REEs) from effluents from mines and refineries is vital for the protection of the global environment and utilization of valuable REE resources. In this work, a novel and highly efficient method for second-pollution-free adsorptive recovery of trace Y(III) from aqueous solutions by colloidal graphene oxide (GO) suspensions loaded in dialysis bags has been developed based on the properties of GO suspensions and the sieving characteristics of dialysis membranes. The effects of pH, ionic strength and temperature on Y(III) adsorption–desorption on GO were studied. Thermodynamic and kinetic investigations on Y(III) adsorption on GO were also conducted. The maximum adsorption capacity of Y(III) on GO at pH = 5.9 ± 0.1 and T = 303 K was 190.48 mg g⁻¹, higher than any other adsorbents reported so far. In the fourth consecutive adsorption–desorption cycle, the Y(III)-saturated GO suspension was still able to resume a colloidal state in pH = 0.9 HNO₃ aqueous solution with a desorption rate of 74.26% while the regenerated GO maintained an adsorption capacity of 138.73 mg g⁻¹. The adsorption–desorption capacities of Y(III) on GO depended more on pH than on ionic strength and temperature. The studies on adsorption thermodynamics and kinetics showed that the adsorption of Y(III) on GO was an endothermic, spontaneous and monolayer adsorption process, and perfectly fitted the Langmuir model and the pseudo-second-order model. In summary, GO is a highly efficient and easily reusable adsorbent with promising application for the treatment of industrial wastewater and the enrichment and recovery of lanthanides. More importantly, the combination of colloidal GO suspension with dialysis membrane facilely avoids the re-pollution of the treated solutions, drastically reduces workload in separation and recovery of GO and provides an alternative route for actual application of nano-sized adsorbents in environmental pollutant removal and valuable resource recovery from wastewater.

---

1. Introduction

Over the past three decades, global reserves of rare earth elements (REEs) have been declining quickly and drastically growing amounts of REEs have been released into the environment and exposed to humans owing to more and more widespread use of REEs in high-technology industries.¹ Especially in the surrounding areas of weathered crust elution-deposited REE mines and refineries in southern China, effluents from in situ leaching mining and indiscriminate discharge of industrial wastewater not only severely pollute surface water and ground water and threaten the health of the local inhabitants, but also cause huge loss of ionic state REEs.² Although REE concentrations in these wastewaters are as low as one to hundreds of mg L⁻¹, more than 7.2 million tons of such wastewater are generated and discharged annually due to lack of effective recovery techniques.³ Hence, highly efficient enrichment and recovery of REEs from wastewater is an urgent task for the protection of human health and the environment as well as for full utilization of REE resources.

Various methods for the recovery and removal of REE ions from wastewater have been developed, including adsorption,⁴ membrane separation,⁵ precipitation,⁶ etc. Among these techniques, adsorption is regarded as a simple, economic and efficient approach especially for the separation of trace REE ions.^7,8 It is reported that adsorbents such as by-pass cement dust,⁴ activated carbon,⁹ γ-Al₂O₃,¹⁰ bacterial cell walls,¹¹ polyethyleneglycol (phosphomolybdate and tungstate) heteropolyacid,¹² etc., could be applied in the removal of REE ions from water.

In the past decade, graphene, a newly emerging two-dimensional nanomaterial, has attracted enormous worldwide scientific interest of researchers and promises potential applications in a variety of areas owing to a range of unique and prominent properties. Application of graphene, chemically modified graphene and graphene-based nanocomposites in environmental clear-up is one of the hot-spots in present research.¹³ In addition to high specific surface area, graphene oxide (GO) is the most common chemically modified graphene with a range of abundant oxygen-containing functional groups, such as epoxide, hydroxyl, carbonyl and carboxyl groups, which makes it hydrophilic and easy to disperse in water to form stable colloidal suspensions.^14,15 GO can be readily prepared by the well-established modified Hummers method using common flake graphite as raw material on an industrial scale and at an economic cost in the near future. Therefore, GO has become an ideal adsorbent for the removal of metal ions and organic pollutants from aqueous solutions. It was documented that GO had a higher adsorption capacity than any of today's adsorbents for the removal of Cu(II),¹⁶ Zn(II),¹⁶ Cd(II),^16,17 Co(II),¹⁷ Pb(II),^17,18 U(VI),¹⁹ Eu(III)²⁰ and Th(IV)²¹ from water. To enhance the adsorption properties for metal ions, numerous graphene-based nanocomposites have been synthesized by chemical modification of GO or attachment of nanoparticles to GO^22–25 However, as graphene-based adsorbents are usually dispersed into wastewater and form a stable colloid when used in wastewater treatment, there are a few troublesome problems restricting their application in real work to be confronted, i.e. difficult sedimentation and separation of the nanoadsorbents and huge filtration volume in their recovery and separation from treated wastewater after the adsorption process as well as regeneration of the nanoadsorbents. If not solved properly, re-pollution of the treated solutions will occur and the cost of industrial applications will be increased.²⁶

To separate GO from treated wastewater quickly and avoid re-pollution, major investigations have been focused on the synthesis of magnetite/GO nanocomposites by attaching magnetite nanoparticles to GO with a view to convenient magnetic separation.^24–29 Nevertheless, the attachment of magnetite nanoparticles to GO inevitably lessens unit weight adsorption capacity due to adding dead weight,²⁴ which is also confirmed by comparing published data.^16,29 It could be due to the fact that the nanoparticles may instead tie up adsorption sites, limiting adsorption capacity. Furthermore, the large-scale application of magnetic nanoparticles/GO hybrids in removing organic ions and inorganic pollutants from wastewater is still restricted by the synthetic complexity and high cost of the functional hybrids. In particular, the magnetic nanoparticles on the surface of GO tend to dissolve in strong acidic solutions, which greatly limits their application.²⁷

In the present work, we propose a facile and general strategy for adsorptive recovery of trace metal ions from wastewater by combining colloidal GO suspension with dialysis membrane, which promises widespread application in water purification and resource recycling due to no re-pollution of the treated solutions, convenient nanoadsorbent separation, and great reduction in separation workload and application cost. Taking Y(III) as a representative REE, which is the most abundant REE in the weathered crust elution-deposited rare earth mine in south China, the objectives of this study are to (a) test and verify the adsorptive recovery feasibility of trace Y(III) from aqueous solutions, using colloidal aqueous suspensions of GO loaded in dialysis bags; (b) study the effects of pH, ionic strength and temperature on Y(III) adsorption–desorption; (c) investigate the regenerability and reusability of Y(III)-saturated GO; and (d) deal with the thermodynamics and kinetics of Y(III) adsorption on colloidal GO.

2. Experimental

2.1 Materials

BIOSHARP regenerated cellulose dialysis bags with 8000–14 000 molecular weight cut-off and of 21 mm in diameter were purchased from Shanghai Treasure Biological Technology Co. Ltd and used after pretreatment in boiling deionized water for 3–5 min.

Colloidal GO suspension was synthesized using the modified Hummers method from flake graphite (purity: 99.95 wt%, particle size: 325 mesh, Xianfeng Nano Co. Ltd). Briefly, flake graphite was strongly oxidized by using KMnO₄ and concentrated H₂SO₄ under ultrasonication, and H₂O₂ was then added to eliminate the excess MnO₄⁻ anions. Subsequently, the purification processes such as rinsing with deionized water, centrifugal separation, ultrasonication and BIOSHARP membrane dialysis were repeated until the deionized water for dialysis was neutral. Thus the stock suspension of GO was obtained, whose concentration was determined by a gravimetric method. The GO suspensions for ion adsorption were prepared by dilution according to the experimental requirements. A Y(III) aqueous standard solution at 12 mg L⁻¹ was prepared by dissolving Y₂O₃ (purity 99.999 wt%) in nitric acid and followed by heating until the excess nitric acid was evaporated. The detailed processes are described in the ESI.†

2.2 Characterization of GO

GO was characterized by transmission electron microscopy (TEM), atomic force microscopy (AFM), powder X-ray diffraction (XRD), Raman spectroscopy and Fourier transform infrared (FT-IR) spectroscopy. The TEM images were obtained with a JEOL transmission electron microscope (JEM-2100, Japan). The AFM images were obtained in air using a Digital Instruments Nanoscope III in tapping mode. The XRD patterns were measured using an Advance D8 diffractometer with Cu-Kα radiation. The Raman spectrum was recorded with a JobinYvon Lab Ram HR800 spectrometer at room temperature. The FT-IR spectroscopy measurement was conducted by using a Nicolet 5700 spectrometer with samples in KBr pellets. The zeta potentials of 100 mg L⁻¹ colloidal aqueous GO suspensions as a function of pH were measured by a Zetatrac dynamic light scattering detector (Microtrac Limited Corp., USA) at 303 K.

2.3 Batch adsorption experiments

In the adsorption experiments, 10 mL of a 100 mg L⁻¹ (pH = 5.9 ± 0.1) colloidal GO suspension was sealed into a dialysis bag to constitute an adsorption unit. The batch adsorption experiments of Y(III) on GO nanosheets in colloidal suspensions were carried out by immersing an adsorption unit in 25 mL of 12 mg L⁻¹ Y(III) aqueous solutions in a large-mouth conical flask placed in a water-bathing thermostatic shaker. Two aliquot parts of the treated solutions were sampled at regular intervals to determine Y(III) concentrations by a visible adsorption spectrophotometric method using arsenazo-III as the chromogenic agent at a wavelength of 656 nm. The average of duplicate determinations with relative errors below 5% was the Y(III) concentration of the treated solution. The amounts of Y(III) adsorbed by the colloidal GO suspensions were calculated from the differences between the initial concentration (C₀, mg L⁻¹) and equilibrium one (C_e, mg L⁻¹).

Adsorption capacity:

q_e = [(V_sC₀ − (V_s + V_g)C_e]/M

where q_e is the equilibrium adsorption capacity of Y(III) on the GO (mg g⁻¹), V_s and V_g are the volumes of the treated solution and colloidal GO suspension (L), respectively, and M is the mass of the GO (g).

As the pH of common wastewater from REE mines and refineries is usually about 6.0, all the adsorption experiments were conducted at 303 K, using pH = 5.9 ± 0.1 Y(III) solution and GO suspension in the dialysis bag unless specified otherwise. For the experiments of pH effect, the initial pH of the Y(III) aqueous solution to be treated was adjusted to be in the range of 2.0–11.0 by adding negligible volume of 0.1 or 0.05 mol L⁻¹ HNO₃ or NaOH solution. It was noted that the pH of the Y(III) solution was <7.86 during the adsorption process and that no Y(III) precipitation occurred in the aqueous solution. For the experiments of ionic strength effect, NaClO₄ was added to achieve Y(III) solutions containing the desired NaClO₄ concentrations.

2.4 Desorption and regeneration study

For the desorption study, 10 mL of a 100 mg L⁻¹ (pH = 5.9 ± 0.1) colloidal GO suspension was sealed into a dialysis bag to constitute an adsorption unit. Then the adsorption unit was immersed into 25 mL of Y(III) solutions with initial concentration of 12.0 mg L⁻¹, and was kept in a water-bathing thermostatic shaker at 303 K for 25 min. Two aliquot parts of each treated solution were sampled to determine Y(III) concentrations. Finally, Y(III)-saturated adsorption units were soaked in 25 mL of 0.1 M HNO₃ aqueous solutions and vibrated for 60 min. After desorption, two aliquot parts of each treated solution were sampled to determine Y(III) concentrations, using a spectrophotometric determination method. The desorption capacity and desorption rate of Y(III)-saturated GO were calculated according to the following equations:

Desorption rate:

R_d = V_dC_d/q_eM

where C_d is the concentration of Y(III) in the desorption solution (mg L⁻¹), M is the mass of the GO (g), V_d and V_s are the volumes of the desorption solution and Y(III)-saturated GO suspension (L), respectively, and q_e is the equilibrium adsorption capacity of Y(III) on the GO (mg g⁻¹), which is calculated by the following equation: q_e = [(V_sC₀ − (V_s + V_g)C_e]/M.

3. Results and discussion

3.1 Characterization of GO

TEM, AFM, XRD, Raman and FT-IR characterizations of the prepared GO nanosheets and pH-dependent zeta potentials of the colloidal GO suspensions are presented in Fig. 1. The TEM image in Fig. 1a shows that crumpled flower-like GO nanosheets are formed, where the transparent areas indicate few layers of GO and the dark areas suggest the crumpled section of GO. From the AFM image in Fig. 1b, the GO nanosheets are of micrometer scale in lateral dimensions and about 0.947 nm in thickness, suggesting the presence of one-layered GO nanosheets. The thickness of a one-layer GO nanosheet is 0.8–1.0 nm.³⁰

Fig. 1 Characterization of GO nanosheets: (a) TEM image; (b) AFM image with a representative height profile; (c) XRD patterns of flake graphite and GO nanosheets; (d) Raman spectrum; (e) FT-IR spectrum; (f) zeta potentials of 100 mg L⁻¹ colloidal GO suspensions as a function of pH.

Fig. 1c presents XRD patterns of GO nanosheets and flake graphite. As Fig. 1c shows, the intense diffraction peak at 2θ = 26.40° (d = 0.335 nm) corresponding to the natural graphite spacing (002) of graphite planes disappears in the pattern of GO nanosheets while the relatively weak diffraction peak attributed to the (001) reflection of GO appears at around 2θ = 8.07° (d = 0.940 nm), lower than the reported diffraction angles due to the higher oxidation degree of GO.^31,32 Owing to the introduction of abundant oxygen-containing functional groups on the graphite sheets, the interlayer spacing increases from the 0.335 nm of pristine graphite to 0.940 nm of GO, which coincides well with the AFM measurement (0.947 nm).³³

In the Raman spectrum (Fig. 1d), the G band at ∼1580 cm⁻¹ is attributed to the vibration of sp² carbon atoms in a graphitic two-dimensional hexagonal lattice, and the D band at ∼1350 cm⁻¹ is associated with the vibrations of sp³ carbon atoms of defects and disorder. The weak and broad 2D peak at ∼2700 cm⁻¹ is an indication of disorder as the result of an out-of-plane vibration mode. These strong G, D, and 2D bands are in good agreement with previous results of GO characterization.³⁴

To identify the functional groups on the surfaces of the GO nanosheets, an FT-IR spectrum was recorded. As shown in Fig. 1e, the characteristic absorption peaks of several oxygen-containing groups are observed, including the broad and intense peak of O–H groups centered at 3430 cm⁻¹, the strong C–O–C peak around 1100 cm⁻¹, the 1401 cm⁻¹ peak arising from the bending vibration of C–O–H groups, and the peaks at 1716 cm⁻¹ and 1574 cm⁻¹, corresponding to C=O and C=C, respectively, which suggest that large amounts of oxygen-containing functional groups (hydroxyl, carboxyl, carbonyl, and epoxy groups) are present on the surface of GO.

As presented in Fig. 1f, in the pH range from 2 to 11, all the zeta potentials of as-prepared colloidal GO suspensions are negative, and become more negative with increasing pH value, indicating that these GO sheets are highly negatively charged when dispersed in water and become more stable in more basic solution. The results are consistent with a previous report.¹⁵

3.2 Effect of pH, ionic strength and temperature on adsorption–desorption of Y(III) on GO nanosheets

In Fig. 2a, the adsorption curve of Y(III) on GO nanosheets in colloidal suspensions as a function of Y(III) solution pH is presented as open triangles and log₁₀[Y³⁺][OH⁻]³ curve of the Y(III) solution to be adsorbed as a function of pH is displayed as filled squares. The adsorption capacity of Y(III) on GO nanosheets increases slowly at pH < 6, quickly at pH 6–8 and then remains over 270 mg g⁻¹ with lower rate of increase at pH > 8. From the results in Fig. 1f, all the zeta potentials of colloidal GO suspensions in the pH range from 2 to 11 are negative, and become more negative with increasing pH value, which is due to different degrees of ionization of the carboxylic acid and phenolic hydroxyl groups on the GO nanosheets as a function of pH value. Positive metal ions tend to be adsorbed on the negatively charged surface of GO nanosheets owing to electrostatic attraction. With increasing pH value, the zeta potentials are more negative and the electrostatic interactions between Y(III) and GO nanosheets become stronger, and thereby result in enhanced Y(III) adsorption. At lower pH values, some of the negatively charged functional groups are protonated with H⁺, and the bulk binding sites are occupied, so the GO adsorption capacity for Y(III) is decreased. According to the logarithmic value of precipitation constant log₁₀ K_sp[Y(OH)₃] = −22.76, it can be calculated from Fig. 2a that for C_[Y(III)] = 20 mg L⁻¹ aqueous solution, Y(III) begins to precipitate at pH ≥ 7.86 in the absence of 10 mL colloidal GO suspension with pH = 5.9 ± 0.1. The experimental results showed that the pH value of the pH = 11 solution after GO adsorption fell to 7.60, which is below the pH value of Y(III) precipitation (7.86). Therefore, when 10 mL of 100 mg L⁻¹ (pH = 5.9 ± 0.1) GO suspension in dialysis bag is used for treatment of Y(III) solutions with the pH ranging from 2.0 to11.0, for Y(III) solutions with pH < 7.86, most Y(III) ions are directly adsorbed by GO. For Y(III) solutions with pH ≥ 7.86, the formed Y(III) precipitates dissolve gradually to become Y(III) ions in the adsorption process, which are rapidly adsorbed by GO through micropores of the dialysis membrane.

Fig. 2 (a) Effect of pH on the adsorption of Y(III) on GO nanosheets in colloidal suspensions and log₁₀[Y³⁺][OH⁻]³ curve of the Y(III) solution to be adsorbed as a function of pH (T = 313 K, adsorption time = 25 min, C_GO = 100 mg L⁻¹, V_GO = 10 mL, C[Y(III)]_initial = 12 mg L⁻¹, V[Y(III)] = 25 mL). The vertical line indicates the onset pH of Y(III) precipitation from the C[Y(III)]_initial = 12 mg L⁻¹ solution. (b) Effect of pH of HNO₃ solution on the desorption of Y(III) on GO nanosheets in colloidal suspensions (pH = 0.9, V_HNO3 = 25 mL, desorption time: 60 min). The inset is a photo of GO suspensions after desorption in nitric acid solutions with different pH.

Fig. 2b shows the effect of pH of nitric acid solution on the desorption behavior of Y(III) on GO nanosheets in colloidal suspensions and a photo of GO suspensions after desorption in nitric acid solutions with different pH. As the pH of nitric acid solution for desorption varies from 0.1 to 4.0, the desorption rate of Y(III) on GO nanosheets increases to start with and then decreases, achieving peak value of 93% at pH = 0.9, which does not coincide with the common belief that the more acidic the desorption solution is, the higher is the desorption. From the inset image of Fig. 2b, it can be seen that the pH value of nitric acid solution for desorption has a great influence on the dispersion state of GO suspension after desorption. More significantly, it can be found that the desorption rate has an obvious correlation with the agglomeration extent of regenerated GO suspension. As demonstrated in Fig. 2b, the GO after desorption almost resumes the initial colloid state and shows highest desorption rate at pH = 0.9. Moreover, the darker and more aggregated the GO suspension is after desorption, the lower is the corresponding desorption rate of Y(III) on GO nanosheets. When GO suspension is regenerated in the desorption solution at very low pH, the high concentration of H⁺ may result in the restacking and agglomeration of GO nanosheets, which will deter ion exchange between Y(III) and H⁺ to some extent and lead to a drop in Y(III) desorption rate. In summary, the pH value of the desorption solution is critical to high desorption rate of Y(III) on GO nanosheets.

The effects of ionic strength on adsorption and desorption of Y(III) on GO nanosheets in colloidal suspensions are presented in Fig. 3. The effect of ionic strength on desorption and adsorption of Y(III) on GO nanosheets demonstrates a similar evolution tendency. The variation of NaClO₄ concentration from 0 to 0.03 M leads to a moderate reduction of 6.91 mg g⁻¹ and 3.09% in adsorption capacity and desorption rate of Y(III) on GO nanosheets, respectively. And further increasing the NaClO₄ concentration from 0.03 M to 0.30 M results in a minor decrease of 1.97 mg g⁻¹ and 1.38% in adsorption capacity and desorption rate, respectively. This can be interpreted as follows: (1) as the adsorption interactions between the functional groups and Y(III) ions are mainly ionic ones, the introduction of NaClO₄ into the GO suspension reduces the available sites to bind Y(III) ions on GO surfaces as a result of competition with Na(I); and (2) when the available adsorption sites on GO surfaces are occupied by Na(I), the further enhancement of NaClO₄ concentration boosts the activity coefficient of Y(III) and restricts Y(III) transfer from solution to solid surface to a minor extent.¹⁷

Fig. 3 Effect of ionic strength (C_NaClO4) on adsorption–desorption of Y(III) on GO nanosheets in colloidal suspensions. (Using NaClO₄ as added electrolyte, T = 303 K, adsorption time: 25 min; using pH = 0.9 HNO₃ as desorbent, desorption time: 60 min.)

The effects of temperature on adsorption and desorption of Y(III) on GO nanosheets in colloidal suspensions are shown in Fig. 4a and b, respectively. As the temperature increases from 303 K to 343 K, the time for Y(III) to reach adsorption equilibrium on GO nanosheets drastically drops from 20 min to 6 min while adsorption capacity only increases from 185.97 mg g⁻¹ to 194.01 mg g⁻¹, a minor increase of 4.32%. As for the desorption of Y(III) on GO nanosheets, as the temperature increases from 303 K to 333 K, the time for Y(III) to reach desorption equilibrium on GO nanosheets drastically drops from 60 min to 20 min while the desorption rate climbs up slowly from 90.63% to 94.36%, a rise of 3.73%. It is noticeable that on further increasing the temperature to 343 K, the time for Y(III) to reach desorption equilibrium remains unchanged while the desorption rate falls to 78.93%, which can be owing to the observed aggregation and sedimentation of GO at over 343 K. It is understandable that increasing temperature speeds Y(III) transfer from solution to the surface of GO or the opposite.

Fig. 4 Effect of temperature on adsorption (a) and desorption (b) of Y(III) on GO nanosheets (adsorption time: 25 min; desorption time: 60 min).

3.3 Adsorption isotherm and thermodynamics

Adsorption isotherms of Y(III) on GO nanosheets at three different temperatures are shown in Fig. 5. Adsorption isotherms can be generated based on numerous theoretical models; the Langmuir and Freundlich models are the most frequently used. In order to explore the adsorption mechanism, as shown in Fig. 5, the adsorption isotherms of Y(III) on GO were simulated with the Langmuir (C_e/q_e = C_e/q_max + 1/q_maxK_L) and Freundlich (q_e = K_FC_e^1/n) models, where C_e is the equilibrium concentration of Y(III) in aqueous solution (mg L⁻¹), q_e is the amount of Y(III) adsorbed on colloidal GO (mg g⁻¹), q_max is the maximum amount of Y(III) adsorbed per unit weight of GO to form a complete monolayer coverage on the surface, K_L is the Langmuir adsorption equilibrium constant, which represents enthalpy of adsorption and should vary with temperature, and K_F and n are the Freundlich constants related to the adsorption capacity and adsorption intensity, respectively. The values of q_max and K_L are calculated from the slope and intercept of a linear plot of C_e/q_e against C_e. ln K_F and 1/n can be obtained from the intercept and the slope of a linear plot of ln q_e versus ln C_e. The parameters calculated from Langmuir and Freundlich models are listed in Table 1.

Fig. 5 Adsorption isotherms of Y(III) on GO nanosheets at different temperatures. The solid lines represent adsorption model and the dashed lines Langmuir model simulations.

Table 1 Parameters for Langmuir and Freundlich models of Y(III) adsorption on GO

Experimental conditions	Langmuir			Freundlich
	qmax (mg g^−1)	KL (L mg^−1)	R^2	KF (mg^1−n L^n g^−1)	n	R^2
pH = 5.9 ± 0.1	190.48	2.59	0.9994	139.39	0.138	0.9904
T = 303 K

---

As shown in Fig. S1,† the Langmuir equation fits the experimental data better than the Freundlich model with a higher correlation coefficient (R²) of 0.9994, indicating that Y(III) is adsorbed by specific sites on the surface of colloidal GO sheet and forms an adsorption monolayer. The maximum adsorption capacity (q_max) of Y(III) on GO calculated from the Langmuir model is 190.48 mg g⁻¹ at pH = 5.9 ± 0.1. Compared with q_max values of Y(III) adsorption on other adsorbents (Table 2), such as by-pass cement,⁴ bacterial cell walls,¹¹ and polyethyleneglycol (phosphomolybdate and tungstate) heteropolyacid sorbents,¹² GO has the highest adsorption capacity among the reported adsorbents for Y(III) so far. This can be explained as follows: (1) the wider c-axis spacing of GO nanosheets enables Y(III) ions to enter easily into the interlayer space of GO nanosheets and effectively bind with the abundant oxygen-containing functional groups on the surface of GO;³³ and (2) serving as Lewis base, the delocalized π-electron systems can form electron donor–acceptor complexes with Y(III) ions acting as Lewis acid.^17,35

Table 2 Comparison of maximum adsorption capacity of Y(III) on different adsorbents

Adsorbents	Experimental conditions	Adsorption capacity (mg g^−1)	Ref.
By-pass cement dust	T = 298K, pH = 7.0, C = 200 mg L^−1	4	4
Sulfate-reducing bacteria	T = 297K, pH = 4.5, C = 0.1 mg L^−1	0.00434	11
Phototrophic bacteria	T = 297K, pH = 4.5, C = 0.1 mg L^−1	0.0026	11
H, PEG, PW	T = 298K, CHCl = 0.2 M, C = 400 mg L^−1	55	12
H, PEG, PMo	T = 298K, CHCl = 0.2 M, C = 400 mg L^−1	66	12
Colloidal GO	T = 303K, pH = 5.9 ± 0.1, C = 12 mg L^−1	190.48	This study

---

The thermodynamic parameters (ΔH⁰, ΔS⁰ and ΔG⁰) for Y(III) adsorption on GO nanosheets can be calculated from the temperature-dependent adsorption isotherms. The standard free energy change (ΔG⁰) can be calculated from the following equation: ΔG⁰ = −RT ln K⁰, where R is the universal gas constant (8.314 J mol⁻¹ K⁻¹); T is the temperature of aqueous solution in kelvin; and the adsorption equilibrium constant, K⁰, can be calculated by plotting ln K_d versus C_e (Fig. S2†) and linearly extrapolating C_e to zero. The standard enthalpy change (ΔH⁰) and the standard entropy change (ΔS⁰) are calculated according to the following equation: ln K⁰ = ΔS⁰/R − ΔH⁰/RT. The slope and intercept of a plot of ln K⁰ versus 1/T are −ΔH⁰/R and ΔS⁰/R, respectively (Fig. S3†).

The thermodynamic parameters calculated from adsorption isotherms at 303 K, 323 K and 343 K are listed in Table 3. The value of ΔH⁰ is positive, indicating that Y(III) adsorption on GO is an endothermic adsorption process. This phenomenon can be explained as follows: as Y(III) ions are well solvated in aqueous solution, hydrated Y(III) ions must have their hydration sheath denuded to some extent prior to being adsorbed on GO, which is an energy-absorbing process. Based on a previous study,³⁵ the energy of dehydration exceeds the exothermicity of cations to be attached to GO nanosheets. It can be concluded that the dehydration of Y(III) ions is a dominant endothermic process. The negative values of ΔG⁰ suggest Y(III) adsorption on GO is a spontaneous process. The increase in negative values of ΔG⁰ with increasing temperature indicates that a higher temperature would be more favorable for adsorption of Y(III) on GO. With increasing temperature, the hydrated Y(III) ions tend to dehydrate more easily and thus Y(III) ion adsorption on GO proceeds more easily. The positive value of ΔS⁰ suggests the affinity of GO toward Y(III) in aqueous solutions and the enhanced randomness for Y(III) ion adsorption onto the active sites of GO during adsorption.

Table 3 The thermodynamic parameters for Y(III) adsorption on GO nanosheets

ΔG^0 (kJ mol^−1)			ΔH^0 (kJ mol^−1)	ΔS^0 (J mol^−1 K^−1)
303 K	323 K	343 K
−37.20	−40.35	−43.82	12.93	165.37

---

3.4 Kinetics and modeling

The contact time between the metal ions and the adsorbent is regarded as a crucial issue in high-efficiency recovery of metal ions from the wastewater via adsorption. Hence, in the present study, the kinetics of Y(III) removal by adsorption of the colloidal GO suspensions was investigated to understand the adsorption behavior of the colloidal GO suspensions.

In order to elucidate the kinetics of the adsorption process, two conventional pseudo-first-order and pseudo-second-order kinetic models^36,37 have been employed to fit the experimental adsorption data in this work, which can be expressed by their nonlinear forms as follows:

pseudo-first-order model:

ln(q_e − q_t) = ln q_e − k₁t

pseudo-second-order model:

where k₁ (min⁻¹) and k₂ (mg g⁻¹ min⁻¹) are the adsorption rate constants of the pseudo-first-order model and pseudo-second-order model, respectively; q_e is the actual equilibrium adsorption capacity of adsorbent (mg g⁻¹); and q_t is the actual adsorption capacity of adsorbent after contacting for t minutes (mg g⁻¹).

The plots of pseudo-first-order and pseudo-second-order kinetic models for Y(III) adsorption on GO nanosheets are presented in Fig. 6a, and the parameters for the two kinetic models are summarized in Table S1.† Fig. 6a shows that the adsorption kinetics can be perfectly fitted by the pseudo-second-order model with correlation coefficient R² = 0.9982, suggesting that the adsorption process follows a pseudo-second-order model.

Fig. 6 (a) Kinetic models of pseudo-first-order and pseudo-second-order. (b) Intraparticle diffusion kinetics for Y(III) adsorption on GO nanosheets.

In general, the adsorption process consists of three consecutive steps, namely (a) external diffusion (surface adsorption); (b) intraparticle diffusion (pore diffusion); and (c) the final adsorption equilibrium on active sites.³⁸ The final step is very fast relative to the other two. Therefore, the sorption of adsorbate on sorbent may be governed by film diffusion process and/or intraparticle diffusion. To elucidate the diffusion mechanism and determine the actual rate-controlling step, regression analysis was carried out for a plot of Y(III) adsorbed amount (q_t) versus the square root of time (t^0.5) according to the Weber–Morris intraparticle diffusion model, q_t = k_pt^0.5 + C,³⁹ where k_p is the intraparticle diffusion constant (mg g⁻¹ min^−0.5) and C gives an idea about the thickness of the boundary layer. Based on the model, if the plot passes through the origin (C = 0), it indicates that the intraparticle diffusion is the only rate-controlling step; if the plot does not pass through the origin (C≠0), this suggests that the intraparticle diffusion is not the only rate-controlling step, but also other kinetic processes may control the adsorption rate simultaneously. As shown in Fig. 6b, the plot of q_t versus t^1/2 has three distinct regions, suggesting that more than one process dominates the adsorption. The first higher gradient region represents external diffusion and covers most of the adsorption period, which might be because confinement of GO in a dialysis bag increases ion diffusion distance and enhances ion diffusion hindrance. The second region is the gradual adsorption stage, which corresponds to intraparticle diffusion. The third region suggests adsorption–desorption equilibrium. Apparently, the plot does not pass through the origin, indicating that the intraparticle diffusion is not the only rate-controlling step for the adsorption process. Similar adsorption behavior was observed by Ren et al.⁴⁰ in the adsorption of copper and lead ions onto graphene nanosheet/δ-MnO₂.

3.5 Recycling and regeneration of colloidal graphene oxide suspensions

It is well-known to us that an ideal adsorbent should not only possess high adsorption–desorption capability, but also have excellent reusability from the viewpoint of economy and applicability. Considering that the regeneration ability of GO is highly crucial to its practical application, experiments of consecutive adsorption–desorption cycles were conducted by using GO suspension loaded in a dialysis bag as adsorbent and pH = 0.90 HNO₃ aqueous solution as desorption agent to investigate the desorption and adsorption behaviors of GO.

From Fig. 7, it can be seen that the desorption rate in the fourth adsorption–desorption cycle still remains at 74.26%, suggesting that most Y(III) adsorbed on the surface of the GO could be desorbed using pH = 0.90 HNO₃ aqueous solution. More significantly, Fig. 7 indicates that GO still preserves an adsorption capacity of 138.73 mg g⁻¹, a reduction of 22.92%, after three consecutive adsorption–desorption cycles. The decreasing adsorption capacity of GO after several adsorption–desorption cycles suggests that a fraction of the sites are irreversibly bound by Y(III). The reason may be that with increasing adsorption–desorption cycles, the restacking of GO nanosheets intensifies, which makes Y(III) ion desorption more difficult and exposes fewer active sites available for adsorption. As to the inset in Fig. 2b, the precipitated GO nanosheet suspension after adsorption saturation can resume a colloidal state when using pH = 0.90 HNO₃ aqueous solution as desorption agent. Therefore, the high adsorption capacity and desorption rate of the colloidal GO indicate the regenerability and reusability of GO and promises a good prospect for application of GO in practical wastewater treatment.

Fig. 7 Histograms for the adsorption capacity (q_e) and desorption rate (R_d) of Y(III) on colloidal GO suspensions in consecutive adsorption–desorption cycles.

4. Conclusions

Herein, a novel and re-pollution-free route for highly efficient recovery of trace Y(III) from wastewater by adsorption of aqueous colloidal suspension of GO loaded in a dialysis bag has been proposed. At pH = 5.9 ± 0.1 and T = 303 K, the adsorption capacity of Y(III) on colloidal GO nanosheets can amount to 190.48 mg g⁻¹ after 25 min adsorption, higher than any other adsorbents reported so far. The Y(III)-saturated GO suspension can be easily desorbed and resume a colloidal state in pH = 0.90 HNO₃ solution with desorption rate of 74.26% in the fourth adsorption–desorption cycle. In summary, GO nanosheets may act as a highly efficient and easily regenerable adsorbent in enrichment and recovery of trace Y(III) from wastewater. More significantly, the innovative combination of colloidal GO suspension with dialysis membrane offers a facile and feasible strategy for re-pollution-free adsorptive separation and recovery of other metal ions from wastewater.

Acknowledgements

We are grateful for financial support from the Project in the National Science & Technology Pillar Program of China (2012BAE01B02), National Natural Science Foundation of China (no. 51464033 and no. 21061011) and Jiangxi Provincial Scientific & Technological Support Project of China (no. 20132BBE500041).

References

1. R. Chi and J. Tian, Weathered crust elution-deposited rare earth ores, Nova Science Publishers, New York, 2008.
2. S. L. Tong, W. Z. Zhu, Z. H. Gao, Y. X. Meng, R. L. Peng and G. C. Lu, J. Environ. Sci. Health, Part A: Toxic/Hazard. Subst. Environ. Eng., 2004, 39, 2517–2532.
3. C. R. Li, Z. Y. Zhuang, F. Z. Huang, C. Wu, Y. P. Hong and Z. Lin, ACS Appl. Mater. Interfaces, 2013, 5, 9719–9725.
4. H. H. Osman, S. A. Sayed and M. E. H. Shalabi, J. Hazard. Mater., 2011, 195, 62–67.
5. M. R. Yaftian, M. Burgard, C. B. Dieleman and D. Matt, J. Membr. Sci., 1998, 144, 57–64.
6. R. Chi, Y. Hu, G. Zhu, S. Xu, Z. Zhou and Z. Xu, Metall. Mater. Trans. B, 2003, 34, 611–617.
7. S. P. Dubey, K. Gopal and J. L. Bersillon, J. Environ. Biol., 2009, 30, 327–332.
8. K. C. Kemp, H. Seema, M. Saleh, N. Le, K. Mahesh, V. Chandra and K. Kim, Nanoscale, 2013, 5, 3149–3171.
9. H. M. H. Gad and N. S. Awwad, Sep. Sci. Technol., 2007, 42, 3657–3680.
10. Y. Takahiro, O. Takuo, O. Toshihiko and J. F. Arokiasamy, Chem. Geol., 2004, 21, 239–246.
11. Y. Takahashi, X. Châtellier, K. H. Hattori, K. Kato and D. Fortin, Chem. Geol., 2005, 219, 53–67.
12. L. Zhang, S. D. Ding, T. Yang and G. C. Zheng, Hydrometallurgy, 2009, 99, 109–114.
13. S. B. Wang, H. Q. Sun, H. M. Ang and M. O. Tadé, Chem. Eng. J., 2013, 226, 336–347.
14. R. D. Daniel, P. Sungjin, W. B. Christopher and S. R. Rodney, Chem. Soc. Rev., 2010, 39, 228–240.
15. D. Li, M. Marcb, E. Scottgilj, K. Richardb and G. W. Gordon, Nat. Nanotechnol., 2008, 3, 101–105.
16. R. Sitko, E. Turek, B. Zawisza, E. Malicka, E. Talik, J. Heimann, A. Gagor, B. Feist and R. Wrzalik, Dalton Trans., 2013, 42, 5682–5689.
17. G. X. Zhao, J. X. Li, X. M. Ren, C. I. Chen and X. K. Wang, Environ. Sci. Technol., 2011, 45, 10454–10462.
18. G. X. Zhao, X. M. Ren, X. Gao, X. L. Tan, J. X. Li, C. I. Chen, Y. Y. Huang and X. K. Wang, Dalton Trans., 2011, 40, 10945–10952.
19. G. X. Zhao, T. Wen, X. Yang, S. B. Yang, J. L. Liao, J. Hu, D. D. Shao and X. K. Wang, Dalton Trans., 2012, 41, 6182–6188.
20. Y. B. Sun, Q. Wang, C. I. Chen, X. L. Tan and X. K. Wang, Environ. Sci. Technol., 2012, 46, 6020–6027.
21. Z. Q. Bai, Z. J. Li, C. Z. Wang, L. Y. Yuan, Z. R. Liu, J. Zhang, L. R. Zheng, Y. L.Zhao, Z. F. Chai and W. Q. Shi, RSC Adv., 2014, 4, 3340–3347.
22. J. Yang, J. X. Wu, Q. F. Lü and T. T. Lin, ACS Sustainable Chem. Eng., 2014, 2, 1203–1211.
23. Y. B. Sun, D. D. Shao, C. L. Chen, S. B. Yang and X. K. Wang, Environ. Sci. Technol., 2013, 47, 9904–9910.
24. X. L. Wu, L. Wang, C. L. Chen, A. W. Xu and X. K. Wang, J. Mater. Chem., 2011, 21, 17353–17359.
25. V. Chandra, J. Park, Y. Chun, J. W. Lee, I. C. Hwang and K. S. Kim, ACS Nano., 2010, 4, 3979–3986.
26. J. H. Zhu, S. Y. Wei, H. B. Gu, S. B. Rapole, Q. Wang, Z. P. Luo, N. Haldolaarachchige, D. P. Young and Z. H. Guo, Environ. Sci. Technol., 2012, 46, 977–985.
27. L. L. Fan, C. N. Luo, M. Sun and H. M. Qiu, J. Mater. Chem., 2012, 22, 1039–1046.
28. H. M. Sun, L. Y. Cao and L. H. Lu, Nano. Res., 2011, 4, 550–562.
29. J. Li, S. W. Zhang, C. L. Chen, G. X. Zhao, X. Yang, J. X. Li and X. K. Wang, ACS Appl. Mater. Interfaces, 2012, 4, 4991–5000.
30. L. Zhang, X. Li, Y. Huang, Y. F. Ma, X. J. Wan and Y. S. Chen, Carbon, 2010, 48, 2367–2371.
31. C. M. Chen, Q. H. Yang, Y. G. Yang, W. Lv, Y. F. Wen, P. X. Hou, M. Z. Wang and H. M. Cheng, Adv. Mater., 2009, 21, 3007–3011.
32. D. C. Marcano, D. V. Kosynkin, J. M. Berlin, A. Sinitskii, Z. Z. Sun, A. Slesarev, L. B. Alemany, W. Lu and J. M. Tour, ACS Nano, 2010, 4, 4806–4814.
33. M. J. McAllister, J. L. Li, D. H. Adamson, H. C. Schniepp, A. A. Abdala, J. M. Liu, M. Herrera-Alonso, D. L. Milius, R. Car, R. K. Prud'homme and I. A. Aksay, Chem. Mater., 2007, 19, 4396–4404.
34. K. N. Kudin, B. Ozbas, H. C. Schniepp, R. K. Prud'homme, I. A. Aksay and R. Car, Nano Lett., 2008, 8, 36–41.
35. C. Laurence and J. F. Gal, Lewis Basicity and Affinity Scales: Data and Measurement, Wiley, New York, 2009.
36. C. W. Hoogendam, A. De Keizer, M. A. Cohen Stuart and B. H. Bijsterbosch, Langmuir, 1998, 14, 3825–3839.
37. Y. Liu and L. Shen, Langmuir, 2008, 24, 11625–11630.
38. N. Li, Z. Mei and X. Y. Wei, Chem. Eng. J., 2012, 192, 138–145.
39. W. J. Weber and J. C. Morris, J. San. Eng. Div., 1963, 89, 31–59.
40. Y. M. Ren, N. Yan, J. Feng, J. Ma, Q. Wen, N. Li and Q. Dong, Mater. Chem. Phys., 2012, 136, 538–544.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra09175b

---