Chemical computing based on Turing patterns in two coupled cells with equal transport coefficients

Abstract

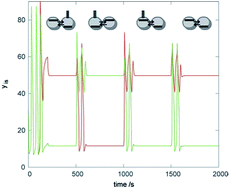
We study instabilities leading to inhomogeneous stationary states (discrete Turing patterns) using a simple model of glycolytic oscillatory reaction in two mass-coupled stirred open reactors with equal coupling coefficients of the activator and inhibitor and explore their ability to serve as logical devices. The system represents the simplest coupled cell system. It is found to possess coexisting stable homogeneous oscillations and a pair of stable complementary asymmetric Turing patterns. We examine transitions from the oscillatory regime to Turing patterns, or from one pattern to another, elicited by targeted perturbations specific for each type of transition. We further develop our earlier proposition of using the Turing patterns in chemical computing and explore logical functions available in the two cell system. Digital memory storage, a sensor, a signal conducting module and simple logic gates using NAND, AND, OR, NOR, and NOT functions are found. The main advantage of the two-cell system is that it can serve as a basic unit in the construction of a lattice representing a universal chemical processor, whereas larger linear or circular arrays are more suitable for tailor-made operations.

---

I. Introduction

In an array of coupled cells with diffusive transport of species spatiotemporal patterns may occur due to interaction of transport with reaction possessing positive and negative feedback.^1,2 Turing described four types of spatiotemporal patterns that he proposed to serve as a chemical basis of morphogenesis.³ The case when spatial distribution is inhomogeneous and stationary is called a Turing pattern. Even though involvement of Turing patterns in biological morphogenesis is a matter of controversy, there is growing body of experimental work, which supports a Turing pattern triggered genetic program for cell differentiation.^4,5 The ligand–receptor model of development of mice limbs shows importance of concentration field of key species based of a Turing mechanism for occurrence of proper growth otherwise excessive or insufficient number of digits would occur.⁶ Necessary conditions for emergence of a spontaneous Turing pattern are open system and differential transport for activatory and inhibitory species^7,8 – a situation frequently termed short range activation and long-range inhibition. Diffusion usually makes the system uniform, but at a time scale comparable to that for the reaction it becomes a key element of nonuniformity. Turing patterns occurring in a tissue can be modeled in a continuous spatial domain, or the tissue can be resolved into population of discrete cells treated as open stirred chemical reactors if the purpose is to study smaller multicellular systems or artificial cell structures. The number of cells in the tissue affects the form of Turing pattern (dots, stripes, labyrinth, hexagons, or their combination), which can be a key element for stabilization of pattern selection.^9–11

Spontaneous occurrence of Turing pattern has been demonstrated experimentally on several chemical systems, notably on chlorite–iodide–malonic acid (CIMA) system in a thin layer of gel.^12–17 The activator (iodide ions) has a lowered diffusivity due to addition of starch in the solution, thus creating long-range inhibition leading to a hexagonal pattern. Diffusivity of iodide ions can be also decreased by introducing micelles,¹⁸ thus creating hexagonal and labyrinth like patterns with characteristic size about 10 μm. Other chemical systems displaying Turing patterns include the Belousov–Zhabotinsky (BZ) reaction in reverse micelles,¹⁹ the system with pH-sensitive thiourea–iodate–sulfite reaction²⁰ in gel and the chlorine dioxide–iodine–malonic acid (CDIMA).^17,21 In addition to spatially continuous systems, the spatially discrete system allowing the BZ reaction to proceed in tightly packed droplets arranged in 1D or 2D arrays also display Turing patterns.^22,23

Remarkably, Turing patterns can occur even with equal diffusivities (or transport coefficients in the coupled cell systems).^24,25 In this case Turing patterns do not occur spontaneously, yet they exist and can be reached by targeted perturbations. Typically, the stationary pattern coexists with stable oscillations and switching the dynamics from oscillations to the Turing pattern is known as oscillation death.^4,26,27 Our primary interest is studying transitions from oscillations to Turing pattern and back by using targeted perturbations. Controlled transitions may serve various purposes. For example, regulation of positive and negative feedback with time delay leads to transitions between antispirals, maze and hexagon type of Turing patterns.¹¹ They can also be used for collective decision making of cell arrays or assemblages. Alternatively, decision making can be realised by controlling outputs of a cascade of enzymes that can amplify the signal, operate as a logic gate or work as neural network when coupled with other cascades.^28,29

Experimental coupled cell systems^26,27,30,31 frequently use non-selective coupling, such condition may occur in nature as well, for example, DNA coupling during chromosomal replication,³² temperature and domain size during cellular division,³³ calcium coupling in cell division³⁴ and potassium coupling in neural networks.³⁵ Because of its biological relevance and also because of potential amenability to experimenting the system chosen for analysis is glycolysis in two coupled reactors with equal coupling coefficients. We have shown earlier that in the linear three-array with glycolytic reaction the available coexisting inhomogeneous patterns can be conveniently used as logical devices with multiple functions enabling collective decision making.²⁵ Here we show that despite its simplicity even the two-cell system allows for construction of simple logical gates. A core model of glycolysis due to Moran and Goldbeter³⁶ is used in modelling. The main tool for our analysis is numerical continuation^37,38 which involves two-parameter bifurcation diagrams used to find ranges of parameters favorable for occurrence of Turing patterns, one-parameter bifurcation diagrams (or solution diagrams)³⁷ to identify details of bifurcations leading to stabilization of Turing patterns and to provide information on concentration levels of reacting species. Perturbations that lead to pattern switching were searched for by using direct numerical integration. Because of coexistence of Turing patterns with homogeneous oscillations, all logic gates require special preconditioning perturbations to suppress homogeneous oscillations.

In Section II we introduce a model of two coupled cells with glycolytic reaction and in Section III we analyze space of relevant parameters to find proper conditions for stationary stable Turing patterns. In Section IV we use perturbations to obtain desired dynamical behavior and interpret the result in terms of various logical devices. We also propose construction of such devices. In Section V we discuss the chemical computing techniques obtained with two coupled cells and compare them with other proposed strategies.

II. Formulation of the model

Two coupled cells

We consider two cells coupled by diffusive transport. The cells are modelled as open stirred reactors operating at identical conditions. The evolution equations are based on the mass balances for n species in each cell:where X_i is n-vector of concentrations in cell i and the rate n-vector F(X_i) includes input/output and chemical production/consumption of each species in cell i. Transport coefficients for all species are arranged in the vector K = (k₁, … , k_n). A special case of interest occurs when the transport coefficients are all equal, k = k₁ = k₂ = … = k_n. The homogeneous stationary state satisfies

X̄ = X₁ = X₂ and f(X̄) = 0. (2)

Turing³ found that variation of coupling strength in discrete systems such as eqn (1) as well as in spatially continuous reaction-diffusion systems may lead to spontaneous emergence of an inhomogeneous stationary state – the Turing pattern provided that transport/diffusion coefficients are unequal and the homogeneous stationary state is unique. For eqn (1), this instability occurs when the Jacobi matrix J of eqn (1) at X̄ has a real eigenvalue which becomes unstable upon variation of K, while other eigenvalues remain stable. Consequently, the homogeneous stationary state becomes unstable via a primary symmetry breaking bifurcation and a stable inhomogeneous stationary state occurs past the bifurcation point. Turing discovered that this phenomenon requires the transport coefficient of an activator to be less than that of an inhibitor. This observation is commonly phrased as short range activation and long range inhibition because the activator is entrapped in one place due to slow diffusion, while the inhibitor can diffuse over significantly larger distances.

The situation is more subtle when equal transport coefficients are considered.⁸ Eigenvalues λ of J are the roots of³⁹

In the case of equal transport coefficients, diag(K) = kE. It has been shown in ref. 8 that variation of k makes the eigenvalues calculated from eqn (3a) unstable in the presence of already unstable eigenvalues determined by eqn (3b). Therefore the homogeneous stationary state is already unstable, when the symmetry breaking bifurcation occurs. Consequently, the inhomogeneous stationary state is also unstable and, given the uniqueness of the homogeneous stationary state, stable homogenous oscillations bifurcating via a pair of pure imaginary eigenvalues associated with eqn (3b) are observed. However, the unstable Turing stationary state can be stabilised due to further variation of k via a secondary bifurcation.^8,26,40 Thus stable oscillations and stable Turing pattern can coexist within a range of coupling strength k. In this paper we focus on perturbations capable of inducing transitions between these modes.

Kinetics of glycolysis

The kinetic model used here is a two-variable core model of glycolysis proposed by Moran and Goldbeter.³⁶ The model possesses activation (positive feedback) mediated by a cooperative enzyme phosphofructokinase (PFK) and inhibition (negative feedback) mediated by enzyme(s) from lower part of the glycolytic reaction chain. The variables are concentrations of adenosine triphosphate (ATP) – the inhibitor x, and adenosine diphosphate (ADP) – the activator y. Eqn (1) with incorporated core glycolytic kinetics take the form:where the kinetic terms are

In eqn (4b) ν is the ATP uptake rate, σ_M is the rate coefficient of the autocatalytic step, L is the corresponding allosteric constant, σ_I is the rate coefficient of the recycling inhibitory reaction, n is the corresponding Hill coefficient and M is the corresponding Michaelis constant, k_S is the rate coefficient of ADP degradation, p is a stoichiometric factor. All parameters and variables except for time are dimensionless.³⁶ The parameters σ_M, σ_I are taken as adjustable to be used in constructing bifurcation diagrams, the value of ν = 1.84 s⁻¹ is chosen so that the system has a unique homogeneous stationary state. Other parameters are taken from ref. 36: L = 5 × 10⁶, n = 4, M = 10, k_S = 0.06 s⁻¹, p = 1.

Relation to a more comprehensive model of glycolysis⁴¹ is indicated in Fig. 1. The PFK mediated phosphorylation of fructose-6-phosphate is consuming ATP and producing ADP. The resulting ADP activates PFK (back double activation⁴²), which implies autocatalysis. The ATP also acts as an allosteric inhibitor. The inhibitory reaction that recycles ATP is mediated by pyruvate kinase and phosphoglycerate kinase. Negative feedback necessary for oscillatory dynamics is two-fold, one part is due to limited uptake rate of ATP, the other is implied by the recycling reaction. Positive feedback coupled with two-fold negative feedback provides for multistable stationary states, but also for multistable limit cycles (birhythmicity³⁶) in a single cell. Since we focus on emergent behavior in coupled cells, we choose parameters corresponding to a unique stationary state and limit cycle in a single cell.

Fig. 1 Simplified scheme of the glycolytic reaction chain. Reactions in circles are used in the core model.

Since both activator and inhibitor have essentially the same diffusivity, we assume equal transport rate coefficients. The relevant range of k can be roughly estimated as follows: k = (diffusion coefficient/membrane thickness) × (cell surface/cell volume). Entire surface of the cell would yield k = (300–6000) s⁻¹, when considering the value of the diffusion coefficient of ATP/ADP ∼10⁻⁶ cm² s⁻¹,⁴³ cell diameter (10–200) μm and membrane thickness ≈10 nm. Adjacent cells can diffusively exchange ATP/ADP by only a small fraction of their surface. In our calculations the instabilities leading to Turing stationary states occur for a range of k on the order of 10⁻¹ s⁻¹ thus we chose k = 0.1 s⁻¹ for detailed analysis. Glycolysis can be also performed in vitro, for example using yeast extract in a CSTR;⁴⁴ in such experiments k would be rather easily controlled either by the choice of a specific membrane or by using reciprocal pumping²⁶ between two CSTRs. Preliminary experiments in such an arrangements have already been initiated.⁴⁵ Below we will refer to coupled CSTRs experiments when discussing relevant ranges of parameter.

III. Occurrence of Turing stationary states – bifurcation analysis

Two-parameter analysis in σ_M–σ_I and σ_I–k planes

In general, the bifurcation diagram partitions a parameter space (typically of dimension two or three) into regions having distinct dynamics and separated from each other by boundaries corresponding to various kinds of bifurcations. The most relevant to the occurrence of Turing stationary states are the saddle-node (or fold) bifurcation, the Hopf bifurcation and the symmetry breaking bifurcation from stationary states. In a two-parameter space these codimension one bifurcations occur along curves delineating regions as shown in Fig. 2. In addition, the curves may intersect in codimension two bifurcation points. These diagrams can also be seen as representative cross-sections of the three-dimensional parameter space involving the rate coefficients of all three major processes: activation, inhibition and mutual transport. The original values of the kinetic parameters proposed in ref. 36 corresponding to characteristic conditions in the yeast are σ_M = 10 s⁻¹ and σ_I = (0–4) s⁻¹, here we explore a broader range 0–200 s⁻¹ for both σ_M, σ_I since these parameters may heavily depend on actual conditions.

Fig. 2 Bifurcation diagrams for eqn 4(a) and 4(b). (a) σ_M vs. σ_I, k = 0.1 s⁻¹; (b) σ_I vs. k, σ_M = 100 s⁻¹. Red curve – Hopf bifurcation, black curve – saddle-node bifurcation, blue curve – symmetry breaking bifurcation; full line delimits a stable regime, dashed lines indicate no change of stability when crossed transversally. TPI, TPII – mutually symmetric Turing patterns (stable inhomogeneous stationary states); SHSS – stable homogeneous stationary state; UHSS – unstable homogeneous stationary state; UISS – unstable inhomogeneous stationary state, SHO – stable homogeneous oscillations.

Fig. 2a is a cross-section through the (σ_M, σ_I, k) space for k = 0.1 s⁻¹. It shows two embedded regions delimited by curves of Hopf bifurcation. The larger one corresponds to stable homogeneous oscillations emerging from the stable homogeneous stationary state through a primary Hopf bifurcation. Enclosed within this region is the second region where the two mutually symmetric stable inhomogeneous stationary states coexist with stable homogeneous oscillations. This region is circumscribed by the curve of a secondary Hopf bifurcation, which stabilizes the inhomogeneous stationary state but does not give rise to stable oscillations. The unstable inhomogeneous stationary state is bifurcating from the unstable homogeneous stationary state along the curve of symmetry breaking bifurcation. The entire region of inhomogeneous stationary states including both stable and unstable ones is delimited in part by the curve of saddle-node bifurcation (black curve) and in part by the curve of symmetry breaking bifurcation (blue curve beyond the point of meeting with the black curve). In contrast to the Hopf bifurcation curves, crossing these bifurcation curves transversally does not lead to a change of stability. Other features (codimension two points, Hopf bifurcation curves that do not imply loss of stability of stationary states or emergence of stable oscillatory regimes) are subsidiary and hence omitted for clarity.

The pair of asymmetric stable Turing patterns is found in a diagonally extending region requiring σ_M > 41 s⁻¹ and σ_I > 23 s⁻¹. These values are higher than those mentioned above and used in modelling glycolytic oscillations. The elevated values may be obtained in a number of ways in experiments with the yeast extract: either by increasing temperature or the concentration of the extract, or by adding metabolites affecting the autocatalytic step, for example, fructose-2-6-bisphosphate,⁴⁶ which cancels out ATP inhibition, increases affinity for fructose-6-phosphate and increases thermal resistance of PFK.

Fig. 2b is another cross-section for fixed σ_M = 100 s⁻¹. In this rendering the Turing stationary states occur in a closed region and coexist there with stable homogeneous oscillations, which occupy a larger region delimited both from below and from above by two primary Hopf bifurcation curves.

One-parameter analysis for varying σ_I

The solution diagram is a plot of a norm of stationary states, periodic cycles, etc. against a chosen parameter (this is frequently and somewhat confusingly also called a bifurcation diagram in nonlinear physics and chemistry community). One-parameter branches of stationary states represented by the value y₁ = y_1SS together with branches of periodic cycles represented by minimum and maximum of y₁ are plotted against σ_I in Fig. 3 for fixed values of σ_M = 100 s⁻¹ and k = 0.1 s⁻¹. In addition, linearised stability of the solutions and local bifurcations are indicated. Because the inhibition reaction is strictly recycling and p = 1, the two reactions form a futile cycle. As a consequence, y at the homogeneous stationary state, y_1SS = y_2SS = ν/k_S does not depend on σ_I (nor on σ_M). As σ_I is increased, the diagram indicates a primary Hopf bifurcation yielding homogeneous oscillations, followed by the symmetry breaking bifurcation from the homogeneous stationary state giving rise to the pair of inhomogeneous stationary states that are mutually related by the cell-exchanging transformation (x_1SS, y_1SS, x_2SS, y_2SS) ↔ (x_2SS, y_2SS, x_1SS, y_1SS).These stationary states display the same stability and both become stable Turing patterns via a secondary Hopf bifurcation. Upon further increase the sequence of bifurcations is reversed. Namely, the Turing patterns become unstable through a secondary Hopf bifurcation, then merge and disappear via a symmetry breaking bifurcation and the homogeneous stationary state becomes stable along with simultaneous disappearance of homogeneous oscillations at another primary Hopf bifurcation. Other Hopf bifurcation points indicated in Fig. 3 are not associated with stable oscillations or stable stationary states. As a result, a pair of stable Turing patterns occurs within σ_I ≈ (31–70) s⁻¹ and coexists with stable homogeneous oscillations. The chemical computing techniques described below are built on the observation that targeted perturbations can induce transitions among the two stationary patterns and oscillations.

Fig. 3 Solution diagram plotting y₁ vs. σ_I for stationary states and homogeneous periodic oscillations. Red curve – stationary state, black curve – maxima and minima of homogeneous oscillations; full line – stable solution; dashed line – unstable solution; squares – Hopf bifurcation; diamonds – symmetry breaking bifurcation.

IV. Chemical computing devices

The bifurcation analysis in Section III shows in detail that stable homogeneous oscillations cover entire interval of σ_I, where Turing patterns may occur. Since the oscillations preclude spontaneous occurrence of Turing patterns, transitions from homogeneous oscillations to Turing stationary states need to be ensured by targeted perturbations. Such perturbations allow us to construct elementary chemical computing devices. In addition to σ_M = 100 s⁻¹ we chose σ_I = 35 s⁻¹ to maintain compatibility with anticipated yeast extract experiments (see Section III). There are two types of perturbations acting either to add or to remove selected species to/from a chosen cell. We call them positive/negative perturbations. Provided that we choose ATP as the perturbed species the dynamics is governed by:where p_i(t) is a sequence of perturbations in reactor i applied by imposing a constant inflow/outflow rate A_i, within a time ΔT. We call A_i the amplitude (positive or negative) of x, perturbations are applied at t_k. A sequence {t_k} of m perturbations (not necessarily periodic) is specifically chosen in each examined case to toggle between Turing patterns and oscillations. We set ΔT = 100 s, the amplitude of a positive perturbation A_i = 1.2 and that of a negative perturbation A_i = −0.5. Furthermore, we assume that the level of y (ADP) is monitored in each cell, which serves to evaluate the state of the system. The perturbation may be applied to one cell only or simultaneously to both cells, for the initial perturbation at t₁ = 100 s we always use A₁ = 1.2 and A₂ = −0.5 which leads to the {high, low} Turing pattern as described below.

Sensor and neural network module

Our calculations indicate that homogeneous oscillations cannot be switched to a Turing pattern by a perturbation applied to a single cell only. Instead, perturbation of both reactors simultaneously must be used. When the Turing pattern is established, the system can be switched to the other Turing pattern and back only by perturbation of one cell. Such transitions are achieved, when the positive perturbation with A_i = 1.2 is applied to the cell having a low stationary concentration of y. Clearly, autocatalysis is promoted by addition of ATP which eventually results in a switch to the complementary Turing pattern. If the positive perturbation with the same amplitude is applied to the cell with a high stationary concentration of y, the Turing pattern is disrupted only temporarily by an oscillatory transient and then the original stationary pattern reforms. The same result is obtained even when the perturbation time is doubled.

Let us denote the pattern {high, low} as TPI and the pattern {low, high} as TPII. The actual concentration profiles at the chosen parameter values are shown in Table 1.

Table 1 Dimensionless concentration profiles of inhomogeneous stationary states for TPI, TPII

	x1	x2	y1	y2
TPI	37.2	86.8	49.7	11.6
TPII	86.8	37.2	11.6	49.7

---

An example of transitions between TPI and TPII is shown in Fig. 4, indicating two effective switches followed by an ineffective one.

Fig. 4 Dynamic transitions between TPI and TPII for {t_k} = {100, 500, 1000, 1500} s. Red curve – first cell, green curve – second cell. Vertical bar indicates the cell to which the perturbation with A_i = 1.2 is applied.

We can use these observations to create a sensor that would detect an input signal (infusion of ATP) in the cell with low y by indicating a switch in the Turing pattern. Alternatively, the system may constitute an element of a neural network chain consisting of the two-cell modules that would mediate transfer of the input signal via sequence of pattern switches. Similar sensors or elements of neural network can operate in organisms.⁴⁷

Memory unit

Simultaneous perturbation of both cells can also lead to a transition between TPI and TPII. It is convenient to introduce the symbol 1 (logic 1) associated with A_i = 1.2 and the symbol 0 (logic 0) assigned to A_i = −0.5. Likewise, for the purpose of reading the output signal, a high concentration of y (40 < y < 79) in a Turing pattern is interpreted as output logic 1 and a low concentration of y (y < 15) as output logic 0. In order to reach one of the two complementary stationary patterns, complementary perturbations {1 0} or {0 1} are required. Thus the response dynamics of the system can be used as a memory array. The memory unit can be built in two ways: (a) a unit based on the one-cell perturbation as described in the sensor/neural network module (Fig. 4) or (b) a unit based on perturbing both cells shown in Fig. 5. The first method is simpler, due to usage of only one port for perturbation. However, sufficiently strong noise in the perturbation amplitude can break the Turing pattern and impose homogeneous oscillations. The second option requires two input ports for storing information in the form of a TP but the system is much more resistant to noise imposed homogeneous oscillations. In both cases, though, an exceedingly strong noise will result in a loss of memory due to oscillations. On the other hand, targeted strong perturbations may serve to erase the memory.

Fig. 5 Dynamic transitions between TPI and TPII for {t_k} = {100, 500, 1000, 1500} s. Red curve – first cell, green curve – second cell.

Logic gates

Turing patterns in two coupled cells can be also used for parallel chemical computing. In contrast to the inhomogeneous input signals {1 0} and {0 1}, the homogeneous input signals {1 1} and {0 0} lead to homogeneous oscillations. In order to have a complete logic gate, a knockout (control) perturbation needs to be introduced to restore a stationary pattern after the occurrence of homogeneous oscillations is indicated. The knockout perturbation should be applied automatically via a separate port combined with a reader indicating oscillations. In our simulations the knockout perturbation is triggered when the level of y if found to exceed 80. This level is well within the oscillatory amplitude but far above the high stationary level as seen in Fig. 3. Using the four types of input signals, we can construct a parallel logic gate performing two different logical functions. The homogeneous input signal induces homogeneous oscillations that are immediately overwritten by the knockout perturbation, which may be either {0 1} or {1 0}. The results shown in Fig. 6 can be used to deduce the corresponding logical truth tables. Table 2 summarizes input and output signals found in Fig. 6a. Based on these results, the two-array of cells works as two-input, two output logic gate calculating simultaneously two logical functions, ((NOT A₁)NOR A₂) and (A NAND(NOT A₂)). By using DeMorgan's theorem the functions can be also written as (A₁ AND(NOT A₂)) and ((NOT A₁)OR A₂), which shows that the two logical functions are mutually inverse. An important aspect of these logic functions is the NAND operation, which is conveniently used for more complex logical constructions. Therefore using a number of Turing pattern based gates, we can construct any logical function and therefore create a processor using a system of modules made up by two coupled reaction cells. In a similar fashion, from the dynamics in Fig. 6b the truth table in Table 3 is constructed.

Fig. 6 Dynamic responses for all four types of input signals with additional use of knockout perturbation. Red curve – first cell, green curve – second cell; (a) knockout perturbation {0 1}; (b) knockout perturbation {1 0}.

Table 2 Truth table using the knockout perturbation {0 1}

Input signals		Output signals
1st (A1)	2nd (A2)	1st cell (y1)	2nd cell (y2)
1	1	0	1
1	0	1	0
0	1	0	1
0	0	0	1
Resulting function		((NOT A1)NOR A2)	(A1 NAND(NOT A2))

---

Table 3 Truth table using the knockout perturbation {1 0}

Input signals		Output signals
1st (A1)	2nd (A2)	1st cell (y1)	2nd cell (y2)
1	1	1	0
1	0	1	0
0	1	0	1
0	0	1	0
Resulting function		((NOT A1)NAND A2)	(A1 NOR(NOT A2))

---

Implementation of a chemical logic gate

Since the outlined technique seems suitable for chemical computing, we make a further step toward a design of a chemical logic gate based on the glycolytic oscillatory reaction, e.g. using the yeast extract. The concept follows our earlier proposal²⁵ and is sketched in Fig. 7. It consists of two cells coupled by a membrane permeable for medium sized molecules such as ATP and ADP. Every cell has two input perturbation valves and an output reading sensor (e.g., optical), which discerns {high, low} and {low, high} Turing patterns as well as oscillations. Perturbation valves are means of delivering ATP or glycolytic enzymes (e.g., yeast extract) for positive perturbation and an ATP scavenger such as the enzyme apyrase can be used for a selective negative perturbation. Alternatively, adding water implies a simultaneous negative perturbation for all species, which we verified to be equally effective in the glycolytic model. Both cells have inputs for feeding yeast extract and glucose. A logic gate would require a knockout perturbation system.

Fig. 7 Schematic design of a device working as chemical logic gate using two coupled reaction cells. Red cylinder – inlet for yeast extract and glucose, orange cylinder – product outlet, green cylinder – inlet for perturbing the system with ATP, blue cylinder – inlet for perturbing the system with an ATP scavenger or water, yellow cylinder – inlet for knockout perturbations, black square window – optical sensor detecting concentration of ADP/ATP.

An alternative design more suited for a device on a microscale may be based on receptors, ports and special membranes mimicking devices used by living cells. All receptors need to be capable of reading ADP concentration (or any other suitable metabolite) and driving release of ATP for a defined amount of time. Ports transporting ATP are already available, for example, an artificial self-assembled hybrid membrane containing macrocyclic receptors that concurrently transport Na⁺ ions with ATP⁴⁸ could be used for ATP input. In addition, purinergic receptors⁴⁹ are known to initiate extracellular release of ATP through pannexin 1 channels,⁵⁰ which can be used as ATP output. An ultimate solution for microdevices used for memory storage and chemical computing based on Turing patterns would be based on artificial genome synthesis,^51,52 where types of receptors, ports, membranes and cell–cell junctions would be possible to design.

V. Discussion and conclusions

We analyzed simplest conceptual device for chemical computing based on two mass-coupled reactors with equal coupling coefficients for all species and a skeleton model of glycolysis. We found a region in the parameter space, where the stationary stable inhomogeneous state (Turing pattern) coexists with a homogeneous oscillatory regime. Such a situation is favorable for constructing various logical devices. We show that the array of two reaction cells provides simple binary and unary functions. Apart from direct use as a sensor or memory storage, the simplicity of the system makes it a convenient building block that may be used to construct a spatially distributed lattice functioning as a universal processor unit. In contrast, larger linear arrays used in our earlier work²⁵ perform complex simultaneous functions more suitable for single purpose operations. Also, we have aimed to set the parameters to correspond to conditions available in in vitro experiments with yeast extracts and conclude that experiments displaying the predicted patterns should be feasible.⁴⁵

We developed techniques capable of sensing, signal transduction, memory storage and signal processing based on two-valued logic. A system of concurrent memory devices would act as a digital memory storage bank as opposed to an analogue pattern storage technique based on the Hebbian learning rule developed by Hjelmfelt and Ross.^53–55 They developed a system based on a block of coupled bistable reactors, which works as a chemical alternative of a Hopfield network.⁵⁶ Bistability acts as substitution for excited and non-excited states, mass transport acts as connections through dendrites and axons. Mass transport has to be switched on and off to achieve proper functionality of this technique. The basic function of this “chemical” Hopfield network is pattern recognition within hours and it is robust against random noise.

The logic gate technique, which uses a specific glycolytic metabolic pathway occurring in a spatially homogeneous system (i.e., an open stirred reactor) was also developed by Hjelmfelt and Ross.⁵⁷ In connection with an invertor NOT, it works as a fuzzy NAND gate, which can be subsequently used to create any logic gate desired. In comparison, our technique requires at least two coupled reactors and performs only two-valued logic calculations. On the other hand, rather than employing specific pathways, the glycolysis as a whole is used. Moreover, glycolysis can be substituted by essentially arbitrary oscillatory reaction. Our technique demands more physical space, but in constructing a more complex systems such as a processor, we can assume microreactor arrays and parallelism to substitute for unavailable types of logic gates and thus overcome direct use of NAND gates.⁵⁷

Another type of systems capable of chemical computing is based on chemical waves in excitable or oscillatory regime within a microfluidic system containing lipid-encapsulated vesicles with the Belousov–Zhabotinsky (BZ) medium.⁵⁸ In particular, logic computing, signal transduction and diode functions were studied in a system analogous to the BZ-vesicles consisting of interconnected arrangements of gel disk subunits loaded with a photosensitive Belousov–Zhabotinsky medium.^59,60 The disk array is created by illuminating the gel layer with a computer generated pattern. The size of the disk influences its functionality and transduction. By coupling disks of varying size into an array with certain geometry, diode and various logical gates are obtained, for example, by using frequency coded variables.⁵⁹ Apart from using nonoscillatory (Turing) states, the system examined here also differs in performing more logic functions simultaneously.

Logic gates, memory and sensors can also be created by using the slime mold Physarum polycephalum and its protoplasmic tubes.^61,62 Light and heat stimuli affect the frequency of streaming oscillations leading to logic gates derived from the measured frequency change.

Yeast Saccharomyces cerevisiae cultivated in a bioreactor can be used to create a simple AND gate or sensor by taking fatty acids and copper as a input signals.⁶³ This technique does not readily provide small modular blocks and seems to be less suitable for the purpose of universal chemically based computing.

Finally, let us make a remark on the relation of the Turing patterns found in our work to those examined originally by Turing.³ In a recent work aimed at testing the type of bifurcating patterns predicted by Turing against experiments with linear and cyclic arrays of aqueous BZ droplets in oil⁶⁴ five out of six predicted modes have been observed as stable regimes: homogenous oscillations, maximum wavenumber oscillatory and stationary inhomogenous patterns, and intermediate wavenumber oscillatory and stationary inhomogenous patterns. In our case of two cells, the intermediate and maximum wavenumber cases coincide and thus out of the four possible modes we observe only stable homogeneous oscillations and stable inhomogeneous stationary states.

In conclusion, our aim is to point out that the Turing pattern technique may constitute a basis for sensors, memory banks, specially designed processing units and ultimately artificial cellular-scale computers based on combining two-cell units in a lattice. In future such microprocessors might be an interesting solution both for medical and biotechnological purposes.

Acknowledgements

This work was supported by, financial support from specific university research (MSMT no. 21/2012), and grant GACR 203/09/2091.

Notes and references

1. M. Meinhart and A. Gierer, J. Cell Sci., 1974, 15, 321; M. Meinhart and A. Gierer, BioEssays, 2010, 22, 753.
2. S. Kondo and T. Miura, Science, 2010, 329, 1616.
3. A. M. Turing, Philos. Trans. R. Soc., B, 1952, 237, 37.
4. P. K. Maini, R. E. Baker and C.-M. Chuong, Science, 2006, 314, 1397.
5. A. Nakamasu, G. Takahashia, A. Kanbea and S. Kondo, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 8429.
6. A. Badugu, C. Kraemer, P. Germann, D. Menshykau and D. Iber, Sci. Rep., 2012, 2, 991.
7. J. D. Murray, Mathematical Biology II: Spatial Models and Biomedical Applications, Springer Science, Business Media, LLC, USA, 3rd edn, 2003.
8. J. A. Vastano, J. E. Pearson, W. Horsthemke and L. H. Swinney, Phys. Lett. A, 1987, 124, 320.
9. A. Koseska, E. Volkov, A. Zaikin and J. Kurths, Phys. Rev., 2007, 75, 031916.
10. A. Koseska, E. Volkov and J. Kurths, Chaos, 2010, 20, 023132.
11. A. Koseska, A. Zaikin, J. Kurths and J. García-Ojalvo, PLoS One, 2009, 4, 1.
12. V. Castets, E. Dulos, J. Boissonade and P. De Kepper, Phys. Rev. Lett., 1990, 64, 2953.
13. Q. Ouyang, V. Castets, J. Boissonade, J. C. Roux, P. De Kepper and H. L. Swinney, J. Chem. Phys., 1991, 95, 351.
14. K. Agladze, E. Dulos and P. De Kepper, J. Phys. Chem., 1992, 96, 2400–2403.
15. G. Dewel, P. Borckmans, A. De Wit, B. Rudovics, J.-J. Perraud, E. Dulos, J. Boissonade and P. De Kepper, Phys. Stat. Mech. Appl., 1995, 213, 181–198.
16. B. Rudovics, E. Dulos and P. De Kepper, Phys. Scr., 1996, T67, 43–50.
17. B. Rudovics, E. Barillot, P. W. Davies, E. Dulos, J. Boissonade and P. De Kepper, J. Phys. Chem. A, 1999, 103, 1790–1800.
18. K. Asakura, R. Konishi, T. Nakatani, T. Nakano and M. Kamata, J. Phys. Chem. B, 2011, 115, 3959.
19. V. K. Vanag and I. R. Epstein, Phys. Rev. Lett., 2001, 87, 228301.
20. J. Horvath, I. Szalai and P. De Kepper, Science, 2009, 324, 772.
21. H. Ya-Feng, L. Fu-Cheng, F. Wei-Li and D. Li-Fang, Chin. Phys. B, 2012, 21, 034701.
22. M. Toiya, V. K. Vanag and I. R. Epstein, Angew. Chem., Int. Ed., 2008, 47, 7753.
23. M. Toiya, H. O. González-Ochoa, V. K. Vanag, S. Fraden and I. R. Epstein, J. Phys. Chem. Lett., 2010, 1, 1241.
24. J. A. Vastano, J. E. Pearson, W. Horsthemke and H. L. Swinney, Phys. Lett. A, 1987, 124, 320.
25. F. Muzika and I. Schreiber, J. Chem. Phys., 2013, 139, 164108.
26. K. Bar-Eli, Phys. Chem. Chem. Phys., 2011, 13, 11606.
27. M. Dolník and M. Marek, Pulse stimulation of coupled chemical oscillators; Proc. of A Nonlinear Wave Processes in Excitable Media, ed. A.V. Holden, M. Markus and H.G. Othmer, Leeds, 1989, pp. 91–97.
28. R. Avraham and Y. Yarden, Nat. Rev. Mol. Cell Biol., 2011, 12, 104–117.
29. J. Wang and E. Katz, Anal. Bioanal. Chem., 2010, 398, 1591–1603.
30. J. Kosek and M. Marek, J. Phys. Chem., 1993, 97, 120.
31. A. Lekebusch and F. W. Schneider, J. Phys. Chem. B, 1997, 101, 9838.
32. Q. Zhang and H. Shi, J. Theor. Biol., 2012, 314, 164.
33. J. Forster, A. G. Hirst and G. F. Esteban, The ISME Journal, 2013, 7, 28.
34. L. Tsiokas, S. Kim and E.-C. Ong, Cell. Signalling, 2007, 19, 444.
35. D. M. Durand, E.-H. Park and A. L. Jensen, Philos. Trans. R. Soc., B, 2010, 365, 2347.
36. F. Moran and A. Goldbeter, Biophys. Chem., 1984, 20, 149.
37. M. Kubíček and M. Marek, Computational Methods in Bifurcation Theory and Dissipative Structures, Springer-Verlag, New York, 1983.
38. M. Kohout, I. Schreiber and M. Kubíček, Comput. Chem. Eng., 2002, 26, 517.
39. H. G. Othmer and L. E. Scriven, J. Theor. Biol., 1974, 43, 83.
40. J. Řeháček, M. Kubíček and M. Marek, Comput. Chem. Eng., 1998, 22, 283.
41. F. Hynne, S. Danø and P. G. Sørensen, Biophys. Chem., 2001, 94, 121.
42. J. Higgins, Ind. Eng. Chem., 1967, 59, 19.
43. A. D. Nazarea, Proc. Natl. Acad. Sci. U. S. A., 1974, 71, 3751.
44. P. Richards, FEMS Microbiol. Rev., 2003, 27, 547–557.
45. F. Muzika, Ph.D. thesis, Institute of Chemical Technology, Prague, 2014.
46. R. Bartrons, E. V. Schaftinger, S. Vissers and H.-G. Hers, FEBS Lett., 1982, 143, 137.
47. H. M. Sauro and B. N. Kholodenko, Prog. Biophys. Mol. Biol., 2004, 86, 5.
48. M. Barboiu, S. Cerneaux, A. van der Lee and G. Vaughan, J. Am. Chem. Soc., 2004, 126, 3545.
49. B. S. Khakh and R. A. North, Nature, 2006, 442, 527.
50. S. Locovei, J. Wang and G. Dahl, FEBS Lett., 2006, 580, 239.
51. D. G. Gibson, J. I. Glass, C. Lartigue, V. N. Noskov, R.-Y. Chuang, M. A. Algire, G. A. Benders, M. G. Montague, L. Ma, M. M. Moodie, Ch. Merryman, S. Vashee, R. Krishnakumar, N. Assad-Garcia, C. Andrews-Pfannkoch, E. A. Denisova, L. Young, Z.-Q. Qi, T. H. Segall-Shapiro, C. H. Calvey, P. P. Parmar, C. A. Hutchison III, H. O. Smith and J. C. Venter, Science, 2010, 329, 52.
52. V. N. Noskov, B. J. Karas, L. Young, R.-Y. Chuang, D. G. Gibson, Y.-C. Lin, J. Stam, I. T. Yonemoto, Y. Suzuki, C. Andrews-Pfannkoch, J. I. Glass, H. O. Smith, C. A. Hutchison III, J. C. Venter and P. D. Weyman, ACS Synth. Biol., 2012, 1, 267.
53. A. Hjelmfelt, F. W. Schneider and J. Ross, Science, 1993, 260, 335.
54. A. Hjelmfelt and J. Ross, J. Phys. Chem., 1993, 97, 1988.
55. A. Hjelmfelt and J. Ross, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 63.
56. J. J. Hopfield, Proc. Natl. Acad. Sci. U. S. A., 1984, 81, 3088.
57. A. Hjelmfelt and J. Ross, Phys. D, 1995, 84, 180.
58. P. H. King, J. C. Corsi, B.-H. Pan, H. Morgan, M. R. R. de Planque and K.-P. Zauner, BioSystems, 2012, 109, 18.
59. J. Gorecki, J. N. Gorecka and A. Adamatzky, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 042910.
60. J. Holley, I. Jahan, B. D. L. Costello, L. Bull and A. Adamatzky, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 056110.
61. J. G. H. Whiting, B. P. J. de Lacy Costello and A. Adamatzky, BioSystems, 2014, 119, 45.
62. A. Adamatzky and T. Schubert, Mater. Today, 2014, 17, 86.
63. W. S. Teo and M. W. Chang, Biotechnol. Bioeng., 2014, 111, 144.
64. N. Tompkins, N. Li, C. Girabawe, M. Heymann, G. B. Ermentrout, I. R. Epstein and S. Fraden, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 4397.

---