Tuning the magnetism of a ZrS2 monolayer by substitutional doping
Abstract
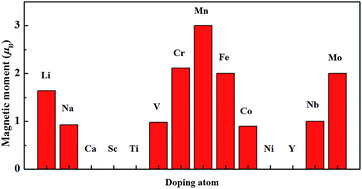
In view of the important role of developing efficient approaches to induce and manipulate the magnetism in semiconducting transition metal dichalcogenide monolayers for their application in low-dimensional spintronic devices, the influence of a series of transition metal (TM) (Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Y, Nb and Mo), alkali metals (Li and Na) and alkaline-earth (Ca) dopants on the electronic structure and magnetic properties of a ZrS2 monolayer are investigated using first-principles calculations. It is shown that Ca, Sc, Ti, Ni and Y dopants cannot induce the magnetism in the doped ZrS2 monolayer and the stability of the magnetic state of the Na doped system is very small, while the ground state of Li, V, Cr, Mn, Fe, Co, Nb and Mo-doped systems are magnetic and the magnetic moment induced by 3d TM, 4d TM and Li dopants are mainly contributed by the 3d states of the 3d TM atom, the 4d states of the 4d TM atom and its nearing Mo atoms, and the 3p states of the S atoms and the interstitial region around Li, respectively. The evolutions of the magnetic moments with the different TM dopants, such as Ti, V, Cr, Mn, Fe, Co, Ni, Nb and Mo, can be interpreted in terms of a simple analysis based on the molecular orbitals and electron filling. Furthermore, the magnetic coupling between the moments induced by two Li, V, Cr, Fe, Co, Nb and Mo is long-range ferromagnetic and the coupling can be attributed to the hybridization interaction involving polarized electrons or holes, whereas the coupling between the moments induced by two Mn is anti-ferromagnetic. The calculated results suggest that substitutional doping of Li, V, Cr, Fe, Co and Mo atoms can induce the room temperature ferromagnetism in the ZrS2 monolayer.

 Please wait while we load your content...
Please wait while we load your content...