Open Access Article
Open Access ArticleA statistical thermodynamics model for monolayer gas adsorption on graphene-based materials: implications for gas sensing applications
H. H. Pua,
S. H. Rhimb,
M. Gajdardziksa-Josifovskab,
C. J. Hirschmuglb,
M. Weinert*b and
J. H. Chen*a
aDepartment of Mechanical Engineering and Laboratory for Surface Studies, University of Wisconsin-Milwaukee, Milwaukee, WI 53211, USA. E-mail: jhchen@uwm.edu
bDepartment of Physics and Laboratory for Surface Studies, University of Wisconsin-Milwaukee, Milwaukee, WI 53211, USA. E-mail: weinert@uwm.edu
First published on 10th September 2014
Abstract
Field-effect transistor-based conductance gas sensors are attracting considerable research interest because of their miniaturized size, high sensitivity, and portability. Here, we propose statistical thermodynamics models to analytically characterize monolayer gas molecule adsorption on crystalline and amorphous solid surfaces in terms of adsorption density and coverage, respectively, which are critical for gas sensing applications. By testing the monolayer adsorption of gas molecules, such as CO, NO, NH3 and NO2, on graphene and reduced graphene oxide (rGO), we found that adsorption density and coverage can be estimated from only the binding energy of gas molecules with a high accuracy compared with the exact values obtained by solving the Schrödinger equation. Moreover, the experimentally observed (e.g., NO2) density on graphene is close to our theoretical prediction. The proposed approaches to quantitatively characterize gas adsorption on solid surfaces are of great significance to help understand and optimize the performance of gas sensors.
1 Introduction
Gas sensing has attracted significant attention across various research communities because of its potential applications in detecting air pollutants, toxic gas leakage in facilities, specific gas generation during chemical reactions of interest, etc.1 In principle, gas sensing can be achieved by transducing the signals from the interactions between the gas molecules and sensing platforms. Numerous types of gas sensors have been designed such as the optical gas sensor,2 magnetic gas sensor,3 surface acoustic wave gas sensor4 and conductance (or resistance) gas sensor.5 Among these, field-effect transistor-based conductance gas sensors have now been miniaturized to the nanoscale and are attracting increased interest due to their convenient fabrication, sensitive detection, and portability. The sensing materials now include two-dimensional metal6 or metal oxide thin films,7,8 arrays of their zero-dimensional nanospheres or one-dimensional nanorods,7,9–18 graphene,19–21 rGO,22,23 carbon nanotubes (CNTs)24,25 and their hybrid structures with various nanoparticles.5,26–29 The conductance gas sensor works by bridging two electrodes (source and drain) with sensing materials and applying current through them. Gas detection can be realized by monitoring the current change upon exposure to the target gas environment under a constant voltage. A critical performance index of a gas sensor is the high sensitivity or lower detection limit. The sensitivity of a sensing material is directly determined by the ratio of change in conductance before and after gas adsorption to its conductance in the absence of target gases. However, indirectly or fundamentally, sensitivity is dictated by the inter-correlated quantities of interaction strength (i.e., between the gas molecules and the sensing materials) and the adsorption density or coverage. The stronger the interaction, more gas molecules will be adsorbed (i.e., higher adsorption density or coverage). Consequently, sensitivity can be effectively enhanced either by increasing the target gas concentration or by strengthening the gas-surface interactions.In principle, gas molecules could interact with solid surfaces via either van der Waals attraction or by a chemical reaction. Although both would vary the conductance of the solid, the van der Waals interaction could be used for gas sensing applications, while the chemical reaction would be more suitable for catalysis. Upon the adsorption of gas molecules, the electronic structure of the sensing material will be altered and its conductance will change. For physical adsorption on a crystalline surface, especially at low density, electronic structure is modified in such a manner that only the Fermi level is tuned with the band dispersions remaining invariant,30 i.e., the carrier mobility remains unchanged. For example, graphene can be n-type or p-type doped with the Dirac cone intact through charge transfer, depending on whether the gas species is reducing or oxidizing.30 Considering that conductivity is linearly proportional to the product of carrier concentration and mobility, its variation originates dominantly from the change in carrier concentration correlated with the amount of adsorbed gas molecules for gas sensing. However, the recovery rate would be quite slow (i.e., the adsorbed gas molecules are sluggish in detaching from the sensing material) if sensitivity is enhanced by increasing the interaction strength. For example, with the surface oxidized silver-based gas sensor, the response and recovery times toward 1% NH3 and 1250 ppm NO2 detections are ∼150 s and ∼200 s, ∼100 s and ∼1200 s, respectively.31 The prominent difference in the recovery time arises from the stronger interaction between NO2 and the oxidized silver surface by forming the NO3 complex.31 To overcome this barrier and obtain high sensitivity and fast recovery simultaneously, judicious routes include searching for new materials whose conductivity is ultrasensitive to external perturbations, in which case only weak gas adsorption is necessary (e.g., graphene is ultrasensitive to NO2 molecules and even a single molecule21); and accelerating gas desorption by a gate voltage23 or ultraviolet light irradiation32 because both can effectively lower the energy barrier for gas molecules to detach. In either case, it is desirable to characterize gas adsorption both qualitatively and quantitatively at the starting point to identity potential candidates for gas sensing and tailor their performance.
Currently, however, the theoretical methodology to predict gas adsorption depends on adsorption site, binding energy, and charge transfer. Gas molecules tend to adsorb on sites with higher binding energies. The current consensus is that a higher binding energy (i.e., more charge transfer/redistribution) favors higher sensitivity. However, the binding energy only provides qualitative evidence and cannot provide further insights into how gas sensitivity is intimately related to binding energy in a more specific manner that is suitable for gas sensing modeling. Quantitatively, both Touzik et al.33 and Lin et al.34 studied adsorption capacity on graphitic surfaces. Their approaches require the cumbersome procedures of fitting the gas-surface interaction potential predicted by the ab initio calculations and analytically solving the Schrödinger equation. Practically, it would be encouraging to characterize the adsorption capacity more conveniently with multiple benefits. On one hand, an easy way facilitates the evaluation of gas adsorption capability of various materials by circumventing the above mentioned cumbersome procedures and helps in the performance tuning of gas sensors in a controllable fashion. On the other hand, the derived simple-to-use expression for gas adsorption capacity can be integrated into the conductivity model for a specific material (e.g., CNTs,35 graphene36 and its nanoribbons37) to faithfully represent the gas-surface interactions, establishing the model that gas sensing can be fundamentally understood in a multifunctional manner such that even the concentration of target gases can be detected as opposed to identifying the presence of gas species only. Finally, the approach can also be applied beyond gas sensing and for fields, such as gas storage, or even surface catalytic reactions under certain conditions.
Herein, we investigate gas adsorptions on solid surfaces for the convenient characterization of gas adsorption capabilities. Despite various sensing materials, their surfaces can be categorized only into two types: crystalline vs. amorphous. Graphene and rGO are used as pilot sensing materials because of their large surface to volume ratio and because they represent crystalline and amorphous gas adsorption surfaces, respectively. The statistical thermodynamics analysis was developed to establish the model of gas adsorption density on graphene or coverage on rGO with parameter inputs from density functional theory (DFT) calculations. We found that gas adsorption density or coverage can be quantified accurately with the only unknown parameter of the binding energy of gas molecules that can be determined either theoretically or experimentally. Our findings essentially simplified the method to estimate the gas adsorption capabilities of solid surfaces and are significant in exploring future potential candidates for gas sensing. For proof of principles, we focused only on the low concentration of four target gas species, CO, NO, NH3 and NO2, diluted in atmosphere air (1 ppm) with the assumption that the sensors were operated at room temperature (300 K).
2 Methods
2.1 First principles calculations
The DFT calculations were carried out using the code OPENMX.38 The pseudo atomic orbitals (PAOs) were used to expand the single electron wave function and were specified by X7.0-s2p2, where X is the elements H, C, N and O, 7.0 represents the cutoff atomic radius in Bohr and s2p2 indicates that the basic functions are expanded by two primitive orbitals of individual s and p orbitals, respectively. Norm conserving pseudopotential was used with the treatment of an exchange-correlation functional in the formalism of generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE)39 for CO and NH3 without spin and for NO and NO2 with spin polarizations. The 3 × 3 supercell composed of the centered rectangular unit cell of graphene and layer spacing larger than 20 Å was used for single gas molecule adsorption such that interactions could be ignored between the adjacent layers and between the molecules themselves due to periodic boundary conditions. The numerical integrations were performed with a cut-off energy of 2720 eV in real space and a k-point density of 0.02 Å−1 in the reciprocal space. The structural relaxations were terminated with a force criteria of 0.01 eV Å−1.Despite its significant success in predicting several properties of solids and molecules, one drawback of the Kohn–Sham DFT is its failure in describing long range electron–electron correlations that give rise to the van der Waals force (i.e., the attractive dispersion force) responsible for weak interactions among molecules and solids. In general, the common GGA functionals would severely underestimate this long range correlation, and this problem still exists even for the hybrid functionals by replacing part of the local with nonlocal Hartree–Fock exchange term.40 For the gas adsorption systems considered here, it is significant to include this van der Waals force in faithfully quantizing adsorption density or coverage. To realize this, we adopted the modified version of the DFT-D method41 in the semiempirical GGA functional to incorporate this dispersion force using the damped atom pairwise dispersion corrections in the form of C6·R−6, which has been shown to be very successful in describing medium to large range interactions.42
2.2 Statistical thermodynamics modeling
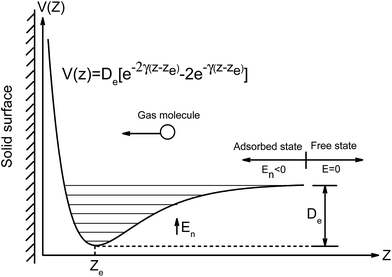
For physical adsorption, gas molecules are attracted to solid surfaces forming the adsorption layer. Depending on gas concentration, it could be multilayer or monolayer adsorption. Usually, the Langmuir adsorption isotherm is used to characterize gas adsorption in terms of coverage (defined as the fraction of sites occupied). At low coverage, the spreading pressure of the adsorbed gas is equal to its partial pressure before adsorption and the coverage is linearly proportional to pressure. Under this circumstance, the coverage could be reformulated in terms of per unit area and rephrased as density, which is also known as the Henry adsorption isotherm. When gas concentration increases, the coverage will become nonlinear and asymptotic to unity. Here, we develop the statistical thermodynamics modeling to establish the Langmuir (or Henry) adsorption constant with inputs from DFT calculations.Considering a single gas molecule approaching the solid surface in the free state, as illustrated in Fig. 1, it will be trapped onto the surface due to the attractive van der Waals force. For homogeneous solid surfaces, the potential energy between the gas molecule and the solid surface can be considered to be independent of adsorption sites across the surface defined in the x–y plane. Thus, the interaction energy can be represented by the Morse potential only in the z direction as
 | (1) |
 | (2) |
In the framework of equilibrium approach, the energies of the adsorbed gas molecules are in the Boltzmann distribution and the movements of molecules among the energy levels inside the potential well are treated as the random walk process. For monolayer gas adsorption with low coverage, the energy levels close to the bottom of the potential well are mostly occupied. For the mobile adsorbed phase, the gas molecules will only vibrate in the z direction but are free to diffuse in the xy-plane. Then, the canonical ensemble partition function for a single adsorbed gas molecule is44
 | (3) |
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(λ3/kBT). Thus, we can obtain the gas adsorption density ng from eqn (3) and (4) as
ln(λ3/kBT). Thus, we can obtain the gas adsorption density ng from eqn (3) and (4) as
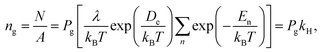 | (5) |
For nonhomogeneous surfaces with distinct adsorption sites, gas molecules are inclined to be localized to the sites with the largest binding energy. Alternatively, the generalized Langmuir equation can be adopted to estimate the coverage θi of the different types of adsorption sites at equilibrium as opposed to the adsorption density of the homogeneous surface. The total coverage θ is
 | (6) |
 | (7) |
 | (8) |
 .45 Using the definition of ωg, eqn (7) can also be formulated as
.45 Using the definition of ωg, eqn (7) can also be formulated as
 | (9) |
3 Results and discussions
To invoke eqn (5) for gas sensing applications, we start with gas adsorption on graphene and relax the system using the optimized molecular orientations and adsorption sites predicted by Leenaerts et al.30 Fig. 2(a) shows the predicted adsorption density of CO, NO, NH3 and NO2 on graphene. As we can see, the adsorption densities of CO (0.13 × 109 cm−2), NO (0.87 × 1010 cm−2) and NH3 (0.62 × 109 cm−2) are close to each other, while that of NO2 (0.99 × 1012 cm−2) is strikingly greater by about 2 to 3 orders of magnitude. The substantially enhanced adsorption density for NO2 is largely attributed to its deeper potential well depth or higher binding energy of 0.214 eV compared with 0.086 eV for CO, 0.147 eV for NO, and 0.112 eV for NH3 because the occupying number of oscillators in the Boltzmann distribution will increase drastically with increasing energy. We could also project the predicted adsorption densities into the primitive cell of graphene, which are 0.25 × 10−8 per cell, 0.17 × 10−6 per cell, 0.12 × 10−7 per cell and 0.19 × 10−4 per cell for CO, NO, NH3 and NO2, respectively, suggesting dilute adsorptions. Because of its homogeneous surface, these gas species have been shown to possess similar binding energy on different adsorption sites (top, bridge and hollow),30,34 namely, low migration energy barriers. Thus, the use of eqn (5) to calculate adsorption densities for these gases is reasonable. | ||
| Fig. 2 Characteristics of CO, NO, NH3 and NO2 adsorption on graphene and rGO. (a) Exact (estimated) gas adsorption densities ng (n′g) from eqn (5) [eqn (10)] on graphene with the relative error R shown in the inset. (b) Upper panel: the exact (estimated) gas adsorption coverage θ (θ′) from eqn (6), (8) and (9) [eqn (6), (8) and (11)] for ether, carbonyl and epoxide in rGO, respectively; Lower panel: the relative errors R for ether, carbonyl and epoxide, respectively. | ||
Experimentally, the hole concentration induced by NO2 (1 ppm) adsorption on graphene21 has been measured to be around 0.5 × 1011 cm−2. Each NO2 molecule can attract about 0.14e from graphene by the Mulliken charge analysis in our calculation and about 0.099e by the Hirshfeld charge analysis.30 Thus, the adsorption density of NO2 is estimated to be around 0.42 × 1012 cm−2. Although our prediction of the adsorption density of NO2 is close to the experimental value, we should be aware that a small discrepancy could stem from the following aspects. On one hand, the DFT calculations even with the treatment of dispersion force can only approach the exact adsorption energy of the adsorbates on surfaces (slight overestimation or underestimation cannot be avoided). On the other hand, the calculations were carried out at 0 K, which would also result in small overestimation of gas adsorption energy compared with the case that sensors are practically operating around room temperature. Moreover, the effects of molecular rotations and intramolecular vibrations on the adsorption are neglected, leading to the increased adsorption probability of gas molecules approaching the surface. (This effect will be accounted for in later sections.)
Because graphene is mostly sensitive to NO2 and relatively resistant to CO, NO and NH3, as demonstrated above, it is intriguing to structurally modify graphene and design new gas sensors toward these three insensitive gases. rGO, as the derivative of graphene by reducing GO thermally or chemically, provides an opportunity for gas sensing as well with its manipulative oxygen-containing groups via controlling the reduction conditions. Despite the fact that the main functional groups in GO are epoxide and hydroxyl, the remaining oxygen atoms in rGO are in the forms of ether, carbonyl and epoxide groups.46 Therefore, we also consider the effects of these three functional groups inside the carbon plane on gas sensing. Because rGO is structurally nonstoichiometric and amorphous due to the random distribution of functional groups, eqn (6)–(9) are used to characterize the gas adsorption coverage for individual functional groups.
Fig. 2(b) shows the coverage of CO, NO, NH3 and NO2 on rGO with ether, carbonyl and epoxide. For ether, the coverage is 0.17 × 10−5, 0.84 × 10−5, 0.72 × 10−4 and 0.84 × 10−3 for CO, NO, NH3 and NO2, respectively, while for carbonyl, the coverage is 0.12 × 10−5, 0.22 × 10−2, 0.42 × 10−3 and 0.35 × 10−5 for CO, NO, NH3 and NO2, respectively. Epoxide can only physically attract CO, NH3 and NO2 with a coverage of 0.29 × 10−5, 0.78 × 10−5 and 0.79 × 10−6, while NO will react with epoxide-forming NO2. Hence, ether in rGO can considerably enhance the sensitivity to NH3 and NO2 and carbonyl in rGO can greatly enhance the sensitivity to NO and NH3. However, epoxide is less attractive to NO2. In addition, NO will bond with the oxygen atom in epoxide to form NO2 and then adsorb on the underlying carbon plane in a manner similar to the adsorption of NO2 on graphene. As the epoxide groups tend to aggregate together,47 NH3 is physically absorbed in the epoxide rich region, as considered here. However, it has also been shown that NH3 can be dissociated by a single epoxide into the OH and NH2 species.48 The increased coverage of NH3 on both ether and carbonyl is due to the H bond between H atoms in NH3 and O atoms in the functional groups. Nonetheless, the enhanced coverage of NO is because of the tendency to form an NO2 complex between the NO molecule and the carbonyl group. NO2 is attracted to ether with oxygen atoms pointing to it, unlike the NO3 complex between NO2 and carbonyl on the edge of rGO34 or between NO2 and metal oxide surfaces.31 These results suggest that rGO can be a good candidate for gas sensing toward NO, NH3 and NO2, which is consistent with experimental observations.22,23
Note that two parameters De and En in eqn (5) and De and γ in eqn (9) are required to obtain adsorption density and coverage, respectively. Potential well depth De, equivalent to the binding energy of a single gas molecule on a solid surface, can be determined experimentally49 or theoretically.30,34 However, energy level En and the fitting parameter γ can only be obtained by fitting the Morse potential and then solving the Schrödinger equation with it. For practical purposes, it is convenient to estimate the gas adsorption density or coverage without the need of fitting the Morse potential and solving the Schrödinger equation.34 To this end, we found that eqn (5) and (9) can be reformulated by removing En and γ as.
 | (10) |
 | (11) |
Accordingly, the estimated adsorption densities from eqn (10) are presented in Fig. 2(a). Compared with the exact values from eqn (5), we can see that the absolute discrepancies are less than 26%. It can also be seen from Fig. 2(b) that the estimated coverage values by inserting eqn (11) into eqn (7) are very close to the exact values for NO adsorbed on carbonyl and NO2 on both ether and carbonyl. Although CO and NH3 have the largest relative error (<15%), the errors are within ±8% for all the other gas species. Thus, we can conclude that the potential well depth De (binding energy) can solely be used to determine the adsorption density and coverage with a high accuracy.
In general, as stated above, a gas molecule is adsorbed to the surface with negative energy values. For low concentration of gas molecules and abundant adsorption sites, the mutual interactions between the adsorbed molecules can be ignored because the molecular distance is quite large. Thus, adsorption density should be governed by gas concentration for the same type of solid surface, e.g., graphene as we considered here, and is irrespective of the magnitude of the potential well depth. However, this is clearly not the case as expected and shown above for the four target gases. In essence, this partial adsorption originates from the fact that not every individual incoming gas molecule can be attracted to the solid surface, taking into account the thermal fluctuations of both gas molecules and the solid surface, as shown in the Boltzmann factor in eqn (5), (9), (10) and (11). Alternatively, we could also understand this effect in terms of the thermally averaged sticking coefficient of gas molecules approaching the solid surface, which is derived as the implicit function of adsorption energy ε50
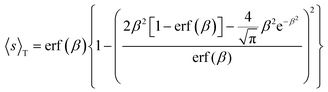 | (12) |
 and
and 
The resultant room temperature sticking coefficients with respect to adsorption energy for gas molecules, CO, NO, NH3 and NO2, on both graphene and rGO are also illustrated in Fig. 3. We can see that the sticking coefficient increases and becomes saturated to unity when the adsorption energy is sufficiently high. Saturation can be anticipated because the higher the adsorption energy is, its less likely that the gas molecule would be bounced off the surface due to the thermal vibrations of the surface atoms. Classically, the adsorption rate constant is the arriving rate of gas molecules of (kBT/2πmg)1/2 regardless of the adsorption energy. Pagni and Keck45 have shown that both the steady state and the equilibrium adsorption rate constant increases with respect to adsorption energy and are greater than their classical counterparts at higher adsorption energy, although the critical energy depends on the masses and the characteristic frequencies of both the gas molecules and the surface atoms of the adsorption sites. When the upper limit is specified for each gas with the potential well depth De from our calculations, in contrast with the NO2 adsorption on graphene, CO, NO and NH3 have smaller coefficients due to their weaker physical binding to graphene. However, situations are quite different for adsorptions on ether and carbonyl in rGO. While NO and NH3 have an enhanced sticking coefficient when attracted toward both of them, CO (NO2) is only more (less) attractive to ether (carbonyl). These results are coherently consistent with the analysis from the perspectives of adsorption density and coverage.
Recall that eqn (5) and (10) are only valid for monolayer gas adsorption with low density within the ideal gas approximation, it is essential to estimate the dynamic range of target gas concentration within which our model is valid. Assuming that the predicted gas adsorption density is no greater than the area density of air at room temperature (0.85 × 1013 cm−2), the upper limit of target gas concentration can be estimated. For example, the upper bound concentrations for CO, NO and NH3 diluted in air are estimated to be ∼6.5%, 977 ppm and 1.4%, respectively. For NO2, however, it is extrapolated to be ∼8.5 ppm (and ∼20.2 ppm according to the experimentally observed adsorption density21). Beyond these upper bounds, multilayer adsorption occurs, in which the adsorbed gas could be in the compressed phase with a higher pressure than its partial pressure in the free state, and cannot be treated as the ideal gas any more. Thermodynamically obtaining the gas pressure for an imperfect gas in the adsorption layer is a prerequisite to determine adsorption density. For localized adsorptions on nonhomogeneous surfaces, multilayer adsorption occurs until all the types of adsorption sites are fully occupied and the critical concentration is dependent on the fractions of each type of site. The adsorbed gas pressure also needs to be determined thermodynamically. Then, the Brunauer–Emmett–Teller (BET) equation should be used instead of eqn (6) to estimate coverage. In addition, it should be noted if the diffusion energy barriers are high on the crystalline surface, which is common on metal or metal oxide surfaces, the adsorbed gas molecules cannot be treated as mobile phase anymore. In that case, the Henry adsorption constant would involve the partition functions along both perpendicular and parallel directions to the surface. While the former can still be treated using the procedure stated in the Methods section, the latter has to be identified by harmonic oscillator approximation (details will be presented elsewhere).
4 Conclusions
The interactions between monolayer gas molecules and solid surfaces have been investigated for gas sensing applications. Depending on whether gas molecules can be mobile on homogeneous surfaces or localized to certain adsorption sites on nonhomogeneous surfaces (that are usually located at imperfections, such as the defects and edges, along the material or the micropores within it), statistical thermodynamic models are developed to characterize the monolayer gas adsorption density and coverage, respectively. With inputs from the first-principles calculations, the adsorptions of four target gas species, CO, NO, NH3 and NO2, are studied on homogeneous graphene and nonhomogeneous rGO surfaces. Our results show that graphene is more sensitive to NO2, while NO (NO2) prefers to be attached to carbonyl (ether) in rGO. In addition, NH3 can be moderately attracted to both graphene and rGO, whereas CO shows a very weak attraction for both the surfaces. Although the derived analytical expressions require fitting the Morse potential and solving the Schrödinger equation in the first place, we found that adsorption density and coverage can be effectively estimated by only the binding energy of a gas molecule with high accuracy. This is desirable and significant because binding energy can be determined either experimentally or theoretically. Within our knowledge of a literature survey on experimental data, we could only obtain the experimentally extracted adsorption density for NO2 on graphene (0.42 × 1012 cm−2),21 close to our prediction (0.99 × 1012 cm−2). Our proposed approaches to quantify the monolayer gas adsorption in terms of density on a homogeneous surface and coverage on a nonhomogeneous surface present solid evidence to qualitatively assess the performance of gas sensing. They also provide a means to understand and determine the gate voltage required to enhance gas sensitivity (or recovery rate but with the sign of the voltage reversed), which varies the gas surface interaction strength. Moreover, they help to identify the contributions from distinctive types of adsorption sites that are important in manipulating gas sensing performance through structural modification; for example, the contributions of functional groups in rGO can be obtained by their individual species weight determined from microscopic techniques and the calculated gas adsorption coverage toward specific gas.Acknowledgements
The authors acknowledge financial support from the National Science Foundation (CMMI-0856753 and CMMI-0900509) and the Research Growth Initiative Program of the University of Wisconsin-Milwaukee (UWM).Notes and references
- G. Eranna, B. C. Joshi, D. P. Runthala and R. P. Gupta, Crit. Rev. Solid State Mater. Sci., 2004, 29, 111–188 CrossRef CAS.
- M.-K. Bae, J. A. Lim, S. Kim and Y.-W. Song, Opt. Express, 2013, 21, 2018–2023 CrossRef CAS PubMed.
- A. Punnoose, K. M. Reddy, J. Hays, A. Thurber and M. H. Engelhard, Appl. Phys. Lett., 2006, 89, 112509 CrossRef.
- W. P. Jakubik, M. Urbanczyk, E. Maciak and T. Pustelny, Bull. Pol. Acad. Sci.: Tech. Sci., 2008, 56, 133–138 CAS.
- S. Cui, S. Mao, G. Lu and J. Chen, J. Phys. Chem. Lett., 2013, 4, 2441–2454 CrossRef CAS.
- J. F. Chang, H. H. Kuo, I. C. Leu and M. H. Hon, Sens. Actuators, B, 2002, 84, 258–264 CrossRef CAS.
- J. L. Solis, S. Saukko, L. Kish, C. G. Granqvist and V. Lantto, Thin Solid Films, 2001, 391, 255–260 CrossRef CAS.
- H. Tang, K. Prasad, R. Sanjines and F. Levy, Sens. Actuators, B, 1995, 26, 71–75 CrossRef CAS.
- J. Chen, L. N. Xu, W. Y. Li and X. L. Gou, Adv. Mater., 2005, 17, 582–586 CrossRef CAS.
- E. Comini, G. Faglia, G. Sberveglieri, Z. W. Pan and Z. L. Wang, Appl. Phys. Lett., 2002, 81, 1869–1871 CrossRef CAS.
- T. Gao and T. H. Wang, Appl. Phys. A, 2005, 80, 1451–1454 CrossRef CAS.
- J.-H. Lee, Sens. Actuators, B, 2009, 140, 319–336 CrossRef CAS.
- W. Y. Li, L. N. Xu and J. Chen, Adv. Funct. Mater., 2005, 15, 851–857 CrossRef CAS.
- X. L. Li, T. J. Lou, X. M. Sun and Y. D. Li, Inorg. Chem., 2004, 43, 5442–5449 CrossRef CAS PubMed.
- A. Ponzoni, E. Comini, G. Sberveglieri, J. Zhou, S. Z. Deng, N. S. Xu, Y. Ding and Z. L. Wang, Appl. Phys. Lett., 2006, 88, 203101 CrossRef.
- M. Tiemann, Chem.–Eur. J., 2007, 13, 8376–8388 CrossRef CAS PubMed.
- Q. Wan, Q. H. Li, Y. J. Chen, T. H. Wang, X. L. He, J. P. Li and C. L. Lin, Appl. Phys. Lett., 2004, 84, 3654–3656 CrossRef CAS.
- J. T. Zhang, J. F. Liu, Q. Peng, X. Wang and Y. D. Li, Chem. Mater., 2006, 18, 867–871 CrossRef CAS.
- B. Huang, Z. Li, Z. Liu, G. Zhou, S. Hao, J. Wu, B.-L. Gu and W. Duan, J. Phys. Chem. C, 2008, 112, 13442–13446 CAS.
- G. Ko, H. Y. Kim, J. Ahn, Y. M. Park, K. Y. Lee and J. Kim, Curr. Appl. Phys., 2010, 10, 1002–1004 CrossRef.
- F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652–655 CrossRef CAS PubMed.
- G. Lu, L. E. Ocola and J. Chen, Nanotechnology, 2009, 20, 445502 CrossRef PubMed.
- G. Lu, K. Yu, L. E. Ocola and J. Chen, Chem. Commun., 2011, 47, 7761–7763 RSC.
- J. Li, Y. J. Lu, Q. Ye, M. Cinke, J. Han and M. Meyyappan, Nano Lett., 2003, 3, 929–933 CrossRef CAS.
- L. Valentini, I. Armentano, J. M. Kenny, C. Cantalini, L. Lozzi and S. Santucci, Appl. Phys. Lett., 2003, 82, 961–963 CrossRef CAS.
- S. Deng, V. Tjoa, H. M. Fan, H. R. Tan, D. C. Sayle, M. Olivo, S. Mhaisalkar, J. Wei and C. H. Sow, J. Am. Chem. Soc., 2012, 134, 4905–4917 CrossRef CAS PubMed.
- A. Kaniyoor, R. I. Jafri, T. Arockiadoss and S. Ramaprabhu, Nanoscale, 2009, 1, 382–386 RSC.
- H. Song, L. Zhang, C. He, Y. Qu, Y. Tian and Y. Lv, J. Mater. Chem., 2011, 21, 5972–5977 RSC.
- A. Star, V. Joshi, S. Skarupo, D. Thomas and J.-C. P. Gabriel, J. Phys. Chem. B, 2006, 110, 21014–21020 CrossRef CAS PubMed.
- O. Leenaerts, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125416 CrossRef.
- S. M. Cui, H. H. Pu, E. C. Mattson, G. H. Lu, S. Mao, M. Weinert, C. J. Hirschmugl, M. Gajdardziska-Josifovska and J. H. Chen, Nanoscale, 2012, 4, 5887–5894 RSC.
- T. Hara, T. Ishiguro and K. Shinozaki, Jpn. J. Appl. Phys., 2011, 50, 041502 CrossRef.
- A. Touzik and H. Hermann, Chem. Phys. Lett., 2005, 416, 137–141 CrossRef CAS.
- X. Lin, J. Ni and C. Fang, J. Appl. Phys., 2013, 113, 034306 CrossRef.
- F. Deng and Q.-S. Zheng, Appl. Phys. Lett., 2008, 92, 071902 CrossRef.
- N. M. R. Peres, A. H. C. Neto and F. Guinea, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195411 CrossRef.
- D. Gunlycke, D. A. Areshkin and C. T. White, Appl. Phys. Lett., 2007, 90, 142104 CrossRef.
- T. Ozaki, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155108 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. Hobza, J. Sponer and T. Reschel, J. Comput. Chem., 1995, 16, 1315–1325 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- T. Barakat, K. Abodayeh and O. M. Al-Dossary, Czech J. Phys., 2006, 56, 583–590 CrossRef CAS.
- T. L. Hill, An introduction to statistical thermodynamics, Addison-Wesley publishing company, INC., 1960 Search PubMed.
- P. J. Pagni and J. C. Keck, J. Chem. Phys., 1973, 58, 1162 CrossRef CAS.
- S. Mao, H. Pu and J. Chen, RSC Adv., 2012, 2, 2643–2662 RSC.
- W. Cai, et al., Science, 2008, 321, 1815–1817 CrossRef CAS PubMed.
- E. C. Mattson, K. Pande, M. Unger, S. Cui, G. Lu, M. Gajdardziska-Josifovska, M. Weinert, J. Chen and C. J. Hirschmugl, J. Phys. Chem. C, 2013, 117, 10698–10707 CAS.
- S. E. Weber, S. Talapatra, C. Journet, A. Zambano and A. D. Migone, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 13150–13154 CrossRef CAS.
- U. Leuthausser, Z. Phys. B: Condens. Matter, 1981, 44, 101 CrossRef.
| This journal is © The Royal Society of Chemistry 2014 |