Influence of nanoparticle properties on the thermal conductivity of nanofluids by molecular dynamics simulation
Abstract
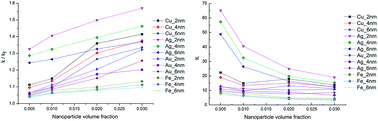
The properties of nanoparticles (including shape, size, material, and volume concentration) may significantly influence the thermal properties of nanofluids. Through molecular dynamics simulations, the aim of this study is to investigate the influence of nanoparticle properties on the thermal conductivity of nanofluids and find an effective criterion for predicting thermal conductivity enhancement. By establishing a series of simulation models, thermal conductivities of nanofluids were calculated on the basis of the Green–Kubo formula. It was found that all the nanoparticle properties that have been considered in this work influence the thermal conductivity of nanofluids, and the influence rules were discussed. Furthermore, there is a positive correlation between the distribution of atomic potential energy and the thermal conductivity of nanofluids. Therefore, the ratio of energetic atoms in nanoparticles is proposed to be the criterion for predicting enhancement of the apparent thermal conductivity of nanofluids.

 Please wait while we load your content...
Please wait while we load your content...