Preparation and topological properties of two structures with p-sulfobenzoic ligands and Zn²⁺ and Mn²⁺ ions

Abstract

There has been recent interest in coordinated polymers due to their structural and topological properties; therefore, the search for efficient synthesis processes to construct these materials by exploiting different organic ligands has intensified. In this context, two coordinated polymers (Zn–psb and Mn–psb) consisting of p-sulfobenzoic acid and either Zn²⁺ or Mn²⁺ ions, respectively, were synthesized by crystallization in gel using ethambutol hydrochloride as a new crystallization agent. Both compounds crystallized in the triclinic system and space group P1̄ and have similar unit cell volumes with a difference of 2%. The crystal data for Zn–psb: a = 8.080(4) Å, b = 11.385(6) Å, c = 12.282(6) Å, α = 97.402(4)°, β = 106.530(4)°, and γ = 110.445(5)°; and for Mn–psb: a = 8.055(5) Å, b = 10.152(7) Å, c = 12.541(8) Å, α = 99.084(6)°, β = 95.358(5)°, and γ = 106.090(6)°. Despite the structural similarity, two different networks (tfz-d and pcu for Zn–psb and Mn–psb, respectively) were formed, and their topological properties were explored by reticular chemistry.

---

Introduction

The literature describes several compounds involving carboxylate ligands and transition metal sites.^1–5 These complexes have received special attention recently due to their potential applications in gas adsorption,^6–8 catalysis^9,10 and magnetic properties.^11–13 In this sense, these materials exhibit many applications with interesting physical chemical properties, with the size of cages ranging from 0.9 to 3.4 nm.^14,15 Certain compounds derived from o-, m- and p-sulfobenzoic acid ligands and metallic ions are described in the literature, such as complexes with cobalt,^16,17 nickel,^18,19 zinc,^20,21 copper,^22–25 manganese^26–29 and silver.^30,31 These compounds are associated in various ways with metal ions connected through carboxylate groups or nitrogen ligands. However, in almost all of the compounds, the sulfonate groups are not coordinated directly to metal sites. Therefore, the coordination chemistry of compounds with sulfonate groups has been discarded because these groups are considered poor ligands.³²

p-Sulfobenzoic acid (psb) may be used as a precursor for different polymers because it exhibits different coordination sites with two different functional groups (carboxylate and sulfonate). The advantage of this ligand over carboxylate is that it allows an additional dimension for building networks and also a greater flexibility of modes combined with a nearly spherical shape.³³ However, most of these compounds described in the literature display a hydrated metal ion with the sulfonate group working as a non-coordinated ion or as a free sulfonate group in the lattice.^{18,25,34–36}

The formation of these compounds may be explained by the principle of hard and soft acids and bases (HSAB), where Lewis acids and bases are classified into three categories: hard, soft and borderline; thus, hard acids prefer to bind to hard bases and soft acids prefer to bind to soft bases.³⁷ Moreover, according to Klopman, solvation effects are also highly important;³⁸ therefore, in aqueous solution, there is a competition between sulfonate groups and water molecules over transition metal ions in the system. The covalent nature of transition metal ions appears to favor the hydration of metal ions over their interaction with sulfonate groups. This reduced hardness of the transition metal is responsible for the lack of chemical reactivity in aqueous solution.^39,40

There have been many efforts using different techniques to develop these high performance materials through crystallization by diffusion,^41,42 hydrothermal^43–45 and microwave hydrothermal^46–48 synthesis reactions, in which different solvents (water, methanol, ethanol, dimethylformamide) can be used to provide interactions between species, allowing a good environment for crystallization; however, to date, there have been no satisfactory results. The main methodology used in this work was crystallization of the crystals in gels used for the construction of polymers. This technique has been used in the literature for the crystallization of inorganic compounds and for the crystallization of macromolecules, where the crystallization agents most frequently used are agarose, polyacrylamide and silica.^49,50

In this context, we recently worked investigated the synthesis of coordination polymers containing sulfonate groups via crystallization in gels, using ethambutol hydrochloride as a new crystallization agent to encourage the construction of networks using transition metal ions and sulfonate group ligands.

Experimental section

Synthesis

[Zn(C₇H₅O₅S)₂(KC₇H₅O₅S)₂]·6H₂O: (Zn–psb). Two milliliters of ethanolic solution of zinc(II) nitrate hexahydrate (29.8 mg, 1 mmol) were added slowly dropwise to 5 mL of aqueous solution containing a monopotassium salt of 4-sulphobenzoate acid salt (24.2 mg, 1 mmol) and ethambutol hydrochloride (30.0 mg, 1.08 mmol). After approximately 6 months, single crystals were obtained by crystallization into the gel. However, only a few crystals were obtained with a suitable one used for the X-ray diffraction.

[Mn(C₇H₅O₅S)₂(KC₇H₅O₅S)₂]·6H₂O: (Mn–psb). The synthesis of Mn–psb was analogous to the synthesis of Zn–psb, except that instead of using an ethanolic solution of zinc(II) nitrate hexahydrate, the synthesis of Mn–psb used 2 mL of an ethanolic solution of manganese(II) nitrate tetrahydrate (29.8 mg, 1.19 mmol). After approximately 6 months, single crystals were obtained by crystallization into the gel. Similar to the Zn–psb compound, only a few suitable crystals were obtained and could be used for the X-ray diffraction studies.

Crystallographic determination

X-ray diffraction measurements for both compounds were carried out on an Oxford GEMINI A-Ultra CCD diffractometer with graphite monochromated MoKα (λ = 0.71073 Å) at room temperature. These structures were resolved by direct methods and then refined by a full-matrix least square refinement on F² using SHELXL-97.⁵¹ The figures were drawn by the ORTEP-3 for Windows,⁵² Mercury⁵³ and TOPOS4.0⁵⁴ programs. The maximum symmetry of embedding for the nets was given by the Systre⁵⁵ program.

Results and discussions

Structural description

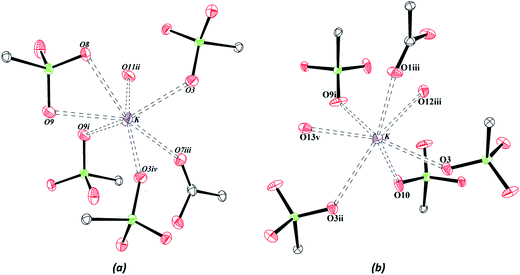
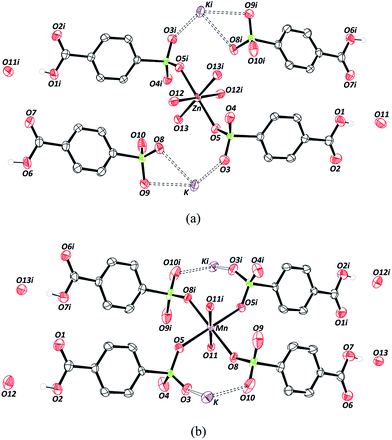
The crystallographic data on the compounds are displayed in Table 1. Both compounds crystallize in the triclinic crystal system and space group P1̄. The crystal structure of Zn–psb is displayed in Fig.　1(a), which shows that the ligand is coordinated to Zn and K atoms and presents the coordinated and free water molecules. The Zn–O distances are 2.02(2) Å [Zn–O12] and 2.14 (2) Å [Zn–O13] for water molecules and 2.12(2) Å [Zn–O5] for the ligand, whose O5 atom is derived from the sulfonate group. The Zn site adopts a slightly distorted octahedral geometry, and it is still possible to perceive that this atom is coordinated to the sulfonate group of the ligand by the coordination mode ημk.⁵⁶

Table 1 Crystallographic data for Zn–psb and Mn–psb

Compound	Zn–psb	Mn–psb
a R(Fo) = ∑||Fo| − |Fc||/∑|Fo|.b Rw(Fo^2) = [∑w(Fo^2 − Fc^2)^2/∑wFo^2]^1/2.
Empirical formula	ZnC28H32K2O26S4	MnC28H32K2O26S4
Formula weight (g mol^−1)	1056.35	1045.92
Crystal system	Triclinic	Triclinic
Space group	P1̄	P1̄
T (K)	293(2)	293(2)
a (Å)	8.080(4)	8.055(5)
b (Å)	11.385(6)	10.152(7)
c (Å)	12.282(6)	12.541(8)
α (∘)	97.402(4)	99.084(6)
β (∘)	106.530(4)	95.358(5)
γ (∘)	110.445(4)	106.090(6)
V (Å^3)	981.61(9)	962.78(11)
Z	1	1
MoKα (cm^−1)	0.71073	0.71073
D (g cm^−3)	1.787	1.804
R(Fo)^a	0.0441	0.0484
Rw(Fo^2)^b	0.0903	0.0862
S	1.136	1.079

---

Fig. 1 Crystal structures of (a) Zn–psb and (b) Mn–psb. Symmetry code: (i) (−x, −y, −z). Thermal ellipsoids at 50% probability.

There are two different types of psb ligand in the crystal structure, one that is coordinated to Zn and K atoms and another that interacts only with K ions, but in both cases, the carboxylic group remains in the acid form. The Mn–psb compound has the same quantity of water molecules in the crystal structure as the Zn–psb and ligand; however, the interactions are different. The Mn atom forms a slightly distorted octahedral geometry with the distance Mn–O11 of 2.17(2) Å of oxygen atoms from the water molecules and Mn–O5 and Mn–O8, with distances of 2.21 (3) Å and 2.17 (2) Å, respectively, from the oxygen atoms of the sulfonate groups, as shown in Fig.　1(b). The distances are similar in both compounds, but there is only one type of psb ligand in the Mn–psb structure with the coordination mode ημκ for the whole sulfonate groups.

The coordination between the metal and the oxygen atoms of the sulfonate groups can be elucidated by the presence of electrons in the d orbitals. The stability results from the increased number of d electrons that decrease with hardness in Lewis acids. Thus, Mn²⁺ ions are considered to be a hard acid, while Zn²⁺ ions have an intermediate hardness. When considering the effects of electronegativity, polarizability and the oxidation state for Lewis bases, the water molecule is classified as a harder base than the sulfonate group. It is known by HSAB that metal–water interactions are more stable than the other bonds considered. However, there is competition among water, the psb ligand, and ethambutol hydrochloride molecules during the crystallization process.

In very concentrated solutions of ethambutol hydrochloride, the ethambutol molecule may interact with water molecules and chloride ions to bind to soft metal ions such as Zn²⁺. The addition of the crystallization agent should increase the reactivity of metals in aqueous solution with ethambutol–water and chloride–ion interactions, and thus favor metal–sulfonate coordination.

The neutrality of the compounds is produced by protonation of all the carboxylate groups present in the structures, with average C–OH distances of 1.32(4) Å. The sulfonate groups are deprotonated with similar S–O bond distances, C–S–O angles and O–S–O angles in both compounds, with values of approximately 1.45(2) Å, 106.30(14)° and 112.32(12)°, respectively. The coordination environment of the potassium ions is shown in Fig.　2, and it has been observed that the K–O interactions are similar in the two structures, with average interaction distances of approximately 2.92(2) Å and 2.84(2) Å for Zn–psb and Mn–psb, respectively.

Fig. 2 Coordination environment of the potassium ion for (a) Zn–psb and (b) Mn–psb. Symmetry code: (i) (−x + 1, −y + 1, −z), (ii) (−x − 1, −y, −z − 1), (iii) (x − 1, −y + 1, −z), (iv) (−x, −y + 1, −z) for Zn–psb and (i) (−x + 2, −y, −z + 2), (ii) (−x + 1, −y, −z + 2), (iii) (−x + 1, −y, −z + 1), (v) (x − 1, y − 1, z − 1) for Mn–psb. Thermal ellipsoids at 25% probability.

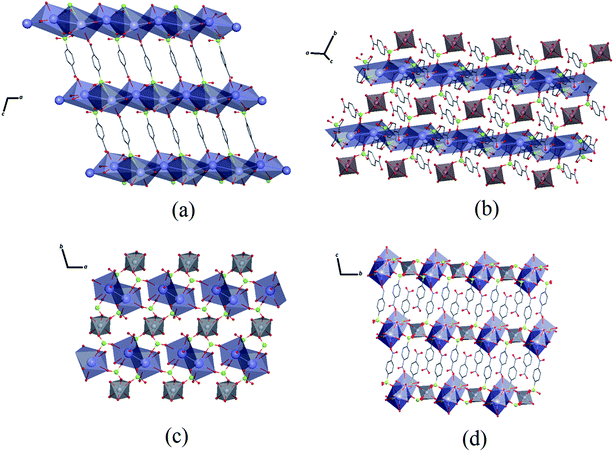
As seen in Fig.　3, the K–O interactions in Zn–psb give rise to a 2D network in the ac-plane that extends along the b-axis through Zn octahedral atoms coordinated with a psb ligand, forming a 3D polymeric net. Similarly, Mn–psb forms a 2D network in the ab-plane, and the 2D ladder is formed by K–O interactions and Mn octahedral atoms and is extended by bridge ligands to make a 3D polymeric net along the c-axis. The single-crystal X-ray diffraction analysis reveals that although the Zn–psb and Mn–psb structures show distinct environments for metal ion coordination, they have analogous crystallographic relationships, such as space group, unit cell and similar interactions, with a difference in unit cell volume of approximately 2%.

Fig. 3 (a) Extension of Zn–psb structure along the ac-plane and (b) along the b-axis. (c) Extension of Mn–psb structure along the ab-plane and (d) along the bc-plane. Color code: C: gray, O: red, S: green, K: lilac, Mn: light gray, Zn: brown.

Topological description

For rigorous structural analysis, it is important to use the topological description as a tool to clearly understand the extent of these compounds. The details of the crystal packing can be studied using the Topos4.0 package.⁵⁴ Crystal packing is the result of the sum of different interaction contributions, and in this case, hydrogen bonds have a secondary influence in building the compounds. A topological study of the packing modes of hydrogen bonds is difficult in compounds, because the patterns of interactions are dispersed in 3D space. However, the presence of water molecules in the compounds leads to the formation of a complex system of hydrogen bonds. Pertinent parameters, such as the O⋯O distances for carboxylic, sulfonate and water oxygen atoms are given in Table 2. In both compounds, the distances for classical hydrogen bonding are classified as moderate to weak.

Table 2 Parameters for hydrogen bonds for Zn–psb and Mn–psb structures^a

D	H	A	D–H	H⋯A	D⋯A	D–H⋯A	Ω(A)/Å^2	Ω(H⋯A)/%
a Symmetry code: (i) (−1 − x, −y, −1 − z); (ii) (1 − x, 1 − y, 1 − z); (iii) (1 + x, y, 1 + z); (iv) (−x, −y, −z), (v) (2 − x, 1 − y, 2 − z); (vi) (1 + x, y, z); (vii) (x, y, −1 + z), (viii) (−1 + x, y, −1 + x), (ix) (−1 + x, y, −1 + x), (x) (1 − x, 1 − y, 1 − z).
Zn–psb
O1	H1C	O11^i	0.6900	1.9500	2.625(4)	168.00	23.94	22.18
O6	H6C	O4^ii	0.8600	2.1700	2.948(3)	150.00	29.11	16.80
O11	H11B	O13	0.8400	2.1300	2.880(3)	150.00	19.81	18.98
O12	H12A	O2^iii	0.8500	1.8800	2.727(3)	170.00	34.43	23.50
O12	H12B	O8	0.8100	1.9600	2.744(3)	162.00	36.02	18.78
O13	H13A	O4^iv	0.8400	2.1300	2.879(3)	149.00	29.11	15.80
O13	H13B	O10	0.8400	1.9000	2.733(4)	171.00	33.86	23.00
Mn–psb
O2	H2C	O12	0.7900	1.8600	2.650(4)	176.00	22.36	23.57
O7	H7C	O13^v	0.8300	1.8000	2.618(3)	167.00	21.61	20.96
O11	H11A	O4^vi	0.8300	2.0100	2.784(4)	155.00	31.09	19.17
O11	H11B	O6^vii	0.8300	1.9000	2.732(4)	179.00	33.49	21.53
O12	H12A	O10^viii	0.8400	2.3100	3.130(5)	166.00	34.50	15.04
O12	H12B	O11^ix	0.8100	2.1100	2.887(4)	160.00	19.44	15.12
O13	H13A	O8^vii	0.8400	2.1200	2.942(4)	168.00	31.56	17.81
O13	H13B	O4^x	0.8300	2.2600	2.973(4)	145.00	31.19	15.68

---

The geometric factors derived from the Voronoi–Dirichlet Polyhedral (VDP) were also considered (Table 2). Fig.　4 shows the VDP of certain hydrogen atoms in the Zn–psb and Mn–psb structures. The method considers the whole surroundings of the atoms, where the size of the face of the convex polyhedron formed represents the solid angle of the face (Ω) and is a definite percentage of the sum of solid angles of all other faces that can represent different types of interactions, such as hydrogen bonds [Ω(H⋯A)].⁵⁷ These results show that when the distances H⋯A begin to decrease, the percentage of solid angles increases, and more strong hydrogen bonds are found.

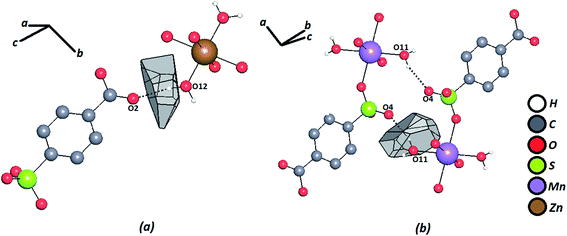Fig. 4 Voronoi–Dirichlet polyhedron of a hydrogen atom for (a) Zn–psb and (b) Mn–psb. Hydrogen bonds are shown by dash-and-dotted lines.

Certainly, their observation is associated directly with a contribution to the construction of the VDP faces. For the Zn–psb compound, the hydrogen bond network extends in 3D space for infinite chains made by interactions of the oxygen atoms of the carboxyl groups (O1, O2), water molecules (O11, O12, O13) and sulfonate groups (O4, O10 and O4, O6), as shown in Fig.　5. Similar interactions are found in the Mn–psb compound; however, the complex packing of hydrogen bonds among these groups can be explored using graph theory, such as with graph-set assignments.⁵⁸ In particular, Mn–psb possesses hydrogen bond motifs involving oxygen atoms of carboxyl groups (O6), water molecules (O13, O11) and sulfonate groups (O4) that form a highly extensive ring motif specified as R⁴₄(70), as illustrated in Fig.　6. To build the simplified model for other interactions, a set of atoms associated with the actual connection of the structure was considered, respecting the nature and extent of the connections into the crystal structures. For example, in the Zn–psb structure, the ligand center includes a vertex 3-connected to another vertex by 8-connected potassium ions, as illustrated in Fig.　7.

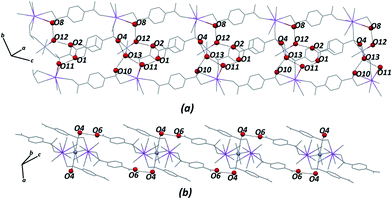Fig. 5 Extensions of the hydrogen bond network in 3D space for the Zn–psb structure. Some atoms are not shown for clarity.

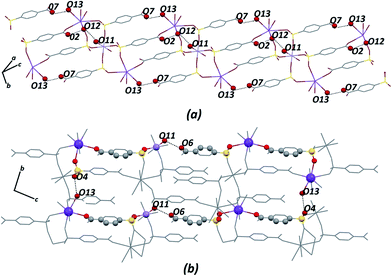Fig. 6 For Mn–psb structure, (a) extension of the hydrogen bond network in 3D space and (b) graph-set for the hydrogen bond motif selected. Some atoms are not shown for clarity.

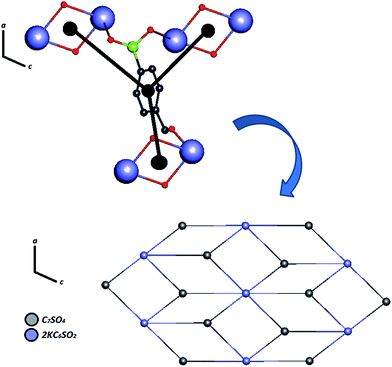Fig. 7 Simplified model of Zn–psb for building a binodal (3,6)-coordinated ladder along the ac-plane.

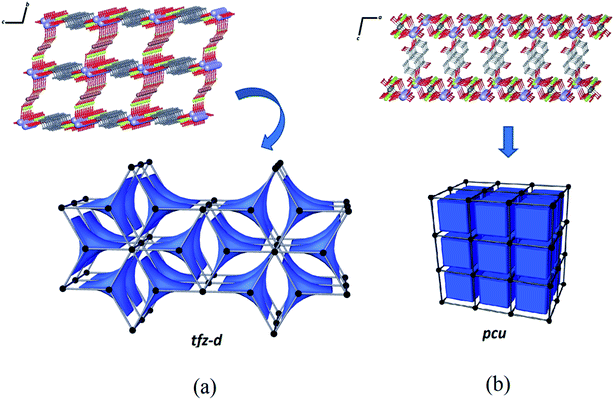
The structure of Zn–psb consists of a binodal (3,8)-connected system and can be described with a point symbol (4³) by the vertex formed for the ligand and (4⁶.6¹⁸.8⁴) for the vertex constructed using the potassium ions. This network is deposited in RCSR⁵⁹ as a net of type tfz-d with hexagonal symmetry P6/mmm with two different tiles of transitivity [2222] and signature 3[4².6²] + 2[6³], as illustrated by Fig.　8(a). Despite the structural similarities of the compounds, a simple modification of the metal ion in the reaction leads to a tendency toward a different network with different topological properties. The Mn–psb structure leads to the formation of a single regular pcu type network with Pm3̄m symmetry, where one type of tile is observed in the cubic form with transitivity [1111] and signature [4⁶], as shown in Fig.　8(b). This evidence may be used to predict possible structural modifications that may cause the growth of interpenetrated nets.

Fig. 8 (a) Part of tfz-d net with P6/mmm symmetry derived from the Zn–psb structure. One of the [6³] tiles for the net is shown in blue. (b) Regular pcu net derived from the Mn–psb structure. The symmetry of the tiling is Pm3̄m, which has one type of tile displayed in blue.

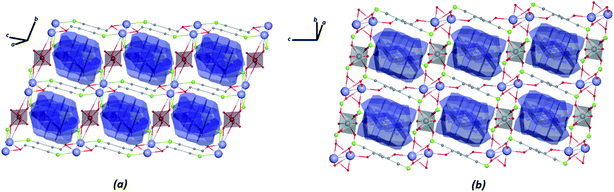
The construction of the tiles of networks for structures in combination with the VDP method was used to investigate the system cavities in the crystal structures. As shown in Fig.　9, the systems of cavities in the network described by tiles are blocked for the ligands facing the direction of potential voids, with a volume of approximately 279.54 ų and 265.17 ų, respectively, for Zn–psb and Mn–psb.

Fig. 9 VDP fragments of the crystal structures of (a) Zn–psb and (b) Mn–psb.

Conclusion

In spite of the similarities between the structural parameters of the compounds Zn–psb and Mn–psb, it was observed that the modification of the metal in the synthesis process leads to the construction of two different networks (tdz-d and pcu, respectively), with divergent topological properties, where the system of cavities found are blocked by the presence of the psb ligand in both compounds. The coordination of the sulfonate group with the transition metal is usually measured as weakly interacting and makes an aqua complex. However, when crystallization in the gel method was employed, a major interaction between the transition metal and the sulfonate group was observed that may be explained by the fact that the presence of ethambutol hydrochloride provides a lower affinity of metal with water molecules, preventing the formation of aqua ligands and thereby giving greater accessibility of the sulfonate group to the metal. However, the results are satisfactory for obtaining polymeric crystal structures involving the sulfonate group and transition metals with similar structures and different topological proprieties. It has been observed that the use of ethambutol hydrochloride as a new crystallization gel increases the crystallization time of small molecules, as demonstrated by the low yields of these materials. Other crystallization agents with densities higher than that of water, such as glycerin and ethylene glycol, have been tried by our research group to increase the yields of these crystals. However, they reduce sedimentation and nucleation, proving an obstacle to the formation of precipitate or crystals from the solution. Future efforts should be directed toward the advancement of methods to produce crystals using sulfonate groups and transition metal ions.

Acknowledgements

This research used resources of the Coordination of Improvement of Higher Education Personnel (CAPES), the Foundation for Research Support of Minas Gerais (FAPEMIG) and the National Council for Scientific and Technological Development (CNPq). The authors thank the Crystallography Laboratory (LabCri – UFMG) for providing facilities for the measurement of X-ray diffraction.

References

1. F. D. Rochon and G. Massarweh, Inorg. Chim. Acta, 2001, 314, 163–171.
2. W. Zhang, S. Bruda, C. P. Landee, J. L. Parent and M. M. Turnbull, Inorg. Chim. Acta, 2003, 342, 193–201.
3. P.-Z. Li, X.-M. Lu and X.-Z. Yang, Inorg. Chim. Acta, 2008, 361, 293–298.
4. H.-T. Chung, H.-L. Tsai, E.-C. Yang, P.-H. Chien, C.-C. Peng, Y.-C. Huang and Y.-H. Liu, Eur. J. Inorg. Chem., 2009, 3661–3666.
5. X. Xinxin, L. Xiaoxia, S. Xiaoguang and W. Enbo, J. Coord. Chem., 2010, 63, 3060–3070.
6. M. Anbia, V. Hoseini and S. Sheykhi, J. Ind. Eng. Chem., 2012, 18, 1149–1152.
7. Z. Bao, L. Yu, Q. Ren, X. Lu and S. Deng, J. Colloid Interface Sci., 2011, 353, 549–556.
8. J.-R. Li, R. J. Kuppler and H.-C. Zhou, Chem. Soc. Rev., 2009, 38, 1477–1504.
9. D. Farrusseng, S. Aguado and C. Pinel, Angew. Chem., Int. Ed., 2009, 48, 7502–7513.
10. U. Ravon, M. E. Domine, C. Gaudillere, A. Desmartin-Chomel and D. Farrusseng, New J. Chem., 2008, 32, 937–940.
11. M. Riou-Cavellec, C. Albinet, C. Livage, N. Guillou, M. Noguès, J. M. Grenèche and G. Férey, Solid State Sci., 2002, 4, 267–270.
12. J.-Q. Liu, J. Wu, Y.-Y. Wang, J.-T. Lin and H. Sakiyama, CrystEngComm, 2014, 16, 3103–3112.
13. J.-W. Zhang, W. Zhao, Q.-L. Lu, J. Luan, Y. Qu and X.-L. Wang, J. Solid State Chem., 2014, 212, 151–158.
14. P. L. Feng, J. V. Branson, K. Hattar, G. Vizkelethy, M. D. Allendorf and F. Patrick Doty, Nucl. Instrum. Methods Phys. Res., Sect. A, 2011, 652, 295–298.
15. R. C. Huxford, J. Della Rocca and W. Lin, Curr. Opin. Chem. Biol., 2010, 14, 262–268.
16. Y. Bu, F. Jiang, S. Zhang, J. Ma, X. Li and M. Hong, CrystEngComm, 2011, 13, 6323–6326.
17. H.-P. Xiao, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, m95–m97.
18. L. H. Chagas, S. B. P. De Farias, A. A. Leitão, R. Diniz, S. S. X. Chiaro, N. L. Speziali, H. A. De Abreu and W. N. Mussel, Quim. Nova, 2012, 35.
19. X.-H. Miao and L.-G. Zhu, CrystEngComm, 2009, 11, 1112–1117.
20. H.-P. Xiao, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, m1611–m1612.
21. H. Wang, L.-H. Huo, Z.-P. Deng, H. Zhao and S. Gao, CrystEngComm, 2012, 14, 3501–3508.
22. W.-B. Zhang, J.-G. Wang, H.-X. Chen and H.-P. Xiao, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61, m2559–m2560.
23. A.-Y. Wang, J. Wang, S. Aghabeygi, J.-G. Wang, H.-P. Xiao and A. Mosali, J. Inorg. Organomet. Polym. Mater., 2011, 21, 700–705.
24. X.-H. Miao and L.-G. Zhu, J. Mol. Struct., 2008, 877, 123–131.
25. L.-P. Zhang and L.-G. Zhu, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61, m1264–m1265.
26. H.-P. Xiao, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61, m942–m944.
27. T.-J. Yang, H.-P. Xiao and L.-G. Zhu, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, m1671–m1672.
28. X.-H. Miao and L.-G. Zhu, New J. Chem., 2010, 34, 2403–2414.
29. C.-S. Liu, J.-R. Li, C.-Y. Li, J.-J. Wang and X.-H. Bu, Inorg. Chim. Acta, 2007, 360, 2532–2540.
30. X.-F. Zheng and L.-G. Zhu, Cryst. Growth Des., 2009, 9, 4407–4414.
31. X.-F. Zheng and L.-G. Zhu, Inorg. Chim. Acta, 2011, 365, 419–429.
32. A. P. Côté and G. K. H. Shimizu, Coord. Chem. Rev., 2003, 245, 49–64.
33. S. K. Mäkinen, N. J. Melcer, M. Parvez and G. K. H. Shimizu, Chem. –Eur. J., 2001, 7, 5176–5182.
34. C. Wagner and K. Merzweiler, Z. Anorg. Allg. Chem., 2010, 636, 557–561.
35. W. Xiong, Y. Su, Z. Zhang, Z. Chen, F. Liang and L. Wang, J. Chem. Crystallogr., 2011, 41, 1510–1514.
36. L.-P. Zhang and L.-G. Zhu, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61, m1768–m1770.
37. R. G. Pearson, J. Chem. Educ., 1968, 45, 581.
38. G. Klopman, J. Am. Chem. Soc., 1968, 90, 223–234.
39. R. G. Pearson, Inorg. Chem., 1988, 27, 734–740.
40. R. G. Pearson, J. Chem. Educ., 1968, 45, 643.
41. O. Fabelo, L. Canadillas-Delgado, J. Pasan, C. Ruiz-Perez and M. Julve, CrystEngComm, 2006, 8, 338–345.
42. V. S. Dhanya, M. R. Sudarsanakumar, S. Suma, S. W. Ng, M. S. Augustine and S. M. Roy, Inorg. Chem. Commun., 2013, 35, 140–143.
43. G.-L. Li, W.-D. Yin, G.-Z. Liu, L.-F. Ma, L.-L. Huang, L. Li and L.-Y. Wang, Inorg. Chem. Commun., 2014, 43, 165–168.
44. X.-H. Chang, J.-H. Qin, L.-F. Ma and L.-Y. Wang, J. Solid State Chem., 2014, 212, 121–127.
45. M.-L. Han, S.-C. Wang and D.-F. Feng, Cryst. Res. Technol., 2014, 49, 276–282.
46. P. Amo-Ochoa, G. Givaja, P. J. S. Miguel, O. Castillo and F. Zamora, Inorg. Chem. Commun., 2007, 10, 921–924.
47. J.-S. Choi, W.-J. Son, J. Kim and W.-S. Ahn, Microporous Mesoporous Mater., 2008, 116, 727–731.
48. J. Klinowski, F. A. Almeida Paz, P. Silva and J. Rocha, Dalton Trans., 2011, 321–330.
49. A. Moreno, E. Saridakis and N. E. Chayen, J. Appl. Crystallogr., 2002, 35, 140–142.
50. H. Sugimoto, K. Daimatsu, E. Nakanishi, Y. Ogasawara, T. Yasumura and K. Inomata, Polymer, 2006, 47, 3754–3759.
51. G. M. Sheldrick, SHELXL-97-A Program for Crystal Structure Refinement, University of Goettingen, Germany, 1997.
52. L. Farrugia, J. Appl. Crystallogr., 1997, 30, 565.
53. C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr., 2006, 39, 453–457.
54. Topos4.0, 2012.
55. O. Delgado-Friedrichs and M. O'Keeffe, Acta Crystallogr., Sect. A: Found. Crystallogr., 2003, 59, 351–360.
56. T. Kurc, J. Janczak, J. Hoffmann and V. Videnova-Adrabinska, Cryst. Growth Des., 2012, 12, 2613–2624.
57. I. A. Baburin, V. A. Blatov, L. Carlucci, G. Ciani and D. M. Proserpio, Cryst. Growth Des., 2008, 8, 519–539.
58. M. C. Etter, J. C. MacDonald and J. Bernstein, Acta Crystallogr., Sect. B: Struct. Sci., 1990, 46, 256–262.
59. M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782–1789.

---

Footnote

† CCDC 1004574 and 1004580. For crystallographic data in CIF or other electronic format see DOI: 10.1039/c4ra07629j

---