Synthesis, growth mechanism and elastic properties of SiC@SiO₂ coaxial nanospring

Abstract

Herein, a novel coaxial nanospring composed of a helical SiC core and a uniform amorphous SiO₂ sheath (SiC@SiO₂) has been synthesized via a template/catalyst-free chemical vapor reaction (CVR) approach. An atomic layer dislocation stacking growth model is firstly established for explaining the formation process of the nanospring, which offers a valuable model and an effective clue for understanding the growth of other nonlinear nanostructures. The elastic properties of the products have been investigated by calculating the corresponding spring constant of the SiC@SiO₂ coaxial nanospring with a dynamic radius, which makes it a promising candidate for nanomechanical devices, self-sensing resonators and nanoscale elastic energy storage.

---

Introduction

After two decades of fruitful research and development, it has been adequately demonstrated that the superior performance of nanomaterials is closely correlated with their peculiar morphologies.^1–3 Owing to the distinctive structures, one-dimensional (1D) linear nanomaterials, such as nanowires,⁴ nanorods,⁵ nanocables,⁶ nanotubes,⁷ nanobelts,⁸ nanoneedles,⁹ have aroused enormous interest as building blocks and functional components in nanoelectronics, nanophotonics and nanomechanics devices.^10,11 However, scientists never cease to pursue novel morphology, and a considerable amount of effort is spent on the synthesis of 1D nonlinear nanostructures.¹²

Helical nanostructures (nanosprings) are probably the most amusing 1D morphology with their remarkable periodic and peculiar chirality.¹³ Since the first observation of the ZnO nanospring,¹⁴ people have immediately expressed profound curiosity and research interest in exploring whether this morphology can be extended to other materials. Soon afterwards, a number of nanomaterials, such as carbon nanotubes (CNTs),¹⁵ silicon/silicon dioxide (Si–SiO₂),¹⁶ zinc oxide (ZnO)¹⁷ and InGaAs/GaAs¹⁸ helical nanostructure have been consecutively fabricated.

Properties may be endowed for these helical nanomaterials. Attention is instinctively payed on the elastic behavior because of the apparent similarities between helical nanostructure and conventional coil spring in our daily life. Cao et al. have reported that the spring constant of the Si₃N₄ microcoil showed changeless with increasing cyclic loadings, exhibiting the stability of their tensile properties, furthermore, the relationship between the tensile strength and the diameter of coil whisker has also been deduced.¹⁹ Chen et al. apply atomic force microscopy (AFM) to exploit a helical amorphous CNT with a spring constant K of 0.12 N m⁻¹ in a low strain region.²⁰ Afterwards, the mechanical property of SiO₂ nanospring is also studied, which demonstrates that a bent helical structure can contract and expand under electron beam heating.²¹ The super-elasticity and nanoscale fracture behavior of the ZnO nanospring is reported by Wang and his co-workers, and the corresponding spring constant can be increased (theoretically) continuously for up to 300–800%.²² The internal structure and the superelastic mechanism of Si₃N₄ microsprings are proposed using Raman spectroscopy upon stretching gradually.²³ First-principle has been used to investigate the elastic constants of zinc-blende GaN by Usman et al., furthermore, the calculated elastic constants of wurtzite GaN have been used to calculate the shear wave speeds in the [100] and [001] planes.^24,25

Recently, depending on their excellent mechanical strength,²⁶ high-thermal conductivity²⁷ and promising application in high-temperature semiconductors²⁸ and electron field-emitting devices,^29–31 silicon carbide (SiC) nanostructures have aroused much attention. Zhang et al. have reported the synthesis of the helical SiC/SiO₂ coaxial nanostructure via a chemical vapor deposition (CVD) method, and a screw-dislocation-driven growth mechanism is successfully proposed to explain the formation of the products.³² Using the same method, amorphous helical SiO₂ nanosprings were also synthesized by them. Contraction and expansion behaviors of the helical SiO₂ nanosprings were directly observed, suggesting their wide potential applications in various fields.²¹ Scientists have also obtained amorphous silicon carbide nanosprings, as well as biphase helical nanowires according to vapor–liquid–solid mechanism, furthermore, a modified contact angle anisotropy model has been proposed to explain the formation of the biphase helical nanowires.³³ A model for growing helical nanostructure motivated by both energy and entropic principles have been reported by Bandaru et al.³⁴ Although some valuable data have been obtained by scientists, however, there is seldom reference about the elastic property of helical SiC nanostructure, especially SiC@SiO₂ coaxial nanospring.

Herein, SiC@SiO₂ coaxial nanospring has been synthesized via template/catalyst-free CVR method. The related formation mechanism is firstly established via dislocation stacking growth model and force analysis of the atomic layer. This model also offers a valuable model and effective clue for understanding the growth process of other nonlinear nanostructures. Furthermore, the elastic property of the SiC@SiO₂ coaxial nanospring has been evaluated by its spring constant of 6.37 N m⁻¹ under unstressed state. Not only the value implies that the coaxial nanospring a potential candidate for nanomechanics device, self-sensing resonators and nanoscale elastic energy storage, but also the spring constant calculation in this manuscript provides a facile way to evaluate the elastic property of the coaxial nanospring.

Experimental section

Synthesis of the helical SiC@SiO₂ coaxial nanospring

In order to reduce the reaction temperature, the Si–SiO₂ raw materials was pretreated using ball grinding mill, the TEM image and corresponding XRD pattern of milled Si–SiO₂ mixture powders see Fig. S1 and S2 in ESI.† Milled Si–SiO₂ mixture powder (molar ratio Si : SiO₂ = 1.5 : 1) and high purity CH₄ were used as raw materials, carbon wafer was used as substrate, and vertical hot zone furnace was employed as experimental equipment. Initially, the substrate, carbon cloth and milled Si–SiO₂ powder were orderly placed in a homemade graphite reaction chamber. Secondly, the chamber was totally placed into the vertical furnace, before heating the furnace was purged 2–3 times with high-purity Ar by using a rotary vacuum pump to reduce the concentration of oxygen to a negligible level. Thirdly, the temperature was increased to 1250 °C from room temperature at a mean rate of 800 °C h⁻¹ and maintained the peak temperature for 10–15 min, during the peak temperature, a steady flow of CH₄ at 0.04–0.08 sccm from the bottom of the furnace was introduced into the reaction system, meanwhile the atmospheric pressure was consecutively increased from 200 to 700 torr which was controlled by aerating the Ar into the furnace. Finally, the CH₄ and Ar valves were closed, and the furnace was cooled to room temperature.

Characterization

A layer of blue products were obtained on the carbon substrate after the CVR process. The micro-morphology and chemical composition were characterized by using a JEOL JSM-6 field emission scanning electron microscope (FE-SEM) equipped with energy-dispersive X-ray spectroscope (EDX) equipment. Further detailed structural information of the obtained nanostructures was acquired by using a JEM-2000EX transmission electron microscopy (TEM), JEOL-2010 high-resolution transmission electron microscopy (HR-TEM) and the corresponding selected area electron diffraction (SAED). The X-ray diffraction (XRD) pattern of the gained nanostructures was recorded by using a Rigaku D/max-2400 X-ray diffractometer at room temperature.

Results and discussion

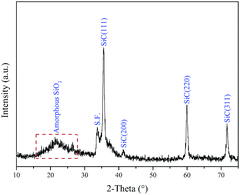
Fig. 1 exhibits the XRD pattern of coaxial nanospring deposited on the substrate. It can be clearly observed that the major diffraction peaks are in good agreement with the known for SiC (JCPDS Card. no. 29-1129), which can be assigned to the (111), (200), (220), (311) reflections of cubic structure, suggesting that cubic SiC is the only crystalline phase besides the graphite substrate. Furthermore, the low intensity peak marked with S.F. should be attributed to the stacking faults in SiC core nanosprings. As shown in Fig. 1, the broad XRD peak at low diffraction angle (∼20°) is attributed to the amorphous SiO₂ coatings around SiC nanospring.

Fig. 1 Representative XRD patterns of as-obtained products directly grown on graphite substrate.

Fig. 2a shows that helical nanosprings of several microns in length randomly distribute on the substrate surface. It can be clearly found that most of the nanosprings display helical or quasi-helical structure without the assistance of the catalyst. Furthermore, the growth direction of the isolated nanospring abides by the left handed or right handed helix law, respectively. According to the statistics from dozens of helical nanostructures, the corresponding size distribution histograms of screw diameter (green) and helical periodicity (red) are also exhibited in the inset of Fig. 2a, respectively. It can be observed that representative size of the screw diameter distributes around 150 nm, and the absolute high proportion size of the helical periodicity is approximately 100 nm, respectively. Fig. 2b indicates the partial enlarged area of an isolated SiC@SiO₂ coaxial nanospring, which displays right-handed helical profile with smooth surface. The inset of Fig. 2a depicts a typical EDS spectrum recorded from the isolated nanospring, which displays that the product contains Si, C and O elements. According to our previous research,^35,36 the O is mainly from the amorphous oxidation layer around the SiC core, and it can be confirmed that the nanostructure is composed of crystalline SiC core and amorphous SiO₂ shell.

Fig. 2 (a) FE-SEM image of as-obtained helical and quasi-helical nanostructures, the inset in (a) is the size distribution of the screw diameter (green) and pitch distance (red). (b) Typical high-magnification FE-SEM image of single SiC@SiO₂ nanostructures, the insert is corresponding EDS pattern.

Fig. 3 shows the TEM, HRTEM images and SAED pattern of a representative isolated SiC@SiO₂ coaxial nanosprings. The nanospring with well helical-shaped outline and different phase contrast is composed of crystalline SiC core with diameter of 25 nm and amorphous SiO₂ coating with thickness of 10 nm. As marked in Fig. 3a, the corresponding screw diameter is about 150 nm, and the screw pitch between two adjacent periodic helical rings is approximately 100 nm. The corresponding inset is the obtained SAED pattern, a series of bright spots and amorphous halo-like trait can be indexed to the cubic SiC and SiO₂ coating. Fig. 3b and c display the HRTEM images recorded from the corner areas of the both sides marked 1 and 2 in Fig. 3a, respectively. It can be clearly observed that the thickness of the amorphous coatings is approximately 10 nm, and the inter-planar spacing of the single-crystalline core is 0.25 nm, which is consistent with the value of the SiC [111] lattice direction. In addition, it is noteworthy that the growth direction keeps invariable in Fig. 3b and c, which is crucial for understanding the growth process of the coaxial nanospring.

Fig. 3 (a) TEM image of single helical nanowire with screw diameter about 150 nm. High resolution TEM images (b and c) of the nanowire taken from corresponding area in (a) labeled 1 and 2. The insets in a is the SAED pattern.

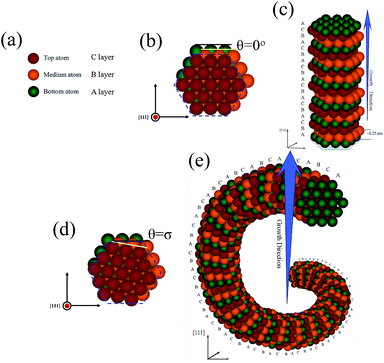
In order to intuitively analyze the formation mechanism, a growth model of SiC@SiO₂ nanospring controlled by the atomic layer dislocations stacking theory is proposed as following: it is well-known that the stacking arrangement in cubic SiC structure is ABC,³⁷ herein, bottom, medium and top atom in different colors can be regarded as A (green), B (yellow) and C (red) atomic layer, as shown in Fig. 4a. According to the crystallography, the SiC crystal nucleus deposits along the [111] growth direction with 0.25 nm inter-planar spacing because having the lowest nucleation energy. For ideal nucleus of 1D SiC linear nanostructures, every upper atom in (111) close-packed plane is positioned in the centers of triangular depressions formed by three adjacent lower atoms, as indicated in Fig. 4b. The fresh atomic layer will deposit at the surface of the formed ideal nucleus, with prolonging the reaction time, which yields a 1D wire-like SiC nanostructures grown along the [111] orientation with ABCABC… stacking sequence, as shown in Fig. 4c. For SiC@SiO₂ nanospring, without the assistance of any catalyst and template, the deposition position of the initial nucleus can not be effectively limited to the centers of triangular depressions on the (111) lattice plane as well as SiC linear nanostructures, moreover, the deposition velocity of the atoms in same layer may also be diverse under the preparation condition, which may generate distortion energy and make the dislocation stacking more likely to occur between two adjacent atomic layers. As shown in Fig. 4d, the later formed atomic layer in nanospring nucleus has deviated from its original centers of triangular depressions (blue dashed line) by σ degree (the angular separation is defined as θ). Although stacking along the [111] direction for coaxial nanospring, however, it is not the best and lowest energy position for most of the atoms on the (111) lattice plane, which may generate distortion energy. Subsequently, the fresh deposited atom layer will continuously deposit on the obtained nucleus surface and form fresh dislocation stacking on (111) lattice plane for decreasing the total distortion energy, the corresponding atomic structure model of the SiC nanospring along [111] growth direction are shown in Fig. 4e. With prolonging the reaction time, the SiC core nanospring can be fabricated by the continuously vapor–solid (VS) mechanism.^38–40 The force analysis of the atomic layer was also carried out (see Fig. S3 in ESI†), which confirms the rationality of the proposed model. As illustrated in our previous paper,³⁶ the residual SiO vapor is oxidized to amorphous SiO₂ coating distributed evenly around the SiC nanospring with the thickness of 10 nm when the C atoms are exhausted, which may also play a significant role in stabilizing the helical SiC core. Finally, the SiC@SiO₂ coaxial nanospring can be collected after the reaction.

Fig. 4 (a) Si atoms at different stacking layers (b) Ideal stacking arrangement of the SiC nucleus (corresponding C atoms is completely omitted) (c) Atomic stacking model of as-obtained linear SiC nanostructure (d) Atomic layer dislocation stacking nucleus of the SiC core nanospring (e) Atomic stacking model of one geometric symmetry cycle of the SiC core nanospring.

As an important index for evaluating the elastic property of the helical nanostructure, the spring constant of the SiC@SiO₂ coaxial nanospring is also of concern to us. In order to deduce the formula of the spring constant of the SiC@SiO₂ coaxial nanospring, the dimensions gathered from the unstressed state nanospring (as shown in Fig. 3a) is taken as an example, and a reasonable model is firstly built as shown in Fig. 5a. According to Hook's law, the spring constant of parallel spring system composed of different materials is equal to the numerical superposition of the spring constant of single component. As illustrated in Fig. 5a, structurally, the SiC@SiO₂ coaxial nanospring can be regarded as a parallel complex system composed of single SiC core nanospring and SiO₂ coating nanospring. The spring constant of the SiC@SiO₂ coaxial nanospring (K_SiC@SiO2) is equal to the aggregation of the corresponding value of single SiC nanospring core (K_SiC) and SiO₂ coating (K_SiO2(h)).

Fig. 5 (a) Structural separation of the SiC@SiO₂ coaxial nanospring (b) The function of the spring constant depends on dynamic radius, in which the spring constant variation of SiO₂ coating and SiC core are also displayed, respectively, the inset is the partial enlarged drawing.

On the basis of the virtual work principle, classical elasticity theory and some reasonable assumption (see Fig. S4 in ESI†), series parameters of the SiC@SiO₂ coaxial nanospring have been used for numerical analysis on the radius dependence of the spring constant upon extension or compression. The corresponding curve graphs with spring constant as ordinate and dynamic radius as abscissas are shown in Fig. 5b. The desired spring constant of SiO₂ hollow nanospring (K_SiO2(h), pink solid line in Fig. 5b) and SiC@SiO₂ coaxial nanospring (K_SiC@SiO2, green solid line in Fig. 5b) can be drawn by the simple calculations (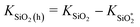, K_SiC@SiO2 = K_SiC + K_SiO2(h)). It is clearly seen that the original spring constants of the SiC@SiO₂ coaxial nanospring, SiC nanowire core and SiO₂ coating under strain free condition are 6.37 N m⁻¹, 2.65 N m⁻¹ and 3.72 N m⁻¹, respectively. Comparing with the recently reported references,^20,22,41 this values show larger load-bearing ability. Furthermore, both the absolute value and variation tendency (slope of the tangent to the spring constant curve) of the spring constants for SiC@SiO₂ coaxial nanospring are larger than other components (SiC core, SiO₂ coating and SiO₂ solid nanospring) at the same radius, showing peculiar elastic property which can not be matched by isolated core or coating nanostructures. The high spring constant of the SiC@SiO₂ coaxial nanospring makes it a potential structure for nanomechanics device, self-sensing resonators and nanoscale elastic energy storage.

Conclusions

In summary, a novel SiC@SiO₂ coaxial nanospring have been obtained via simple CVR approach under template/catalyst-free condition. Characterizations results show that the representational nanostructures are composed of crystalline SiC helical nanowires with diameter of approximately 25 nm and uniform amorphous SiO₂ wrapping layers with thickness of 10 nm. An atomic layer dislocation stacking growth model along [111] growth direction has been firstly illustrated, which successfully explains the formation process of the coaxial nanospring. Moreover, the peculiar elastic property of the SiC@SiO₂ coaxial nanospring is also evaluated by calculating the corresponding spring constant, showing 6.37 N m⁻¹ under unstressed state, which is larger than the value of single SiC core or SiO₂ coating. The interesting performance makes it a potential structure for nanomechanics device, self-sensing resonators and nanoscale elastic energy storage.

Acknowledgements

The work reported here was supported by the National Natural Science Foundation of China under Grant no. 51272117, 51172115, the Natural Science Foundation of Shandong Province under Grant no. ZR2011EMZ001, ZR2011EMQ011, ZR2013EMQ006, the Research Award Fund for Outstanding Young Scientists of Shandong Province Grant no. BS2013CL040, the Specialized Research Fund for the Doctoral Program of Higher Education of China under Grant no. 20123719110003 and the Tackling Key Program of Science and Technology in Shandong Province under Grant no. 2012GGX10218, the Application Foundation Research Program of Qingdao under Grant no. 13-1-4-117-jch. We express our grateful thanks to them for their financial support.

References

1. Y. Wang, H. D. Tran, L. Liao, X. F. Duan and R. B. Kaner, J. Am. Chem. Soc., 2010, 132, 10365.
2. S. K. Kim, R. W. Day, J. F. Cahoon, T. J. Kempa, K. D. Song, H. G. Park and C. M. Lieber, Nano Lett., 2012, 12, 4971.
3. H. Zheng, J. Z. Ou, M. S. Strano, R. B. Kaner, A. Mitchell and K. Kalantar-zadeh, Adv. Funct. Mater., 2011, 21, 2175.
4. H. Jiang, T. Zhao, J. Ma, C. Y. Yan and C. Z. Li, Chem. Commun., 2011, 47, 1264.
5. R. Z. Li, X. Ren, F. Zhang, C. Du and J. P. Liu, Chem. Commun., 2012, 48, 5010.
6. F. F. Cao, J. W. Deng, S. Xin, H. X. Ji, O. G. Schmidt, L. J. Wan and Y. G. Guo, Adv. Mater., 2011, 23, 4415.
7. H. Mirabolghasemi, N. Liu, K. Y. Lee and P. Schmuki, Chem. Commun., 2013, 49, 2067.
8. Z. X. Yang, W. Zhong, Y. Deng, C. T. Au and Y. W. Du, Cryst. Growth Des., 2011, 11, 2172.
9. S. Vallejos, T. Stoycheva, P. Umek, C. Navio, R. Snyder, C. Bittencourt, E. Llobet, C. Blackman, S. Moniz and X. Correig, Chem. Commun., 2011, 47, 565.
10. W. Zhou, X. Dai, T. M. Fu, C. Xie, J. Liu and C. M. Lieber, Nano Lett., 2014, 14, 1614.
11. R. Silva, Angew. Chem., Int. Ed., 2012, 124, 7283.
12. L. Colombo and S. Giordano, Rep. Prog. Phys., 2011, 74, 116501.
13. T. Huang, Z. Liu, G. Huang, R. Liu and Y. Mei, Nanoscale, 2014, 6, 9428.
14. P. X. Gao, Y. Ding, W. Mai, W. L. Huahes, C. Lao and Z. L. Wang, Science, 2005, 309, 1700.
15. R. Cui, Z. Han and J. J. Zhu, Chem.–Eur. J., 2011, 17, 9377.
16. H. Yoo, J. I. Lee, H. Kim, J. P. Lee, J. Cho and S. J. Park, Nano Lett., 2011, 11, 4324.
17. E. Akatyeva and T. Dumitrică, Phys. Rev. Lett., 2012, 109, 035501.
18. D. J. Bell, L. X. Dong and B. J. Nelson, Nano Lett., 2006, 6, 725.
19. C. Cao, H. Du, Y. Xu, H. Zhu, T. Zhang and R. Yang, Adv. Mater., 2008, 20, 1738.
20. X. Chen, S. Zhang, D. A. Dikin, W. Q. Ding and R. S. Ruoff, Nano Lett., 2003, 3, 1299.
21. H. F. Zhang, C. M. Wang, E. C. Buck and L. S. Wang, Nano Lett., 2003, 3, 577.
22. P. X. Gao, W. Mai and Z. L. Wang, Nano Lett., 2006, 6, 2536.
23. Y. Fu, J. L. Li and C. B. Cao, Phys. Chem. Chem. Phys., 2014, 16, 14808.
24. Z. Usman, C. B. Cao, G. Nabi, D. Y. Kun, W. S. Khan, T. Mehmood and S. Hussain, J. Phys. Chem. A, 2011, 115, 6622.
25. Z. Usman, C. B. Cao, W. S. Khan, T. Mahmood, S. Hussain and G. Nabi, J. Phys. Chem. A, 2011, 115, 14520.
26. Y. Q. Chen, X. N. Zhang, Q. Zhao, L. He, C. K. Huang and Z. P. Xie, Chem. Commun., 2011, 47, 6398.
27. K. M. Lee, T. Y. Choi, S. K. Lee and D. Poulikakos, Nanotechnology, 2010, 21, 125301.
28. H. B. Lu, B. C. Y. Chan, X. L. Wang, H. T. Chua, C. L. Raston, A. A. Yaron, M. Levy, R. P. Riro, R. T. Tenne, D. Feuermann and F. M. Gordon, Nanotechnology, 2013, 24, 335603.
29. X. N. Zhang, Y. Q. Chen, Z. P. Xie and W. Y. Yang, J. Phys. Chem. C, 2010, 114, 8251.
30. H. Cui, Y. Sun, G. Z. Yang, J. Chen, D. Jiang and C. X. Wang, Chem. Commun., 2009, 6243.
31. Y. Yang, H. Yang, G. D. Wei, L. Wang, M. H. Shang, Z. B. Yang, B. Tang and W. Y. Yang, J. Mater. Chem. C, 2014, 2, 4515.
32. H. F. Zhang, C. M. Wang and L. S. Wang, Nano Lett., 2002, 2, 941.
33. D. Zhang, A. Alkhateeb, H. Han, H. Mahmood and D. N. Mcllroy, Nano Lett., 2003, 3, 983.
34. P. B. Bandaru, C. Daraio, K. Yang and A. M. Rao, J. Appl. Phys., 2007, 101, 094307.
35. Z. J. Li, J. Zhao, M. Zhang, J. Y. Xia and A. L. Meng, Nano Res., 2014, 7, 462.
36. A. L. Meng, M. Zhang, W. D. Gao, S. B. Sun and Z. J. Li, Nanoscale Res. Lett., 2010, 6, 34.
37. Y. R. Lin, C. Y. Ho, C. Y. Hsieh, M. T. Chang, S. C. Lo, F. R. Chen and J. J. Kai, Appl. Phys. Lett., 2014, 104, 121909.
38. R. B. Wu, K. Zhou, Z. H. Yang, X. K. Qian, J. Wei, L. Liu, Y. Z. Huang, L. B. Kong and L. Y. Wang, CrystEngComm, 2013, 15, 570.
39. B. Krishnan, R. V. K. G. Thirumalai and Y. Koshka, Cryst. Growth Des., 2011, 11, 538.
40. X. H. Zhang, J. X. Gao, C. Q. Hong, J. C. Han and W. B. Han, CrystEngComm, 2013, 15, 7803.
41. H. Ma, L. Pan, Q. Zhao, Z. Zhao and J. Qiu, Carbon, 2012, 50, 778.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra07011a

---