Interactions between hydrogen and tungsten carbide: a first principles study

Abstract

Tungsten carbide has been proposed to be a potential inexpensive alternative to platinum for catalyzing hydrogenation reactions. Using density functional theory (DFT) calculations, we performed a systematic study on the geometries and electronic structures of small (WC)_n (n = 1–10) clusters. A cubic-like growth of WC clusters was found to be the preferred pathway. The interactions between the WC clusters and hydrogen were compared to interactions of hydrogen with the WC(0001) surface. Both atomic clusters and the crystalline surface of WC can lead to facile dissociation of H₂ while the activation energy on the former is even lower; the H diffusion barrier on WC clusters was found to be significantly higher than that on the WC(0001) surface, yet both of the calculated diffusion barriers are well above the values on the platinum counterpart. The lack of hydrogen mobility may exert a profound influence on the kinetics of hydrogen for participating in reactions on WC. The desorption strength of H on (WC)_n (n = 2, 4, 6, 9) at various hydrogen coverages was explored and the hydrogen saturated (WC)₉ cluster was used to rationalize the catalytic formation of hydrogen tungsten bronzes. The study provides insights which may be useful for efforts to replace Pt with WC in catalytic processes involving hydrogen.

---

1. Introduction

Early transition metal carbides have been widely used as cutting tools and hard-coating materials due to their strong hardness, high melting temperature and good electric and thermal conductivity.¹ From a chemical point of view, the landmark work on transition metal carbides by Levy and Boudart suggested that tungsten monocarbide exhibits similar catalytic properties to those found in platinum.² It was reported that WC manifests the similarity to Pt as a catalyst with respect to the reaction between H₂ and O₂ at room temperature, the formation of hydrogen tungsten bronzes (H_xWO₃) from WO₃ and the isomerization of 2,2-dimethylpropane.² It has since become an active subject of research to explore catalytic properties of WC for reactions such as hydrogenation of olefins^3,4 and hydrogen evolution reaction (HER) in which WC also serves as an electrode material.^5,6 In particular, HER has drawn considerable attention due to the potential application of hydrogen as a sustainable and carbon-free energy carrier.⁷ While Pt is currently used in electrode materials, the high cost and low global Pt reserves limit its practical use. Hence, tungsten carbide has been considered as a low cost alternative to Pt in HER applications.⁶ Despite the fact that significant advances have been made, the exchange current density characterizing the HER activity for WC is still 2–3 orders of magnitude below that of Pt, undermining its practical applications as a replacement. A monolayer Pt–WC structure (the so-called core–shell structure) was recently proposed^6,8 which would allow a significant reduction of Pt usage while maintaining comparable activity and efforts are underway to synthesize uniform metal shells and to achieve good control of the Pt–WC interface. To gain insight into the similar catalytic behavior between Pt and WC, the electronic transition resemblance of the anions of the two species was demonstrated via photoelectron spectroscopy, and it was concluded that WC is a superatom of a Pt atom.⁹ In addition, the behavior of hydrogen inside WC was investigated with first principles methods, aiming at shedding light to fusion reactor design.¹⁰ For catalytic hydrogenation, formation of hydrogen tungsten bronzes, and HER with WC as an electrode, however, H interacts with WC on the surface. An understanding of the surface interactions between WC and hydrogen is of fundamental importance, for which systematic investigations are needed.

Atomic clusters are amenable to theoretical treatment and have been used as a model for studying how material properties scale with an increasing size.¹¹ Bare and supported Pt-group metal clusters have been systematically investigated to understand chemical reactivity with hydrogen.^12–14 However, as a perceived “Pt-like” catalyst, the chemical properties of tungsten carbide clusters have rarely been addressed. To our knowledge, only (WC)_n (n = 1, 2, 4, 6, 12, 15, 36) clusters have been constructed to understand the mechanical strength of tungsten carbide.¹⁵ In the present study, we conducted a systematic study using DFT on hydride formation (the hydride nature of (WC)_nH_x is verified by charge analysis, vide infra) of small (WC)_n (n = 1–10) clusters with the objective to gain insight into the similarities and differences compared to Pt in catalyzing hydrogenation. The dissociative chemisorption of H₂ on selected WC clusters and the diffusion of H atoms upon adsorption were examined and compared with the reaction on a WC surface described by a periodic slab model. In particular, key catalytic properties of (WC)_n (n = 2, 4, 6, 9) including H₂ dissociative chemisorption energies and the maximum capacity for accommodating H atoms at full hydrogen saturation are addressed with the purpose of providing chemical insight into realistic catalytic processes in which catalyst surfaces are fully covered by hydrogen at a finite pressure.¹⁶ This work is organized as follows: the computational methodology is briefly discussed in section 2; the geometries of (WC)_n are presented in section 3.1, the dissociative adsorption and diffusion of hydrogen on a bare (WC)₆ cluster is considered in section 3.2, the adsorption strengths of H on selected WC clusters with increasing hydrogen loading are presented in section 3.3. The adsorption, dissociation, and diffusion of hydrogen on the WC(0001) surface are discussed in section 3.4. The thermodynamics of H₂ chemisorption on WC(0001) was investigated in 3.5. Finally, we summarized this work in section 4.

2. Computational models and methods

Calculations of (WC)_n clusters and their hydrides were performed using density functional theory (DFT) with the PBE¹⁷ functional as implemented in DMol³ package.^18,19 A randomized algorithm^20,21 was employed to search for stable configurations of (WC)_n (n = 2–6) using a minimum numerical (MIN) basis set (see ref. 20 and 21 for details). These minimum energy structures are then reoptimized using a double numerical basis set augmented with polarization functions (DNP) with core electrons described by an effective core potential (ECP). The transition states (TS) H₂ dissociation and H diffusion were bracketed using the LST/QST method.²² To avoid prohibitive computational difficulty, larger (WC)_n (n = 7–10) clusters were generated by sequentially grafting W–C pairs to the lowest energy structure of (WC)₆ at probable positions, followed by geometry optimization. The Hirshfeld population analysis²³ was performed to analyze the charge distribution. The binding energy of the (WC)_n cluster is defined as is defined as E_bind = [nE_W + nE_C − E_(WC)n]/n, (n = 1–10) where E_W, E_C and E_(WC)n represent energies of W atom, C atom and (WC)_n clusters respectively.

The chemical reactivity of hydrogen on the WC(0001) surface was computed using the periodic DFT method as implemented in the Vienna ab initio simulation package (VASP).^24,25 Bulk WC adopts either a hexagonal α-WC lattice or a cubic β-WC lattice.¹⁵ The former is more stable below 2525 °C with the W-terminated (0001) surface being most stable, which is therefore selected in the present study.¹⁵ A (3 × 3) cell of the WC(0001) surface was modeled as periodically repeating slabs consisting of three WC bilayers. A 15 Å vacuum layer was inserted between adjacent slabs (Fig. 1a and b). The projector-augmented wave method and the PBE functional were used with an energy cutoff of 400 eV. The Brillouin zone integration was sampled within a 3 × 3 × 1 Monkhorst–Pack k-point mesh.²⁶ Full structural optimizations with a conjugate-gradient method were performed until the forces became smaller than 0.05 eV Å⁻¹. We used the climbing-image nudged elastic band (CI-NEB)²⁷ method to calculate the minimum energy profiles along the prescribed reaction pathways.

Fig. 1 Structure of WC(0001) surface and H adsorption sites: (a) side view. (b) Top view. (c) Three possible H adsorption sites, the two atop sites of the W and C atoms (site W_T and C_T) and the center of hexagon formed by 3 C and 3 W atoms alternatively in a chair-like configuration (site C_3h). Gray sphere C, blue sphere W.

To verify the stability of (WC)_n clusters with full hydrogen saturation, we performed ab initio molecular dynamics (MD) simulations at 298 K for 6 ps with a time step of 1 fs in a NVE canonical ensemble. The MD simulations were conducted with VASP using a 20 × 20 × 20 ų box and Γ point for Brillouin zone sampling. The results of selected MD simulations are included in the ESI.†

3. Results and discussions

3.1 Bare (WC)_n clusters

The lowest energy structures of (WC)_n (n = 1, 2) and three minimum energy structures of (WC)_n (n = 3–10) are displayed in Fig. 2, where the relative stabilities and the symmetries are also labeled. No imaginary vibrational frequencies were found, suggesting that the obtained structures are at true energy minima. Furthermore, all electrons in the systems are fully paired, indicating a strong covalent interaction between W and C atoms.

Fig. 2 The optimized structures of (WC)_n (n = 1–10). For WC and (WC)₂, the most stable structures are shown; for (WC)_n (n = 3–10), the three lowest energy structures are illustrated, denoted as n–i for (WC)_n with i = 1–3. Symmetry and relative energy (in eV) with respect to the most stable isomer are also provided. Gray sphere C, blue sphere W. Cartesian coordinates of the most stable configurations are provided in ESI.†

The lowest energy structure of (WC)₂ was found to be planar while the trimer (3-1) is a 3D structure. The tetramer (4-1) adopts a distorted cubic structure, which can be viewed as a building block of larger WC clusters. Indeed, the lowest energy structures of larger clusters, i.e. 6-1, 8-1 and 9-1, as well as the less stable isomers including 8-2, 10-2 and 10-3 all exhibit an irregular cubic pattern, which is distinctively different from the hexagonal pattern in bulk tungsten carbide. The cubic feature can also be discerned in less regular clusters including 5-1, 7-1 and 10-1. Our results suggest that small (WC)_n clusters adopt a cubic structural growth pathway, which is consistent with the previous study.¹⁵

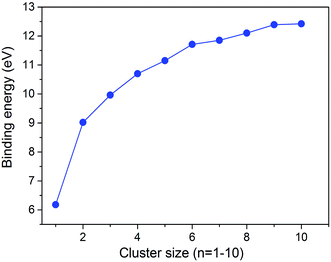
The calculated cluster binding energies of the minimum energy structures are presented in Fig. 3. As expected, the binding energy increases monotonically with the cluster size. We note that the calculated binding energy of (WC)₁₀ is still well below the calculated bulk cohesive energy of WC (16.05 eV),²⁸ and thus the properties of these small WC clusters may be distinctive from bulk WC.

Fig. 3 The calculated binding energies (eV) of the most stable (WC)_n (n = 1–10).

3.2 Dissociation and diffusion of hydrogen on WC clusters

In Pt catalyzed hydrogenation reactions, H₂ first undergoes dissociative chemisorption on surfaces of Pt catalyst particles²⁹ and, upon formation of metal hydrides, H atoms become highly mobile, an important characteristic of Pt-based catalysts. Therefore, for WC catalysts to behave truly like platinum, key catalytic properties such as H₂ dissociative chemisorption, the uptake capacity, and high H mobility with a low diffusion barrier on (WC)_n clusters must be similar to those on Pt clusters. In particular, the high mobility of H is expected to play an important role in the kinetics of hydrogenation and HER, as observed in the electrochemical experiment with Pt as an electrode.³⁰ To compare the interactions of hydrogen with platinum and tungsten carbide clusters, we chose a (WC)₆ cluster as an example for detailed analysis on H₂ dissociative chemisorption and H diffusion.

We first investigate H₂ dissociative adsorption and H diffusion at zero coverage. It has been shown that H₂ can be adsorbed on a solid surface via quasi-molecular bonding by lengthening the H–H bond to 0.9 Å.³¹ By sampling several initial configurations for H₂ to approach the (WC)₆ cluster, we identified the adsorption mode with H₂ on a vertex site W_ver being energetically most stable (Fig. 4). The H–H bond is elongated to 0.923 Å (R₁). The dissociation process is essentially barrierless (0.02 eV), similar to the case of H₂ dissociation on Pt clusters for which a very low barrier (0.05 eV) was reported.¹⁶

Fig. 4 The calculated energy diagram of H₂ dissociative chemisorption on (WC)₆ and the subsequent migrations of the H atoms on the cluster. The energies are relative to the sum of the energy of bare (WC)₆ and H₂. The hydrogen adsorption sites are also labeled, with C_edge, W_edge denoting edge sites and C_ver, W_ver denoting vertex sites respectively; H–H distances are labeled in parentheses, H–W (H–C) bond lengths are labeled in italic (in Å). Numbers of the imaginary frequencies for each transition state are given in italic. Gray C, blue W, green H (the same legend is used in Fig. 6, 7 and 9). Cartesian coordinates of all states are provided in ESI.†

The quasi-dissociative state of the H₂ molecule on the (WC)₆ cluster is attributable to the favorable interaction between the lowest unoccupied molecular orbital (LUMO) of H₂ and the highest occupied molecular orbital (HOMO) of the (WC)₆ cluster, as illustrated in Fig. 5. The total energy is lowered to −1.11 eV, accompanied by lengthening of the H–H distance to 1.990 Å (P₁). The H atoms can diffuse further to form the energetically most stable structure (P₅). The overall process is highly exothermic and the total energy is lowered by 2.46 eV (R₀ → P₅). To examine the mobility of H on (WC)₆, two H diffusion routes(P₁ → P₂ → P₅ and P₁ → P₃ → P₄ → P₅) were sampled. As displayed in Fig. 4, the former route where an H atom diffuses from W_ver to W_edge and further to another W_ver has an activation barrier of 0.73 eV. The activation barrier for the later route is much higher and thus less favored. The barrier of 0.73 eV is still significantly higher than the H diffusion barrier on Pt (0.23 eV), Pd (0.11 eV) and Ni (0.19 eV) clusters.¹³ The results suggest that H diffusion on the selected WC cluster at zero coverage is moderately difficult, in contrast to the facile diffusion of H atoms on Pt clusters. The significantly lower H mobility is expected to substantially diminish the catalytic activity of the material.

Fig. 5 The HOMO of the (WC)₆ cluster and the LUMO of H₂.

3.3 Hydrides of (WC)_n (n = 2, 4, 6, 9) clusters

One of the fundamental properties of a hydrogenation catalyst is the capability to accommodate H atoms. To gain detailed understanding, we systematically explored the sequential H₂ dissociative chemisorption processes on selected (WC)_n (n = 2, 4, 6, 9) clusters. These four clusters allow a variety of interacting configurations with hydrogen to be considered, e.g. (WC)₂ adopts a planar structure while the minimum energy structures of (WC)₄, (WC)₆ and (WC)₉ possess vertex, edge and face sites. For each WC cluster, H can be attached on either W or C atom. The sequential H adsorption is exemplified in (WC)₆ (Fig. 6) and the main observations from the calculated structures are summarized as follows:

Fig. 6 H₂ sequential dissociative chemisorption on a (WC)₆ cluster.

(1). Each W site is capable of accommodating 1–3 H atoms, depending on the coordination environment. The W atom of the planar (WC)₂ cluster can hold 3 H atoms while larger WC clusters with 3D structures can coordinate with two H atoms on a vertex site and one H atom on an edge site or a face site (the vertex site and edge site are depicted in Fig. 4 in (WC)₆ and the face site is shown in Fig. 7a in the (WC)₉ hydride).

Fig. 7 (a) The fully saturated hydrides of the selected (WC)_n (n = 2, 4, 6, 9) clusters, the face adsorption sites of (WC)₉ are also presented. Cartesian coordinates of the four configurations are available in ESI.† (b) The calculated H–W bond length distributions of the (WC)_n hydrides. g(r) was obtained by tabulating all the H–W distances at each step of the MD trajectories fitted with Gaussian functions.

(2). Each C atom can accommodate only one H atom.

(3). H atoms generally prefer W atoms first; the third H atom on W for the case of (WC)₂ is less preferred than on C; the preference of H on different W sites follows W_ver > W_edge > W_face, the second H on W_ver site has slightly lower adsorption strength than on C sites (detailed H adsorption strengths on various W and C sites of (WC)₆ and (WC)₉ are compared in Fig. S1†).

Structures with H atoms disobeying the rules usually display lower H₂ adsorption strength, as exemplified with (WC)₆ in Fig. S2.† The (WC)₂, (WC)₄, (WC)₆ and (WC)₉ clusters with full H-loading are displayed in Fig. 7a. The clusters can chemisorb up to 4, 6, 8 and 11 H₂ molecules, respectively. Room temperature MD simulations were performed to ensure that no H–H recombination occurs, as illustrated in Fig. S3.† To confirm that a cluster is at full H loading, additional H atoms to those “fully saturated” WC hydrides would result in formation of a H₂ molecule. The average H₂ adsorption energies and sequential H desorption energies of different H coverage are defined as:

E_ads = (2E_(WC)n + mE_H2 − 2E_(WC)nHm)/m, (1)

and

E_des = E_H − (E_(WC)nHm − E_(WC)nHm−2)/2, (n = 2, 4, 6, 9 and m = 2, 4, 6…), (2)

respectively, where E_(WC)n, E_H, E_H2 and E_(WC)nHm(E_(WC)nHm−2) denote energies of (WC)_n cluster, H atom, H₂ and (WC)_n hydrides. The calculated E_ads and E_des together with the calculated Hirshfeld charge gain per H atom are displayed in Fig. 8.

Fig. 8 (a) The calculated average H₂ adsorption energies; (b) the H desorption energies and (c) the average Hirshfeld charge gain per H atom for (WC)_n (n = 2, 4, 6, 9) clusters vs. H coverage.

We observe certain irregular behavior ((WC)₉H₄) in the E_ads plot, which is largely due to the structure relaxation induced by hydrogen adsorption. However, the overall trend of E_ads in the four cases decreases as H loading increases, as expected. In view of the fact that W atoms can accommodate more H than C at full H-loading and is energetically more favorable, the W–H bond is considered to be the main contribution to the adsorption strength. Therefore, the W–H bond length distribution g(r) is used to characterize H adsorption (Fig. 7b). The position of the peak of g(r) increases with cluster size. The bond length rationale is consistent with the calculated H₂ dissociative chemisorption energies (Fig. 8a) which shows that hydrogen adsorption strength on (WC)_n at full H-loading decreases with increasing cluster size within a narrow energy range (1.0–1.3 eV), similar to the narrow range of hydrogen adsorption strength for Pt_n (0.9–1.1 eV), Pd_n (0.6–0.8 eV) and Ni_n (0.8–1.1 eV).¹³ In parallel, the desorption energy of an H atom from fully saturated (WC)_n (n = 2, 4, 6, 9) (Fig. 8b) also varies within a narrow range (2.15–2.49 eV). Again, the energy is in a similar range from 2.08 eV to 2.73 eV as reported previously for hydrogen adsorption on small Pt, Pd and Ni clusters.¹³ With an increase of H-loading, the bonding nature of the metal hydrides evolves from metallic to covalent, leading to localized chemical properties and the narrowness of chemisorption and the desorption energies at full H-loading.¹³ The capacity of accommodating hydrogen atoms for WC is smaller than Pt of the same size. For example, Pt₉ can accommodate 34 H atoms, as compared with 22 H for (WC)₉. In comparison, Pd clusters have comparable hydrogen uptake to that of WC clusters (22 H for Pd₉), while the H capacity of Ni was found to be slightly lower than the value of both Pd and WC clusters (18 H for Ni₉). We note here that the topological geometries of (WC)_n clusters and their hydrides differ significantly from their counter-parts of nickel family clusters and the corresponding hydrides since the “super-atom” structure is not spherical.

As established in the previous section, the dissociative chemisorption of hydrogen on WC is facile. Another prerequisite for the WC catalyzed formation of H_xWO₃ is the facile H migration from WC to a substrate. Here, we consider the WO₃(001) surface as the substrate. Thermodynamically, for this process to occur, the H adsorption strength on the WO₃ surface must be stronger than the H desorption strength on WC. Indeed, the calculated E_des values for (WC)₆ and (WC)₉ at full H-loading are smaller than the reported H adsorption strength on the WO₃(001) surface (2.84 eV),³² making the H migration process thermodynamically feasible. The slow kinetics of the WC catalyzed spillover might be attributable to the low hydrogen mobility (see Fig. 4). Obviously, if a (WC)_n cluster is not fully saturated by H atoms, H-migration to the substrate surface may not occur. For example, the H desorption energy of (WC)₉H₁₄ was calculated to be 2.97 eV, which is larger than the H adsorption strength on the WO₃(001) surface. For most practical hydrogenation processes, the hydrogen pressure would be large enough so that the WC cluster would be fully saturated. The “full-saturation” scenario may also be applicable to model other reactions where WC serves as a catalyst. The hydride nature of (WC)_nH_x is reflected by charge analysis (Fig. 8c), which shows that H is negatively charged at various hydrogen coverage. This is similar to small Pt, Pd and Ni clusters, which also form hydride upon hydrogen adsorption, indicating that the hydrogen adsorbed on WC would be nucleophilic. The average partial charge gain per H atom essentially decreases with increased H loading in all cases, consistent with the corresponding trends of E_ads. Again, the discrepancy of a few points is attributed to the structure relaxation induced by hydrogen adsorption.

3.4 Dissociation and diffusion of hydrogen on WC(0001) surface

To compare the results obtained from the cluster model, the dissociation and diffusion of hydrogen on the W-terminated WC(0001) surface were investigated with a periodic model. Here, we consider only the low coverage case. Three types of hydrogen adsorption sites on the WC(0001) surface were identified, as illustrated in Fig. 1b and c. Atomic H adsorption strength was examined on W_T, C_T and C_3h respectively and calculated as E_ads = E_WC(0001) + 1/2E_H2 − E_H/WC(0001). C_3h (1.00 eV) and C_T (0.80 eV) were identified to be the stable sites. The calculated adsorption energy on the energetically more stable site C_3h agrees quite well with the reported H adsorption of 0.99 eV on the WC(0001) surface.⁶ W_T was found to be the most favorable H₂ adsorption site (Fig. 9), upon which the H–H bond is lengthened to 0.853 Å (R₁). Complete H₂ dissociation needs to surmount a barrier of 0.25 eV and the two H atoms are relocated to the nearby C_3h sites (P₁) with an H–H distance of 2.931 Å. For comparison, the reported energy barriers of H₂ dissociation on a typical Pt(111) surface are scattered in a wide range (0.06–0.42 eV).²⁹ The calculated H₂ dissociation energy on WC(0001) falls into this energy range. The results suggest that H₂ scission occurs more readily on (WC)₆ than on a crystalline surface, probably because H₂ displays more spatial freedom to adjust its position on a small cluster and thus facilitates electron transfer from the HOMO of the cluster into the LUMO of H₂. To examine the diffusion of H on the WC surface, H was allowed to migrate between two neighboring C_3h sites with the less favorable C_T site visited in the midway (P₁ → P₂ → P₃). The calculated diffusion barrier was found to be 0.40 eV, which is noticeably lower than that on the (WC)₆ cluster. However, this barrier is still significantly larger than that on a Pt surface, which was measured to be 0.07 eV by an experimental method or 0.05 eV derived from a DFT calculation.³⁰ The H diffusion barriers on both the WC(0001) surface and the atomic cluster are significantly higher than on the platinum counterpart, indicating a much lower hydrogen mobility on WC. This is consistent with the experimental observation that WC is much less catalytically active than Pt in hydrogenation reactions and in HER.^4,6

Fig. 9 Energetic profile of H₂ dissociation and H diffusion on WC(0001) surface; the energies are relative to the sum of the energy of WC(0001) slab and H₂. The concerned H–H (in parentheses) and W–H distances are labeled in Å. In R₁, P₁ and P₃, the two H have the same coordination environment, hence only one W–H distance is presented for each state.

A previous study proposed a volcano relationship to correlate the log of exchange current density with hydrogen binding energy on surfaces of an electrode to explain the HER activity of various cathode materials.⁶ The d-band center theory has also been a widely-used indicator describing activity or selectivity of a catalyst.³³ However, a correlation between kinetics of a catalytic hydrogenation reaction and H diffusion barrier has not been well understood. Empirically, the low H mobility is chiefly responsible for the mediocre performance of the WC catalyst, which suggests that H diffusion barriers should be an important parameter to be considered for design of new catalysts.

3.5 The thermodynamics of H₂ chemisorption on WC(0001)

Finally, we examine the thermodynamics of H₂ chemisorption on a WC crystalline surface. We estimated the equilibrium adsorption pressures of hydrogen chemisorbed on WC(0001), with the adsorption configuration P₃ in Fig. 9 being adopted. The Gibbs free energy of the adsorption process can be calculated as:³⁴

ΔG = G(2H/WC(0001)) − G(WC(0001)) − G(H₂) (3)

expressed in terms of enthalpies and entropies of the individual components, eqn (3) becomes:

ΔG = ΔH − T[S(2H/WC(0001)) − S(WC(0001)) − S(H₂)] (4)

We then approximate the reaction enthalpy with the calculated reaction energies ΔE since the reaction enthalpy does not change with temperature significantly. The entropic change from WC(0001) and 2H/WC(0001) is much smaller than the gas phase entropy of molecular H₂ and thus is neglected. Then eqn (3) becomes

ΔG ≈ ΔE + TS(H₂) (5)

or expressed with equilibrium constantwhere S(H₂) at various temperature is retrieved from the NIST database.

The equilibrium pressure of hydrogen at a given temperature is plotted in Fig. 10. Remarkably, the equilibrium temperature for H₂ at a partial pressure of 1 atm is ca. 1010 K, which suggests that WC can retain its catalytic activity up to high temperature.

Fig. 10 Equilibrium pressure of hydrogen chemisorbed on WC(0001) at a given temperature.

4. Summary

Unraveling the interaction of WC with hydrogen is key to understanding the catalytic properties of WC for reactions involving hydrogen. In the present study, we first explored the geometries of (WC)_n (n = 1–10) clusters and a cubic-like growth pattern was identified. H₂ dissociation and H diffusion on (WC)₆ cluster and WC(0001) surface were then investigated. It was found that H₂ dissociation on (WC)₆ has a lower barrier than that on WC(0001) surface. In contrast, the H diffusion barrier is noticeably higher on the atomic cluster. While the dissociation barrier of H₂ on tungsten carbide is comparable to that on platinum, hydrogen diffusion on WC is much less facile than on Pt, as revealed by results for both cluster model and slab model.

Hydrogen adsorption strength of (WC)_2,4,6,9 at various hydrogen coverage were obtained. Both the H₂ adsorption energies (E_ads) and H desorption energies (E_des) of fully saturated (WC)_nH_x clusters lie within a narrow range. The E_des of (WC)_2,4,6,9 are comparable to the corresponding Pt_n of the same size. We use the E_des of (WC)₉ at full H-loading to account for the H migration from tungsten carbide to tungsten oxide, for which the full saturation model is highlighted. Thermodynamics analysis reveals that tungsten carbide can retain its catalytic activity at relatively high temperature.

The elucidated inert diffusion behavior of H on tungsten carbide appears to be the primary reason for the relatively low catalytic activity of tungsten carbide. We expect this study can provide useful insight into the catalytic behavior of tungsten carbide and shed a light for design of efficient, low cost hydrogenation catalysts.

Conflict of interest

The authors declare no competing financial interest.

Acknowledgements

The authors gratefully acknowledge support of a Start-up grant from NUS, a POC grant from National Research Foundation of Singapore, a Tier 1 grant from Singapore Ministry of Education, a DSTA grant, a National Natural Science Foundation of China grant (no. 21233006) and NSF Grant No. PHY-1203228.

References

1. H. H. Hwu and J. G. Chen, Chem. Rev., 2004, 105, 185–212.
2. R. B. Levy and M. Boudart, Science, 1973, 181, 547–549.
3. C. Moreno-Castilla, M. A. Alvarez-Merino, F. Carrasco-Marin and J. L. G. Fierro, Langmuir, 2001, 17, 1752–1756.
4. X. Cui, X. Zhou, H. Chen, Z. Hua, H. Wu, Q. He, L. Zhang and J. Shi, Int. J. Hydrogen Energy, 2011, 36, 10513–10521.
5. D. V. Esposito, S. T. Hunt, A. L. Stottlemyer, K. D. Dobson, B. E. McCandless, R. W. Birkmire and J. G. Chen, Angew. Chem., Int. Ed., 2010, 49, 9859–9862.
6. D. V. Esposito, S. T. Hunt, Y. C. Kimmel and J. G. Chen, J. Am. Chem. Soc., 2012, 134, 3025–3033.
7. D. Kong, J. J. Cha, H. Wang, H. R. Lee and Y. Cui, Energy Environ. Sci., 2013, 6, 3553.
8. D. V. Esposito and J. G. Chen, Energy Environ. Sci., 2011, 4, 3900–3912.
9. S. J. Peppernick, K. D. D. Gunaratne and A. W. Castleman, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 975–980.
10. X.-S. Kong, Y.-W. You, C. S. Liu, Q. F. Fang, J.-L. Chen and G. N. Luo, J. Nucl. Mater., 2011, 418, 233–238.
11. S. V. Didziulis, K. D. Butcher and S. S. Perry, Inorg. Chem., 2003, 42, 7766–7781.
12. S. J. Tauster, Acc. Chem. Res., 1987, 20, 389–394.
13. C. Zhou, S. Yao, Q. Zhang, J. Wu, M. Yang, R. C. Forrey and H. Cheng, J. Mol. Model., 2011, 17, 2305–2311.
14. Y. Liu, W. Cen, G. Feng, Y. Chu, D. Kong and H. Yin, Appl. Surf. Sci., 2014, 313, 424–431.
15. V. G. Zavodinsky, Int. J. Refract. Met. Hard Mater., 2010, 28, 446–450.
16. C. Zhou, J. Wu, A. Nie, R. C. Forrey, A. Tachibana and H. Cheng, J. Phys. Chem. C, 2007, 111, 12773–12778.
17. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
18. B. Delley, J. Phys. Chem., 1996, 100, 6107–6110.
19. B. Delley, J. Chem. Phys., 2000, 113, 7756–7764.
20. M. Saunders, J. Comput. Chem., 2004, 25, 621–626.
21. J. Tong, Y. Li, D. Wu, Z.-R. Li and X.-R. Huang, J. Phys. Chem. A, 2011, 115, 2041–2046.
22. T. A. Halgren and W. N. Lipscomb, Chem. Phys. Lett., 1977, 49, 225–232.
23. F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138.
24. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
25. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
26. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
27. G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904.
28. F. Marinelli, A. Jelea and A. Allouche, Surf. Sci., 2007, 601, 578–587.
29. J. K. Vincent, R. A. Olsen, G. J. Kroes and E. J. Baerends, Surf. Sci., 2004, 573, 433–445.
30. J. Fearon and G. W. Watson, J. Mater. Chem., 2006, 16, 1989.
31. P. Jena, J. Phys. Chem. Lett., 2011, 2, 206–211.
32. Y. Xi, Q. Zhang and H. Cheng, J. Phys. Chem. C, 2014, 118, 494–501.
33. M. P. Humbert, L. E. Murillo and J. G. Chen, ChemPhysChem, 2008, 9, 1262–1264.
34. M. Yang, B. Han and H. Cheng, J. Phys. Chem. C, 2012, 116, 24630–24638.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra06225f

---