Conformational and zwitterionic preferences of N-amidinoglycine: the effect of microsolvation and metal ion addition

Abstract

N-Amidinoglycine (NG) is a precursor of creatine, which is the energy source in muscles and plays a vital role in adenosine triphosphate homeostasis. NG possesses the combined structural properties of Gly and Arg. Extensive work on cationic complexation, anionic complexation, microsolvation, excess electron binding, etc. is reported on Gly as well as Arg. Quantum chemical calculations have been performed using B3LYP, BHandHLYP, ωB97XD, M06, M06-2X and MP2 methods, on NG to understand the conformational and zwitterionic preferences under the influence of metal ions (alkali and alkaline earth ions) and water coordination, as well as on the bare structures. NG can have many alternative structures; at least ten structures are possible within 5 kcal mol⁻¹, in the gas phase. NG-1 and NG-2 are highly competitive structures as global minima. The zwitterion (ZNG-1) is about 15 kcal mol⁻¹ less stable than the canonical form (NG-2) in the gas phase although its basicity is high as Arg. This unusual instability of the zwitterionic form of NG may be attributed to the lack of intramolecular self-solvation (multiple hydrogen bonding between the guanidine and carboxylate groups) which is found in Arg. Microsolvation decreases energy differences between canonical and zwitterionic forms of NG, three water molecules are necessary to make them energetically competitive. Computational analysis indicated that the relative stabilities of canonical conformers and zwitterions of NG are very sensitive to their surroundings. Salt bridge structures of NG with alkali and alkaline earth metal cations are stable over charge solvated structures by about 2–8 and 1–14 kcal mol⁻¹, respectively, except in the case of the Be⁺² ion.

---

Introduction

N-Amidinoglycine (NG) (also known as guanidinoacetic acid) (Fig. 1) is a biologically important molecule, synthesized in the kidney from glycine (Gly) and arginine (Arg) as a result of transamidation in the presence of glycineamidinotransferase enzyme.¹ NG is considered as a metabolic product of glycine, in which the amino group of glycine is replaced by a guanidino group.² NG is a precursor of creatine (CR), which is the most important energy source in muscles and plays a vital role in ATP homeostasis.³ NG along with CR have been used as important diagnostic markers for inborn errors in creatine biosynthesis, transport and renal diseases.⁴ In addition, NG, CR (and creatinine) have been suggested as diagnostic tools for the detection of transferase enzymes deficiencies.^5,6 Moreover, NG is involved in a number of biological processes such as insulin regulation, renal metabolism, thyroid dysfunction, neuromodulator, etc.^7–9 Its accumulation leads to neurotoxic and epileptogenic action.¹⁰

Fig. 1 Structures of glycine, arginine, N-amidinoglycine and creatine.

Most of the amino acids are known to exist in the canonical form as the lowest energy structure in the gas phase and in the zwitterionic form in solution, crystalline phase, biological condition, etc. The relative energy difference between canonical and zwitterionic forms of amino acids can be decreased in the presence of additional intermolecular interactions. For example, the simplest amino acid, Gly exists in a canonical form in the gas phase and its zwitterion is reported to be 16–20 kcal mol⁻¹ less stable than canonical form.^11–13 Jensen et al.¹¹ reported that two water molecules are required to stabilize the zwitterion of Gly in the gas phase. In the cluster of Gly with 1–6 water molecules, canonical form is favored over the zwitterionic form however, in the presence of seven water molecules canonical and zwitterionic structures are isoenergetic.¹⁴ The solvation of zwitterionic and canonical forms of Gly by excess electron indicated that its zwitterion is stabilized by about 8 kcal mol⁻¹ compared to canonical form.¹⁵ The counterions (cations and anions) also help in stabilizing the zwitterionic or canonical structures of amino acids in the form of salt bridge or charge solvated structures. For example, Gly forms charge solvated structure in the presence of Na⁺ and Rb⁺ ions, of which rubidiated structures are strongly preferred.¹⁶ For the smaller alkali metal ions, NO-coordinated structures (in which the ion is coordinated with nitrogen of the amino group and the carbonyl oxygen) are preferred while for larger ions, OO-coordinated structures are preferred.¹⁷ In the N-methylated or N,N-dimethyl Gly, sodiated and rubidiated salt bridge structures are more stable than the charge solvated structures by 1–7 kcal mol⁻¹.¹⁶ Strittmatter et al.¹⁸ studied the complexation of Gly with alkaline earth metal ions and reported that the salt bridge structures are 5–12 kcal mol⁻¹ more stable than the charge solvated structures for all metals except Be²⁺ ion where, the charge solvated structures were found more favorable by 5–8 kcal mol⁻¹.

On the other hand, Arg is the most basic amino acid compared to all other amino acids, and its zwitterion is reported to be only 1–3 kcal mol⁻¹ less stable than the canonical form.^19–21 The zwitterion of Arg is found to be more stable than the canonical form in the presence of one water molecule by about 2.0 kcal mol⁻¹.²² Skurski et al.²³ reported that in the presence of the excess electron, zwitterionic structure of Arg becomes quasidegenerate with a canonical form. Cerda et al.²⁴ reported that Arg with smaller alkali ions (Li⁺ and Na⁺) forms charge solvated structures, while with larger metal ions (K⁺ and Cs⁺) it prefers to form the salt bridge structures. Jockusch et al.²⁵ reported that the salt bridge structure of Arg becomes more stable as compared to the charge solvated structure with an increase in size of alkali metal ions. For example, Li⁺ ion forms 0.7 kcal mol⁻¹ more stable charge solvated structure while Na⁺ forms 0.7 kcal mol⁻¹ more stable salt bridge structure, and K⁺ to Cs⁺ form salt bridge structures with 3–4 kcal mol⁻¹ higher energy preferences. Bush et al.²⁶ showed that Ca²⁺, Sr²⁺ and Ba²⁺cationized structures are zwitterionic while Be²⁺ and Mg²⁺cationized structures are nonzwitterionic. The stability of alkaline metal cationized zwitterionic Arg increases as a function of alkaline earth ions size as reported for alkali metal cationized Arg. Remko et al.²⁷ found that Arg complexes with Li⁺/Na⁺/Cu²⁺ are non-zwitterionic, while in the presence of one water molecule, complexes are reported to be zwitterionic.

NG is not a natural amino acid, however; it contains all important characteristic of natural amino acids. NG carries both basic (guanidino) and acidic (carboxylic acid) groups similar to amino acids and hence, it can exist in either zwitterionic or neutral (nonzwitterionic) forms. NG can be considered to possess the structural properties of Gly and Arg. In comparison, NG, like Arg has a strong basic guanidine group in place of α-amino group and thus, it is expected to form the stable zwitterion compared to Gly. Similarly, like Gly, only one methylene group separates the acidic and basic groups and an additional amidine group is present at α-amino group. Initial study indicated that the proton affinity and gas phase basicity of NG (240 and 233 kcal mol⁻¹) are very close to that of Arg (247 and 240 kcal mol⁻¹) compared to Gly (211 and 203 kcal mol⁻¹).²⁸ It can be hypothesized that NG zwitterion may have similar stability (∼3 kcal mol⁻¹) as that of Arg. de Miranda et al.²⁹ reported the coordination behavior of NG with some ions of biological interest using potentiometric study and proposed that in the most probable structure of complexes, the metal ion interacts with α-nitrogen and carbonyl oxygen. Wyttenbach et al.³⁰ indicated the presence of one zwitterionic and three canonical structures for NG. Of which sodiated and rubidiated salt bridge structures were found to be ∼9–10 kcal mol⁻¹ more stable than charge solvated structures. Considering it as a model system for Arg, they hypothesized that Arg forms similar salt bridge structures. Ramos et al.³¹ synthesized a novel complex glycinate–guanidoacetate nickel(II) of Ni(II) with NG and Gly, and observed that both (NG and Gly) coordinated with Ni(II) through NO coordination. Similar complexes of NG are reported with other amino acids like glutamate, serine, etc.^32,33

Although the above reported studies indicated the presence of canonical and zwitterionic forms for NG, to the best of our knowledge, a detailed study of preferred isolated (canonical, tautomeric and zwitterionic) forms, hydrated, and metal cationized forms, has not been explored. Environment affects the tautomeric preferences, depending on the polarity; therefore, it is valuable to explore the effect of solvents because tautomeric/zwitterionic preferences play an important role in drug action, stability, reactivity, determining their pK_a/PD values, etc. In addition, NG has been used extensively as a ligand in metal complexes. How are different metals coordinated with NG? How metals affect the preference of canonical and zwitterionic forms? What would be the preferred coordination mode (OO or NO)? NG is considered as a structural analogue of Gly and Arg because it has a basic moiety of both of them. Numerous studies on cationic coordination, anionic complexation, excess electron binding, microsolvation, derivatization have been reported for Arg and Gly amino acids. However, no such attempt has been made to understand the (metal and water) coordination behavior, and canonical and zwitterionic preferences of NG. It would be very interesting to see how water and metal cations coordination behavior of NG would be comparable with that of Gly or Arg. The initial computational study indicated that the proton affinity and basicity of NG are comparable with Arg whereas its zwitterion stability is closer to that of Gly. To explore these phenomena, quantum chemical analysis has been carried out on microsolvated and metal cationized NG, and compared with that of Gly and Arg.

Computational methodology

Ab initio molecular orbital (MO)^34,35 and Density Functional Theory (DFT)^36,37 calculations were carried out using GAUSSIAN09³⁸ software package. Complete optimization of various conformers, tautomers, zwitterionic states were performed using B3LYP,^39,40 BHandHLYP^41,42 and MP2⁴³ methods with 6-31+G(d,p) and 6-311++G(d,p) basis sets. In addition, some calculations were carried out using Aug-CC-pVDZ basis set at B3LYP and MP2 levels. Finally, all these structures were optimized at M06-2X⁴⁴ level using 6-311+G(2df,p) and MG3S^45,46 basis sets. For all the optimized structures, frequencies were computed analytically to characterize stationary points as minima or transition states. Each transition state was characterized by first-order saddle point with only one imaginary vibrational mode on the potential energy surface. Solvent phase optimization was carried out using the polarizable continuum model CPCM⁴⁷ and SMD⁴⁸ methods on selected conformations and water-complexes to understand the influence of the solvent medium. In order to understand the effect of bulk water, microsolvation calculations were carried out on selected geometries in the presence of 1–6 water molecules using B3LYP/6-311++G(d,p), B3LYP/Aug-cc-pvdz, and ωB97XD⁴⁹/6-311++G(d,p) levels of theory. The alkali and alkaline earth metal cation complexes were optimized using B3LYP/6-31+G(d,p), B3LYP/6-311++G(d,p), BHandHLYP/6-311++G(d,p), M06⁴⁴/6-311++G(d,p) and M06-2X/6-311+G(2df,p) levels of theory. For heavy elements like Rb, Cs, Sr and Ba LANL2DZ basis set was used.

Results and discussion

In this study results are presented in three sections (i) conformational, tautomeric and zwitterionic preferences (ii) microsolvation of canonical and zwitterionic structures (iii) alkali and alkaline earth metal cationized complexes of NG.

Electronic structure analysis of NG conformations, tautomers and zwitterions

On the basis of reported conformations of Gly and chemical intuition, we proposed about 20 initial structures. From them 15 found to be stable on the potential energy surface and others are converged to stable structures during optimization. The relative energy data for six different isomers (NG-1 to NG-6) and two zwitterionic isomers (ZNG-1 and ZNG-2) is given in Table 1 and their optimized structures are given in Fig. 2 (others in ESI†). The two structures NG-1 and NG-2 are almost isoenergetic and compete for the global minimum state. Both of them are characterized by intramolecular H-bond and local anti-arrangement of carboxylic group. 1,3-H shift in the guanidine moiety of NG-1 and rotation across C4–N5 bond can lead to NG-2. NG-2 type conformation in Gly, is one of the lowest energy conformations. In NG-3, one of terminal nitrogen atoms of the guanidine group acts as H-bond donor to carboxylic group and it is 1.45 kcal mol⁻¹ less stable than NG-1 at BHandHLYP/6-311++G(d,p) level. NG-4 has extended conformation and it is only 2.18 kcal mol⁻¹ less stable on the relative scale. NG-5 is a 1,3-H shift tautomer of NG-3 conformation. Isomers NG-1, NG-3 and NG-5 adopt bent conformation; a structure in which (NG-1) carboxylic group acting as a H-bond donor is more preferred. 1,3-H shift in the guanidine moiety of NG-4 (from central nitrogen to terminal nitrogen) leads to NG-6 isomer (extended conformation), which is 4.0 kcal mol⁻¹ less stable than NG-1. Since the energy differences among six isomers are quite small, any of them can be accessible under equilibrium conditions.

Table 1 Relative energy (kcal mol⁻¹) of various conformations, tautomers and zwitterions of NG

Entry	Gas phase									Solvent
	HF	B3LYP	B3LYP	MP2	BHandHLYP	B3LYP	MP2	M06-2X		M06-2X
	6-31+G(d,p)		6-311++G(d,p)			Aug-CC-pVDZ		6-311+G(2df,p)	MG3S	6-311+G(2df,p)
NG-1	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
NG-2	−0.77	0.08	−0.14	0.33	−0.26	0.00	0.46	0.54	0.54	2.48
NG-3	0.00	1.79	1.85	1.19	1.45	2.01	1.48	1.56	1.64	6.57
NG-4	0.16	3.33	3.02	3.13	2.18	2.90	3.20	2.82	2.80	7.20
NG-5	1.60	4.41	4.27	3.76	3.49	4.33	3.97	4.08	4.10	8.22
NG-6	2.54	4.57	4.30	4.02	4.00	4.38	4.63	4.68	4.77	6.87
ZNG-1	16.28	—	—	—	14.46	—	—	—	—	−1.93
ZNG-2	11.90	—	—	—	—	—	—	—	—	−1.67

---

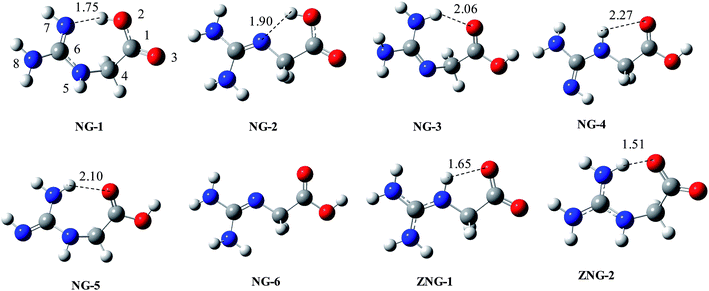Fig. 2 BHandHLYP/6-311+G(d,p) optimized geometries of various conformations, tautomers and zwitterions of NG (structure of ZNG-2 at HF/6-31+g(d,p)).

Proton shift from carboxylic group to basic guanidine group may lead to zwitterionic species ZNG-1 and ZNG-2. Unimolecular or bimolecular or cationic charge assisted proton transfer in NG-2, NG-4 and NG-6 can lead to ZNG-1 zwitterionic isomer, while the proton shift in NG-1, NG-3 and NG-5 can lead to ZNG-2.

The possibility of zwitterions is denied in the gas phase as per B3LYP/MP2 optimization (using 6-31+G(d,p), 6-311++G(d,p) and Aug-CC-pVDZ) because the zwitterionic structures are converted back to NG-1 or NG-2. These zwitterions also do not found at M06-2X/6-311+G(2df,p) and M06-2X/MG3S levels. The BHandHLYP/6-311++G(d,p) calculation indicated that zwitterionic isomer ZNG-1 can exist in gas phase while ZNG-2 revert to NG-1. The zwitterionic isomer, ZNG-1 is 14.72 kcal mol⁻¹ less stable than NG-2 at BHandHLYP/6-311++G(d,p) level. CPCM calculations indicated that both of zwitterions exist in solvent phase and are found to be about 1.7 to 1.90 kcal mol⁻¹ more stable than NG-1. On the relative scale NG-2 to NG-6 are estimated about 2–5 kcal mol⁻¹ higher energy in the solvent phase compared to the gas phase. NG is structurally very well resemble to Arg and its proton affinity as well as basicity are also comparable with that of Arg; therefore its zwitterion is expected to be near about 3 kcal mol⁻¹ less stable (as in Arg^19,21) than the corresponding canonical form. Comparatively, a zwitterionic preference of NG is about 12 kcal mol⁻¹ less than that of Arg in the gas phase. This low stability of NG zwitterion may be due to low self-solvating ability as compared to that of Arg. NG has only one carbon chain between carboxylic and guanidine groups compared to four carbon chain in Arg, therefore the guanidine group of Arg interacts with carboxylic and amino groups with multiple intramolecular H-bonds easily; such flexibility is absent in NG. The energy difference between canonical and zwitterionic forms of NG is more comparable to that of Gly (16–20 kcal mol⁻¹).

In order to understand this large (12 kcal mol⁻¹) relative energy difference in the canonical and zwitterionic forms of Arg and NG, the energy differences between canonical and zwitterionic forms of Arg homologous series (NH₂)₂–C=N–(CH₂)_n–(NH₂)COOH (n = 1–4) containing smaller carbon chain, are computed using BHandHLYP/6-311++G(d,p) level of theory. In this series, the ΔE between canonical and zwitterionic forms increases with a decrease in the carbon chain length (from 3 kcal mol⁻¹ to 12 kcal mol⁻¹) in the gas phase (Fig. 3). When n is large (3/4) the lowest energy isomers are characterized by multiple intramolecular H-bonds, because of greater flexibility. A decrease of ∼2.5 kcal mol⁻¹ energy is associated with each CH₂ group. The proton affinity of guanidine moiety remains almost same (242–247 kcal mol⁻¹) along the series. Similarly the energy differences between canonical and zwitterionic forms are computed in the congeneric series of NG, (NH₂)₂–C=N–(CH₂)_n–COOH (n = 1–4). In this series also the energy difference is quite dependent on the number of carbon atoms present in the linker unit, larger the n value smaller is the ΔE value. This clearly established that why NG zwitterionic preference (∼15 kcal mol⁻¹) resembles more to Gly (16–20 kcal mol⁻¹) rather than that of (∼3 kcal mol⁻¹) Arg though it has a highly basic guanidine group.

Fig. 3 Energy difference between the most stable canonical and zwitterionic forms of Arg and NG homologous series (n = 1–4).

Though there is minimal change in the proton affinity of the guanidine moiety, there is gradual change in the ΔE values. This observation confirms that the flexibility is a determining factor, rather than basicity. This observation is in contrast to the observation by Wyttenbach et al.¹⁶ who proposed that zwitterionic stability of amino acids have linear relationship with proton affinity.

Microsolvation

Structures of amino acids are very sensitive to the surrounding environment like the presence of cations or anions, solvent molecules, etc.^{14,18,23,25,50} Numerous studies on microsolvation have been reported on the molecules of biological importance (amino acids, neurotransmitters, drugs, etc.) in order to see their behavior in the presence of explicit water molecules.^14,51–57 These microsolvation studies on amino acids indicated that the probability of finding lowest energy configurations is somewhat high when water molecules bridge the two opposite nature functional groups (acidic and basic groups or positively and negatively charged groups) by water chain, water ring or water cage. In addition, multiple hydrogen bonds formation with ligand and among water molecules is also found to be desirable. In NG, both the guanidine and carboxylate (yl) groups are polar; therefore has very strong propensity for multiple hydrogen bonding. The number of water molecules evidently affects the canonical and zwitterionic preferences of amino acids. For example, to make zwitterionic and canonical forms energetically competitive with each other, minimum of three (for lysine),⁵⁸ five (for tryptophan),⁵⁹ and six (for cysteine and alanine)^52,60 water molecules are required. For the amino acids, Gly and Arg about seven¹⁴ and one²² water molecules respectively, are required to make canonical and zwitterionic structures comparable to each other. As mentioned in the introduction, NG has structural properties similar to that of Gly and Arg, and then it will be very interesting to see, how the microsolvation will affect the relative thermodynamic stabilities of the zwitterionic vs. canonical forms of NG, to explore this, the microsolvation behavior of NG in the presence of 1–6 water molecules is carried out.

Initially extensive search has been carried out to identify the most stable configurations of NG–(H₂O)_1–6 on the potential energy surface, using B3LYP/6-31+(d,p) method. Further these configurations were optimized at B3LYP/6-311++G(d,p), B3LYP/Aug-cc-pvdz and ωB97XD/6-311++G(d,p) levels of theory. Here, discussion is limited to ωB97XD/6-311++G(d,p) method because this functional captures the weak dispersion based interactions. The relative energies and structures of the lowest energy canonical and zwitterionic configurations of NG–(H₂O)_1–6 are given in Fig. 4. The relative energies and structural details of the other alternative water-clusters are reported in ESI (Table S1 to S3 and Fig. S3 to S5†). Addition of one water molecule to NG leads to the identification of fifteen canonical and four zwitterionic configurations of NG–H₂O cluster. In the lowest energy structure NG-1W, a water molecule is bridging the carbonyl oxygen (O3) of the carboxylic group and one of the NH group (N5–H) of guanidine moiety. The lowest energy zwitterionic structure ZNG-1W lies 3.64 kcal mol⁻¹ higher in energy than the most stable canonical form NG-1W. This monohydrated zwitterionic structure (ZNG-1W) is from ZNG-2, which does not exist in unsolvated condition. This stable zwitterion may be considered to have originated from canonical form NG-1W through hydrogen hopping. The water clusters ZNG-1W and NG-1W are structurally similar and differ only in the position of the hydrogen atom.

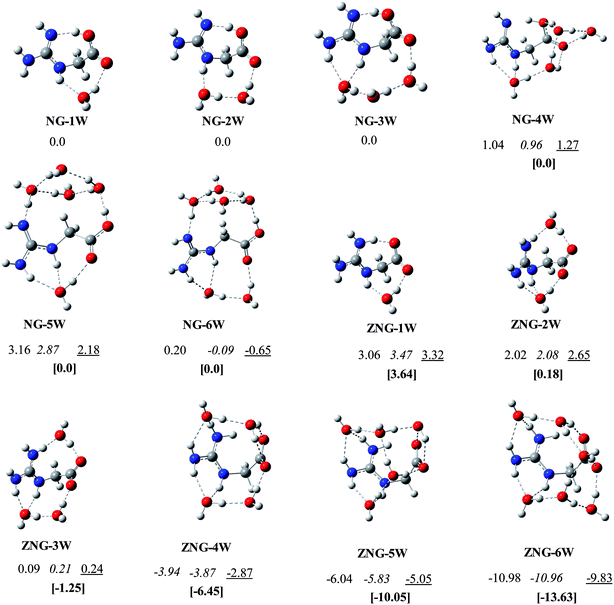Fig. 4 The lowest energy canonical and zwitterionic configurations of NG with 1–6 water molecules: B3LYP/6-31+G(d,p); B3LYP/6-311++G(d,p); B3LYP/aug-cc-pvdz; [ωB97XD/6-311++G(d,p)].

Eleven canonical and seven zwitterionic configurations of NG–(H₂O)₂ located on the potential energy surface. In the most stable canonical isomer NG-2W, a two water chain bridges across carbonyl (O3) and guanidine moiety (N5) (Fig. 4). In the lowest energy zwitterionic configuration ZNG-2W, two independent water molecules bridge guanidine and carboxylate groups at two different locations. A zwitterionic configuration (ZNG-2W-b) where a two water chain bridges across carbonyl and guanidine moiety is found to be ∼1 kcal mol⁻¹ less stable than NG-2W. The canonical configuration of microsolvated NG–(H₂O)₂ cluster is energetically comparable with the zwitterionic configuration at ωB97XD/6-311++G(d,p) level, however, at the other levels difference between them found to be ∼2 kcal mol⁻¹. (Fig. 4). These differences have arisen due to incorporation of weak interactions in long-range corrected hybrid functional ωB97XD.

Eighteen canonical and nine zwitterionic configurations of NG–(H₂O)₃ with three water molecules were identified. In the lowest energy configuration NG-3W, three water molecules orient themselves between carbonyl (O3) and two amino groups (N5, N7) of guanidine by a H-bonded three water chain. One of the water molecules of the chain form a bifurcated H-bond with guanidine group. The lowest zwitterionic configurations ZNG-3W can be obtained by adding one additional water molecule (near guanidine moiety) in the two water zwitterionic configuration ZNG-2W. The addition of one extra water to ZNG-2W, has improved the stability of ZNG-3W by about 1 kcal mol⁻¹. Zwitterion ZNG-3W is clearly more stable than the canonical form NG-3W by 1.27 kcal mol⁻¹. This indicates that for the NG–(H₂O)₃ three water molecules are sufficient to make NG zwitterion competitive with a canonical form. Here, it can be concluded that the transition of canonical configuration to zwitterionic configuration starts in the presence of three water molecules in contrast to Gly where at least seven water molecules are required.¹⁴ On the other hand, for Arg only one water molecule is required to make canonical and zwitterionic forms energetically comparable.²² This reveals that microsolvated zwitterion of NG resembles to microsolvated Arg zwitterion in term of number of water molecules (between 2–3).

Twenty five canonical and thirty zwitterionic configurations of NG–(H₂O)₄ with four water molecules were located. In the most preferred neutral configuration NG-4W, a twisted four-water chain is spanning between carboxylic group and guanidine group by making five hydrogen bonds with NG. Three water molecules of chain form three hydrogen bonds with carboxylic group while the other one water makes two hydrogen bonds with guanidine moiety. In the ZNG-4W, two independent chains of two water molecules orient themselves between carboxylate and guanidine group by making seven hydrogen bonds with NG. This zwitterionic structure is found to be 6.45 kcal mol⁻¹ more stable over canonical structure.

In the neutral pentahydrated and hexahydrated water configurations, a ring of four water molecules is found to be favorable across the hydroxyl and guanidine groups. Additional one/two water molecules orients between carbonyl oxygen and two NH of guanidine moiety. In their corresponding zwitterionic configurations, the presence of a chain of four/five water molecules (in U shape) is preferred across the NG molecule along with an additional interaction of a water molecule with carboxylate group.

In order to see the effect of bulk water solvent, these most stable canonical and zwitterionic configurations are subjected to SMD and CPCM solvent phase computation using a ωB97XD/6-311++G(d,p) level of theory. Results indicate that all the canonical configurations during optimization (with SMD model) converted back to corresponding zwitterionic configurations, by direct proton transfer to guanidine group from carboxylic group, in the presence of 1–3 water molecules. Moreover, water configurations (NG-2W and NG-3W) found to be unstable on the potential energy surface and revert to zwitterionic forms at CPCM model. The canonical NG-1W structure is found to be 7.23 kcal mol⁻¹ less stable than the zwitterionic ZNG-1W form.

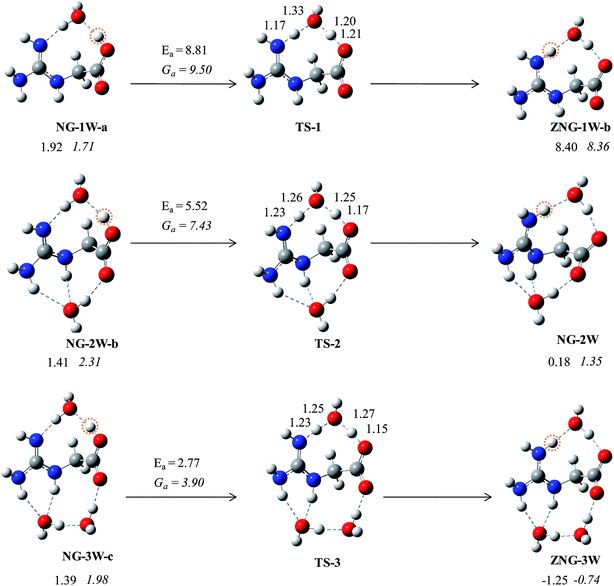
In the gas phase, the energy difference between canonical and zwitterionic forms is higher but in the microsolvated condition (n = 3), it is negligible. Therefore, the isomerization process of microsolvated canonical and zwitterionic forms may be a very feasible process. We have established a mechanism for proton transfer: from a canonical form to zwitterionic form (Fig. 5). In water-mediated mechanism, proton from carboxylic group transfers to guanidine group through a water molecule. In the transition states, two protons are transferred in a concerted way through a water molecule (Fig. 5). Such concerted mechanism has been established for lysine⁵⁸ and alanine⁵¹ amino acids rather than stepwise mechanism through hydronium ion. The estimated barriers for isomerization of NG-1W-a and NG-2W-b to ZNG-1W-b and NG-2W are about 8.81 and 5.52 kcal mol⁻¹, respectively. This indicates that proton transfer barrier is reduced by 3 kcal mol⁻¹ in the presence of an additional water molecule between guanidine and carbonyl groups. Moreover, barrier for proton transfer from NG-3W-c to ZNG-3W is found to be 2.7 kcal mol⁻¹. This shows that as the number of water molecules increases the proton transfer barrier get reduced. In the above cases one water molecule directly participates in the hydrogen transfer and the others play a supportive role in stabilizing the NG–(H₂O)_2–3 complexes.

Fig. 5 In NG–(H₂O)_n (n = 1–3) water mediated concerted double proton transfer mechanism for isomerization of canonical form to zwitterionic form (relative energy in kcal mol⁻¹ with respect to the most stable canonical configurations NG-1W/NG-2W/NG-3W, bond distances in Å, ωB97XD/6-311++G(d,p)). The values in normal and italic are the estimated electronic and Gibbs free energies. (The starting structures in each case are not the global minima).

Metal complexation of NG with alkali and alkaline earth cations

Complexation of several metal cations with amino acids have been investigated using experimental and quantum chemical studies in order to get insight how cations effect the stability of the salt bridge (SB) and the charge solvated (CS) structures.^{17,18,25–27,61–64} These studies can help in understanding of the metal interaction with enzymes, receptors, ion/ion-pairs channels, salt bridge structures of peptides, etc.^65–67

Many independent studies on the Gly-alkali metal cation complexes are reported, all of them point out that the salt bridge structures are not favorable because zwitterionic state is not sufficiently stabilized by the alkali metal ions.^17,68 Whereas for Gly-alkaline earth metal cation complexes, salt bridge structures are found to be stable except for Be²⁺ ion.¹⁸ Alternatively, the Arg–metal cation complexes mostly prefer to form salt bridge structures^24–26 (except Li⁺, Be²⁺ and Mg²⁺ cations), in which, the metal ion either coordinates to the oxygen atoms of carboxylate group or coordinates with both amino and carboxylate groups. In contrast, the NG–metal cation complexes (alkali and alkaline earth cations) prefer the salt bridge structures (except Be²⁺), the details are presented in this section.

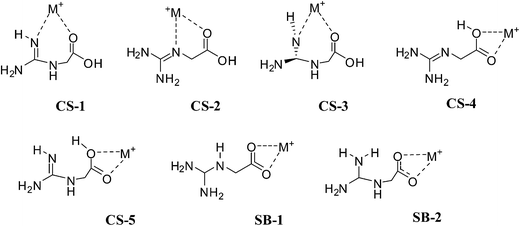
For the metal complexation, initial structures were proposed from the analysis of already reported metal complexes of Gly and Arg. Their analysis indicated that Gly can have mono- and bi-coordinated complexes while Arg bi- and tri-coordinated complexes. On the basis of this observation, we explored all possibilities for NG bound metal complexes. Finally, we observed only bi-coordinated complexes for NG bound alkali cations and bi and tri-coordinated complexes for alkaline earth cations. No mono-coordinated complex is found for NG as it is observed for Gly. (see ESI† for other initial guess).

Alkali metal cation complexation. The alkali metal cationized charge solvated and salt bridge structures of NG are shown in Fig. 6 and 7 (Na⁺ cation bound optimized structures), and their relative energies are given in Table 2. All the complexes are optimized using B3LYP/6-31+G(d,p), B3LYP/6-311++G(d,p), BHandHLYP/6-311++G(d,p), M06/6-311++G(d,p) and M06-2X/6-311+G(2df,p) levels of theory. M06-2X functional is used for the discussion because of its better performance, as it is recommended for applications involving the organometallic chemistry and noncovalent interactions.⁴⁴ The relative energy data on the other methods is reported in ESI Table S7.† Five charge solvated structures (CS-1 to CS-5) and two salt bridge structures (SB-1 and SB-2) may be possible. In the charge solvated structures CS-1 to CS-3, cations are chelated with the guanidine nitrogen (N5) and carbonyl oxygen (O3) through NO coordination, and in CS-4 and CS-5 cations are coordinated with both the oxygen atoms of carboxylic group (OO coordination), CS-5 is not found on the potential energy surface with any metal cations. The salt bridge complexes SB-1 and SB-2 correspond to zwitterionic conformations ZNG-1 and ZNG-2, respectively, and both shows OO coordination with carboxylate group. SB-2 is always marginally more favorable over SB-1 for all alkali metal cations. For Li⁺ ion CS-1 and CS-2 are almost equally preferred charge solvated structures and these are about 2.14 and 2.64 kcal mol⁻¹ less stable from SB-2. With an increase in the size of metal ions, these NO coordinated structures become less favorable, on the respective potential energy surfaces. The Li⁺ bound canonical structure, CS-4 does not exist and it is converged to SB-1 at B3LYP/6-31+G(d,p) or 6-311++G(d,p) and M06-2X/6-311+G(2df,p) levels (Table 2 and S4†). However, this Li⁺ bound structure CS-4 is found to be the least stable structure at M06/6-311++G(d,p) and BhandHlyp/6-311++G(d,p) levels of theory. The stability of CS-4 increases with an increase in the size of the metal cations; and it becomes gradually the most preferred canonical structure. Similarly, for Na⁺ ion, charge solvated structures (CS-1 and CS-2) are equally (difference is less than 0.75 kcal mol⁻¹) preferred while CS-3 is the least favored. The stability of Na⁺ bound CS-1 and CS-2 is found to be decreased by 4.92 and 3.67 kcal mol⁻¹, respectively compared to Li⁺ bound structures. The CS-2 type, charge solvated structure is found to be the most stable structure for Gly bound Li⁺ and Na⁺ complexes by about 1.4–3.3 kcal mol⁻¹ over zwitterionic structure.¹⁷

Fig. 6 Schematic representation of the charge solvated and salt bridge structures of NG with alkali metal cations (M⁺ = Li, Na, K, Rb, Cs).

Fig. 7 Optimized charge solvated and salt bridge 3D structures of NG with Na⁺ cation (M06-2X/6-311++G(d,p)).

Table 2 Relative energies (kcal mol⁻¹) of alkali metal cationized charge solvated and salt bridge structures at M06-2X/6-311+G(2df,p) level of theory^ab

Cations	CS-1	CS-2	CS-3	CS-4	CS-5	SB-1	SB-2
a CS-4 of Li^+ cation converged to SB-1.b All CS-5 converged to SB-2.
Li^+	2.14	2.64	12.18	—	—	0.49	0.00
Na^+	7.06	6.31	11.94	10.66	—	0.51	0.00
K^+	8.73	7.69	10.31	7.87	—	0.81	0.00
Rb^+	8.66	7.46	9.04	5.59	—	1.48	0.00
Cs^+	8.59	7.32	8.48	4.52	—	1.85	0.00

---

For the larger cations (K⁺ to Cs⁺) the stability order of charge solvated structures is quite different from the smaller alkali ions (Li⁺ and Na⁺). The structures (CS-1 and CS-2) in which cation is attached to nitrogen and oxygen atoms, become less stable than the structures where cation is bound to the oxygen atoms of carboxylic group (CS-4). For the larger alkali cations, CS-4 is the more preferable among charge solvated structures. Moving from Li⁺ to Cs⁺ cations the relative stability of CS-4 is increasing while the relative stability of CS-1 and CS-2 is decreasing. For example, CS-4 in the presence of Li⁺ cation is the least stable structure by 14.54 kcal mol⁻¹ but in the presence of Cs⁺ cation, it is the most stable structure only by 3.76 kcal mol⁻¹ at M06/6-311++G(d,p) level; it signifies that the stability of CS-4 is enhanced by 10 kcal mol⁻¹. For the K⁺ cation, NO and OO coordinated structures (CS-2 and CS-4) are nearly isoenergetic with each other whereas for Rb⁺ and Cs⁺ cations CS-4 is preferred by about 2–3 kcal mol⁻¹ over CS-2. In the complexes of Gly with larger cations (K⁺ to Cs⁺), CS-4 type charge solvated structure is the global minimum and it is 2–3 kcal mol⁻¹ more stable than salt bridge structure.¹⁷ The coordination preferences (NO vs. OO) of charge solvated structures of NG are identical with Gly bound alkali cation charge solvated structures.¹⁷ Results indicate that alkali cations binding to nonzwitterionic form of NG changes the NO coordination preferences for smaller alkali ions (Li and Na) to OO coordination for larger alkali ions Rb⁺ and Cs⁺. While for K⁺ cation NO and OO coordinated structures are almost isoenergetic with each other.

The stability of SB-1 is almost independent of the nature of alkali metal ions (energy varies only within 1.37 kcal mol⁻¹). Calculations show that NG changes its preferences from charge solvated structure CS-1 for smaller cations to CS-4 for larger alkali cations because of a lower tendency of larger alkali ions for intermolecular charge solvation.²⁴ This indicates that for the complexes of NG with larger alkali ions (low charge densities) not only charge solvation is important but also hydrogen bonding. While in the case of complexes of smaller alkali ions (higher charge densities) only charge solvation is sufficient to stabilize the charge solvated structures. Similar observation have been suggested for alkali bound complexes of Arg.²⁴ In the complexes of NG with alkali metal cations, the energy difference between the most stable nonzwitterionic and zwitterionic forms depends on their cation size, and the stability of zwitterionic complexes decrease with an increase in metal ion size (Fig. 8). In contrast, the Arg–alkali metal complexes were observed to show opposite trends, whose zwitterions stability increases with alkali ions size.^25,61 K⁺ cation forms the most favorable zwitterion with NG, which is about 7.69 kcal mol⁻¹ more stable than canonical form. The relative stability of (NG-M⁺) zwitterions decrease as follows: SB-K⁺ (7.69 kcal mol⁻¹) > SB-Na⁺ (6.31 kcal mol⁻¹) > SB-Rb⁺ (5.59 kcal mol⁻¹) > SB-Cs⁺ (4.52 kcal mol⁻¹) > SB-Li⁺ (2.14 kcal mol⁻¹) (Table 2).

Fig. 8 Energy difference between the charge solvated and salt bridge structures for NG-M⁺ complex, M⁺ = Li, Na, K, Rb and Cs, plotted as a function of metal cation size.

Complexation energy and metal binding affinity. The complexation energy of NG-M⁺ is following the nearly same trend as that of their relative stability (Table 3). The SB-2 has highest complexation energy for any of the cations. The complexation energy of smaller cations indicated that these cations favorably bind to CS-1 and/or CS-2 compared to CS-3 or CS-4 because the former have larger metal binding affinity. For instance, complexation energies for Na⁺ cation binding are −49.10 and −45.50 kcal mol⁻¹ respectively, for CS-1 and CS-4. This shows that smaller cations preferentially bind in NO mode rather than the OO mode in charge solvated structures due to lower binding affinity of smaller cations for CS-4 (OO mode). On the other hand, larger alkali cations have higher complexation energy for CS-4 compared to any other charge solvated structures (e.g. −26.98 and −22.90 kcal mol⁻¹ for Cs⁺ bound CS-4 and CS-1). It implies that larger alkali cations easily coordinated with both oxygen atoms of carboxylic group (OO mode) compared to carbonyl oxygen and central nitrogen atoms (NO mode).

Table 3 Metal binding affinity, conformational penalty and complexation energy (kcal mol⁻¹) of charge solvated and salt bridge structures with alkali metal cations (M06-2X/6-311+G(2df,p))

Cations	CS-1	CS-2	CS-3	CS-4	SB-1	SB-2
	Metal binding affinity (Evertical)
Li^+	−86.00	−79.81	−74.94		−95.09	−90.62
Na^+	−61.17	−58.10	−55.47	−49.06	−75.58	−70.69
K^+	−44.66	−44.23	−42.84	−38.01	−61.79	−56.60
Rb^+	−35.72	−36.66	−35.10	−31.94	−52.66	−47.36
Cs^+	−30.31	−32.08	−30.47	−28.42	−47.68	−42.40
Conformational penalty/deformation energy (Edeformation)
Li^+	14.62	8.92	13.60		22.05	17.09
Na^+	12.06	8.24	11.25	3.56	19.92	14.53
K^+	9.80	8.34	9.57	2.30	19.01	13.01
Rb^+	8.58	8.33	8.35	1.74	18.35	11.57
Cs^+	7.41	7.91	7.46	1.45	18.04	10.91
Complexation energy
Li^+	−71.38	−70.88	−61.34		−73.04	−73.52
Na^+	−49.10	−49.85	−44.22	−45.50	−55.66	−56.16
K^+	−34.86	−35.89	−33.27	−35.71	−42.77	−43.58
Rb^+	−27.13	−28.33	−26.74	−30.20	−34.31	−35.79
Cs^+	−22.90	−24.17	−23.01	−26.98	−29.64	−31.49

---

E_deformation and E_vertical are highest for the smallest Li⁺ cation bound complexes and consistently decreasing with the size of the metal ion, therefore, these are lowest for Cs⁺ bound complexes. Table 3 indicates that conformational penalty is usually higher for the salt bridge structures compared to charge solvated structures. This higher penalty may be attributed due to the proton transfer from the acidic center to basic guanidino group. Similarly, the metal binding affinity of salt bridge structures is higher than charge solvated structures. As per E_vertical data, CS-1 (and CS-2) is expected to be more preferable while CS-4 is least preferred among CS structures. However, upon considering conformational penalty along with E_vertical, CS-1 (or CS-2) was observed to be preferred in smaller (Li⁺, Na⁺) cations, while CS-4 in larger (K⁺–Cs⁺) alkali metal cations. This reversal of trend may have arisen due to higher conformational penalty (7.41–14.62 kcal mol⁻¹) of CS-1 as compared to CS-4, where no such significant conformational penalty is observed (<3.56 kcal mol⁻¹). The SB-2 is favored over the all structures of cation bound complexes however; its binding affinity is not larger than SB-1. The higher binding affinity of SB-1 than SB-2 is offset by the higher conformational penalty of SB-1 over SB-2. The conformational penalty for CS-1 and CS-3 is almost same therefore, the difference in E_vertical directly reflecting the relative stability of them.

Alkaline earth metal cation complexation. The alkaline earth metal cationized charge solvated and salt bridge structures of NG are illustrated in Fig. 9, and their relative energies are given in Table 4. Optimized 3D structures are given in Fig. 10 for Mg²⁺cation. All the complexes are optimized using B3LYP/6-31+G(d,p), B3LYP/6-311++G(d,p), BHandHLYP/6-311++G(d,p), M06/6-311++G(d,p) and M06-2X/6-311+G(2df,p) levels of theory. On the basis of chemical intuition, six charge solvated and two salt bridge structures may be possible, however, on the potential energy surface only NO coordinated structures are found for all metal cations. The probable OO coordinated CS-5 and CS-6 structures are converted to salt bridge structures SB-1 and SB-2, respectively in the presence of alkaline earth metal cations. Like alkali cations, in CS-1 and CS-2, divalent cations are chelated to guanidine nitrogen and carbonyl oxygen atoms. In the charge solvated structures CS-3 and CS-4, cations chelated with two nitrogen atoms of guanidine and carbonyl oxygen through NNO tri-coordination. Like alkali cation complexes, salt bridge structures of alkaline earth cations are the most stable. SB-1 is the lowest energy structure for all metal cations except for Be²⁺ ion; SB-2 is marginally higher in energy (by 1.24–2.74 kcal mol⁻¹) over SB-1.

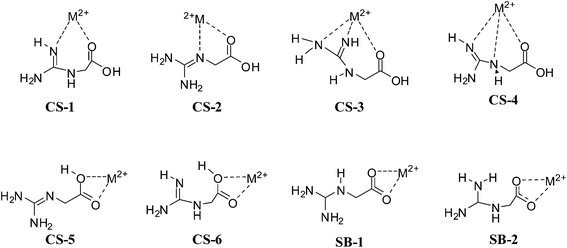Fig. 9 Schematic representation of the charge solvated and salt bridge structures of NG with alkaline earth cations (M²⁺ = Be, Mg, Ca, Sr, Ba).

Table 4 Relative energies (kcal mol⁻¹) of charge solvated and salt bridge structures of NG with alkaline earth cations (M06-2X/6-311+G(2df,p))^a

Cations	CS-1	CS-2	CS-3	CS-4	CS-5	CS-6	SB-1	SB-2
a CS-5 and CS-6 of all cations converged to SB-1 and SB-2, respectively.
Be^2+	−25.52	−13.18	6.81	−24.64	—	—	0.00	1.24
Mg^2+	1.50	8.18	18.40	−1.35	—	—	0.00	2.33
Ca^2+	13.75	12.31	21.30	11.47	—	—	0.00	2.83
Sr^2+	15.28	12.51	19.91	13.37	—	—	0.00	2.79
Ba^2+	17.11	14.25	19.59	15.81	—	—	0.00	2.74

---

Fig. 10 Optimized charge solvated and salt bridge structures of NG with Mg²⁺ cation (M06-2X/6-311++G(d,p)).

For Be²⁺ cation, the charge solvated structures are highly favored over salt bridge structures except CS-3. CS-1 and CS-4 are more stable by −25.52 and −24.64 kcal mol⁻¹, respectively over SB-1. CS-2 is the third preferred structure over salt bridge structures. For Mg²⁺ cation CS-1 and CS-4 are more favorable than the other charge solvated structures. In addition, the relative stability of SB-1 lies between CS-1 and CS-4 (±1.50 kcal mol⁻¹). This low energy difference between the charge solvated and salt bridge structures of Mg²⁺ cation indicates that the transition from the canonical structure to zwitterionic form starts with Mg²⁺cation. In the complexes of divalent cations (Ca²⁺, Sr²⁺ and Ba²⁺) CS-2 and CS-4 are lower energy charge solvated structures and the energy difference found between them is not significant (<1.5 kcal mol⁻¹).

The relative stabilities of all charge solvated structures gradually decrease with an increase in the size of cations (Fig. 11). In contrast, the stability of the most favored charge solvated structure (CS-4) of alkali cations is increased as moving down in an alkali cation group. It is interesting to note that the energy difference between the lowest energy salt bridge and charge solvated structures is decreased for alkali cations, while increased for alkaline earth cations upon moving down in their corresponding group. This reveals that NG complexation with alkaline earth metal cation leads to the lowest energy canonical form with Be²⁺, in addition, the canonical and zwitterionic forms are of lower energy difference for Mg²⁺ ion. Williams and coworkers¹⁸ reported almost similar pattern for Gly complexes with alkaline earth cations where Gly–M²⁺ complex contains the charge solvated structure for Be²⁺ and zwitterionic forms with Mg²⁺, Ca²⁺, Sr²⁺ and Ba²⁺ cations. In contrast, same group observed identical pattern for complexation of Arg with alkali cations where Arg exist in the canonical form for Li⁺, zwitterionic from for K⁺, Rb⁺, Cs⁺ and in both forms together for Na⁺.⁶¹ The stability of the salt bridge structure compared to charge solvated structure, increases with an increase in alkaline earth metal cations size except Be²⁺cation. Similarly, the stability of salt bridge structures of alkaline earth metal cations with Gly¹⁸ and Arg^26,61 increase with an increase in metal cation size.

Fig. 11 Energy difference between the charge solvated and salt bridge structures for NG-M²⁺ complex, M²⁺ = Be, Mg, Ca, Sr, Ba, plotted as a function of metal cation size.

Be²⁺ ion has highest metal binding affinity for charge solvated structures (CS-1 and CS-4) compared to salt bridge structures (Table 5), therefore, these structures are favoured over salt bridge structures. Alkaline earth cations bound conformations of NG, in complexes are not close to global minimum isomers (NG-1/NG-2) hence these have very high conformational penalty. E_vertical and E_deformation are continuously decreasing with an increase in the size of metal cations. The relative energy profile of alkaline earth cations complexes is completely mirrored by complexation energy.

Table 5 Metal binding affinity, conformational penalty and complexation energy (kcal mol⁻¹) of charge solvated and salt bridge structures with alkaline earth metal cations (M06-2X/6-311+G(2df,p))

Cations	CS-1	CS-2	CS-3	CS-4	SB-1	SB-2
	Metal binding affinity (Evertical)
Be^2+	−374.61	−358.86	−352.97	−385.48	−363.05	−366.69
Mg^2+	−228.44	−216.84	−214.23	−238.24	−237.47	−232.98
Ca^2+	−164.88	−173.08	−157.08	−173.81	−185.65	−180.28
Sr^2+	−126.80	−134.28	−120.75	−135.37	−147.92	−141.39
Ba^2+	−109.19	−114.77	−104.31	−117.08	−131.67	−125.39
Conformational penalty/deformation energy (Edeformation)
Be^2+	33.28	29.86	43.96	45.02	47.23	52.11
Mg^2+	24.40	19.49	27.09	31.36	31.93	29.78
Ca^2+	21.57	28.32	21.33	28.22	28.59	26.05
Sr^2+	19.35	24.05	17.93	26.01	25.18	21.45
Ba^2+	18.48	21.20	16.08	25.07	23.86	20.31
Complexation energy
Be^2+	−341.33	−329.00	−309.01	−340.46	−315.82	−314.58
Mg^2+	−204.04	−197.35	−187.14	−206.88	−205.54	−203.20
Ca^2+	−143.31	−144.75	−135.76	−145.59	−157.06	−154.23
Sr^2+	−107.45	−110.22	−102.82	−109.36	−122.73	−119.94
Ba^2+	−90.71	−93.57	−88.22	−92.01	−107.82	−105.08

---

Conclusions

NG is a precursor of CR, which plays an important role in ATP balance in our body. Quantum chemical calculations have been performed using B3LYP, BHandHLYP, MP2 M06 and M06-2X methods, on NG to understand the conformational and zwitterionic preferences under the influence of metal ion and water coordination. Computational analysis indicated that conformers and zwitterions of NG are sensitive to its environment. In the gas phase canonical conformations, NG-1 and NG-2 are isoenergetic, and are preferred over zwitterion (ZNG-1) by about 14–15 kcal mol⁻¹. In addition, alternative zwitterion, ZNG-2 is not found in the gas phase at B3LYP, BHandHLYP, MP2 and M06-2X methods. Large difference in the zwitterionic preferences in NG (∼15 kcal mol⁻¹) vs. in Arg (∼3 kcal mol⁻¹) in the gas phase can be attributed to the difference in the intramolecular solvation by H-bond observed in Arg.

In the presence of one water molecule, the energy difference between canonical and zwitterionic forms of NG is reduced to 3.64 kcal mol⁻¹ from a 15 kcal mol⁻¹ (in bare forms). Further, in the presences of two water molecules both forms are very close in energy and the zwitterionic NG clearly dominates canonical form in the three water clusters. In larger water clusters (4–6), several zwitterionic structures are found to be highly stable over canonical structures. This indicates that in microsolvated condition, zwitterionic stability of NG is similar to that of Arg while in the gas phase it is near to Gly (∼15 kcal mol⁻¹).

The alkali metal cationized the charge solvated structure CS-5 (OO coordinated) is not stable on the potential energy surface and the other OO coordinated the lowest energy structure CS-4 lies 4–15 kcal mol⁻¹ above the salt bridge structures. The relative stability of the charge solvated structure CS-4 of alkali cations increases with an increase in size of metal ions. The complexation energy of NG with alkali metal ions is decreasing with an increase in size of the metal ions and it depends on the metal binding affinity and conformational penalty. Smaller cations (Li⁺, Na⁺) are preferentially coordinated in NO geometry rather than OO geometry in charge solvated structures due to their higher metal binding affinity for NO coordination. In alkali cationized NG structures, K⁺ ions form the most stable zwitterionic structure, which is about 7.7 kcal mol⁻¹ more stable than lowest energy canonical structure.

On the other hand, for the alkaline earth cationized NG both the charge solvated structures with OO coordination (CS-5 and CS-6) are not found on the potential energy surface. While for these cations, only NO coordinated charge solvated structures are established. The salt bridge structures are about 1–14 kcal mol⁻¹ more stable than the charge solvated structures for all metal ions except Be²⁺ ion. For Be²⁺ ion two charge solvated structures (CS-1 and CS-4) are 25–26 kcal mol⁻¹ more stable than salt bridge structure, while for Mg²⁺ ion both of these structures are competitive. In contrast to alkali cations the charge solvated structure (CS-4), the stability of all charge solvated structures of alkaline earth metal cations decreases with an increase of metal ion in size.

Acknowledgements

Authors are thankful to Council of Scientific and Industrial Research (CSIR), New Delhi and NIPER, S. A. S. Nagar for providing financial support.

References

1. K. Bloch and R. Schoenheimer, J. Biol. Chem., 1941, 138, 167.
2. M. Wyss and R. Kaddurah-Daouk, Physiol. Rev., 2000, 80, 1107.
3. M. Takeda, I. Kiyatake, H. Koide, K. Y. Jung and H. Endou, Eur. J. Clin. Chem. Clin. Biochem., 1992, 30, 325.
4. L. S. Almeida, N. M. Verhoeven, B. Roos, C. Valongo, M. L. Cardoso, L. Vilarinho, G. S. Salomons and C. Jakobs, Mol. Genet. Metab., 2004, 82, 214.
5. C. Carducci, M. Birarelli, V. Leuzzi, R. Battini, G. Cioni and I. Antonozzi, Clin. Chem., 2002, 48, 1772.
6. S. Mercimek-Mahmutoglu, S. Stoeckler-Ipsiroglu, A. Adami, R. Appleton, H. C. Araujo, M. Duran, R. Ensenauer, E. Fernandez-Alvarez, P. Garcia, C. Grolik, C. B. Item, V. Leuzzi, I. Marquardt, A. Muhl, R. A. Saelke-Kellermann, G. S. Salomons, A. Schulze, R. Surtees, M. S. van der Knaap, R. Vasconcelos, N. M. Verhoeven, L. Vilarinho, E. Wilichowski and C. Jakobs, Neurology, 2006, 67, 480.
7. A. Neu, H. Neuhoff, G. Trube, S. Fehr, K. Ullrich, J. Roeper and D. Isbrandt, Neurobiol. Dis., 2002, 11, 298.
8. J. Verhelst, J. Berwaerts, B. Marescau, R. Abs, H. Neels, C. Mahler and P. P. De Deyn, Metabolism, 1997, 46, 1063.
9. M. Kuroda, Nephron, 1993, 65, 605.
10. A. I. Zugno, R. Franzon, F. Chiarani, C. S. Bavaresco, C. M. Wannmacher, M. Wajner and A. T. Wyse, Int. J. Dev. Neurosci., 2004, 22, 191.
11. J. H. Jensen and M. S. Gordon, J. Am. Chem. Soc., 1995, 117, 8159.
12. D. Yu, D. A. Armstrong and A. Rauk, Can. J. Chem., 1992, 70, 1762.
13. E. Kassab, J. Langlet, E. Evleth and Y. Akacem, J. Mol. Struct.: THEOCHEM, 2000, 531, 267.
14. S. M. Bachrach, J. Phys. Chem. A, 2008, 112, 3722.
15. M. Gutowski, P. Skurski and J. Simons, J. Am. Chem. Soc., 2000, 122, 10159.
16. T. Wyttenbach, M. Witt and M. T. Bowers, J. Am. Chem. Soc., 2000, 122, 3458.
17. S. Hoyau and G. Ohanessian, Chem.–Eur. J., 1998, 4, 1561.
18. E. F. Strittmatter, A. S. Lemoff and E. R. Williams, J. Phys. Chem. A, 2000, 104, 9793.
19. Z. B. Maksic and B. Kovacevic, J. Chem. Soc., Perkin Trans. 2, 1999, 2623.
20. S. Ling, W. Yu, Z. Huang, Z. Lin, M. Haranczyk and M. Gutowski, J. Phys. Chem. A, 2006, 110, 12282.
21. J. Rak, P. Skurski, J. Simons and M. Gutowski, J. Am. Chem. Soc., 2001, 123, 11695.
22. S. Im, S. W. Jang, S. Lee, Y. Lee and B. Kim, J. Phys. Chem. A, 2008, 112, 9767.
23. P. Skurski, J. Rak, J. Simons and M. Gutowski, J. Am. Chem. Soc., 2001, 123, 11073.
24. B. A. Cerda and C. Wesdemiotis, Analyst, 2000, 125, 657.
25. R. A. Jockusch, W. D. Price and E. R. Williams, J. Phys. Chem. A, 1999, 103, 9266.
26. M. F. Bush, J. Oomens, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2008, 130, 6463.
27. M. Remko and B. M. Rode, J. Phys. Chem. A, 2006, 110, 1960.
28. A. G. Harrison, Mass Spectrom. Rev., 1997, 16, 201.
29. J. L. de Miranda and J. Felcman, Synth. React. Inorg. Met.-Org. Chem., 2001, 31, 873.
30. T. Wyttenbach, M. Witt and M. T. Bowers, Int. J. Mass Spectrom., 1999, 182–183, 243.
31. J. M. Ramos, O. Versiane, J. Felcman and C. A. Téllez S, Spectrochim. Acta, Part A, 2009, 72, 182.
32. O. Versiane, B. L. Rodrigues, J. L. de Miranda, J. M. Ramos, C. A. Téllez S and J. Felcman, Polyhedron, 2007, 26, 4363.
33. J. L. de Miranda, J. da Silva Coelho, L. C. de Moura, M. H. Herbst, B. A. C. Horta, R. B. de Alencastro and M. G. Albuquerque, Polyhedron, 2008, 27, 2386.
34. J. B. Foresman and A. E. Frisch, Exploring Chemistry with Electronic Structure Methods, Gaussian, Inc., Pittsburgh, PA, 1995.
35. W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, Wiley, New York, 1985.
36. R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989.
37. J. A. Pople and D. L. Beveridge, Approximate Molecular Orbital Theory, McGraw-Hill Book, New York, 1970.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision C.02, Gaussian, Inc., Wallingford CT, 2009.
39. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
40. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244.
41. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
42. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
43. R. Krishnan, M. J. Frisch and J. A. Pople, J. Chem. Phys., 1980, 72, 4244.
44. Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
45. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
46. B. J. Lynch, Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2003, 107, 1384.
47. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995.
48. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378.
49. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
50. G. Yang, Y. Zu, C. Liu, Y. Fu and L. Zhou, J. Phys. Chem. B, 2008, 112, 7104.
51. D.-S. Ahn, S.-W. Park, I.-S. Jeon, M.-K. Lee, N.-H. Kim, Y.-H. Han and S. Lee, J. Phys. Chem. B, 2003, 107, 14109.
52. S. M. Bachrach, T. T. Nguyen and D. W. Demoin, J. Phys. Chem. A, 2009, 113, 6172.
53. D. L. Crittenden, M. Chebib and M. J. Jordan, J. Phys. Chem. A, 2004, 108, 203.
54. D. K. Dhaked and P. V. Bharatam, J. Phys. Chem. A, 2014, 118, 187.
55. Z. P. Nathavad, S. Bhatia, D. K. Dhaked and P. V. Bharatam, Comput. Theor. Chem., 2013, 1023, 51.
56. D. K. Dhaked and P. V. Bharatam, RSC Adv., 2013, 3, 25268.
57. J.-Y. Kim, Y. Lee and S. Lee, Chem. Phys. Lett., 2014, 608, 177–185.
58. T. K. Hwang, G. Y. Eom, M. S. Choi, S. W. Jang, J. Y. Kim, S. Lee, Y. Lee and B. Kim, J. Phys. Chem. B, 2011, 115, 10147.
59. M. N. Blom, I. Compagnon, N. C. Polfer, G. Helden, G. Meijer, S. Suhai, B. Paizs and J. Oomens, J. Phys. Chem. A, 2007, 111, 7309.
60. K. Chuchev and J. J. BelBruno, J. Mol. Struct.: THEOCHEM, 2008, 850, 111.
61. M. F. Bush, J. T. O'Brien, J. S. Prell, R. J. Saykally and E. R. Williams, J. Am. Chem. Soc., 2007, 129, 1612.
62. P. B. Armentrout, B. Yang and M. T. Rodgers, J. Phys. Chem. B, 2013, 117, 3771.
63. R. C. Dunbar, J. D. Steill, N. C. Polfer and J. Oomens, J. Phys. Chem. A, 2009, 113, 845.
64. M. K. Drayß, P. Armentrout, J. Oomens and M. Schäfer, Int. J. Mass Spectrom., 2010, 297, 18.
65. M. Cametti, M. Nissinen, A. Dalla Cort, L. Mandolini and K. Rissanen, J. Am. Chem. Soc., 2005, 127, 3831.
66. T. Wyttenbach, D. Liu and M. T. Bowers, J. Am. Chem. Soc., 2008, 130, 5993.
67. S. K. Kim, J. L. Sessler, D. E. Gross, C. H. Lee, J. S. Kim, V. M. Lynch, L. H. Delmau and B. P. Hay, J. Am. Chem. Soc., 2010, 132, 5827.
68. F. Jensen, J. Am. Chem. Soc., 1992, 114, 9533.

---

Footnote

† Electronic supplementary information (ESI) available: The alternative microsolvated geometries and their relative energies as well as the relative energies data of metal cationized salt bridges and charge solvated structures is given in ESI. In addition, Cartesian coordinates of the optimized structures are also given. See DOI: 10.1039/c4ra06079b

---