Theoretical studies on the dynamics of DNA fragment translocation through multilayer graphene nanopores

Abstract

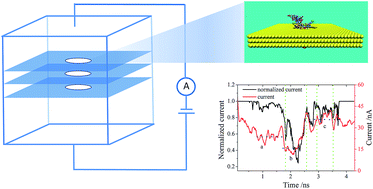
Motivated by several potential advantages over common sequencing technologies, solid-state nanopores, in particular graphene nanopores, have recently been extensively explored as biosensor materials for DNA sequencing. Studies carried out on monolayer graphene nanopores aiming at single-base resolution have recently been extended to multilayer graphene (MLG) films, indicating that MLG nanopores are superior to their monolayer counterparts for DNA sequencing. However, the underlying dynamics and current change in the DNA translocation to thread MLG nanopores remain poorly understood. In this paper, we report a molecular dynamics study of DNA passing through graphene nanopores of different layers. We show that the DNA translocation time could be extended by increasing the graphene layers up to a moderate number (7) under a high electric field and that the current in DNA translocation undergoes a stepwise change upon DNA going through an MLG nanopore. A model is built to account for the relationship between the current change and the unoccupied volume of the MLG nanopore. We demonstrate that the dynamics of DNA translocation depends specifically on the interaction of nucleotides with the graphene sheet. Thus, our study indicates that the resolution of DNA detection could be improved by increasing the number of graphene layers in a certain range and by modifying the surface of the graphene nanopores.

---

1. Introduction

In the presence of an external bias voltage, a DNA or RNA molecule dispersed in a salt solution can be driven through a nanopore, thereby interrupting the flow of the salt ions and triggering a detectable change of the ion current which can be used to probe the identity of the bases in the molecule.^1,2 DNA sequencing with nanopores, such as solid-state^3–8 or biological nanopores,^9–11 is believed to be superior to other sequencing technologies and has experienced an exceptionally rapid development in recent years. For example, by using a mutant MspA nanopore and phi29 DNA polymerase, Manrao et al. were able to read DNA at single-nucleotide resolution.¹²

An advantage of using biological nanopores is that they can be chemically engineered through advanced molecular biology techniques. However, the lipid membrane to fix the biological nanopores is delicately sensitive to temperature, pH and salt concentration, which makes biological nanopore difficult to control their stability. In contrast, with established technologies, very stable and functionally useful solid-state nanopores can be fabricated using silicon nitride,^13–15 silicon oxide^16,17 or metal oxide.¹⁸ Thanks to the robustness and the ability to tune the size and shape of the nanopores used, different types of nanopore have been used to sequence DNA.⁵ However, solid-state nanopores are typically tens of nanometers in thickness which makes it difficult to sequence DNA with low-noise detection.¹⁹

Recently, solid-state nanopores fabricated from graphene sheets²⁰ have attracted intensive interest due to the unique properties of graphene.^21–24 Reading a DNA molecule at single-nucleotide resolution with a monolayer graphene nanopore has though been hampered by the fast translocation speed of the DNA.²⁵ Many theoretical and experimental studies have been carried out to solve this problem, such as those studying decreasing temperature, decreasing applied voltage or increasing solvent viscosity.^26–29 However, such methods are unable to change the translocation dynamics of DNA through a nanopore. Recently, multilayer graphene (MLG) films of less than 10 layers have been fabricated and tested in this respect, and their properties were found to be superior to those of monolayer graphene sheets.³⁰ Kim et al. pointed out the few layer graphene possessed low noise ratio as compared to single layer graphene.³¹ Although DNA sequencing with MLG nanopores has been investigated intensively,³² the dynamics and details of the sequencing process remain unclear.

The aim of our work is to apply Molecular Dynamics (MD) simulations to study the atomistic details of a DNA molecule translocation through a nanopore. MD simulations have been successfully applied to the study of DNA translocation driven by electric fields.^33–36 In this work, we carried out MD simulations to investigate DNA translocation through MLG nanopores. Due to its simplicity, poly(A-T)₄₅ was used as a model DNA fragment. We demonstrate that the translocation time can be extended by increasing the graphene layers to a certain range. By studying the current change of the DNA fragment going through the MLG nanopores, we built a model to explore the relationship between the unoccupied volume of the nanopore and the signal current and investigated the relationship between the translocation speed of the nucleotides and the interaction of the nucleotides with the graphene sheets.

2. Computational method

2.1. System setup

Table 1 lists the systems studied in this work. For each system, an MLG sheet was placed in the x–y plane with its center of mass in the origin (0, 0, 0) of a Cartesian coordinate system. A nanopore was constructed by deleting the atoms with their coordinates satisfying x² + y² < D², where D is the radius of the graphene nanopore and was set to 1.5 nm, the bond length is 1.42 Å in multilayer graphene sheet, and the separation distance is 3.4 Å between graphene sheets. Poly(A-T)₄₅ was constructed by using the Hyperchem software (Version 7.0, Hypercube, Inc). The nanopore and poly(A-T)₄₅ were placed in a box and solvated with 45340 TIP3P water molecules.³⁷ The TIP3P water model is compatible with the CHARMM force field which is used in this work to model the DNA fragment. The system then underwent a 10 000-step energy minimization. Thereafter, KCl was added to make its concentration equal to 1.0 M as in experiment³⁸ by replacing the water molecules randomly. The system was then subject to a 200 000-step energy minimization. The length of the simulation box is 90 Å in the x and y directions in all the simulations, while in the z direction the box length changes with the number of layers of the graphene nanopore, and the box length is varied from 250 Å to 270 Å in z direction in different simulations with different graphene layers. Fig. 1 shows the initial setup of the system with poly(A-T)₄₅ and a three-layer graphene nanopore.

Table 1 Systems studied^a

	Number of atoms	Number of layers	Temperature (K)	Voltage (mV nm^−1)	DNA fragment	Simulation time (ns)
a The concentration of KCl is 1.0 M in all the simulations.
Sim1	134 235	1	298	100		10
Sim2	134 543	3	298	100		10
Sim3	134 257	5	298	100		10
Sim4	134 387	7	298	100		10
Sim5	134 556	9	298	100		10
SimD1	175 336	1	298	100	Poly(A-T)45	10
SimD2	192 232	3	298	100	Poly(A-T)45	5
SimD3	193 213	5	298	100	Poly(A-T)45	10
SimD4	195 433	7	298	100	Poly(A-T)45	10
SimD5	201 775	9	298	100	Poly(A-T)45	20
SimN1	12 982	1	298		Poly(dA)5	20
SimN2	13 282	1	298		Poly(dT)5	20
SimN3	12 793	1	298		Poly(dC)5	20
SimN4	12 874	1	298		Poly(dG)5	20
SimV1	175 336	1	298	30	Poly(A-T)45	50
SimV2	192 232	3	298	30	Poly(A-T)45	50
SimV3	193 213	5	298	30	Poly(A-T)45	50
SimV4	195 433	7	298	30	Poly(A-T)45	50
SimV5	201 775	9	298	30	Poly(A-T)45	50

---

Fig. 1 Initial setup of the system with poly(A-T)₄₅ and a three-layer graphene nanopore. The DNA fragment is placed above the top of the graphene nanopore, as shown by the vdW (van der Waals) model. K⁺ (pink) and Cl⁻ (green) ions are shown by the CPK (Corey–Pauling–Kortum) model. Water molecules are not shown for clarity.

All MD simulations were performed three times by the Gromacs program³⁹ with a time step of 2.0 fs, and all bonds that involve H-atoms were fixed. The density in all the simulations varied from 1.051 to 1.054 g cm⁻³. The DNA fragment and KCl were modeled by the Charmm27 force field.⁴⁰ All the carbon atoms in the graphene sheets were set to be neutral. The Lennard-Jones parameters of the graphene carbon atoms were σ_CC = 0.385 nm and ε_CC = −0.439 kJ mol⁻¹.^36,41 Periodic boundary condition was used in all directions. The cutoff for the non-bonded van der Waals interaction was set by a switching function starting at 1.0 nm and reaching zero at 1.2 nm. The Langevin method was employed to keep the simulation temperature at 298.0 K, and the pressure was set to 101.3 kPa in all directions. The particle mesh Ewald summation was used to recover the long range electrostatic interaction, with a cutoff of 1.3 nm for the separation of the direct and reciprocal space summation. A bias voltage of 100 mV nm⁻¹ was applied to drive the ions and the DNA fragment passing through the nanopores in all the simulations. This bias voltage has the same magnitude as that used in our previous work.³⁶

2.2. Analysis method

To describe the blockade current of a DNA molecule through a nanopore and to explain the phenomenon, the time-dependent ionic current I(t) was calculated as,²⁶where L_z is the length of the system in the z-direction, z_i(t) is the z coordinate of atom i at time t, Δt is set to 10.0 ps, N is the total number of atoms, including those of the DNA and ions, and q_i is the charge of atom i, respectively. The interaction of a nucleotide with each graphene layer was calculated by:

E_int = E_gra + E_nuc − E_gra+nuc (2)

where E_int is the interaction of the nucleotide with the graphene layer, E_gra, E_nuc, E_gra+nuc are potential energies of graphene layer, nucleotide, and graphene with nucleotide, respectively.

3. Results and discussion

3.1. Open nanopore resistance

In our previous work, the relationship between the diameter of a nanopore and its open nanopore resistance was investigated.⁴² Here, the resistance (Res) of the nanopores was evaluated, with the diameter of the nanopores set to 3 nm. A series of MD simulations were performed with the number of graphene layers varying from 1 to 9 under the same KCl concentration (1.0 M) as used in experiments.³⁸ Due to the applied external electric field, K⁺ and Cl⁻ ions were driven to move in opposite directions and the average ionic current 〈I〉 was calculated from eqn (1). The slope of the V/〈I〉 curve was determined as the resistance of a nanopore. Based on the experiment data,²⁵ the resistance on diameter 3 nm monolayer graphene nanopore should be 273.02 MΩ, and it is 38.2 MΩ in our simulation. This indicates that the pore resistance in our simulations is lower than the experimental results. One reason is that the voltage we used is larger than that in experiment, because a low voltage similar to those used in experiment could require a simulation time too long to be practical with our computational resources. Another one is the charge distribution of graphene nanopore is not considered in the simulations, and the force field to describe the interaction of ions and graphene should be improved as mentioned in others work.²⁶ We note here that the thickness of a graphene sheet is directly proportional to the number of graphene layers, which is defined as L. As plotted in Fig. 2, the resistance of the graphene nanopores depends closely on the number of graphene layers, which can be expressed as Res ∼ L. This reflects that the open nanopore resistance of a graphene sheet is also directly proportional to its thickness and the detected current accordingly decreases with the increase of graphene layers. The relationship between the current and the layers of graphene nanopores was also discussed by Lv et al.³² They demonstrated that the ionic current is sensitive to the number of graphene layers, which is in accordance with our result in this work. Because it is difficult to control the thickness of a graphene sheet experimentally, the dependence of the resistance of the graphene sheet on its thickness remains unclear. Here, the relationship between the open nanopore resistance and the thickness was explored qualitatively.

Fig. 2 Change of the open nanopore resistance with the number of graphene layers.

The movement of K⁺ and Cl⁻ ions under the applied field contributes to the measured currents. For Sim2, the contributions of K⁺ and Cl⁻ ions to the current were found to be almost the same (see Fig. 3A). To interpret the phenomenon more deeply, the mean square displacements (MSDs) of K⁺ and Cl⁻ ions in the Z direction of the Cartesian coordinate system, i.e. in the direction of the applied field, were calculated. As shown in Fig. 3B, the MSDs of the two ions in the same simulation time are almost the same.

Fig. 3 (A) Contributions of K⁺ and Cl⁻ to the current in Sim2. (B) MSDs of K⁺ and Cl⁻ in Sim2.

3.2. Effect of the number of graphene layers

Fig. 4 shows the change of the current with the DNA fragment passing through the graphene nanopores of 1, 3, 5, 7, and 9 layers. As seen in the figure, the translocation time is about 0.6 ± 0.2, 1.9 ± 0.8, 3.6 ± 0.9, and 5.1 ± 1.2 ns for the nanopores of 1, 3, 5, and 7 layers, respectively, and the translocation time for 45bp in our simulation is much faster than that in the experiment.²⁵ One reason is the applied voltage is 100 mV nm⁻¹, and the total voltage is 2.5 V, which is much larger than that in experiment. The other reason is the force field used here could not describe the charge distribution of graphene nanopore, which should be improved. Compared with the monolayer graphene sheet, the translocation time was clearly prolonged. This implies that increasing the number of graphene layers could increase the translocation time. One of the major challenges in applying a graphene nanopore to detect a DNA molecule is to reduce the speed at which the DNA molecule passes through the nanopore.⁴³ Our results thus suggest that the translocation time of the DNA fragment can be greatly extended by using MLG nanopores. However, if the number of graphene layers grows large, for example more than 10 (ref. 30 and 44) the electronic structure of a graphene nanopore approaches to the 3D limit of graphite⁴⁵ and can influence the electric properties of the graphene nanopore and produce high noise in the DNA sequencing. Therefore, the number of graphene layers should be less than 10. As we can see from Fig. 4, the translocation time is almost directly proportional to the number of graphene layers if the number varies from 1, 3, 5 and 7, while the translocation time through the 9-layer nanopore becomes very short. As reported by others, the longer a carbon nanotube, the deeper the potential well in the tube, and accordingly a protein can be spontaneously encapsulated into a longer carbon nanotube.^46,47 This is also the case for a nanopore: with the increase of the thickness of a nanopore, the potential well in the nanopore becomes deep. Thus, increasing the number of graphene layers also means deepening the potential well in the nanopore, leading to that the DNA quickly threads to the nanopore. However, the DNA translocation time is not related to the nanopore thickness in the experiment.²⁵ The main reason is the difference of the electric fields applied in the experiments and simulations. With a lower electric field applied in the experiments, the translocation time is greatly extended. As seen in Fig. 4G, the translocation time of poly(A-T)₄₅ through the graphene nanopores of different layers is independent of the number of layers under a low electric field (30 mV nm⁻¹). Under such a low electric field, the driving force for the DNA fragment to pass through a nanopore is very small, while the interaction of the graphene nanopore with the DNA fragment governs the translocation time since the DNA fragment tends to adsorb onto the graphene nanopore. The sticking time and trapping time in the graphene nanopore are so long that the effect of the graphene nanopore thickness on the translocation time is hardly observable. Thus, the translocation time is not related to the number of graphene nanopore layers in the experiment. However, the sticking and trapping times are very short under a high electric field since the driving force is very large. This means that the effect of the graphene nanopore thickness on the translocation time is very important under a high electric field (100 mV nm⁻¹) (see Fig. 4F). Thus, the translocation time is related to the graphene nanopore thickness under a high electric field but not a low electric field. To increase the translocation time and decrease the translocation speed of a DNA molecule, the number of graphene layers should be increased but not exceed a certain number, which is 7 according to our calculations. The average current decreases with the increase of the number of graphene layers since the nanopore resistance is directly proportional to the number of graphene layers.

Fig. 4 Change of the currents with the time for the DNA fragment translocation through graphene nanopores of 1-layer (A), 3-layer (B), 5-layer (C), 7-layer (D) and 9-layer (E) under 100 mV nm⁻¹ electric field, respectively. Δt represents the translocation time for poly(A-T)₄₅ to pass through the nanopores. The blue dashed line in (C) corresponds to the current change with poly(A-T)₄₅ translocation through the nanopore. EXIT means that all the residues of poly(A-T)₄₅ are outside of the nanopore and IN indicates that some segments of poly(A-T)₄₅ are passing through the nanopore. Change of the translocation time with the number of graphene layers under electric fields of 100 mV nm⁻¹ (F) and 30 mV nm⁻¹ (G), respectively.

As shown by the blue dashed line in Fig. 4C, the current undergoes a stepwise change upon the DNA fragment passing through an MLG nanopore. In the first step, the current is ca. 22.5 nA, which is the open ionic current corresponding to that all the residues of poly(A-T)₄₅ are outside of the nanopore. In the second step, the current is ca. 15.1 nA, which is the blocked current corresponding to that one layer of the nanopore is occupied by poly(A-T)₄₅. In the third step, the blocked current becomes ca. 12.3 nA when 2–3 layers of the nanopore are occupied by poly(A-T)₄₅. In the fourth step, the blocked current is ca. 7.6 nA when all the layers of the nanopore are occupied by poly(A-T)₄₅. In the last step, the current recovers to ca. 22.5 nA since all the residues of poly(A-T)₄₅ are outside of the nanopore. The impact of thermal noise on DNA sequencing has been studied by Lv's group⁴⁸ with single-layer rigid or flexible graphene nanopores. It seems that freezing the carbon atoms of a graphene nanopore has essentially no effect on the impact of thermal noise. The impact of thermal noise on multilayer graphene nanopores will be the potential goal of further studies.

3.3. The theoretical model

Here, we take the 3-layer graphene nanopore as an example to explore the dependence of the current on the unoccupied volume of the nanopore. First, only those DNA atoms with the distance to the nanopore less than |z| are considered to influence the movement of ions to pass through the nanopore as described in the previous work.³⁶ The z parameter (|z| ≤ 1.2 nm) depends on the cutoff for the non-bonded van der Waals interaction used in the simulation. As shown in Fig. 5A and B, the captured atoms of poly(A-T)₄₅ occupy the nanopore and prevent the ions from passing through it. To calculate the normalized current, a nanopore was considered as a cylinder and was divided into N parts of equal length in the Z direction. As shown in Fig. S1,† we found that the model normalized current is independent of N when N is larger than 10 for the 3-layer graphene nanopore (see ESI†). Here, the 3-layer graphene nanopore was divided into 12 parts, with each part being 0.6 Å in thickness. The across area in each part was calculated and the method for calculating A_i for part i is the same as that for the monolayer graphene nanopore described in our previous work.³⁶ The normalized current is in direct proportion to 1/R_total under the same voltage, where R_total is the total resistance, with . Since R_i is directly proportional to 1/A_i², we have

I = V/R (3)

Fig. 5 Translocation of poly(A-T)₄₅ in the three-layer graphene nanopore. The atoms of poly(A-T)₄₅ captured by the nanopore (with the distance to the pore center < 1.2 nm) are shown by the CPK model, the graphene nanopore is shown in yellow by the vdW model, and the ions captured by the nanopore (with the distance to the pore center < 1.2 nm) are shown in green by the vdW model: (A) lateral view; (B) top view. (C) The black and red solid lines are the normalized current from the theoretical model and the current from the simulation for the SimD2 system, respectively.

Under the same voltage

The current calculated from eqn (7) is not the current observed in the simulation. To compare these two currents, the current from the model was normalized by dividing the open nanopore current which was also calculated from the model. As shown in Fig. 5C, the changes of the normalized current accord with that of the current in the 3-layer system with DNA fragment. This reflects that the model is able to describe correctly the current change in the DNA translocation. Since the ratio of the blockade current to open nanopore current is considered as the signal for distinguishing nucleotides, the change of normalized current could be thought as the real signal current. Thus, our model implies that a nucleotide could be distinguished with different unoccupied nanopore volumes and the resolution of DNA sequencing could be improved by modifying the nanopore volumes.

The evolution of the average current corresponds to three intervals, i.e. intervals a, b, and c. The current was blocked when the DNA fragment entered partially into the nanopore (interval a). With the majority of the DNA atoms entering into the nanopore, more current was blocked (interval b). Once the whole DNA molecule passed through the nanopore, the current was recovered (interval c). As mentioned above, this stepwise process was also observed with the 5-layer graphene nanopore. The stepwise change of the current comes as the result of using MLG nanopores. Compared with a monolayer system, an MLG nanopore can display more details about the current change. Therefore, increasing the thickness of a nanopore may improve the resolution in DNA sequencing.

3.4. Dynamics of dA and dT

In view of the importance of the translocation time in DNA sequencing, the dynamics of poly(A-T)₄₅ was investigated. Here, the movement of the CoM (center of mass) of the first residue of poly(A-T)₄₅ in the z direction was calculated. As we can see in the animation trajectory, the first four or five residues of poly(A-T)₄₅ were unzipped before entering into the nanopore. Unzipping of the double stranded DNA fragment upon going through a nanopore was also observed by other researchers,^8,11,49–51 and the unzipping strand poly(dA)₄₅ or poly(dT)₄₅ means dA and dT strand of the poly(A-T)₄₅, in respectively. In Fig. 6A, the first residue of poly(dA)₄₅ is denoted as dA₁ and the first residue of poly(dT)₄₅ is denoted as dT₁, respectively. We can see that the time interval between dA₁ entering into and leaving the nanopore is almost the same as that for dT₁. The time for poly(dA)₄₅ and poly(dT)₄₅ translocation through a nanopore of the same number of layers was essentially the same. However, an interesting point is that our simulations showed that poly(dT)₄₅ entered into the nanopore earlier than poly(dA)₄₅, as reflected by the vertical green dashed line in Fig. 6. The time for the first residue of poly(dA)₄₅ and poly(dT)₄₅ passing through the identical nanopore was thus virtually the same although their sequences are different.

Fig. 6 Time evolution of the position of the center of mass of the first residue of poly(dA)₄₅ (black line) and the first residue of poly(dT)₄₅ (red line) in the z direction (A) 3 layers, (B) 5 layers, (C) 7 layers and (D) 9 layers. The two blue lines correspond to the upper and lower limits of the graphene sheets in the z direction, respectively. The green line indicates the time when dT has left the nanopore while dA has not entered into it.

Since the DNA translocation dynamics depends on the DNA–pore interaction, we carried out further a series of simulations to study the adsorption of different nucleotides on a monolayer graphene sheet to gain insight into the DNA–pore interaction. In the simulation, the final state could be seen as the absorption state of graphene with nucleotide, and they are apart in the primary state. The enthalpy of adsorption could be seen as the interaction energy in final state of the simulation to minus that of the primary state. Since the interaction energy in the primary state are all zero in all systems, the value of interaction energy in the final state could be seen as the enthalpy of adsorption. As shown in Fig. 7, the interactions of the graphene with poly(dT)₅ and poly(dA)₅ are ca. 500 and 800 kJ mol⁻¹, respectively, which means that the interaction of poly(dA)₅ with the graphene sheet is much stronger than of poly(dT)₅. The strong interaction of poly(dA)₅ with the graphene sheet leads to that the time of poly(dA)₅ sticking to the graphene nanopore becomes much longer than that of poly(dT)₅ and thus explains why poly(dA)₄₅ enters into the nanopore later than poly(dT)₄₅. Therefore, the translocation time can be different for nucleotides with distinctive nucleotide–pore interactions. The interactions of dC and dT with the graphene sheet are almost the same, leading to poor resolution of dC and dT in the DNA sequencing, which is consistent with the results of Qiu et al.⁵² The interaction between dG and the graphene sheet is the largest, in accordance with the result of Zhao's et al.⁵³ The interaction of nucleotides with a graphene nanopore can be of crucial importance in distinguishing the nucleotides, and the resolution of DNA detection could therefore be improved by modifying the graphene nanopore surface.

Fig. 7 Interaction energy of different nucleotides with the monolayer graphene.

4. Conclusion

In this work we carried out molecular dynamics simulations to investigate the DNA translocation process through multi-layer graphene (MLG) nanopores. In particular, we addressed the importance of the dynamics and current change in DNA translocation to thread MLG nanopores, which so far have not received a detailed analysis. We found that the open nanopore resistance is directly proportional to the nanopore length. The contribution of K⁺ ions to the current was almost the same as that of Cl⁻. The translocation time increases with the increase of the number of graphene layers under a high electric field and reaches a maximum at a few layers (7), but decreases thereafter. This behavior was associated with the potential well in the nanopore. Based on the analysis of the DNA translocation through MLG nanopores, a model was constructed to explore the relationship between the current and the unoccupied volume of the nanopores. It was demonstrated that the blockade current is closely related to the unoccupied volume of the nanopores. We found that the ionic current underwent a stepwise change with the DNA passing through an MLG nanopore. Our study showed that the stepwise current came as the result of the increase of the nanopore thickness, meaning that the resolution could be improved by increasing the thickness of the nanopore to a certain range. We also found that due to the difference in the interaction between the nucleotides and the graphene sheet, the translocation process of poly(dT)₄₅ was earlier than that of poly(dA)₄₅ under the same conditions. Our work indicates that the interaction of the nucleotides with the graphene nanopore is of crucial importance in improving the discrimination of the nucleotides and that the resolution of DNA sequencing could be improved by modifying the nanopore surface. It could be helpful to applied graphene as a promising biosensor material for DNA sequencing.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (Grant no. 21273200 and 21074115), MOE (J20091551), Zhejiang Provincial Natural Science Foundation of China (no. LQ12F05001) and Zhejiang University (2011XZZX002, 2011QNA3014). The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the parallel computer centre (PDC), through the project “Multiphysics Modeling of Molecular Materials”, SNIC 020/11-23.

References

1. S. K. Min, W. Y. Kim, Y. Cho and K. S. Kim, Nat. Nanotechnol., 2011, 6, 162–165.
2. H. W. C. Postma, Nano Lett., 2010, 10, 420–425.
3. K. Healy, B. Schiedt and A. P. Morrison, Nanomedicine, 2007, 2, 875–897.
4. C. Dekker, Nat. Nanotechnol., 2007, 2, 209–215.
5. H. Yan and B. Q. Xu, Small, 2006, 2, 310–312.
6. D. M. Vlassarev and J. A. Golovchenko, Biophys. J., 2012, 103, 352–356.
7. Q. Liu, H. Wu, L. Wu, X. Xie, J. Kong, X. Ye and L. Liu, PLoS One, 2012, 7, e46014.
8. B. McNally, M. Wanunu and A. Meller, Biophys. J., 2007, 652a.
9. T. Z. Butler, J. H. Gundlach and M. A. Troll, Biophys. J., 2006, 90, 190–199.
10. R. F. Purnell and J. J. Schmidt, ACS Nano, 2009, 3, 2533–2538.
11. L. Franceschini, E. Mikhailova, H. Bayley and G. Maglia, Chem. Commun., 2012, 48, 1520–1522.
12. E. A. Manrao, I. M. Derrington, A. H. Laszlo, K. W. Langford, M. K. Hopper, N. Gillgren, M. Pavlenok, M. Niederweis and J. H. Gundlach, Nat. Biotechnol., 2012, 30, 349–353.
13. M. Wanunu and A. Meller, Nano Lett., 2007, 7, 1580–1585.
14. A. J. Storm, J. H. Chen, X. S. Ling, H. W. Zandbergen and C. Dekker, Nat. Mater., 2003, 2, 537–540.
15. M. J. Kim, M. Wanunu, D. C. Bell and A. Meller, Adv. Mater., 2006, 18, 3149–3153.
16. A. J. Storm, C. Storm, J. Chen, H. Zandbergen, J. F. Joanny and C. Dekker, Nano Lett., 2005, 5, 1193–1197.
17. A. Aksimentiev, J. B. Heng, G. Timp and K. Schulten, Biophys. J., 2004, 87, 2086–2097.
18. B. M. Venkatesan, J. Polans, J. Comer, S. Sridhar, D. Wendell, A. Aksimentiev and R. Bashir, Biomed. Microdevices, 2011, 13, 671–682.
19. H. Bayley, Nature, 2010, 467, 164–165.
20. S. Garaj, W. Hubbard, A. Reina, J. Kong, D. Branton and J. A. Golovchenko, Nature, 2010, 467, 190–193.
21. C. A. Merchant, K. Healy, M. Wanunu, V. Ray, N. Peterman, J. Bartel, M. D. Fischbein, K. Venta, Z. T. Luo, A. T. C. Johnson and M. Drndic, Nano Lett., 2010, 10, 2915–2921.
22. S. Liu, Q. Zhao, J. Xu, K. Yan, H. Peng, F. Yang, L. You and D. Yu, Nanotechnology, 2012, 23, 085301.
23. C. A. Merchant and M. Drndic, Methods Mol. Biol., 2012, 870, 211–226.
24. B. M. Venkatesan, D. Estrada, S. Banerjee, X. Jin, V. E. Dorgan, M. H. Bae, N. R. Aluru, E. Pop and R. Bashir, ACS Nano, 2012, 6, 441–450.
25. G. F. Schneider, S. W. Kowalczyk, V. E. Calado, G. Pandraud, H. W. Zandbergen, L. M. K. Vandersypen and C. Dekker, Nano Lett., 2010, 10, 3163–3167.
26. C. Sathe, X. Q. Zou, J. P. Leburton and K. Schulten, ACS Nano, 2011, 5, 8842–8851.
27. D. B. Wells, M. Belkin, J. Comer and A. Aksimentiev, Nano Lett., 2012, 12, 4117–4123.
28. D. Fologea, J. Uplinger, B. Thomas, D. S. McNabb and J. L. Li, Nano Lett., 2005, 5, 1734–1737.
29. K. J. Freedman, C. W. Ahn and M. J. Kim, ACS Nano, 2013, 7, 5008–5016.
30. G. Jo, M. Choe, C. Y. Cho, J. H. Kim, W. Park, S. Lee, W. K. Hong, T. W. Kim, S. J. Park, B. H. Hong, Y. H. Kahng and T. Lee, Nanotechnology, 2010, 21, 175201.
31. A. Kumar, K.-B. Park, H.-M. Kim and K.-B. Kim, Nanotechnology, 2013, 24, 495503.
32. W. Lv, M. Chen and R. a. Wu, Soft Matter, 2013, 9, 960–966.
33. B. Q. Luan, H. B. Peng, S. Polonsky, S. Rossnagel, G. Stolovitzky and G. Martyna, Phys. Rev. Lett., 2010, 104, 238103.
34. B. Q. Luan, G. Martyna and G. Stolovitzky, Biophys. J., 2011, 101, 2214–2222.
35. D. Y. Lu, A. Aksimentiev, A. Y. Shih, E. Cruz-Chu, P. L. Freddolino, A. Arkhipov and K. Schulten, Phys. Biol., 2006, 3, S40–S53.
36. L. Liang, P. Cui, Q. Wang, T. Wu, H. Agren and Y. Tu, RSC Adv., 2013, 3, 2445–2453.
37. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
38. D. Fologea, M. Gershow, B. Ledden, D. S. McNabb, J. A. Golovchenko and J. L. Li, Nano Lett., 2005, 5, 1905–1909.
39. H. Berk, C. Kutzner, D. V. D. Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
40. A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616.
41. L. J. Liang, Q. Wang, T. Wu, J. W. Shen and Y. Kang, Chin. J. Chem. Phys., 2009, 22, 627–634.
42. L. J. Liang, P. Cui, Q. Wang, T. Wu, H. Ågren and Y. Tu, RSC Adv., 2013, 3, 2445–2453.
43. B. M. Venkatesan and R. Bashir, Nat. Nanotechnol., 2011, 6, 615–624.
44. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
45. B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 075404.
46. Y. Kang, Y. C. Liu, Q. Wang, J. W. Shen, T. Wu and W. J. Guan, Biomaterials, 2009, 30, 2807–2815.
47. Q. Chen, Q. Wang, Y.-C. Liu, T. Wu, Y. Kang, J. D. Moore and K. E. Gubbins, J. Chem. Phys., 2009, 131, 015101.
48. W. P. Lv, S. J. Liu, X. Li and R. Wu, Electrophoresis, 2014, 35(8), 1144–1151.
49. A. Ferrantini and E. Carlon, J. Stat. Mech.: Theory Exp., 2011, 2011, P02020.
50. B. McNally, M. Wanunu and A. Meller, Nano Lett., 2008, 8, 3418–3422.
51. A. F. Sauer-Budge, J. A. Nyamwanda, D. K. Lubensky and D. Branton, Phys. Rev. Lett., 2003, 90, 238101.
52. H. Qiu and W. Guo, Appl. Phys. Lett., 2012, 100, 083106.
53. C.-L. Cheng and G.-J. Zhao, Nanoscale, 2012, 4, 2301–2305.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra05909c

---