Simulation of an axial–radial ammonia synthesis reactor by linking COMSOL–MATLAB software

Abstract

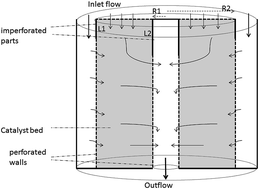
In this work a two dimensional mathematical model is developed for simulation of axial–radial ammonia synthesis reactors. Mass and energy balance equations are solved by a finite volume method using MATLAB (2012b) software. Momentum and general continuity equations, considering the effect of solid particles, are handled by COMSOL Multiphysics (4.3a). COMSOL is a Finite Element Method (FEM) software package for solving partial differential equations. By linking COMSOL and MATLAB software, momentum, mass, and energy balance equations are solved simultaneously. The MATLAB–COMSOL-LiveLink combines the powerful FEM abilities of COMSOL with the versatile programming environment of MATLAB. The effectiveness factor is calculated by the boundary value differential equation to consider the diffusion effect in catalyst particles. Furthermore the effect of pressure on ammonia concentration in the reactor is studied. Finally, simulation results are validated by the practical data of the Shiraz petrochemical plant.

---

1. Introduction

The increasing usage of ammonia in industry requires development of more efficient and cost effective synthesis reactors. Synthesis of ammonia from nitrogen and hydrogen is one of the most important processes in the petrochemical industry. Ammonia is an essential ingredient for a variety of fertilizers such as solid urea, ammonium nitrate, ammonium phosphates, and ammonium sulfate. Moreover, ammonia is used to manufacture fibers, plastics, explosives, and chemicals.¹ Ammonia synthesis reactor is the heart of an ammonia production plant. Numerous researches on the mathematical modeling of ammonia synthesis reactors have been done.^2–6 Many of these studies have shown that mathematical modeling is a convenient way to analyze and optimization of the reactor.^6–11

Recently, more advanced axial–radial reactors have been proposed that tries to utilize the advantages of both radial and axial reactors. The main advantages of the axial–radial reactors compared to the classical axial and radial reactors are lower pressure drop and higher catalyst utilization.¹² An axial–radial reactor contains one or more axial–radial beds. Each bed has two concentric cylindrical walls with a closed bottom. The catalyst is placed between the walls and the top part of each wall is closed to gas flow while the rest is perforated. Most part of the gas enters the catalyst bed radially and the remaining gas flows down in axial direction. Fig. 1 shows the overall layout of an axial–radial bed and the gas flow directions.

Fig. 1 Schematic illustration of an axial–radial bed.

Previous studies on the modeling and simulation of the axial radial reactors were focused on numerical methods and algorithms for solving momentum and continuity equations, and there is no clear simulation results (the results are just presented at the beds outlet and there is no concentration or velocity profiles in the beds),^12,13 furthermore in these studies orthogonal collocation method is used to solve the governing equations. The finite difference and orthogonal collocation methods convert the problem to a set of algebraic equations. When the equations is nonlinear, the resulting set of equations is also nonlinear. The solution of the nonlinear equations may not be unique and the generation of any solution may be difficult, moreover, accuracy of this method is strongly depends on the number of collocation points. In this work for accurate simulation of ammonia synthesis reactors COMSOL–MATLAB program linking is used.

2. Mathematical model

In this study the following assumptions are considered to develop the reactor model.

• The two dimensional heterogeneous model is considered.

• Heat and mass dispersions are negligible.⁷

• Steady-state operation is considered.

• The heat transfer resistance between the pellets and gas is negligible.⁷

• Due to symmetry in the θ direction of a cylindrical coordinate, the governing equations are independent of this direction.

2.1. Mass balance

Ammonia is considered as the reference component. The mass balance equation for a differential element in the catalyst bed gives:

The modified Temkin equation is used to calculate intrinsic rate of reaction, R_NH3, as follows:¹⁴

where α is a constant between 0.5 to 0.75.¹⁴ k₂ is estimated by an Arrhenius equation as follows:⁶

k₂ = 1.7698 × 10¹⁵ e^{−(40 765/R_gT)} (3)

The equilibrium constant, K_a, is calculated as:⁷

The components activity is defined as:

where, f⁰_i is reference fugacity and assumed to be atmospheric. Hence:

a_i = f_i = y_iϕ_iP (6)

The fugacity coefficients of nitrogen, hydrogen, and ammonia are determined from.¹⁴

2.2. Energy balance

Using the energy balance for a differential element in catalyst bed yields:

Here, the heat of reaction is calculated from the following equation:¹⁵

ΔH_r = 9723.24[−23 840.57 + (P − 300.0)(1.08 + (P − 300.0)(0.01305 + (P − 300.0)(0.83502 × 10⁻⁵ + (P − 300.00) × (0.65934 × 10⁻⁷)))) + 4.5(1391.0 − T)] (8)

C_f is specific heat for the gas mixture. Specific heat for pure components is a function of temperature and pressure that is given in.¹⁴

2.3. Effectiveness factor

The effect of diffusion through the catalyst pores is expressed by effectiveness factor term. This effect is considered by a molar differential balance for component i inside the catalyst particle:

In eqn (9) γ_i is stoichiometric coefficient of the i^th component. After some straightforward manipulations, eqn (9) can be rewritten as the following dimensionless form:⁷

The boundary conditions of this differential equation are as follows:

where ω = r/R_p, and C is the total concentration that is defined as:

Stefan–Maxwell equation for multicomponent diffusion is used for computing the diffusion coefficients of components as described in.¹⁶

After calculation of the intraparticle concentration from eqn (10), effectiveness factor can be estimated as:¹⁷

2.4. Continuity and momentum equations

The COMSOL Multiphysics software is used for solving continuity and momentum equations. COMSOL Multiphysics is a FEM software package for solving partial differential equations. defined momentum and continuity equations in the software is the Navier–Stokes–Brinkman equation as follows:¹⁸

∇·(ρu) = 0 (14)

where k_br is Brinkman permeability that is determined as:

Fig. 2 shows the overall two dimensional geometry of axial–radial bed. The boundary conditions used for the simulation are given in Table 1.

Fig. 2 Axial–radial bed geometry (boundaries described in Table 1).

Table 1 Boundary conditions used in axial–radial bed geometry

Boundary No.	Boundary Condition	Description
1,3,6	Wall	uz = 0; ur = 0
2	Inlet	ur = 0; P = Pin
4	Inlet	uz = 0; P = Pin
5	Outlet	uz = 0; mass flow rate = m°

---

3. Numerical solution algorithm

A two dimensional mathematical model was developed for the axial–radial reactor simulation. The governing equations is consisting of mass, energy and momentum balances that are solved iteratively. In the case of two dimensional modeling, partial differential equations are involved and an analytical solution is usually impossible. One has to use advanced numerical technics and computing aids to solve such models. As mentioned in Section 1, in the previous studies orthogonal collocation method is used to solve the governing equations. Although the accuracy of the collocation method can be improved as much as it is desired by increasing the number of collocation points, it will increase the computational time. In this study, COMSOL Multiphysics software that is based on FEM is used to solve the momentum and continuity equations. By the initial guess of the density and viscosity profiles (first guess can be the density and viscosity at inlet conditions) the velocity profiles obtained using COMSOL software. By using LIVELINK for MATLAB, the COMSOL results can be accessed by MATLAB (Appendix A). Using velocity profile, mass and energy balances are solved by finite volume method in MATLAB software. From its solution, the new density and viscosity profiles are calculated. The procedure stops when the maximum change in the concentration and temperature between two iterations reaches to 0.001% and 5% respectively.

4. Simulation results and discussion

The operating conditions and the data used in the simulation are given in Table 2.

Table 2 Operating conditions and data used in the simulation of an axial–radial ammonia synthesis reactor

Bed characteristics
	R1 (m)	R2 (m)	L1 (m)	L2 (m)	L (m)
Bed 1	0.328	1.169	0.40	0.60	2.91
Bed 2	0.454	1.155	0.46	0.65	4.53
Bed 3	0.504	1.154	0.61	0.80	6.92

---

Operating conditions
Feed flow rate (kmol h^−1):	19622.17
Operating pressure (atm):	220
Inlet temperature (K):	615
Feed compositions:
y0_NH3	0.0347
y0_N2	0.2093
y0_H2	0.6280
y0_Ar	0.0341
y0_CH4	0.0939

---

The results are given in Fig. 3 and 4. Fig. 3a and b show the streamlines and pressure profile respectively. Fig. 3c shows the radial velocity component in the first bed.

Fig. 3 (a) streamlines, (b) pressure profile (P (atm)), (c) radial component of velocity profile (u_r (m s⁻¹)), in the first bed.

Fig. 4 Ammonia concentration profile in first bed at P_in = 220 atm.

As shown in Fig. 3 most of the feed gas inters the catalyst bed through the perforated wall in radial direction. And the remaining gas flows down through the catalyst bed in an axial direction.

Fig. 4 shows the ammonia concentration profile in the first bed. The velocity in the axial direction is relatively low and at the top of the bed there is no radial flow, hence the concentration will increase sharply in this part of the bed.

In following the simulation is carried out at P_in = 250 and 300 atm to study the effect of pressure on outlet ammonia concentration. Fig. 5 shows the ammonia concentration profile at P_in = 250 atm.

Fig. 5 Ammonia concentration profile in first bed at P_in = 250 atm.

As expected ammonia concentration is increased by increasing the pressure because higher pressure is thermodynamically favorable for ammonia synthesis reaction. Moreover, density and viscosity increase due to pressure rise hinders the velocity increase.

The simulation results are summarized in Tables 3 and 4. Table 3 shows the simulation result at the first bed outlet and the effect of pressure on outlet concentrations. As mentioned, higher pressure is thermodynamically favorable for ammonia synthesis and increase of the ammonia conversion was expected. Table 4 shows the simulation results at the second and third bed outlet. As it can be seen in Tables 3 and 4, nitrogen conversion (and consequently ammonia mole fraction) in the first bed is higher than those of the second and third ones. This is mainly for lower ammonia content in the first bed. Note that the given concentrations and temperatures are average values at the beds outlet.

Table 3 First bed simulation results at P_in = 220, 250, and 300 atm

Bed:	I
	Inlet (mol%)	Outlet
		Cal. (300 atm)	Cal. (250 atm)	Cal. (220 atm)	Exp. (220 atm)
NH3	3.47	15.46	14.67	13.05	14.05
N2	20.93	17.51	17.78	18.25	17.96
H2	62.80	52.63	53.36	54.74	53.9
CH4	9.39	10.58	10.41	10.25	10.33
Ar	3.41	3.82	3.78	3.71	3.76
Temp (°C)	342	539.7	521.2	494.2	494.7

---

Table 4 Second and third beds simulation results at P_in = 220 atm

Bed:	II				III
Compon.	Inlet (mol%)	Outlet		Relative error (%)	Inlet (mol%)	Outlet		Relative error (%)
		Cal.	Exp.			Cal.	Exp.
NH3	11.13	16.17	16.63	2.75	16.17	20.19	20.24	0.25
N2	18.78	17.37	17.23	0.81	17.37	16.23	16.22	0.62
H2	56.34	52.10	51.71	0.75	52.10	48.70	48.67	0.61
CH4	10.09	10.55	10.58	0.28	10.55	10.92	10.91	0.91
Ar	3.66	3.83	3.84	0.26	3.83	3.96	3.96	0
Temp (°C)	407.0	484.08	480.4	0.85	400.0	448.5	445.2	0.75

---

Results in Tables 3 and 4 demonstrate a good agreement between the simulated and industrial data.

5. Conclusions

In this study, a two dimensional mathematical model for ammonia synthesis reactor is solved by MATLAB and COMSOL softwares. By using FEM instead of Orthogonal Collocation method for solving the momentum and continuity equations, the simulation results show significant improvement compared to previous studies. This implies that using Finite Element Method (FEM) is more accurate than the orthogonal collocation method for solving momentum equations. The maximum relative error between measured and calculated temperatures was 0.85% that shows a great improvement compared to 2% error of conventional scheme. Therefore using COMSOL and MATLAB software link can be an accurate tool for simulation of fixed bed reactors.

Appendix

By using the LiveLink interface the MATLAB programing tools can be combined with the COMSOL model object. One benefit of this integration is to access results at the MATLAB workspace. Furthermore, it enables integration of COMSOL modeling commands into MATLAB scripts. Hence, one can take full advantage of all available tools for controlling the flow of the code. This section explains how to do this effectively by introducing MATLAB variables into COMSOL model and updating only the affected parts of the model object.¹⁹

COMSOL has an option to save the model as an M-file which is updated during the modeling. Then we have to modify the saved M-File by adding the input variables of the axial–radial model to the MATLAB function.

Next step is to start the COMSOL–MATLAB LiveLink (Windows: COMSOL with MATLAB, Linux: COMSOL server MATLAB, alternatively using mphstart.m in the COMSOL installation directory). Finally, load the axial–radial example model from the Model Library using mphload command as:

>model = mphload (‘axial–radial’);

The mphload command automatically searches the COMSOL path to find the requested file. Mpheval function evaluates the velocity and pressure, which are the axial–radial model dependent variables. Mpheval uses the nodes of a simplex mesh to evaluate the function. To get data at a specific location not necessarily defined by node points, mphinterp command can be used to interpolate the results. The interpolation method uses the shape function of the elements.¹⁹

Nomenclature

aH2, aNH3, aN2	Activity of hydrogen, ammonia and nitrogen
A	Crosse section area of beds (m^2)
C	Total concentration (kmol m^−3)
cNH3	Concentration of NH3 (kmol kg^−1)
Cpmix	Specific heat of gas mixture (kJ kg^−1 K^−1)
Die	Effective diffusion coefficient of component i (m^2 h^−1)
fi	Fugacity of component i (kPa)
f^0i	Reference fugacity of component i (kPa)
	Initial molar flow rate of nitrogen (kmol h^−1)
Ka	Equilibrium constant of reaction
k2	Reverse reaction rate constant
L	Bed length (m)
m°	Mass flow rate (kg h^−1)
Mav	Average molecular weight (kmol kg^−1)
Ni	Molar flux of component i at catalyst particle (kmol m^−2 h^−1)
P	Pressure (kPa)
R	Radial coordinate of catalyst particle (m)
Rg	Universal gas constant (kJ kmol^−1 K^−1)
Rp	Equivalent radius of the catalyst particle (m)
RNH3	Intrinsic rate of reaction (kmol m^−3 h^−1)
T	Temperature (K)
u	Velocity vector (m h^−1)
ur	Radial component of velocity (m h^−1)
uz	Axial component of velocity (m h^−1)
yi	Mole fraction of component i
y^si	Mole fraction of component i in catalyst particle

Greek symbols

ε	Porosity of catalyst bed
η	Effectiveness factor
ϕi	Fugacity coefficient of component i
ΔHr	Heat of reaction (kJ kmol^−1)
μ	fluid viscosity (Pa s)
ρ	Density (kg m^−3)

References

1. M. Appl, Ammonia: Principles and Industrial Practice, WILEY-VCH, 1999.
2. B. Babu and R. Angira, Comput. Chem. Eng., 2005, 29, 1041–1045.
3. J. N. Sahu, S. Hussain and B. C. Meikap, Korean J. Chem. Eng., 2011, 28, 1380–1385.
4. M. Abashar, Math. Comput. Model., 2003, 37, 439–456.
5. C. Pan, Y. Li, W. Jiang and H. Liu, Chin. J. Chem. Eng., 2011, 19, 273–277.
6. C. P. P. Singh and D. N. Saraf, Ind. Eng. Chem. Process Des. Dev., 1979, 18, 364–370.
7. S. S. Elnashaie, M. Abashar, E. A.-U. Mohamed and S. Abdulrahman, Ind. Eng. Chem. Res., 1988, 27, 2015–2022.
8. S. Siddiq, S. Khushnood, Z. U. Koreshi and M. T. Shah, Technical Journal, 2011, 84–109.
9. R. Angira, Int. J. Chem. React. Eng., 2011, 9, 1.
10. M. T. Sadeghi and A. Kavianiboroujeni, Int. J. Chem. React. Eng., 2008, 6, A113.
11. M. J. Azarhoosh, F. Farivar and H. A. Ebrahim, RSC Adv., 2014, 4, 13419.
12. F. Zardi and D. Bonvin, Chem. Eng. Sci., 1992, 47, 2523–2528.
13. M. Panahandeh, J. Fathikaljahi and M. Taheri, Chem. Eng. Technol., 2003, 26, 666–671.
14. D. C. Dyson and J. M. Simon, Ind. Eng. Chem. Fundam., 1968, 7, 605–610.
15. L. D. Gaines, Ind. Eng. Chem. Process Des. Dev., 1977, 16, 381–389.
16. S. Elnashaie and S. Elshishini, Modelling, Simulation and Optimization of Industrial Catalytic Fixed Bed Reactors, Gordon and Breach Science, Netherlands, 1993.
17. R. G. Rice and D. D. Do, Applied mathematics and modeling for chemical engineers, Wiley, 2nd edn, 2012.
18. L. Guta and S. Sundar, Tamkang Journal of Mathematics, 2010, 41, 217–243.
19. COMSOL, Inc, Introduction to LiveLink™ for MATLAB, 2012.

---