Intramolecular OHO bonding in dibenzoylmethane: symmetry and spectral manifestations

Abstract

Although both experimentalists and theoreticians agree that dibenzoylmethane exists in the enol form, there are different opinions concerning symmetry of the OHO fragment. Consequently, assignment of its vibrational spectra has been incomplete. In this contribution we computed Gibbs free energies with the G4MP2 method. Multi-dimensional potential energy surfaces obtained at M06-2X/cc-pVTZ level enabled vibrational analysis and comparison with available experimental data. Our results revealed presence of two conformers in the gas phase at room temperature, the asymmetric structure (with O–H stretching frequency around 2400 cm⁻¹ and very low infrared intensity), and the symmetric conformer (with O⋯H⋯O asymmetric stretching band located around 500 cm⁻¹). Characterization of hydrogen bonds was performed with quantum theory of atoms in molecules (QTAIM), which showed that O–H⋯O group represents a typical hydrogen bond, whereas hydrogen bonds in the O⋯H⋯O fragment have substantial covalent character.

---

1 Introduction

Dibenzoylmethane (DBM) derivatives are important as organic reagents, but are also used in pharmaceutical industry due to their photostability.¹ Recent investigations suggest the possibility to use them as chemopreventive agents² and in production of organic light-emitting diodes.³ There is a long-lasting controversy concerning geometry of DBM and its vibrational properties. Dibenzoylmethane is a β-dicarbonyl compound liable to keto-enol tautomerization, since formation of an intramolecular hydrogen bond significantly stabilizes the enol form. Evidences that DBM is present as enol tautomer were provided by spectroscopic measurements (IR, UV and NMR)^4–10 and theoretical analysis.^8,11,12 Hence, in the present contribution we will focus on the enol structure.

Seemingly conflicting assignments were made with regard to symmetry of the OHO fragment. Some studies suggest an asymmetric structure^10,12–15 with the hydrogen atom closer to one of the oxygen atoms, while others predict an almost symmetric structure where hydrogen atom is delocalized between the oxygen atoms.^16–19 The two structures are shown in Fig. 1. Borisov et al. performed an NMR study and found that in the temperature range from 181 to 268 K hydrogen bond is asymmetric.¹⁰ Their results imply that lowering the temperature modestly increases hydrogen bond strength. Also, according to gas-phase electron diffraction and a single molecule DFT studies performed by Tayyari et al. hydrogen bond in DBM is asymmetric.¹⁵ On the other hand, Gilli and coworkers used variable temperature X-ray techniques to analyze a series of β-dicarbonyl compounds¹⁸ and concluded that DBM represents a single well system. More recent experiments by Thomas et al.¹⁹ indicate that increase in temperature influences the position of the bridging hydrogen, shifting it closer to the midpoint between the two electronegative atoms.

Fig. 1 The asymmetric and the symmetric structure of dibenzoylmethane. The structural parameters are obtained at M06-2X/cc-pVTZ (SCS-CC2/cc-pVTZ) level.

In this contribution we attempt to shed light on the structure and vibrational properties of gas phase DBM based on theoretical investigations.

2 Computational details

Geometry optimization and subsequent harmonic frequency calculations were performed with the Gaussian program package²⁰ (density functional theory – B3LYP^21,22 and M06-2X²³ functionals, together with cc-pVDZ²⁴ and cc-pVTZ²⁵ basis sets, and with second-order Møller-Plesset theory (MP2)^26,27 in conjunction with cc-pVDZ basis set) and with the Turbomole package²⁸ (at SCS-CC2/cc-pVTZ and CC2/cc-pVTZ levels of theory^29–33). Gaussian suite of programs was also used for high accuracy energy calculations (G4MP2 (ref. 34) approach), as well as natural bond orbital (NBO) analysis (version 3.1)^35,36 of the M06-2X/cc-pVTZ optimized structures. Identification of bond critical points and analysis of properties of electron density were performed with the Multiwfn³⁷ program.

All quantum chemistry calculations beyond harmonic approximation were performed with M06-2X functional. The focus of our research are fragments with hydrogen bonds, O–H stretch of the asymmetric conformer, and asymmetric O⋯H⋯O stretch of the symmetric species. In order to identify vibrational degrees of freedom that influence the dynamics of the two modes of interest, we computed corresponding anharmonic force constants. Further, it was necessary to establish the impact each of thus selected modes has on the frequencies of O–H/O⋯H⋯O stretch by computing two-dimensional potential energy surfaces, with one coordinate being O–H/O⋯H⋯O stretch. Those 2D models enabled determination of the frequency of the O–H stretching mode. Most strongly coupled modes of the symmetric species are used for construction of two 3D models. The IR spectra computed with those 3D Hamiltonians were used to establish the position of the peak in the IR spectrum that corresponds to the O⋯H⋯O asymmetric stretching motion. Multi-dimensional wavefunctions were propagated and analyzed with the MCTDH program package.³⁸

3 Results and discussion

Due to the fact that there are experimental results that favor both the symmetric and the asymmetric structure of dibenzoylmethane, we have analyzed both species. In all cases, the asymmetric structure (A) corresponds to a minimum on the potential energy surface, whereas the symmetric structure (S) represents a transition state for hydrogen transfer. These results seem to be sufficient to focus further analysis on the A conformer only. Nevertheless, previous investigations of certain hydrogen bonded species have shown that only stable conformers (according to the position on the potential energy landscape) cannot always provide full understanding of their properties (for example vibrational spectra³⁹ or proton transfer reactions⁴⁰). Thus, we took a closer look at energies that take into account vibrational and thermal motion. Energy differences given with respect to the A structure are compiled in Table 1. Electronic energy of the A conformer is lower than the one of the S conformer, whereas inclusion of the zero point energy gives a reversed situation. Also, the S species is more stable according to the Gibbs free energy. It is important to keep in mind that the symmetric form possesses one imaginary frequency, which was not considered when zero point energy and the Gibbs free energy were computed. Thus, the results presented in Table 1 should be taken with caution – they are shown only in order to justify further analysis of both conformers.

Table 1 Differences in electronic energies (with and without ZPE) and Gibbs free energies between the symmetric and the asymmetric structure in kJ mol⁻¹. The results correspond to the pressure of 1 atm and temperature of 298.15 K

QC level	ΔE^el	ΔE^elZPE	ΔG
B3LYP/cc-pVDZ	5.08	−4.30	−2.87
M06-2X/cc-pVDZ	5.35	−3.85	−3.60
MP2/cc-pVDZ	8.45	−1.59	−0.70
B3LYP/cc-pVTZ	7.37	−2.69	−2.84
M06-2X/cc-pVTZ	7.66	−2.25	−1.57
SCS-CC2/cc-pVTZ	8.27	−1.43	−7.57
CC2/cc-pVTZ	3.16	−5.44	−7.69

---

Due to the spread of results presented in Table 1, we used a more advanced method to precisely determine the energies of the two species. The difference in Gibbs free energies obtained with the G4MP2 method (at 298.15 K and 1 atm) amounts to 2.89 kJ mol⁻¹. Thus, it predicts the A species to be more stable. The computed energy difference is comparable with thermal energy at 298.15 K that is equal to 2.48 kJ mol⁻¹, and since the equilibrium constant for A ↔ S transformation equals 0.311 (as predicted with the G4MP2 method), at room temperature both species are present. Those results differ from the values presented in Table 1, all of which predict the Gibbs free energy of the symmetric species to be lower. Particularly, G4MP2 value is significantly different from SCS-CC2/cc-pVTZ and CC2/cc-pVTZ results. The reason for this discrepancy is twofold: (1) more precise computation of electronic energies with the G4MP2 approach, and (2) approximate inclusion of anharmonic effects, since the harmonic frequencies (needed for the computation of ZPE and entropy) are scaled within G4MP2 method. Thus, inclusion of anharmonicity stabilizes conformer A to a greater extent than S. The fact that SCS-CC2 and CC2 methods predict larger deviation from G4MP2 results for ΔG compared to B3LYP, M06-2X and MP2 is most likely due to favorable cancelation of errors in the latter case.

3.1 Structural properties

Bond lengths of A and S structures obtained at M06-2X/cc-pVTZ and SCS-CC2/cc-pVTZ levels are presented in Fig. 1. Structural parameters obtained at other optimization levels are given in ESI, Tables S1 and S2.† As a general trend, the M06-2X optimized bond distances are somewhat shorter than the corresponding SCS-CC2 values. However, the SCS-CC2 bond lengths depend on the basis set and increase of the basis set is expected to contract the SCS-CC2 bond lengths. The A geometry is nonplanar with a butterfly shape. The largest bond differences are encountered for C₂–O₁, C₃–O₂, C₁–C₂ bonds, 0.014, 0.021, 0.011 Å respectively. The S structure is nonplanar as well. Interestingly, for this structure, the M06-2X and SCS-CC2 methods give very similar bond lengths. As for the A structure, the largest difference is encountered for C–O bonds, namely 0.007 Å. Comparing with the A structure, the S structure has not only hydrogen atom in the midway between the oxygen atoms, but also the character of the C₂–O₁, C₂–C₁, C₁–C₃ and C₃–O₄ bonds changes. The C₂–O₂ and C₁–C₃ bonds shrink while the C₂–C₁ and C₃–O₄ bonds elongate.

Electron diffraction studies performed on the gas phase are reported in ref. 12. These results are in good agreement with our results for the A structure, but it should be emphasized that they were obtained by fixing certain parameters to calculated B3LYP/cc-pVTZ values of the optimized asymmetric structure. X-ray and neutron diffraction studies of this system exist but it should be kept in mind that such studies were performed with the crystalline state that contains intermolecular hydrogen bonds and stacking effects.^{13,14,16–19} Although there are no gross differences between all crystal structures, there are some discrepancies between them concerning the position of the hydrogen atom in the intramolecular hydrogen bond. These discrepancies are caused by the way bond lengths are corrected for thermal motion of atoms.¹⁴ As stressed in ref. 19, X-ray and neutron diffraction experiments test different properties: the former gives information on the electron density, and the later on nuclear position. They combined the two approaches and reached to a conclusion that at low temperatures the OHO moiety is slightly asymmetric, while increase of temperature leads to an almost symmetric structure. Comparing our calculated and experimental values, we find that our results for the S conformer are in reasonable agreement with the neutron diffraction data provided in ref. 17, which predict slightly asymmetric structure. On the other hand, the distance difference from the hydrogen atom to oxygen atoms in the A conformer in the harmonic approximation given in Table 2 is significantly higher than 0.2 Å that is predicted by X-ray experiments.¹⁴

Table 2 Distance difference between the hydrogen atom and the oxygen atoms in Å in the asymmetric structure, and harmonic ν_OH frequency and ν^a_OHO frequency in cm⁻¹

QC level	ΔrOH	νOH	ν^aOHO
B3LYP/cc-pVDZ	0.481	2665	949
M06-2X/cc-pVDZ	0.477	2728	1078
MP2/cc-pVDZ	0.552	2946	1092
B3LYP/cc-pVTZ	0.541	2846	1040
M06-2X/cc-pVTZ	0.549	2938	1113
SCS-CC2/cc-pVTZ	0.555	2895	1075
CC2/cc-pVTZ	0.439	2479	818

---

The results presented in Tables 1 and 2 show that computed energy differences and structural parameters are very sensitive on the level of theory. One would prefer always to use sophisticated approaches in order to obtain more reliable and more precise results. However, as will be shown later, analysis of hydrogen bonded systems requires treatment of mode couplings and computation of high-dimensional potential energy surfaces. For this reason, we have decided to turn to density functional theory which provides with reliable results at reasonable cost. Among many functionals, we decided to use B3LYP and M06-2X for analysis within harmonic approximation, both of which are known to give reliable description of non-covalent interactions.^23,41–45 M06-2X functional was chosen for a more detailed study of DBM due to the fact that recent investigations showed that it is slightly superior over B3LYP for describing hydrogen bonded systems.^46,47

3.2 Characterization of hydrogen bonds by QTAIM and NBO analysis

One of the hydrogen bond properties is its formation energy, E_HB. Generally, strong hydrogen bonds have energies higher than 60 kJ mol⁻¹ (cf. ref. 48 and references therein). A theoretical method suitable for estimation of hydrogen bond energy is Bader's quantum theory of atoms in molecules.⁴⁹ Although it does not directly provide relation between electron density and bond energy, several empirical relations were proposed.^50–52 In this work, we will use linear relation between electron density and formation energy given by Nikolaienko et al.⁵² for intramolecular OH⋯O hydrogen bonds: E_HB = −3.09 + 239 × ρ(r_c) (kcal mol⁻¹), where ρ(r_c) is electron density in atomic units at the bond critical point (BCP). Determination of BCP locations was performed with the Multiwfn program³⁷ for M06-2X/cc-pVTZ optimized structures. (3, −1) BCPs of A and S are shown on Fig. S1 in the ESI.† ρ(r_c) was found to be 0.0707 and 0.1784 for A and S structures, respectively, giving the hydrogen bond formation energies 57.78 and 165.48 kJ mol⁻¹. Although these numbers are of qualitative value, they show that in both structures the hydrogen bond is strong and that in S its strength can compare even with a covalent bond.⁵³

Beside electron density itself, other topological properties of electron density enable better understanding of hydrogen bonded systems.⁵⁴ Table 3 comprises certain properties of the two species in BCP. The total energy density H(r_c), which is the sum of kinetic energy density G(r_c) and potential energy density V(r_c)

H(r_c) = G(r_c) + V(r_c) (1)

is negative for both conformers at BCP, i.e. the absolute value of V(r_c) is larger than G(r_c). Further, the relation between G(r_c), V(r_c) and ∇²ρ(r_c) is given by⁴⁹

Table 3 Topological properties of electron densities for the A and S conformers obtained at BCPs of the M06-2X/cc-pVTZ optimized structures: electron density ρ(r_c), kinetic energy density G(r_c), potential energy density V(r_c), total energy density H(r_c), and Laplacian of electron density ∇²ρ(r_c). All values are given in atomic units

Property	A	S
ρ(rc)	0.07071	0.17840
G(rc)	0.05492	0.09470
V(rc)	−0.08303	−0.29680
H(rc)	−0.02811	−0.20210
∇^2ρ(rc)	0.10724	−0.42963

---

Since the Laplacian is positive for the A system (2G(r_c) > |V(r_c)|), ρ(r) has a minimum value in BCP and electron density increases upon approaching H and O atoms, the interaction is both closed-shell and shared-shell with dominant electrostatic interactions, i.e. the OH⋯O bond represents a typical hydrogen bond.^54,55 On the other hand, the negative value of ∇²ρ(r_c) for the S species (2G(r_c) < |V(r_c)|) means that ρ(r) has a maximum value in BCP. This represents another proof of substantial covalent character of O⋯H⋯O hydrogen bonds.^49,54,55

Let us now discuss the results from Natural bond orbital (NBO) analysis. The strongest delocalization in A results from π* of O₂=C₃ to σ* of C₁=C₂ and C₅=C₁₁ interactions (cf. Fig. 1): the corresponding energies for π*(O₂C₃) → σ*(C₁C₂) and π*(O₂C₃) → σ*(C₅C₁₁) amount to 167.63 and 162.69 kcal mol⁻¹, respectively. The strongest interaction that involves the hydrogen atom of interest is O₂(2) → σ*(O₁H) (the lone pair of the oxygen atom O₂ to the antibond of σ* of O₁H) which is computed to be 40.07 kcal mol⁻¹. In the S structure, the strongest charge transfer occurs from lone pairs of oxygen atoms to the antibond of the hydrogen atom, and each energy transfer is equal to 248.04 kcal mol⁻¹. Further, natural atomic charges of atoms O₁, H and O₂ in the A structure are −0.671, 0.519 and −0.650, respectively. The corresponding charges in the S structure are −0.660 for the oxygen atoms and 0.501 for the bridging hydrogen. Computed high positive hydrogen natural charges confirm strong hydrogen bonds for both structures.

3.3 O–H and O⋯H⋯O stretching motion

Although the first step in each quantum chemical analysis is geometry optimization, the optimized structures provide only limited information. The atoms are in constant motion, and in order to arrive at a realistic picture, it is necessary to drift from the stationary points and probe their neighbourhood on the potential energy landscape. We will focus on the points that can be reached upon stretching motion of the bridging hydrogen between oxygen atoms. For the A molecule, that is the O–H stretching vibration ν_OH, whereas in the S conformer it is asymmetric O⋯H⋯O stretching vibration ν^a_OHO. The harmonic O–H stretching frequencies calculated at various levels of theory are compiled in Table 2. The computed values range from 2479 to 2946 cm⁻¹. The obtained O⋯H⋯O stretching frequencies span the range between 818 and 1113 cm⁻¹in the harmonic approximation at different levels of theory. Despite which method and basis set are combined, the bridging hydrogen atom is more firmly bound to the electronegative atoms in the asymmetric system, i.e. the values of the ν_OH frequencies are significantly larger than the ν^a_OHO frequencies.

Harmonic approximation gives only a rough description of DBM: formation of a hydrogen bond introduces anharmonicity in the potential energy surface^{39,42,56–66} and governs system's properties. In order to prove this statement, we performed anharmonic frequency calculations through a perturbative treatment of all cubic, and diagonal and semi-diagonal quartic anharmonic terms as implemented in the Gaussian program package.^67–69 We used predefined values for normal mode displacements for numerical calculations of anharmonic force fields. Since the molecules possess 81 vibrational degrees of freedom, the M06-2X functional was used with a smaller basis set, cc-pVDZ. These results were supposed to provide a reliable qualitative picture for the influence of other vibrations on O–H and O⋯H⋯O stretching. The frequencies were shifted from the harmonic 2728 cm⁻¹ (A) and 1078 cm⁻¹ (S) to 1365 cm⁻¹ (50% red shift) and 1754 cm⁻¹ (60% blue shift). Although these results do not properly describe the phenomenon we are interested in (precise calculations require a more rigorous treatment between strongly coupled modes, beyond the three types of mentioned anharmonic terms), they are an indication that the anharmonicity is very strongly pronounced in both systems. Interestingly, inclusion of electric anharmonicity drastically decreases the intensity of the ν_OH band from harmonic 665, to anharmonic 3 km mol⁻¹. This means that the peak in the IR spectrum that corresponds to the O–H stretch is not visible. Nevertheless, we will estimate it's frequency in order to compare it with the ν^a_OHO frequency.

Further calculations beyond harmonic approximation were performed with the M06-2X functional in conjunction with the cc-pVTZ basis set. Starting from the two optimized structures, we constructed models with increasing complexity in order to arrive at a valid picture of DBM. First, let us establish the orientation of the structures: the origin of the coordinate system is placed in the midpoint between the two oxygen atoms, while the hydrogen atom with the two oxygen atoms defines the xy plane, Fig. 2. Atom C₁ points in the positive direction of the z-axis. Thus, O⋯H⋯O stretching motion takes place predominantly along the x-axis, whereas O–H stretching involves changes of x and y coordinates.

Fig. 2 Schematic representation of the orientations of the A and S structures.

3.3.1 1D normal mode and Cartesian representation. Decision on which representation one should use to describe a certain system is governed by its nature and properties that are to be described. Vibrational motion is often described by Cartesian, normal mode and internal coordinates. Although internal coordinates seem to be the natural choice in case certain vibration basically involves change of a bond length, or angle between the bonds, the drawback are complications that arise upon construction of models of higher dimensionality. Namely, in the picture constructed by internal coordinates, couplings between the degrees of freedom are contained in the kinetic energy operator, and the more complex the model (more degrees of freedom included), the more troublesome this part of the Hamiltonian becomes. On the other hand, couplings among the degrees of freedom in Cartesian and normal mode representation are contained in the potential energy part of the Hamiltonian, and all one needs to do is to compute a potential energy surface on a grid. Since DBM represents a hydrogen bonded system and thus couplings among vibrational degrees of freedom are expected to be pronounced, we decided to use Cartesian and normal mode coordinates. In DBM, proton donor and proton acceptor are connected to heavy fragments (–C–C₆H₅), which indicates that motion of the light hydrogen atom might be separated from the rest of the molecule. This justifies an attempt to build models established on Cartesian coordinates. The simplest model in Cartesian representation for analysis of O⋯H⋯O stretching vibration of the S structure would be one-dimensional (motion of the hydrogen atom along the x-axis), and for the O–H stretching vibration of the A conformer it would be two-dimensional (motion of the hydrogen atom in the xy plane). For start, we will analyze 1D potentials of both systems in both representations. 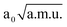All four potentials were computed on 45 grid points in the range −0.80 Å ≤ H^S_x ≤ 0.80 Å, −1.05 Å ≤ H^A_x ≤ 1.00 Å, −0.95 ≤ 0.95 and −1.90 ≤ Q_νOH ≤ 0.60 ( and Q_νOH are normal coordinates). The curves are displayed in Fig. 3. In Cartesian coordinates, the potential energy curve for S is a symmetric double well potential with the reference structure 41 cm⁻¹ above the minima. The curve for the A species predicts only an extremely shallow local minimum that corresponds to the formation of the covalent O₂–H bond. The curve is not symmetric due to the fact that the reference geometry corresponds to a structure with the covalent O₁–H bond. In the normal mode representation, there is a single minimum for A in the energy range up to 10 000 cm⁻¹, whereas the curve for the S conformer is a symmetric double-well potential with a barrier height of 201 cm⁻¹.

Fig. 3 1D potential energy curves computed in (A) Cartesian coordinates and (B) normal mode coordinates. The asymmetric/symmetric curves correspond to the A/S species.

Anharmonic frequencies within these 1D models were computed by diagonalizing the Hamiltonian with the Lanczos–Arnoldi integration scheme,^70–72 as implemented in the MCTDH program package.^38,73 The computed ν_OH frequency is 2620 cm⁻¹ and differs by almost 300 cm⁻¹ from the harmonic value. The resulting O⋯H⋯O strecthing frequencies are 1233 and 931 cm⁻¹ in Cartesian and normal mode representation, respectively. The discrepancy of approximately 300 cm⁻¹ between these two values indicates that this system cannot satisfactorily be represented with a simple model based on Cartesian coordinates. Namely, the experimental spectra reflect group vibrations,⁷⁴ i.e. each vibration involves motion of all atoms (the center of mass must not move upon vibrational motion), and there are a few modes that involve large displacements of the bridging hydrogen between the two oxygen atoms (that is, H-motion along the x-axis) due to mode mixing. Two such modes are displayed in Fig. 4. Those two modes represent C=O and C=C stretching motion, but to a great extent they also involve motion of the hydrogen atom between the electronegative atoms, and in order to arrive at a Cartesian model that would be able to explain the experimental IR spectrum, it would be necessary to include many degrees of freedom, which would require computation of a potential surface of very high dimensionality, that is far too expensive. Thus, for the analysis of vibrational properties of DBM it is more convenient to employ and improve the above mention 1D normal mode picture.

Fig. 4 Two normal mode vibrations of the symmetric conformer with predominantly C=O/C=C stretching motion (up/below). For better visibility, normal mode displacements are multiplied by factor 2.

3.3.2 2D models. In order to identify vibrational degrees of freedom that ν_OH and ν^a_OHO are coupled to, we computed the corresponding cubic and quartic anharmonic force fields according to the procedure described in ref. 75. To simplify the discussion, we will consider only the absolute values of the anharmonic terms. Cubic anharmonic force constants, and diagonal and semi-diagonal quartic force constants whose absolute values are larger than 25 cm⁻¹ are provided in ESI, Tables S3–S6.† The limit 25 cm⁻¹ was used due to the fact that coupling below this value is very weak, and the number of anharmonic force constants is large (3321 cubic, and 3321 diagonal and semi-diagonal quartic terms). The aim of our work was not to compute high resolution IR spectrum, but to estimate the position of the peak of interest. For this purpose, it is sufficient to include only the strongest couplings, so we used the threshold of 500 cm⁻¹ for the cubic terms and 600 cm⁻¹ for the quartic terms, Table 4. In both systems, the analyzed modes are strongly coupled to in-plane bending motion (δ_OH and δ_OHO) and out-of-plane bending motion (γ_OH and γ_OHO). Asymmetric O⋯H⋯O motion is additionally modified by the low frequency ν_OO mode that adjusts the distance between the oxygen atoms, and also by C=O and C=C stretching modes (ν_CO and ν_CC, those two modes are shown on Fig. 4). Figures of all those normal modes are provided in the ESI, Fig. S2.† According to the results presented in Table 4, a 3D and a 6D model should be constructed for the A and S conformer, respectively. The 3D model would comprise ν_OH, δ_OH and γ_OH, whereas a 6D model would be built from ν^a_OHO, δ_OHO, γ_OHO, ν_OO, ν_CO and ν_CC. Construction of these high-dimensional models would require significant computational time. Therefore, in order to assess the influence of each mode on the mode of interest, we first analyzed 2D models.

Table 4 Absolute values of cubic anharmonic force constants larger than 500 cm⁻¹ and quartic anharmonic force constants larger than 600 cm⁻¹ that describe coupling of ν_OH and ν^a_OHO with other vibrational degrees of freedom

A
KνOHγOHγOH	989
KνOHνOHδOH	703
KνOHνOHγOHγOH	1071

---

S
	685
	560
	1773
	866
	650

---

The 2D potential energy surfaces are depicted on Fig. 5. Let us first analyze the results for the A structure. The potential spanned by O–H stretch and O–H in-plane bend is presented on Panel A. The global minimum corresponds to the origin of the coordinate system, whereas the local minimum describes a situation when the hydrogen atom forms a covalent bond with the atom O₂. As discussed previously, the potential is not symmetric because the reference structure is the stable structure with covalent O₁H bond. The ground state wavefunction is located in the global minimum. On the other hand, the potential energy surface of the O–H stretch and O–H out-of-plane bend V(Q_νOH, Q_γOH), Panel B, is marked by a single minimum, since out-of plane bend shifts the active hydrogen atom away from both oxygen atoms.

Fig. 5 2D potential energy surfaces up to 8000 cm⁻¹, with contour spacing of 500 cm⁻¹ (grid dimensions in ). Surfaces presented on Panels (A) and (B) are obtained for the A species, whereas surfaces shown on Panels (C)–(F) correspond to the S conformer. (A) V(Q_νOH, Q_δOH). (B) V(Q_νOH, Q_γOH). (C) V(Q_ν^aOHO, Q_δOHO). (D) V(Q_ν^aOHO, Q_γOHO). (E) V(Q_ν^aOHO, Q_νOO). (F) V(Q_ν^aOHO, Q_νCO).

We will now take a closer look at potentials of the symmetric structure. Motion along the mode brings the hydrogen atom closer to either of the oxygen atoms, allowing a covalent bond to be formed, which explains a double minimum shape (the two minima are identical). Interestingly, in all five cases, the lowest energy vibrational level is positioned above the top of the barrier, resulting in delocalized wavefunctions of the ground states. The potentials (Panel C) and (Panel E) posses a mirror plane, whereas potentials (Panel F) and posses center of inversion. The potential is not depicted, but is qualitatively identical to 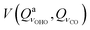. The most interesting coupling is the one between O⋯H⋯O stretch and out-of-plane bend, Panel D. Simultaneous change of the two coordinates by the same amount (regardless of the sign) leads to a slow rise of the potential, giving it a remarkable shape.

The ν_OH and ν^a_OHO frequencies within 2D approximation were also computed with the Lanczos–Arnoldi method (cf. Section 3.3.1). They are compiled in Table 5. Coupling between ν_OH and δ_OH/γ_OH leads to a shift of −254/47 cm⁻¹ with respect to 1D frequency, resulting in 2366/2667 cm⁻¹. This means that the O–H stretching frequency within a 3D model (that includes ν_OH, δ_OH and γ_OH) would be located in the range 2300–2700 cm⁻¹, a region that is completely empty in the experimental spectrum.⁷⁶ This is in accord with the results presented in Section 3.3 that predict extremely low intensity of the ν_OH peak.

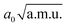Table 5 Modes that comprise 2D models (grid dimensions in ), anharmonic ν_OH and ν^a_OHO frequencies (in cm⁻¹) computed within 2D approximation, and differences between 2D and 1D frequencies Δν_OH(O) = ν^2D_OH(O) − ν^1D_OH(O) (in cm⁻¹). 45 grid points were used along each mode

Mode (grid)	Mode (grid)	ν^2DOH	ΔνOH
A
νOH (−2.00/0.50)	δOH (−1.70/1.00)	2366	−254
νOH (−1.00/1.00)	γOH (−1.50/1.50)	2667	47

---

Mode (grid)	Mode (grid)	ν^a,2DOHO	Δν^aOHO
S
ν^aOHO (−1.30/1.30)	δOHO (−1.00/0.80)	808	−123
ν^aOHO (−1.70/1.70)	γOHO (−1.70/1.70)	843	−88
ν^aOHO (−1.00/1.00)	νOO (−1.90/2.30)	801	−130
ν^aOHO (−1.00/1.00)	νCO (−1.00/1.00)	842	−89
ν^aOHO (−0.90/0.90)	νCC (−0.90/0.90)	909	−22

---

We will proceed with analysis of 2D results for the S structure. Interaction with all five modes redshifts the ν^a_OHO frequency. The strongest influence on ν^a_OHO have δ_OHO and ν_OO, that lower the frequency by 123/130 cm⁻¹. γ_OHO and ν_CO have less influence on ν^a_OHO (88 and 89 cm⁻¹, respectively), whereas coupling to ν_CC changes the frequency by only 22 cm⁻¹. These results enable construction of more complex models for DBM, that could unravel the position of the O⋯H⋯O stretching frequency.

3.3.3 3D models. In order to locate the position of ν^a_OHO in DBM, it would be desirable to constructed a 5D model that would comprise ν^a_OHO, δ_OHO, γ_OHO, ν_OO and ν_CO, according to Table 5. However, computation of a 5D grid would require substantial amount of computational time, and we are forced to search for a less demanding procedure. Thus, we included modes that have the strongest impact on the mode of interest and computed a 3D potential V(ν^a_OHO, δ_OHO, ν_OO). A 75 × 45 × 45 grid in the range −1.30 ≤ ≤ 1.30 , −1.90 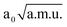≤ Q_δOHO ≤ 2.40 and −1.30 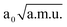≤ Q_νOO ≤ 1.30 was used. The IR spectrum was calculated with the MCTDH program.³⁸ Four single-particle functions were used per each degree of freedom. Each single-particle function was expanded using a fast Fourier transform primitive basis representation. Since motion of the active hydrogen takes place along the x-axis (cf. Fig. 2), we used the x component of the dipole moment along each normal mode. The IR spectrum was computed by propagating the wavefunction for 1 ps, and performing a Fourier transform of the dipole auto-correlation function, as implemented in the MCTDH program package.⁷³ First, it was necessary to generate the initial wavefunction. As an initial wavefunction, we used the eigenfunction of the 3D potential energy surface, which was generated by propagation of a guess function in imaginary time.^73,77 In order to compute the IR spectrum, propagation of the wavefunction was performed with the variable mean-field method using the Adams–Bashforth–Moulton predictor–corrector integrator of sixth-order with an error tolerance of 10⁻⁷. The initial step size was set to 0.01 fs. Position of the O⋯H⋯O stretching frequency within this 3D model is computed to be only 673 cm⁻¹. The experimental⁷⁶ and the 3D theoretical spectrum are depicted on Fig. 6.

Fig. 6 Experimental infrared spectrum⁷⁶ of DBM and the theoretical spectrum (vertically off-set) computed within a 3D model that comprises , Q_δOHO and Q_νOO. Absorbance of both spectra is given in arbitrary units. The experimental spectrum is reproduced with permission from National Institute of Standards and Technology.

It is interesting to note that according to the computed anharmonic terms, coupling between in-plane and out-of-plane bend is weak, and also there are no important anharmonic force fields that simultaneously mix the three terms. For this reason, the result obtained with a 3D potential computed on the grid could have been anticipated from the 2D results: by adding contributions from the two modes (cf. Table 5), one would expect the antisymmetric O⋯H⋯O band to be located around 678 cm⁻¹(931 − 123 − 130), which differs by only 5 cm⁻¹ from the 3D value. This means that if couplings among other degrees of freedom are weak, this procedure could be used for obtaining approximate anharmonic frequencies that would have been obtained with a model of higher dimensionality. In order to verify the above statement, we computed a 3D potential that describes interaction between O⋯H⋯O stretch and the other two modes, V(ν^a_OHO, γ_OHO, ν_OO). For this system, the ν^a_OHO band is expected to appear around 931 − 88 − 89 = 754 cm⁻¹. A potential on a 75 × 45 × 45 grid in the range −2.50 ≤ ≤ 2.50 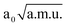, −2.80 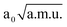≤ Q_γOHO ≤ 2.80 and −1.40 ≤ Q_νCO ≤ 1.40 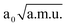was used. The position of the O⋯H⋯O stretching band is located at 789 cm⁻¹, that differs by 35 cm⁻¹ from approximated 754 cm⁻¹. This allows us to predict the ν^a_OHO value within a 5D model, since couplings among modes δ_OHO, γ_OHO, ν_OO and ν_CO are also weak (absolute values of all cubic and quartic terms are lower than 200 cm⁻¹): 931 − 258 − 142 = 531 cm⁻¹ (258 and 142 cm⁻¹ are red shifts of the mode of interest within the two 3D models with respect to a 1D model). Therefore, the estimated value of the O⋯H⋯O stretching frequency is close to 500 cm⁻¹. Applying the same procedure to the A conformer (there are no large anharmonic terms that simultaneously couple ν^a_OHO with in- and out-of-plane bend), the ν^a_OHO frequency within a 3D model (ν^a_OHO, δ_OHO and γ_OHO) can be estimated from 1D and 2D values: 2620 − 254 + 47 = 2413 cm⁻¹.

The predicted value for ν^a_OHO frequency is not surprising if compared to similar systems. One of the most investigated systems with a symmetric O⋯H⋯O motif is hydrogen maleate ion, that has in the last few decades been thoroughly investigated both experimentally and theoretically.^78–82 This ion is known to have symmetric form both in the gas and in the solid phase, as well as in a solution. The experimental bands of the IR spectrum of potassium hydrogen maleate ion in solution⁷⁸ were assigned by gas phase calculations:⁷⁹ two modes were found to have predominant OHO asymmetric stretching character, at 540 and at 700 cm⁻¹. This is a floppy system, so mode mixing is very pronounced. Recent theoretical analysis of potassium hydrogen maleate in the solid state⁸⁰ revealed the peaks that involve ν^a_OHO to appear at 397 and 449 cm⁻¹. Thus, theoretical calculations predict the ν^a_OHO frequency of potassium hydrogen maleate in the gas and solid state, and also in solution to be located in the range 400–700 cm⁻¹.

4 Structural parameters of the two conformers revisited

Although the symmetry of the hydrogen maleate ion is the same in gas and solid state and also in solution, that is not the case with its fluorinated counterpart – it has recently been shown⁸³ that difluoromaleate monoanion is symmetric in the solid state, and asymmetric in solution, i.e. local environment governs the symmetry of this system. On the other hand, our results predict that DBM is at room temperature present both in the symmetric and in the asymmetric form. Since it was shown that analysis of both conformers represents a multidimensional problem, we can predict what the S structure looks like within anharmonic picture. In both 3D models, the equilibrium value of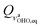 coordinate (subscript eq is used to label the values that correspond to the ground state vibrational wavefunctions obtained with the procedure described in Section 3.3.3) is equal to zero, while the other four modes are mutually only weakly coupled (cf. Tables S4 and S6 in the ESI†). If we displace the optimized structure along the other four coordinates according to their equilibrium 3D values (0.183, 0.284, 0.227 and 0.192 for Q_δOHO,eq, Q_νOO,eq, Q_γOHO,eq and Q_νCO,eq, respectively), we arrive at the structure with O–O distance of 2.361 Å, while the O₁–H and O₂–H distances amount to 1.215 Å and 1.202 Å, i.e. a structure that we referred to as a symmetric structure actually represents a weakly asymmetric system. The slight asymmetry is predominantly due to coupling to the asymmetric CO stretching mode displayed in Fig. 4. Analogously, we can arrive at the equilibrium structure of the A species within a 3D model starting from equilibrium 2D values (equilibrium values for Q_νOH,eq within 2D models is −0.057 and −0.032 , which gives displacements of −0.089, −0.048 and −0.001 for Q_νOH,eq, Q_δOH,eq and Q_γOH,eq, respectively), O₁–H and O₂–H distances are 1.060 Å and 1.517 Å, respectively. Therefore, taking into account multidimensionality of hydrogen bond potential energy surface, we find that the O₁–H and O₂–H bonds elongate by 0.051 and 0.041 Å (A structure), 0.014 and 0.001 Å (S structure) in comparison with minimum energy structures.

5 Conclusions

Part of the potential energy hyper-surface of gas phase dibenzoylmethane (enol form) with hydrogen atom between the oxygen atoms is characterized with two identical minima (asymmetric structures) and a transition state that connects them. According to simple geometry optimization, one would assume that this molecule is characterized with an asymmetric O–H⋯O fragment. However, inclusion of zero point energy predicts the symmetric structure to be more stable according to B3LYP, M06-2X, MP2, SCS-CC2 and CC2 results (this is also the case with the Gibbs free energy), whereas G4MP2 predicts the asymmetric structure to be more stable. Both species are present in the gas phase at room temperature. Analysis of electron density and its topological properties at the bond critical points revealed substantial covalent character of HB in symmetric form of DBM, whereas the asymmetric molecule represents a typical hydrogen bonded system. Moreover, our models in reduced dimensionality show that structural parameters of the OHO fragment change upon inclusion of mode couplings. The O–H stretching frequency of the asymmetric conformer amounts to approximately 2400 cm⁻¹ with negligible IR intensity (as obtained by calculations that include electrical anharmonicity), which is reflected in the absence of the corresponding band in the experimental IR spectrum. The position of the O⋯H⋯O asymmetric stretching frequency is estimated to be close to 500 cm⁻¹.

Acknowledgements

This work was financially supported by the Ministry of Education and Science of Republic of Serbia within the framework of the project 172040. Numerical results were obtained on the PARADOX cluster at the Scientific Computing Laboratory of the Institute of Physics Belgrade, supported in part by the Serbian Ministry of Education, Science and Technological Development under projects No. ON171017 and III43007, and by the European Commission under FP7 project PRACE-3IP. The authors thank the anonymous referees for their suggestions that helped in improving the quality of the paper. M.P. is grateful to U. Andjelić for performing preliminary calculations.

References

1. F. Wetz, C. Routaboul, D. Lavabre, J.-C. Garrigues, I. Rico-Lattes, I. Pernet and A. Denis, Photochem. Photobiol., 2004, 80, 316–321.
2. M.-T. Huang, Y.-R. Lou, J. G. Xie, W. Ma, Y.-P. Lu, P. Yen, B. T. Zhu, H. Newmark and C.-T. Ho, Carcinogenesis, 1998, 19, 1697–1700.
3. F. Dumur, M. Lepeltier, H. Z. Siboni, P. Xiao, B. Graff, J. Lalevée, D. Gigmes and H. Aziz, J. Lumin., 2014, 151, 34–40.
4. F. T. Wall and W. F. Claussen, J. Am. Chem. Soc., 1939, 61, 2812–2815.
5. J. L. Burdett and M. T. Rogers, J. Am. Chem. Soc., 1964, 86, 2105–2109.
6. G. Allen and R. A. Dwek, J. Chem. Soc. B, 1966, 1, 161–163.
7. R. L. Lintvedt and H. F. Holtzclaw Jr, J. Am. Chem. Soc., 1966, 88, 2713–2716.
8. H. Morita and H. Nakanishi, Bull. Chem. Soc. Jpn., 1981, 54, 378–386.
9. M. Bassetti, G. Cerichelli and B. Floris, Tetrahedron, 1988, 44, 2997–3004.
10. E. V. Borisov, E. V. Skorodumov, V. M. Pachevskaya and P. E. Hansen, Magn. Reson. Chem., 2005, 43, 992–998.
11. J. R. B. Gomes and M. A. V. R. da Silva, J. Phys. Chem. A, 2006, 110, 13948–13955.
12. N. V. Belova, H. Oberhammer and G. V. Girichev, Struct. Chem., 2011, 22, 269–277.
13. D. E. Williams, Acta Crystallogr., 1966, 21, 340–349.
14. R. D. G. Jones, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 1807–1811.
15. S. F. Tayyari, H. Rahemi, A. Nekoei, M. Zahedi-Tabrizi and Y. A. Wang, Spectrochim. Acta, Part A, 2007, 66, 394–404.
16. F. J. Hollander, D. H. Templeton and A. Zalkin, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 1552–1553.
17. B. Kaitner and E. Meštrović, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1993, 49, 1523–1525.
18. P. Gilli, V. Bertolasi, L. Pretto, V. Ferretti and G. Gilli, J. Am. Chem. Soc., 2004, 126, 3845–3855.
19. L. H. Thomas, A. J. Florence and C. C. Wilson, New J. Chem., 2009, 33, 2486–2490.
20. M. J. Frisch, et al., Gaussian 09 Revision D.01, Gaussian Inc.Wallingford, CT 2009.
21. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
22. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
23. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
24. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023.
25. R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
26. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
27. M. Head-Gordon and T. Head-Gordon, Chem. Phys. Lett., 1994, 220, 122–128.
28. TURBOMOLE V6.5 2013, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, http://www.turbomole.com.
29. A. Hellweg, S. A. Grün and C. Hättig, Phys. Chem. Chem. Phys., 2008, 10, 4119–4127.
30. C. Hättig, J. Chem. Phys., 2003, 118, 7751–7761.
31. C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154.
32. D. Feller, J. Comput. Chem., 1996, 17, 1571–1586.
33. K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052.
34. L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 127, 124105.
35. J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218.
36. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
37. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
38. G. A. Worth, M. H. Beck, A. Jäckle and H.-D. Meyer, The MCTDH Package, Version 8.2, (2000). H.-D. Meyer, Version 8.3 (2002), Version 8.4 (2007), http://mctdh.uni-hd.de.
39. M. Petković, J. Novak and N. Došlić, Chem. Phys. Lett., 2009, 474, 248–252.
40. I. Matanović, N. Došlić and Z. Mihalić, Chem. Phys., 2004, 306, 201–207.
41. J. Antony, G. von Helden, G. Meijer and B. Schmidt, J. Chem. Phys., 2005, 123, 014305.
42. K. Giese, M. Petković, H. Naundorf and O. Kühn, Phys. Rep., 2006, 430, 211–276.
43. M. Torrent-Sucarrat, J. M. Anglada and J. M. Luis, Phys. Chem. Chem. Phys., 2009, 11, 6377–6388.
44. R. Vianello and J. Mavri, New J. Chem., 2012, 36, 954–962.
45. V. Jovanović, Y. Miyazaki, T. Ebata and M. Petković, J. Phys. Chem. A, 2013, 117, 6474–6482.
46. R. Cuypers, E. J. R. Sudhölter and H. Zuilhof, ChemPhysChem, 2010, 11, 2230–2240.
47. M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, J. Phys. Chem. A, 2013, 117, 12590–12600.
48. S. J. Grabowski, J. Phys. Org. Chem., 2004, 17, 18–31.
49. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, 1990.
50. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
51. I. Mata, I. Alkorta, E. Espinosa and E. Molins, Chem. Phys. Lett., 2011, 507, 185–189.
52. T. Y. Nikolaienko, L. A. Bulavina and D. M. Hovorun, Phys. Chem. Chem. Phys., 2012, 14, 7441–7447.
53. P. Atkins and J. de Paula, Physical Chemistry, Oxford University Press, 8th edn, 2006.
54. B. K. Paul and N. Guchhait, Chem. Phys., 2013, 412, 58–67.
55. R. W. Gora, S. J. Grabowski and J. Leszczynski, J. Phys. Chem. A, 2005, 109, 6397–6405.
56. W. Zhuang, T. Hayashi and S. Mukamel, Angew. Chem., Int. Ed., 2009, 48, 3750–3781.
57. T. Elsaesser, Acc. Chem. Res., 2009, 42, 1220–1228.
58. B. Czarnik-Matusewicz, M. Rospenk, A. Koll and J. Mavri, J. Phys. Chem. A, 2005, 109, 2317–2324.
59. J. Mavri and J. Grdadolnik, J. Phys. Chem. A, 2001, 105, 2039–2044.
60. J. Stare, J. Panek, J. Eckert, J. Grdadolnik, J. Mavri and D. Hadži, J. Phys. Chem. A, 2008, 112, 1576–1586.
61. B. Kojić-Prodić and K. Molčanov, Acta Chim. Slov., 2008, 55, 692–708.
62. M. Petković and O. Kühn, J. Phys. Chem. A, 2003, 107, 8458–8466.
63. M. Petković and O. Kühn, Chem. Phys., 2004, 304, 91–102.
64. M. Petković, J. Phys. Chem. A, 2012, 116, 364–371.
65. Y. Miyazaki, Y. Inokuchi, T. Ebata and M. Petković, Chem. Phys., 2013, 419, 205–211.
66. G. Peinel, Chem. Phys. Lett., 1979, 65, 324–326.
67. V. Barone, J. Chem. Phys., 2004, 120, 3059–3065.
68. V. Barone, J. Chem. Phys., 2005, 122, 014108.
69. V. Barone, J. Bloino, C. A. Guido and F. Lipparini, Chem. Phys. Lett., 2010, 496, 157–161.
70. W. E. Arnoldi, Q. Appl. Math., 1951, 9, 17–29.
71. Y. Saad, Lin. Algebra. Appl., 1980, 34, 269–295.
72. R. A. Friesner, L. S. Tuckerman, B. C. Dornblaser and T. V. Russo, J. Sci. Comput., 1989, 4, 327–354.
73. M. H. Beck, A. Jäckle, G. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105.
74. J. M. Hollas, Modern Spectroscopy, John Wiley & Sons Ltd, 4th edn, 2004.
75. M. Petković, Chem. Phys., 2007, 331, 438–446.
76. “Infrared Spectra” in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, NIST Mass Spec Data Center, S.E. Stein, director, National Institute of Standards and Technology, Gaithersburg MD, 20899,http://webbook.nist.gov, retrieved April 3, 2014.
77. R. Kosloff and H. Tal-Ezer, Chem. Phys. Lett., 1986, 127, 223–230.
78. F. Avbelj, B. Orel, M. Klanjšek and D. Hadži, Spectrochim. Acta, Part A, 1985, 41, 75–87.
79. F. Avbelj, M. Hodošček and D. Hadži, Spectrochim. Acta, Part A, 1985, 41, 89–97.
80. M. V. Vener, A. V. Manaev, D. Hadži and V. G. Tsirelson, Z. Physiol. Chem., 2008, 222, 1349–1358.
81. M. M. Ilczyszyn, J. Baran, H. Ratajczak and A. J. Barnes, J. Mol. Struct., 1992, 270, 499–515.
82. F. Fillaux, N. Leygue, J. Tomkinson, A. Cousson and W. Paulus, Chem. Phys., 1999, 244, 387–403.
83. C. L. Perrin, P. Karri, C. Moore and A. L. Rheingold, J. Am. Chem. Soc., 2012, 134, 7766–7772.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra05586a

---