Enforced conformational changes in the structural units of glycosaminoglycan (non-sulfated heparin-based oligosaccharides)

Abstract

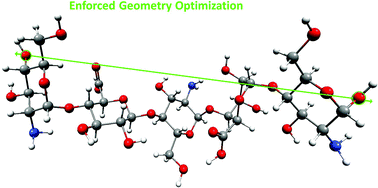
The conformational transitions in the structural units of glycosaminoglycans (GAGs) were the subject of many theoretical and experimental studies. However, relatively little is known about the mechanism of enforced structural changes that occur simultaneously in the individual components in the slightly longer fragments (oligomers) of GAGs. The complex molecular structure of mucopolysaccharides makes the correct interpretation of the AFM single molecule experiments quite complicated. Such information can be mainly obtained by theoretical methods. This paper reports the results of the Enforced Geometry Optimization (EGO) simulations of enforced structural changes in the monomeric units and selected dimeric: α-L-iduronic acid (1 → 4) α-D-glucosamine (IdoA-GlcN), β-D-glucuronic acid (1 → 4) α-D-glucosamine (GluA-GlcN), and pentameric GlcN-IdoA-GlcN-GluA-GlcN non-sulfated heparin-based oligomers. We present the theoretical analysis of the possible enforced conformational transitions.

---

Introduction

The mechanical stability and conformational flexibility of molecules under external forces play unquestionable roles in nature, particularly in biologically important molecular systems.

Atomic force microscopy (AFM) is a relevant method to explore such properties at single molecule level. However, proper interpretation of experimental AFM force-extension curves can be difficult and still challenging. Not every plateau corresponds to conformational transitions/dramatic structural changes and not every transition can be clearly seen even for homopolymers that contain only a single type of repeating unit. The situation becomes more complicated for heteropolymers derived from at least two monomeric species. In this case, different conformational transitions can take place under the same external force and it can be manifested on the force-extension curve in different ways. Molecular insights on the origins of mechanical responses can be inferred from simulations based on theoretical methods.

In this study we investigate the possible enforced conformational changes in the non-sulfated heparin-based oligomers. Because of its biological importance, clinical applications and specific properties, the heparin structure has been studied extensively, both theoretically^1–12 and experimentally.^13–21 Glycosaminoglycan heparin is an unbranched heteropolysaccharide composed of two types of repeating units (dimers).¹³ The first disaccharide unit (called here dimer A) consist of α-L-iduronic acid (IdoA) and α-D-glucosamine (GlcN) saccharides connected by the 1 → 4 linkage. The second one (called here dimer B) is made up of 1 → 4-linked β-D-glucuronic acid (GlcA) and α-D-GlcN monosaccharides (the ratio of these dimers in heparin is about as 8 : 2).¹³ IdoA and GlcN units can be substituted by O- or N-sulfated groups. It should be emphasized that, the most of the anti-coagulant activity of heparin is associated with the unique pentasaccharide sequence: GlcN-IdoA-GlcN-GluA-GlcN.^22,23

The AFM experiment¹³ shows that external stretching forces applied to the terminal glycosidic oxygen atoms of heparin induce conformational transition(s). The plateau at ∼200 pN observed on the force-extension curves is characteristic for 1 → 4 linkages between the pyranose monomers^13,24 with the glycosidic/aglycone bond in the axial orientation(s). However, because of relatively complicated molecular structure of heparin (three different saccharide units: IdoA, GlcN and GlcA), the unequivocal assignment of this plateau to a specific conformational transition is quite difficult.

This paper presents a theoretical description of the structural changes in non-sulfated heparin-based oligosaccharides induced by the external stretching forces. We examine the neutral (non-ionized) and non-sulfated monomeric (IdoA, GlcN, GlcA) components of heparin as well as its dimeric (IdoA-GlcN, GlcN-GlcA) and pentameric (GlcN-IdoA-GlcN-GluA-GlcN) oligomers.

We report results from the Enforced Geometry Optimization (EGO)^25–28 simulations of structural changes induced by external stretching forces applied to the two terminal glycosidic oxygen atoms (O1 and O4). The molecular systems considered here and the external force action mode are depicted in Fig. 1.

Fig. 1 The molecular systems and the stretching force modes. The superscripts a and e denote the axial and equatorial position of the terminal –OH groups. The characteristic glycosidic torsion angles are defined as: ψ = H1C1O1^gC2, Φ = C1O1^gC2H2.

Computational details

The theoretical simulations of AFM experiments provide the qualitative and quantitative information about the mechanical properties of biological and/or synthetic macromolecules. These simulations can be performed via several distinct methodologies. The most widely used method is the molecular dynamic which simulates the AFM experiments through methodology called Steered Molecular Dynamics (SMD)²⁹ or Potential of Mean Force (PMF) molecular dynamics.³⁰

The mechanical properties of individual units of the polymers can be also described by quantum mechanics-based methods. The most popular, i.e. geometry optimization with some constrains (CGO) can simulate the external forces acting on the selected atoms in a molecule. This approach allows to estimate energy differences (energy barrier) between stretched (extended) and relaxed forms. Such energy profiles can be also correlated with the experimental force-extension curves. However, the typical constrained geometry optimization may sometimes introduce some artifacts resulting from poor realistic response of the molecule. Alternative, recently proposed the EGO approach is a simple quantum chemical model which can be successfully used to simulate the effect of the external forces acting on a single molecule. It involves optimizing the geometry of a molecule with an external force applied to selected nuclei. This allows to simulate a response of the molecule to external forces in a more physical (realistic) way.

Up to now, the EGO model has been efficiently applied for: (i) investigating conformational transitions in (poly)saccharide molecules; (ii) generating potentially new structural isomers^27,28 (iii) locating transition state²⁶/examining chemical pathways and alternative reaction mechanisms.

The basic idea behind the EGO model is to perform geometry optimization in the presence of external forces acting on selected nuclei in a molecule. When an external force f_A is applied to a given nucleus A at the position R_A then the interaction energy of a molecule with that external force field is defined as

E_A = −R_A·f_A (1)

The total energy of a molecule with external forces acting on a number of selected nuclei is given as:

where E is the molecular energy without external forces. Such definition of the total energy (2) ensures consistency between that energy and the total forces on atoms:

F_A = −dE_total/dR_A = −dE/dR_A + f_A (3)

where the first term in (3) is just the standard force on nucleus A at the given molecular geometry (zero when equilibrium). The equilibrium geometry of a system in the presence of external forces is determined by the usual condition of vanishing forces (3) on atoms:

F_A = 0 → dE/dR_A = f_A for each nucleus A (4)

The last equation shows that a molecule has to change its geometry in order to generate an internal force on atom A which will cancel an applied external force.

In practice, in the EGO model an additional gradient for selected nuclei is added to the standard gradient calculated for a whole molecule at a given geometry. Since the total gradient vector, not energy, is the primary factor which determines any geometry optimization algorithm, it does not really matter if the interaction energy term (1) is included in the EGO calculations or not: in both cases the geometry optimization will proceed in the same way. Inclusion of this term ensures consistency of the total energy with its gradient. However, for energy comparisons with structures obtained without external forces it is more convenient to leave this term out. In this paper all reported energies do not include this term.

The external forces can be applied to an arbitrary number of nuclei and in fully arbitrary directions. However, in practice we apply the external force to two atoms along a line joining pairs of atoms in a molecule, either as a “push” (to push the two atoms together – squeezing mode) or as a “pull” (to pull them apart – stretching mode). Thus, there is no translation or rotation of a molecule.

In this study we investigate structural changes caused by external stretching forces applied to two terminal oxygen atoms O1 and O4 of chain/molecule (potential location of glycosidic bonds). As mentioned above, three monomeric neutral and non-sulfated heparin-based saccharides (IdoA, GlcN and GlcA) are considered. Additionally, we analyze two dimeric structures – denoted above as dimer A (IdoA-GlcN) and dimer B (GlcN-GlcA) and the selected pentameric sequence of heparin (GlcN-IdoA-GlcN-GluA-GlcN). Two monosaccharides: GlcA and GlcN exist in the ⁴C₁ conformation within the heparin chain, whereas the IdoA molecule oscillates between its chair (¹C₄) and skew boat (²S₀) conformations without the significant conformational change in the backbone.³¹ In this study both conformers (⁴C₁ and ²S₀) of α-L-iduronic acid present in the considered structures are taken into account.

In order to distinguish among the different possible glycopyranose ring conformations we use the endo-cyclic torsion angles: τ₁ = ∠C1C2C3C4, τ₂ = ∠C2C3C4C5 and τ₃ = ∠C3C4C5O6 according to Bérces et al.³² This allows us to determine a particular pucker and express it in terms of the closest matching chair, boat or twisted boat conformations. We also report the molecule length defined as the distance between the distinctive oxygen atoms (O4^a, O1^a and O^g) of the stretched (stressed) and corresponding relaxed structures.

The NMR studies³³ indicate that the conformation of heparin molecule in solution is very similar to its solid state conformation.^34,35 The structure of a heparin has been determined using a combination of NMR spectroscopy and molecular modeling techniques by Mulloy et al.³⁶ Heparin has well-defined molecular structure in terms of overall chain conformation with subtle differences arising from the conformational versatility of the pyranose ring of iduronic acid (two models: (1) IdoA units with ²S₀ conformation, (2) IdoA units with ¹C₄ conformation). Therefore, the starting oligomeric structures of non-sulfated heparin-based oligosaccharides were built using the initial coordinates taken from the study performed by Mulloy et al.³⁶

The optimized ground state geometries were exposed to external stretching forces, usually in the range of from 0.02 to 0.075 au in steps of 0.0005/0.00025 au (1 au = 82 387.2 pN). The stressed structures after the EGO procedure were relaxed, i.e. re-optimized in the absence of any external forces. The relaxation process allows to determine whether or not the structural changes (conformational transition(s), changes in glycosidic linkage(s) etc.) induced by the external tensile forces are permanent. For each resulting relaxed structure vibrational analysis was carried out to confirm its stability.

The results reported here were obtained at the B3LYP/6-31G(d,p) level of theory. All calculations were performed in parallel with the PQS program package and structural changes visualized and analyzed using the graphical interface program PQSMol.³⁷

The standard and enforced geometry optimization procedures were performed with the default convergence criteria on the gradient, geometry displacement and energy change values, predefined in PQS package.

Results and discussion

Generally, the force induced conformational transitions can be observed in polysaccharides with the axially linked monomer units.^13,24 In the starting ¹C₄ IdoA^c conformer considered here, both (glycosidic and aglycone) bonds are in the axial orientation. In the case of ⁴C₁ GlcN conformer only one (glycosidic) bond is axially oriented while for ⁴C₁ GlcA saccharide both the aglycone and glycosidic bonds are in the equatorial position.

Monomeric structures

Iduronic acid. It has been proved that α-L-iduronic acid plays the crucial role in intermolecular interaction of heparin with proteins. This results from its unique conformational flexibility. As mentioned above, IdoA monosaccharide exists either in the ¹C₄ chair or in the ²S₀ skewed boat conformers, in 8 : 2 ratio.³⁸ The energy barrier between the ¹C₄ and ²S₀ conformations is relatively low and the oscillation between these two conformations is rapid. IdoA can adopt any of these two conformations or even both, when present in oligosaccharides complexed with their protein receptors.¹⁵

In order to describe structural changes in considered molecules, we analyze the stretched/relaxed energy profiles (i.e. energy vs. applied force). These profiles for both conformers are shown in Fig. 2. Applying forces less than 0.03 au for IdoA^c (⁴C₁) and less than 0.0375 au for IdoA^s (²S₀) conformer does not cause any permanent structural changes in molecules. Their pyranose rings are slightly deformed, but the relaxation process after the EGO optimization brings them back to the starting stable structures. The structural changes in molecules are manifested by the rapid energy shifts. For IdoA^c conformer one can observe two jumps/triggers (at forces: 0.03 au and 0.0625 au). Thus there are two conformational transitions

Fig. 2 Energy of stretched (forced) and corresponding relaxed monomers (a) IdoA^c and (b) IdoA^s as a function of applied external force. The selected stretched/relaxed structures are presented in blue/red frames.

• ¹C₄ → ⁰S₂ for forces 0.030 au ≤ f ≤ 0.0625 au.

• direct conversion ¹C₄ → ⁴C₁ for forces 0.0625 au ≤ f ≤ 0.075.

Note that, the maximum elongation exceeds 1.5 Å, i.e. almost 35% of the initial length of the molecule. Moreover, the enforced geometry optimization results in the reorientation of the hydroxyl groups in positions 1 and 4 of the saccharide ring from equatorial to axial. Applying force greater than 0.075 au causes the irreversible degradation of the structure.

The skew-boat IdoA^s conformer directly goes into the chair conformation (⁴C₁) for external stretching force greater than 0.0375 au. Similarly, the permanent degradation of the structure occurs at forces greater than 0.075 au.

The theoretical force-extension curves – i.e. external stretching force vs., elongated molecule length – depicted in Fig. 3 are consistent with the stretched/relaxed energy profiles for IdoA^c and IdoA^s structures.

Fig. 3 Theoretical force-extension curves (i.e. external stretching force vs. elongated molecule length) for IdoA^c and IdoA^s monomers.

According to the procedure (for assessing physical data in terms of sterically accessible iduronate conformers) adopted by Ernst et al.,^{39 1}C₄ conformer could interchange with ⁰S₂ (and ³S₁) form(s), while ⁴C₁ could convert into ²S₀ (and ³S₁) form(s). The enforced conformational changes in the iduronic acid ring discussed above are consistent with these results.

Glucuronic acid and glucosamine. The theoretical stretched/relaxed energy profiles for glucuronic acid and glucosamine monomers are presented in Fig. 4.

Fig. 4 Energy of stretched (forced) and corresponding relaxed monomers: (a) GlcA and (b) GlcN as a function of applied external force. The selected stretched/relaxed structures are presented in blue/red frames.

As mentioned above GlcA does not have the axially oriented O4H and O1H groups. Therefore, the stretching/relaxed profile for GlcA does not display any distinctive permanent conformational changes and the relaxation process leads back to the starting monomeric structure with the ¹C₄ conformation. The maximum elongation of GlcA molecule is about 0.75 Å (∼15% of initial molecule length).

In the case of the monomeric glucosamine structure, applying the stretching force greater than 0.0275 au causes the direct ⁴C₁ → ¹S₃ flip. This conformational transition is also manifested in the theoretical force-extension curve (see Fig. 5). The irreversible degradation of monomeric structures (GlcN and GlcA) occurs when the external stretching force is greater than 0.075 au.

The EGO description of the enforced structural changes in the saccharide monomers (IdoA, GlcN and GlcA) are consistent with the theoretical (constrained geometry optimization) results obtained by Marszalek et al.¹³

Fig. 5 Theoretical force-extension curves (i.e. external stretching force vs. elongated molecule length) for GlcN and GlcA monomers.

Dimeric structures

The structural responses of the relevant heparin-based disaccharide units (dimer A and dimer B) to the external forces are more complicated. This can be seen from the stretched/relaxed energy profiles and the theoretical force-extension curves shown in Fig. 6 and 7.

Fig. 6 Energy of stretched (forced) and corresponding relaxed dimeric structures: (a) dimer A IdoA^c-GlcN, (b) dimer A IdoA^s-GlcN and (c) dimer B as a function of applied external force.

Fig. 7 Theoretical force-extension curves (i.e. external stretching force vs. elongated molecule length) for dimers A and dimer B.

IdoA^c-GlcN (dimer A). The application of a stretching force less than 0.03 au to the terminal glycosidic oxygen atoms of the dimer A (IdoA^c-GlcN) does not cause any conformational changes. The relaxation process yields in this case the starting structure (the range denoted as ① in Fig. 6). The next narrow region in the stretched/relaxed energy profile (labeled ②) corresponds to the conformational transition ¹C₄ → ⁰S₂ in iduronic acid unit whereas glucosamine unit remains unchanged (with ⁴C₁ conformation). Upon the stretching force 0.035 ≤ f ≤ 0.0425 au one can observe the subsequent structural changes in both saccharide units, i.e. ¹C₄ → ⁰S₂ in iduronic acid monomer and ⁴C₁ → ¹S₃ in glucosamine monomer. The application of a stretching force greater than 0.045 au flips both pyranose rings: from ¹C₄ to ⁴C₁ conformation of the IdoA unit and from ⁴C₁ to ¹S₃ conformation of the GlcN unit. These transitions cause the increase in the dimer molecule length from 8.956 Å to 10.713 Å for the maximum stretching force f = 0.07 au (20% of the starting molecular length). During the enforced geometry optimization the reorientation of the saccharide units is also observed. This intramolecular reorganization is manifested by the drastic changes in the glycosidic angles (Δψ ≈ 100° and Δϕ ≈ 55° – the differences estimated for the starting and resulting (relaxed) structures for force f = 0.07 au).

IdoA^s-GlcN (dimer A). For the dimer A (with the starting ²S₀ conformer of IdoA) one can observe three distinct regions on the stretched/relaxed energy profile. The first region (denoted ① in Fig. 6(b)) corresponds to a simple stretching of the molecule (without any permanent structural changes). For forces in the range from 0.03 to 0.0325 au a slight energy shift can be observed. It corresponds to the conformational transition only in glucosamine unit (⁴C₁ → ²S₀), whereas iduronic acid conformer (²S₀) remains unaltered. The application of greater stretching force (see the region denoted ③ in Fig. 6(b)) involves a further increase in the dimer molecule length, associated with transitions in both saccharide units (IdoA^s and GlcN). Iduronic acid conformer ²S₀ flips to ⁴C₁ form, whereas glucosamine conformer ⁴C₁ transforms into ¹S₃ form. The total molecular elongation (11%) is considerably smaller than for IdoA^c-GlcN.

As before, the conformational changes in saccharide units are associated with the intramolecular structural rearrangement in the considered dimeric molecule. For example, the characteristic glycosidic dihedral angle Φ for the initial and resulting (stressed) structures vary form 14° to 34° for the maximum stretching force f = 0.07 au.

The relationship between the number of enforced conformational transitions and the sum of glycosidic and aglycone bonds in axial position has been suggested by Marszalek et al.²⁴ It also should be associated with the numbers of plateau on the force-extension curves. In this enforced process of the ring flipping, the equatorial substituents become axial, and the axial substituents become equatorial. As mentioned above, the staring ⁴C₁ conformer of GlcN has only one axially oriented (glycosidic) bond. Therefore, one would expect only one conformational transition in the glucosamine ring. Note that, in the case of dimer IdoA^c-GlcN and monomer GlcN, there is exactly one conformational flip ⁴C₁ → ¹S₃ in GlcN unit and the transition ⁴C₁ → ²S₀ does not take place. For dimeric IdoA^s-GlcN molecule in which GlcN unit is connected with the skew boat (²S₀) iduronic acid conformer, both structural changes occur. This finding is unexpected and suggests that the number of axially oriented bonds does not have to directly correlate with the number of conformational transitions, especially for more complicated structures as saccharide oligomers These changes may also depend on the different specific structural reasons (such as intermolecular hydrogen bonding, pyranose-ring substituents, position in oligomer/polymer structure etc.).

GlcA-GlcN (dimer B). In the case of GlcA-GlcN – dimer B there is only one plateau in the theoretical force-extension curve (Fig. 7) and one energy shift in the energy stretched (relaxed) profile (Fig. 6(c)). It corresponds to the conformational transition ⁴C₁ → ¹S₃ in the glucosamine unit. The glucuronic acid unit remains unchanged due to the equatorial positions of the terminal –OH groups. The maximum extension of the considered dimeric molecule is relatively small and it does not exceed 5%.

Pentameric structures

GlcN-IdoA^c-GlcN-GluA-GlcN. The results for the pentameric structure with the starting chair (¹C₄) conformer of iduronic acid (IdoA^c) are presented in Fig. 8(a) and 9. The external stretching force acting on oxygen atoms in the terminal –OH groups induces number of different structural changes in the considered molecule. It can be clearly seen from the stretched/relaxed energy profile (Fig. 8(a)). For forces f ≤ 0.0275 au the relaxation process of the stretched oligomer leads to its starting structure. In the next region (denoted as ②) one can observe the conformational transitions in the case of IdoA^c (¹C₄ → ⁰S₂) and one of terminal GlcN (⁴C₁ → ¹S₅) units.

Fig. 8 Energy of stretched (forced) and corresponding relaxed pentameric structures: (a) GlcN-IdoA^c-GlcN-GluA-GlcN, (b) GlcN-IdoA^s-GlcN-GluA-GlcN, as a function of applied external force.

Fig. 9 Theoretical force-extension curves (i.e. external stretching force vs. elongated molecule length) for pentameric structures.

The five remaining stages (③–⑦) in the stretching/relaxing profiles involves a rapid change in molecular length, associated with the mutual (different-type) transitions in three units, i.e. – both terminal GlcN units and iduronic acid monomer (for details see Fig. 8(a)). The enforced conformational-transition pathway for the iduronic acid unit in analyzed pentameric structure is consistent with the results obtained for monomeric IdoA^c and dimeric IdoA^c-GlcN structures, i.e. ¹C₄ → ⁰S₂ and ¹C₄ → ⁴C₁ for the suitable external forces. The similar situation takes place in the case of the terminal glucosamine unit connected with the iduronic acid monomer. Here, one can observe only one conformational transition ⁴C₁ → ¹S_3.

However, the starting structure (⁴C₁) of the second terminal glucosamine unit can transform into ¹S₃ or ¹S₅ conformer depending on the applied external force. The molecule lengths (defined as the distance between oxygen atoms involved in glycosidic bonds) of these skew-boat conformers in the relaxed pentameric structure do not vary much (difference does not exceed 0.015 Å).

As mentioned above, the enforced conformational transitions take place in the case of three saccharide units in the examined pentameric structure. The glucosamine (located in the center of the molecule) and glucuronic acid units are not permanently affected by the applied forces. In the relaxed pentameric structure these monomers retain their starting conformations (⁴C₁). While for GlcA unit it is not a surprising behavior (due to lack of the axial glycosidic linkages), for the glucosamine unit the conformational change(s) can be expected. However, it should be noted that the discussed (middle) glucosamine ring undergoes significant (temporary) deformations under external forces, but the relaxation after EGO process leads always to the starting conformer.

For maximum applied force (f = 0.075 au) the molecule elongates remarkably. The difference between molecular lengths of the initial and stretched structure equals nearly 10 Å (which constitutes more than 45% of initial molecular length). For forces greater than 0.075 au the glycosidic linkages between the saccharide units get broken.

GlcN-IdoA^s-GlcN-GluA-GlcN. The stretched/relaxed energy profile for pentameric structure GlcN-IdoA^s-GlcN-GluA-GlcN (with the starting skew-boat (²S₀) conformer of iduronic acid (IdoA^s)) presented in Fig. 8(b), can also be conveniently divided into several sections (①–⑥). The relaxed energies of the first two stages (① and ②) are very close. The energy shift is only about 0.002 au and it is not associated with any permanent conformational transitions. However, some structural changes take place and the difference in the molecular length of relaxed molecules of these stages equals 0.34 Å. In this case the spatial arrangements of the saccharide units are modified. The characteristic glycoside dihedral angles between IdoA^s and GlcN (located in the center of the molecule) units in relaxed structures vary considerably (ψ₁ = −168.6° and Φ₁ = −38.9° for f ≤ 0.020 au versus ψ₁ = −10.6°and Φ₁ = −19.4° for 0.0225 ≤ f ≤ 0.0275 au).

Additionally, one can observe the sudden trigger in the theoretical force-extension curve at f = 0.0225 au (see Fig 9). Let us note again, that this trigger does not correspond to the any conformational transition.

The next narrow step (denoted as ③ in Fig. 8(b)) is related to the conformational changes of two terminal glucosamine units, i.e., ⁴C₁ → ²S₀ and ⁴C₁ → ¹S₃ for GlcN-IdoA^s… and …GluA–GlcN oligomer ends, respectively. The remaining three internal saccharide units do not permanently change their conformations. Applying forces in the range of 0.0325–0.0350 au (region denoted as ④) causes the conformational transitions in both terminal GlcN units and additionally in the iduronic acid ring. In this case, both ⁴C₁ glucosamine units transform directly into ¹S₃ conformers, while the iduronic acid with the starting ²S₀ conformation adopts the ^2,5B form. Note, that the difference in the molecular length of these iduronic acid conformers (²S₀ and ^2,5B) does not exceed 0.01 Å. The two remaining stages (⑤ and ⑥) are associated with the different-type mutual transitions in all but one (i.e. GlcA) saccharide units (see Fig. 8(b)):

• ⁴C₁ → ¹S₃ for terminal GlcN unit connected with IdoA^s.

• ²S₀ → ⁴C₁ for iduronic acid dimer.

• ⁴C₁ → ¹S₅ for second terminal glucosamine units.

• two types of conformational changes in GlcN unit located in the center of the molecule, i.e. ⁴C₁ → ^2,5B for the external force 0.040 ≤ f ≤ 0.045 au (region denoted as ⑤) and ⁴C₁ → ¹S₃ for the forces from the range of 0.045–0.065 au (region denoted as ⑥).

For the highest applied stretching force (f = 0.065 au) the considered pentameric structure reaches its maximum molecular extension – i.e. about 30% increase in molecule length as compared to the initial structure.

Conclusions

In this work we focused on non-sulfated heparin-based oligosaccharides. The important feature of heparin polysaccharide is its high heterogeneity. We have considered three (neutral and non-sulfated) types of monosaccharide units (iduronic acid, glucosamine and glucuronic acid) and their appropriate dimeric and pentameric oligomers.

The major goal of this study was to examine possible conformational transitions induced in the glycopyranose rings by the external stretching forces applied to the two terminal glycosidic oxygen atoms of the considered molecules.

The courses of the enforced structural changes in polysaccharides may depend not only on the presence of the axially oriented terminal groups but also on different structural reasons. For example, the glucosamine unit (located in the center of the pentameric molecule GlcN-IdoA^c-GlcN-GluA-GlcN) is not permanently affected by the applied stretching force. In the relaxed structure this GlcN units retains its starting conformations (⁴C₁) although it has one axial glycosidic bond. Additionally, the conformational pathways for heparin residues in di- and pentameric oligosaccharides are not always consistent with the results obtained for the corresponding monomers. It was also shown that the position in (poly)/oligomeric structure may have significant effects on the nature and course of the force-driven conformational/structural changes. Moreover, in the presented theoretical force-extension curves not every plateau corresponds to a conformational transition and not every transition can be clearly seen. These results confirm that the proper interpretation of AFM data can be very difficult, especially for more complicated molecular systems.

Heparin glycosaminoglycan consists of a variably sulfated repeating saccharide unit (on average 1.8–2.6 sulfate groups per disaccharide). As mentioned above, the pyranose-ring substituents may determine the enforced structural changes. In this work we analyzed only non-sulfated molecules and therefore the sulfation effect has not been taken into account. Note that, the investigated unique pentameric structure of heparin is responsible for binding to antithrombin III (ATIII) and enhancing the inhibitory effect of this protein on a number of procoagulant proteases. The high binding affinity may depend on the orientation of carboxylate and sulphate substituents in heparin oligomers.¹³ The enforced structural changes probably will be associated with the significant spatial arrangement of these functional groups and it may have an effect on strength of binding to ATIII protein.

Moreover, we considered only neutral, non-ionic heparin-based oligosaccharides. At physiological pH O-sulfated, N-sulfated and carboxylic groups are ionized and heparin exists as a polyanion.⁴⁰ It should be noted that the equilibrium structure of the heparin anionic form(s) may change considerably in a water solution.^1,2,41,42 These changes in geometry of pyranose rings and glycosidic linkage conformation may depend on solvation and electrostatic solvent effects and also the type of the counterion.^6,41 Hydration may also cause conformational rearrangement of the functional groups and change the intramolecular hydrogen bonds.

The association of mentioned above factors (sulfation, ionization status of the molecule, presence of the solvent) and their effects on force-driven conformational properties in heparin will be investigated in future studies.

Notes and references

1. M. Remko and C.-W. von der Lieth, J. Chem. Inf. Model., 2006, 46, 1687–1694.
2. M. Remko and C.-W. von der Lieth, J. Phys. Chem. A, 2007, 111, 13484–13491.
3. M. Remko, P. Duijnen and R. Broer, Struct. Chem., 2010, 21, 965–976.
4. C. Guo, B. Wang, L. Wang and B. Xu, Chem. Commun., 2012, 48, 12222.
5. M. Remko, P. T. V. Duijnen and R. Broer, RSC Adv., 2013, 3, 1789.
6. M. Remko, P. T. Van Duijnen and R. Broer, RSC Adv., 2013, 3, 9843.
7. L. Jin, M. Hricovini, J. A. Deakin, M. Lyon and D. Uhrin, Glycobiology, 2009, 19, 1185–1196.
8. J. C. Munoz-Garcia, F. Corzana, J. L. de Paz, J. Angulo and P. M. Nieto, Glycobiology, 2013, 23, 1220–1229.
9. S. A. Samsonov and M. T. Pisabarro, Carbohydr. Res., 2013, 381, 133–137.
10. T. F. Gesteira, L. Pol-Fachin, V. J. Coulson-Thomas, M. A. Lima, H. Verli and H. B. Nader, PLoS One, 2013, 8, e70880.
11. H. Verli and J. A. Guimarães, Carbohydr. Res., 2004, 339, 281–290.
12. B. Mulloy and M. J. Forster, Glycobiology, 2000, 10, 1147–1156.
13. P. E. Marszalek, A. F. Oberhauser, H. Li and J. M. Fernandez, Biophys. J., 2003, 85, 2696–2704.
14. B.-M. Loo, J. Biol. Chem., 2002, 277, 32616–32623.
15. A. Canales, J. Angulo, R. Ojeda, M. Bruix, R. Fayos, R. Lozano, G. Giménez-Gallego, M. Martín-Lomas, P. M. Nieto and J. Jiménez-Barbero, J. Am. Chem. Soc., 2005, 127, 5778–5779.
16. A. Kern, K. Schmidt, C. Leder, O. J. Muller, C. E. Wobus, K. Bettinger, C. W. Von der Lieth, J. A. King and J. A. Kleinschmidt, J. Virol., 2003, 77, 11072–11081.
17. Y. Seo, A. Andaya and J. A. Leary, Anal. Chem., 2012, 84, 2416–2423.
18. V. S. R. Rao, Conformation of carbohydrates, Harwood, Amsterdam, 1998.
19. G. Pavlov, S. Finet, K. Tatarenko, E. Korneeva and C. Ebel, Eur. Biophys. J., 2003, 32, 437–449.
20. B. Casu and U. Lindahl, in Advances in Carbohydrate Chemistry and Biochemistry, Academic Press, 2001, vol. 57, pp. 159–206.
21. H. Li, M. Rief, F. Oesterhelt, H. E. Gaub, X. Zhang and J. Shen, Chem. Phys. Lett., 1999, 305, 197–201.
22. M. Hricovíni, M. Guerrini, A. Bisio, G. Torri, M. Petitou and B. Casu, Biochem. J., 2001, 359, 265–272.
23. G. Torri, B. Casu, G. Gatti, M. Petitou, J. Choay, J. C. Jacquinet and P. Sinaÿ, Biochem. Biophys. Res. Commun., 1985, 128, 134–140.
24. P. Marszalek, A. Oberhauser, Y. Pang and J. Fernandez, Nature, 1998, 396, 661–664.
25. K. Wolinski and J. Baker, Mol. Phys., 2009, 107, 2403–2417.
26. K. Wolinski and J. Baker, Mol. Phys., 2010, 108, 1845–1856.
27. J. Baker and K. Wolinski, J. Mol. Model., 2010, 17, 1335–1342.
28. J. Baker and K. Wolinski, J. Comput. Chem., 2011, 32, 43–53.
29. D. Kosztin, S. Izrailev and K. Schulten, Biophys. J., 1999, 76, 188–197.
30. S. Park and K. Schulten, J. Chem. Phys., 2004, 120, 5946.
31. B. M. Sattelle, S. U. Hansen, J. Gardiner and A. Almond, J. Am. Chem. Soc., 2010, 132, 13132–13134.
32. A. Bérces, D. M. Whitfield and T. Nukada, Tetrahedron, 2001, 57, 477–491.
33. G. Gatti, B. Casu, G. K. Hamer and A. S. Perlin, Macromolecules, 1979, 12, 1001–1007.
34. E. D. Atkins and I. A. Nieduszynski, Adv. Exp. Med. Biol., 1975, 52, 19–37.
35. I. A. Nieduszynski, K. H. Gardner and E. D. T. Atkins, in Cellulose Chemistry and Technology, American Chemical Society, 1977, vol. 48, pp. 73–90.
36. B. Mulloy, M. J. Forster, C. Jones and D. B. Davies, Biochem. J., 1993, 293(3), 849–858.
37. J. Baker, K. Wolinski, T. Janowski, S. Saeboand P. Pulay, PQS version 4.0, Parallel Quantum Solutions, Parallel Quantum Solutions P.O. Box 293 Fayetteville Arkansas 72702-0293 USA.
38. N. S. Gandhi and R. L. Mancera, Carbohydr. Res., 2010, 345, 689–695.
39. S. Ernst, G. Venkataraman, V. Sasisekharan, R. Langer, C. L. Cooney and R. Sasisekharan, J. Am. Chem. Soc., 1998, 120, 2099–2107.
40. M. Remko, R. Broer and P. T. Van Duijnen, Chem. Phys. Lett., 2013, 590, 187–191.
41. M. Hricovíni, J. Phys. Chem. B, 2011, 115, 1503–1511.
42. M. Remko, M. Swart and F. M. Bickelhaupt, J. Phys. Chem. B, 2007, 111, 2313–2321.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed numerical results are attached (ESI.pdf). The EGO simulation for considered pentameric structures – please check out the mp4 files. See DOI: 10.1039/c4ra05530f

---