Residence time distribution analysis and kinetic study of toluene photo-degradation using a continuous immobilized photoreactor
Morteza Jafarikojoura,
Morteza Sohrabi*ab,
Sayed Javid Royaeec and
Mohammad Rezaeia
aChemical Engineering Department, Amirkabir University of Technology, Tehran, Iran
bIran Academy of Sciences, Tehran, Iran. E-mail: Sohrabi@aut.ac.ir
cPetroleum Refining Technology Development Division, Research Institute of Petroleum Industry, Tehran, Iran
First published on 8th October 2014
Abstract
The photocatalytic degradation of volatile organic compounds is an innovative intensification technology. In this study, photocatalytic degradation of toluene has been investigated in a novel continuous immobilized photoreactor and the flow regimes were characterized and modeled by means of residence time distribution (RTD) of the gas phase. RTD analysis indicates that the flow regime in such a reactor cannot be considered as perfect plug and that a significant axial dispersion is available. A compartment model consisting of fourteen continuous stirred tank reactors was assigned to describe the flow pattern in the reactor. A Langmuir–Hinshelwood (L–H) kinetics scheme has been used to describe the degradation of toluene to model the behavior of the reaction system. A number of different assumptions were made, i.e. the perfect plug flow model, the plug-flow with axial dispersion model and the continuous stirred tank reactors in series model. A comparison was made between the sum of the square errors (SSE) for experimental and predicted degradation ratios for each flow model revealing that continuous stirred tank reactors in series were a better description for the photocatalytic degradation of toluene.
1. Introduction
Volatile organic compounds (VOCs) that are widely used in chemical, agricultural and food processing industries are well known to be malodorous and toxic.1 Toluene is one of the typical VOCs that threaten human health. As toluene is toxic, carcinogenic and environmentally persistent, it has been classified as a priority hazardous substance.2 Among all advanced technologies for fast and economical degradation of VOCs from indoor air, photocatalytic processes using a semi-conductor as a photocatalyst has received growing interests in the subsequent three decades.3–6 UV light irradiation emitting photons with sufficient energy, i.e. equal or higher than the band-gap energy of the catalyst, forms some high reactive electron–hole pairs in TiO2 that decompose VOCs by redox reactions.3,6Regarding from both economical and practical aspects, reactors that utilize TiO2 catalyst as immobilized films have a significant advantage over those utilizing suspended TiO2 powder.7–9
There are several laboratory-scale immobilized photoreactors reported in literature such as honeycomb,10 annular,11,12 packed bed13 and plate14 developed for air treatment using UV/TiO2 combination. In general, an efficient photoreactor should have a high specific surface area, small pass-through channels and low air velocity for a high mass transfer and direct light irradiation to the reaction area.4 Owing to the fact that almost every photoreactors have some disadvantages, it is necessary to design and develop a new photoreactor in order to achieve high performance for degrading VOCs. There is a consensus that design and modeling of photocatalytic reactors is a promising new area for research.15–17 Photocatalytic reactors are often different from ideal reactors (batch, perfect mixed and plug flow reactors).18 Hence, determination of the residence time distribution (RTD) for the flow regimes in the reactor is a key information required for successful design, modeling and scale-up of the latter devices.19,20 On the basis of RTD data, it may be possible to simulate non-ideal systems by a configuration of ideal systems, including ideal perfect mixed and/or ideal plug flow reactors.18,21 Reactor modelling is sometimes based on two simple flow models (axial dispersion model and continuous stirred tank reactors in series).19 Langmuir–Hinshelwood kinetic model is generally applied to describe the photocatalytic degradation of toluene.22–24 Evaluating reactor performance under conditions that mass and photon transfer limitations are not predominant is an important requirement for the determination of the intrinsic kinetic coefficients independent from the reactor configuration.8,25
In this study, a new designed immobilized photocatalytic reactor is modelled and the capability of which to degrade toluene in the gas phase was assessed. A simple structure and avoiding catalyst separation difficulties by coating the photocatalyst on fixed supports may be regarded as advantages that could make this photoreactor industrially feasible. The flow regime in the photoreactor need to be characterized in order to obtain a comprehensive insight to the latter, better control of the process and determination of the intrinsic kinetic coefficients independent from the reactor configuration. At the first step, residence time distribution (RTD) was initially determined to characterize the immobilized photoreactor hydraulic behaviour. The reactor was then modelled, applying both a cascade of continuous stirred tank reactors (CSTRs) and the axial dispersion models. The results of these models were used to predict the rate coefficients for degradation reaction. The main novelty of this work relates to the model development, which considers both hydraulics and mass transfer in the reactor with the chemical kinetics. The results predicted by the model were compared with experimental results for various toluene concentrations and gas flow rates. Once the intrinsic kinetics coefficients and model of the reactor are known, they can be used in different reactor configurations. This model can form a major element in designing and scaling-up the immobilized photoreactors.
2. Experimental
2.1. Materials
Aeroxide® P25-TiO2 Powder (Evonik; BET surface area of 53.9 m2 g−1, pore volume of 0.172 m3 g−1, 70% anatase/30% rutile) was purchased from Evonik (Germany). In addition, ethanol (C2H5OH, Mr = 46.07) and nitric acid (HNO3, 65%) were both obtained from Merck Co. (Germany).2.2. Photoreactor and photocatalytic degradation conditions
Fig. 1a displays the schematic diagram and dimensions of the illuminated photocatalytic immobilized reactor. The photoreactor consisted of two coaxial cylinders. The outer cylinder was made of pyrex glass (70 mm inside diameter and 330 mm in length) while the inner cylinder was made of quartz (25 mm outside diameter and 330 mm in length). A UV light source (15W-ZW15D15W-Z303, China), with peak intensity at 254 nm, 15 mm in diameter and 240 mm in length was located at the center of the quartz cylinder. Two types of perforated stainless steel (304) disks, coated with TiO2 nanoparticles were installed inside the reactor in a certain configuration. The disks were placed alternately within the reactor in a way that small disks were attached to the inner cylinder and the larger ones were attached to the outer cylinder (Fig. 1a). The 28 discs were so arranged to form a zigzag pattern for the gas flow along the reactor length. Fig. 1b indicates the illuminated photoreactor. Although, the UV light in this reactor is parallel to the reaction area, it has a large specific surface area (0.1460 m2) coated with TiO2 photocatalyst in a small volume (665 ml). besides, Baffles to make narrow paths for air crossing are an efficient and cheap method to create a proper mixing flow inside the reactor and as a result provide high mass transfer inside the reactor. These properties suggest that this reactor could have a good performance for the degradation of toluene. | ||
| Fig. 1 (a) Arrangement and dimensions of the photoreactor (not to scale) (b) experimental scale illuminated photoreactor. | ||
The prepared photocatalyst was deposited on the stainless steel supports. First, 15 g of TiO2 powder was added to 300 ml ethanol with vigorous stirring to form a slurry. Forty five ml of dilute nitric acid with pH 3.5 was then added to the slurry. The slurry was stirred at room temperature for approximately 2 h and then sonicated for 30 min in order to make the slurry further uniform. The uncoated stainless steel discs were cleaned with both ethanol and distilled water and were dried under atmospheric conditions. Stainless steel disks were dipped into the slurry by an in-house developed, electrically driven pulley system. The disks were dipped into slurry at a rate of 22 cm min−1 and then were held in slurry for 5 min. Withdrawal speed was also 22 cm min−1. In the next step, the coated disks were dried at room temperature for 12 h and then placed into a furnace. The furnace temperature was elevated to 350 °C at a ramp rate of 15 °C min−1 and then maintained at the latter temperature for 30 min.
As shown in Fig. 2, the experimental set-up consists of air and vapor feed delivery system, the photoreactor and an analytical unit. The toluene vapor feed rate was controlled using a syringe pump (SK-5001-China). The vaporized toluene was mixed with dry or wet air in a mixing chamber before entering to the photoreactor. The air flow was divided into two separate streams. One of the air streams was saturated by bubbling in distillated water. The outlet stream from the saturating chamber was then mixed with the unsaturated second stream and entered the reactor. Temperature and relative humidity were monitored continuously, using a digital thermo-hygrometer (TFA-Germany). The reactor inlet and outlet gas mixtures were analyzed by a GC-FID (GC-14B, Shimazu Co., Japan-PH5, applying a capillary column (0.32 mm i.d. × 30 m)). The column oven temperature was held at 60 °C for 15 min. The temperature of the injector port was set at 280 °C. A split injection mode was used (ratio = 3.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). The carrier gas (helium) flow rate was 1.8 ml min−1. The experimental set-up generates polluted air with various inlet concentrations and gas flow rates so that kinetic study could be performed.
1). The carrier gas (helium) flow rate was 1.8 ml min−1. The experimental set-up generates polluted air with various inlet concentrations and gas flow rates so that kinetic study could be performed.
2.3. Experimental conditions of RTD study
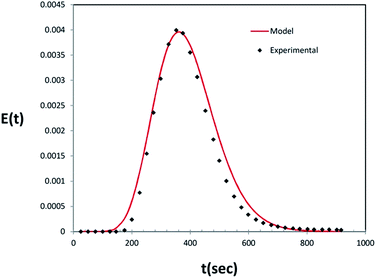
To characterize the gas flow pattern in the photoreactor, the gas residence time distribution was determined at a flow rate of 100 ml min−1. To simulate a pulse function (Dirac delta function), a tracer (CO2) was injected in at time t = 0 s to the inlet stream of the reactor within a very short time, using a micro syringe. Carbon dioxide concentration was measured and plotted versus time using a Testo-445 device (provided by Testo Inc.; Germany) placed at the outlet of the photoreactor (Fig. 3).3. Photocatalytic results and discussion
3.1. Photoreactor modeling
The residence time distribution (RTD) of a chemical reactor is defined as the distribution function that determine average time that gas molecules spend inside the reactor.26 Fraction of material in the outlet stream that has been in the reactor during the period between t and t + dt, is equal to E(t)dt. Where E(t) is called the exit age distribution function of the fluid elements leaving the reactor and is expressed as a function of time by the following equation:27,28
 | (1) |
The RTD experiment was performed by measuring the concentration of tracer at intervals of 25 seconds using a flow rate of 100 ml min−1. The RTD curve was plotted applying eqn (1) (Fig. 4). To characterize the non-ideal flow within reactors, a number of models have been developed. However, there are two common models for description of the residence time pattern and dispersion in a reactor; namely, continuous stirred tank reactors in series and dispersion models.19 Since RTD curve is only known at a number of discrete time values, the mean gas residence time (![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) m), the variance of the residence time (σ2) and the dimensionless variance (σθ2) are expressed by:18
m), the variance of the residence time (σ2) and the dimensionless variance (σθ2) are expressed by:18
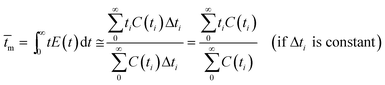 | (2) |
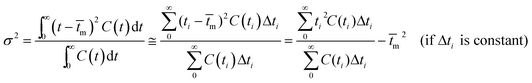 | (3) |
 | (4) |
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) m) of 389 s and dimensionless variance (σθ2) of 0.069 were calculated at gas flow rate of 100 ml min−1. As the vessel dispersion number is not low (D/uL > 0.01) the degree of axial dispersion may not be neglected. This is confirmed by the RTD curve where the pulse response is broad and not completely symmetrical with a short tail representing a flow pattern between plug flow and completely mixed regimes (Fig. 4). In such a case, for closed–closed boundary conditions assuming that the inlet and outlet streams are both perfect plug flow, the modified dimensionless variance was first given by van der Laan:29
m) of 389 s and dimensionless variance (σθ2) of 0.069 were calculated at gas flow rate of 100 ml min−1. As the vessel dispersion number is not low (D/uL > 0.01) the degree of axial dispersion may not be neglected. This is confirmed by the RTD curve where the pulse response is broad and not completely symmetrical with a short tail representing a flow pattern between plug flow and completely mixed regimes (Fig. 4). In such a case, for closed–closed boundary conditions assuming that the inlet and outlet streams are both perfect plug flow, the modified dimensionless variance was first given by van der Laan:29
 | (5) |
From eqn (5) dimensionless variance (σθ2) and D/uL of 0.067 and 0.0335 were calculated, respectively.
In continuous stirred tank reactors in series model, the actual volume of the photoreactor can be replaced by N equal sized ideal stirred tank reactors (Fig. 5a). The number of tanks may be calculated from eqn (6).
 | (6) |
It is generally accepted that above 20 mixed reactors in series, the flow may be regarded as perfect plug. In such a case the RTD curve becomes approximately Gaussian.1 The number of CSTR (N) representing the flow within the photoreactor was 14.39 for flow rates of 100 ml min−1. The expression for the theoretical RTD of this model can be predicted using Martin Method which uses a Gamma distribution:30
 | (7) |
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) m is the mean residence time and N is total number of continuous stirred tank reactors. The expected E(t) curve from the tanks-in-series model for a cascade of fourteen continuous stirred tank reactors (N = 14) was plotted in Fig. 4. If the N number was considered 14, it can be assumed that each two baffles in the proposed photoreactor work like a CSTR (Fig. 5b).
m is the mean residence time and N is total number of continuous stirred tank reactors. The expected E(t) curve from the tanks-in-series model for a cascade of fourteen continuous stirred tank reactors (N = 14) was plotted in Fig. 4. If the N number was considered 14, it can be assumed that each two baffles in the proposed photoreactor work like a CSTR (Fig. 5b).
3.2. Degradation kinetic model
| C7H8 + 9O2 → 4H2O + 7CO2 | (8) |
The effect of initial toluene concentration on the photocatalytic degradation rate was investigated in the range of 0.0811–0.406 mg l−1 when the gas flow rate and relative humidity were 100 ml min−1 and 30%, respectively.
There are intensive reports showing that the photocatalytic destruction of VOCs on TiO2 surfaces is assumed to follow single-site Langmuir–Hinshelwood kinetics (L–H).23,31–33 This model successfully explains the kinetics of reactions that occur between two adsorbed species (a free radical (i.e. OH˙) and an adsorbed substrate, or a surface-bound radical and a free substrate).24 A system having over 20 ideal CSTRs in series may be considered to behave as the plug flow reactor. However, as the first approximation the photoreactor was assumed to be a perfect plug flow apparatus. At constant oxygen and water vapor concentrations, and considering that the adsorption of reaction intermediates and products on the catalyst is not rate determining step, the L–H model describing toluene degradation kinetics in a plug flow reactor can be given by eqn (9).1
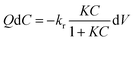 | (9) |
Integrating eqn (9) between the reactor's inlet and outlet concentrations yield:
 | (10) |
To determine the kinetic coefficients, an optimization program was applied by which the sum of the square errors (SSE) for experimental and predicted degradation ratios is minimized:
 | (11) |
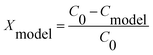 | (12) |
 | (13) |
The linear plot of (V/QCinX) against ln(1 − X)/CinX presented in Fig. 6 demonstrates that the Langmuir Hinshelwood model may be appropriate representation for the photocatalytic degradation of toluene. From the linear, the values for kr and K were determined as 0.0621 mg min−1 l−1 and 2.462 l mg−1, respectively.
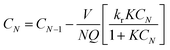 | (14) |
(i) The proposed reactor is equivalent to a tubular reactor with a vessel dispersion number of 0.0335 (Fig. 7).
(ii) The fluid is flowing with a uniform velocity through the reactor and is being mixed axially with an axial dispersion coefficient of D.
(iii) Axial dispersion coefficient is independent of concentration.
(iv) Radial dispersion coefficient is negligible in comparison with axial dispersion.
(v) Steady state conditions are prevailed.
A material balance around differential element (dz) in the reactor leads to the following equation:29
 | (15) |
By replacing the L–H kinetics model in eqn (17);
 | (16) |
Eqn (18) has been solved by a numerical method, using the Newton–Raphson method applying the following closed–closed boundary conditions:29
 | (17) |
 | (18) |
To determine the kinetic coefficients, an optimization toolbox has been used by which the value of SSE was minimized. From such an optimization, the values for kr, K and SSE were determined as 0.3569 mg min−1 l−1, 3.854 l mg−1 and 0.00038, respectively.
The effect of the toluene inlet concentration on toluene degradation ratio (X) and fitting of the models is illustrated in Fig. 8. The kinetic constants, experimental and predicted degradation ratios and SSEs of each model are presented in Table 1.
| Experimental | Continuous stirred tank reactors in series | Plug-flow with axial dispersion model | |
|---|---|---|---|
| C0 (mg l−1) | Xexperimental | Xmodel | Xmodel |
| 0.0811 | 0.59 | 0.60 | 0.60 |
| 0.162 | 0.56 | 0.57 | 0.55 |
| 0.243 | 0.53 | 0.52 | 0.51 |
| 0.325 | 0.47 | 0.48 | 0.47 |
| 0.406 | 0.41 | 0.45 | 0.43 |
| kr (mg min−1 l−1) | 0.2361 | 0.3569 | |
| K (l mg−1) | 3.235 | 3.854 | |
| SSE | 0.00021 | 0.00038 | |
As it can be observed from Table 1 and Fig. 8, SSEs for experimental and predicted values in case of each model approach revealed that there is a good agreement between both models (continuous stirred tank reactors in series and dispersion models) and experimental results. However, CSTRs in series model seems to be more consistent with the experimental data. This may be due to the higher vessel dispersion number observed in the present study (D/uL = 0.0335). The suitable magnitude of such a number for better correlation of experimental results with dispersed plug flow model is 0.001–0.01.29 In order to study the influence of mass transfer limitation on the process, the experimental degradation ratios results from immobilized reactor were compared with those of perfect plug-flow model (eqn (10)). Although plug flow model is fairly well correlated with the photocatalytic degradation of toluene (Fig. 6), it may not be a justified assumption. As it can be seen from Fig. 9, the experimental results determined for three different flow rates and initial concentrations of toluene do not fall on a single line indicating that the flow regime in photoreactor may not be described by the perfect plug-flow.8 In addition, the nonsymmetrical RTD (section 3.1) indicates that such an assumption may not be justified and that the kinetic parameters determined using such an assumption are not independent from the reactor configuration and mass transfer limitations.
4. Conclusions
Photocatalytic decomposition of toluene in gas phase was investigated in an immobilized photoreactor with toluene inlet concentrations range of 0.0811 to 0.406 mg l−1, gas flow rate between 100 and 500 ml min−1 and relative humidity of 30%, using Evonik P25 as a photocatalyst. Data for the RTD of fluid in the exit stream of the photoreactor were obtained using the impulse tracer method. Gas residence time distribution curves revealed that both the axial dispersion model for the photoreactor flow regime with vessel dispersion number of 0.0335 and tanks-in-series model with a cascade of fourteen ideal CSTR were well correlated with the reactor behavior. It is also evident from the results that continuous stirred tank reactors in series is a better description for the degradation results in comparison with perfect plug flow and dispersed plug flow models.Nomenclature
| E | Residence time distribution |
![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) m m | Mean gas residence time (min) |
| σ2 | Variance of the residence time |
| σ2θ | Dimensionless variance |
| D | Axial dispersion coefficient (m2 s−1) |
| U | Flow velocity (m s−1) |
| L | Characteristic length of the reactor (m) |
| D/uL | Vessel dispersion number |
| N | Number of equal sized ideal stirred tank reactors |
| K | Adsorption equilibrium constant (l mg−1) |
| C | Toluene concentration (mg l−1) |
| C0 | Reactor inlet toluene concentration (mg l−1) |
| kr | Apparent reaction rate coefficient (mg min−1 l−1) |
| Q | Volumetric flow rate (l min−1) |
| V | Photoreactor volume (m3) |
| SSE | Sum of the square errors |
| nexp. | Total number of experiments |
| Xexp. | Experimental degradation ratio |
| Xmodel | Model degradation ratio |
| CN−1 | Inlet toluene concentrations from the Nth reactor |
| CN | Outlet toluene concentrations from the Nth reactor |
Acknowledgements
The authors would like to thank Evonik GmbH for kindly supplying Nano-sized TiO2.References
- G. Vincent, P. M. Marquaire and O. Zahraa, J. Hazard. Mater., 2009, 161, 1173–1181 CrossRef CAS PubMed.
- X. Li, X. Zou, Z. Qu, Q. Zhao and L. Wang, Chemosphere, 2011, 83, 674–679 CrossRef CAS PubMed.
- H. Einaga, S. Futamura and T. Ibusuki, Environ. Sci. Technol., 2001, 35, 1880–1884 CrossRef CAS PubMed.
- J. Mo, Y. Zhang, Q. Xu, J. J. Lamson and R. Zhao, Atmos. Environ., 2009, 43, 2229–2246 CrossRef CAS.
- C. F. Daniel Vildozo, M. Sleiman and J.-M. Chovelon, Appl. Catal., B, 2010, 94, 303–310 CrossRef.
- G. Vincent, E. Schaer, P.-M. Marquaire and O. Zahraa, Process Saf. Environ. Prot., 2011, 89, 35–40 CrossRef CAS.
- Y. Chen and D. D. Dionysiou, Appl. Catal., B, 2006, 62, 255–264 CrossRef CAS.
- G. Charles, T. Roques-Carmes, N. Becheikh, L. Falk, J.-M. Commenge and S. Corbel, J. Photochem. Photobiol., A, 2011, 223, 202–211 CrossRef CAS.
- S. M. B. S. N. Hosseini, M. Vossoughi and N. Taghavinia, Appl. Catal., B, 2007, 74, 53–62 CrossRef CAS.
- M. M. Hossain, G. B. Raupp, S. O. Hay and T. N. Obee, AIChE J., 1999, 45, 1309–1321 CrossRef CAS.
- J. Mo, Y. Zhang, R. Yang and Q. Xu, Build. Environ., 2008, 43, 238–245 CrossRef.
- G. Vincent, P. M. Marquaire and O. Zahraa, J. Photochem. Photobiol., A, 2008, 197, 177–189 CrossRef CAS.
- M. Mehrvar, W. A. Anderson and M. Moo-Young, Adv. Environ. Res., 2002, 6, 411–418 CrossRef CAS.
- I. Salvadó-Estivill, A. Brucato and G. Li Puma, Ind. Eng. Chem. Res., 2007, 46, 7489–7496 CrossRef.
- G. Li Puma and P. L. Yue, Chem. Eng. Sci., 2003, 58, 2269–2281 CrossRef CAS.
- J. Marugán, R. van Grieken, C. Pablos, M. L. Satuf, A. E. Cassano and O. M. Alfano, Chem. Eng. J., 2013, 224, 39–45 CrossRef.
- G. E. Imoberdorf, A. E. Cassano, H. A. Irazoqui and O. M. Alfano, Catal. Today, 2007, 129, 118–126 CrossRef CAS.
- M. Fathinia and A. R. Khataee, J. Ind. Eng. Chem., 2013, 19, 1525–1534 CrossRef CAS.
- W. Wibel, A. Wenka, J. J. Brandner and R. Dittmeyer, Chem. Eng. J., 2013, 227, 203–214 CrossRef CAS.
- S. S. Waje, A. K. Patel, B. N. Thorat and A. S. Mujumdar, Drying Technol., 2007, 25, 249–259 CrossRef.
- S. J. Royaee and M. Sohrabi, Ind. Eng. Chem. Res., 2012, 51, 4152–4160 CrossRef CAS.
- Z. Wei, J. Sun, Z. Xie, M. Liang and S. Chen, J. Hazard. Mater., 2010, 177, 814–821 CrossRef CAS PubMed.
- A. Bouzaza and A. Laplanche, J. Photochem. Photobiol., A, 2002, 150, 207–212 CrossRef CAS.
- V. Augugliaro and R. S. o. Chemistry, Clean by Light Irradiation: Practical Applications of Supported TiO2, Royal Society of Chemistry, 2010 Search PubMed.
- S. Royaee, M. Sohrabi and M. Jafarikojour, Res. Chem. Intermed., 2014, 1–23, DOI:10.1007/s11164-014-1750-2.
- E. Sahle-Demessie, S. Bekele and U. R. Pillai, Catal. Today, 2003, 88, 61–72 CrossRef CAS.
- G. Vincent, A. Queffeulou, P. M. Marquaire and O. Zahraa, J. Photochem. Photobiol., A, 2007, 191, 42–50 CrossRef CAS.
- V. Sans, N. Karbass, M. I. Burguete, E. Garcia-Verdugo and S. V. Luis, RSC Adv., 2012, 2, 8721–8728 RSC.
- O. Levenspiel, Chemical Reaction Engineering, John Wiley & Sons, New York, 1999 Search PubMed.
- Y. Wang, S. Liu, M. Brannock and G. Leslie, Desalination, 2009, 236, 120–126 CrossRef CAS.
- J. Palau, M. Colomer, J. M. Penya-Roja and V. Martínez-Soria, Ind. Eng. Chem. Res., 2012, 51, 5986–5994 CrossRef CAS.
- C. A. Korologos, M. D. Nikolaki, C. N. Zerva, C. J. Philippopoulos and S. G. Poulopoulos, J. Photochem. Photobiol., A, 2012, 244, 24–31 CrossRef CAS.
- F. Moulis and J. Krýsa, Catal. Today, 2013, 209, 153–158 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |