Influence of different membrane environments on the behavior of cholesterol†
Abstract
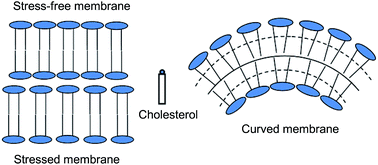
With the aid of molecular dynamics simulations, we study the behavior of cholesterol in several representative membrane environments. Especially, we pay attention to the relation between local lipid packing and the thermodynamic properties of cholesterols in different membranes. It is found that the entropy and enthalpy values of cholesterols in different membranes depend on the membrane lipid packing. Loose lipid packing always corresponds to favorable entropy but disadvantaged enthalpy, while dense lipid packing has an opposite role. We further investigate the transbilayer distribution of cholesterols in curved membrane and find that the cholesterol will adjust its distribution in the two leaflets of curved membrane as the two leaflets have different lipid packing styles. And quantitatively, we present a simple theory model to explain the redistribution of cholesterols in curved membrane and discuss its potential impact on the membrane deformation process.

 Please wait while we load your content...
Please wait while we load your content...