Defect induced magnetism in planar silicene: a first principles study
Abstract
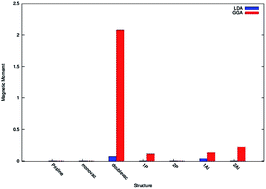
We study here the magnetic properties of two dimensional silicene using spin polarized density functional theory. The magnetic properties were studied by introducing monovacancy and di-vacancy, as well as by doping phosphorous and aluminium into the pristine silicene. It is observed that there is no magnetism in the monovacancy system, while there is large significant magnetic moment present for the di-vacancy system. Besides, the numerical computation reveals that the magnitude of the magnetic moment is more when the system is doped with aluminium than phosphorous. All these theoretical predictions in this two dimensional system may shed light to open a new route to design silicon based nano-structures in spintronics.

 Please wait while we load your content...
Please wait while we load your content...