Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Natural rubber for sustainable high-power electrical energy generation†
Rainer
Kaltseis
*ab,
Christoph
Keplinger
abc,
Soo Jin
Adrian Koh
de,
Richard
Baumgartner
a,
Yu Feng
Goh
e,
Wee Hoe
Ng
e,
Alexander
Kogler
a,
Andreas
Tröls
a,
Choon Chiang
Foo
bd,
Zhigang
Suo
b and
Siegfried
Bauer
a
aDepartment of Soft Matter Physics, Johannes Kepler University, Linz, A-4040, Austria. E-mail: rainer.kaltseis@gmail.com
bSchool of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138, USA
cKavli Institute for Bionano Science and Technology, Harvard University, Cambridge, Massachusetts 02138, USA
dInstitute of High Performance Computing, 1 Fusionopolis Way, #16-16 Connexis, Singapore 138632, Singapore
eDepartment of Mechanical Engineering and Engineering Science Programme, National University of Singapore, 9 Engineering Drive 1, Kent Ridge, Singapore 117576, Singapore
First published on 16th June 2014
Abstract
Clean, renewable and abundant sources of energy, such as the vast energy of ocean waves, are untapped today, because no technology exists to convert such mechanical motions to electricity economically. Other sources of mechanical energy, such as motions of people and vibrations of buildings and bridges, can potentially power portable electronics and distributed sensors. Here we show that natural rubber can be used to construct generators of high performance and low cost. Natural rubber has higher elastic modulus, fracture energy and dielectric strength than a commonly studied acrylic elastomer. We demonstrate high energy densities (369 mJ g−1) and high power densities (200 mW g−1), and estimate low levelized cost of electricity (5–11 ct kW−1 h−1). Soft generators based on natural rubber enable clean, low-cost, large-scale generation of electricity.
Introduction
Hydropower and winds have been harvested economically, but most other sources of mechanical energy, such as human motions, ocean waves, and building vibrations, have remained untapped. Harvesting these sources of energy is highly desirable. On a small scale, for example, the power generated from the heels of a walking person may charge mobile devices; a full charge of a smart phone requires about 0.1% of our daily energy uptake. On a large scale, ocean waves contain sufficient energy to satisfy the total worldwide demand for electrical energy.1No technologies, however, exist to convert these sources of mechanical energy to electricity at low cost. For example, many designs have been proposed to harvest ocean wave energy,2 but they are not economically competitive. These devices couple with the ocean waves through large and repeated motions of hard materials. They are costly to construct and maintain in the harsh ocean environment.3 Here we show that natural rubber can be used to convert mechanical motions to electricity at high energy and power density, at potentially low cost.
Natural rubber is inexpensive and robust, and has been used in oceans for well over a century as electrical insulators, buoys, etc.4,5
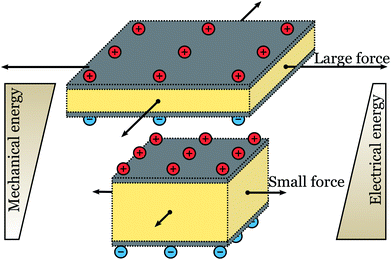
A soft generator involves a deformable capacitor operating through electromechanical cycles.6–12 A membrane of a soft dielectric is sandwiched between two compliant conductors. The two conductors carry electric charges of the opposite polarities (Fig. 1). In one state, a mechanical force stretches the membrane, and the voltage between the two conductors is low. In the other state, when the mechanical force reduces, the membrane decreases the area and increases the thickness, raising the fixed amount of charges to a higher voltage. The change between the two states enables the mechanical force to raise the fixed amount of electrical charges to higher voltage.
Existing demonstrations of soft generators have used acrylic6,8,13–15 and silicone-based10,16 elastomers. The relatively high cost of these elastomers have prevented them from large-scale applications.17–19 In addition, the acrylic elastomers are highly viscous; the large energy loss limits the frequency range and conversion efficiency. Furthermore acrylic elastomers have relatively low fracture energy often leading to rupture under electromechanical loads.20 We show that natural rubber is much less viscous, and has higher fracture toughness and dielectric strength than the acrylic elastomers. This work asses the aptitude of three materials employed in the same experimental setup, to provide comparative results. We demonstrate the energy conversion capability of natural rubber, and use the results to illustrate the feasibility of deploying natural rubber as a low cost ocean wave energy harvester.
Results
Material properties
The basic aptitude of natural rubber for energy harvesting is tested on two example materials based on natural rubber and on commonly used acrylic elastomer. Using commercially available mass products ensures a large material supply chain with identical composition, produced under the quality standards common in industry.This work characterizes the material properties of three off-the-shelf dielectric elastomers. ZruElast A1040 (ZRU)21 is a 300 μm thick natural rubber sheet containing 23 wt% of inorganic fillers and 1.19 wt% of carbon. Oppo Band 8003™ (OP)22 from Oppo Medical Inc. is a 227 μm thick physiotherapy rubber sheet containing 0.96 wt% inorganic fillers and 0.56 wt% carbon.
Oppo Band was selected due to the elasticity and mechanical durability that a physiotherapy band is designed for. The acrylic-based material is 1000 μm thick VHB4910™ from 3M™.23
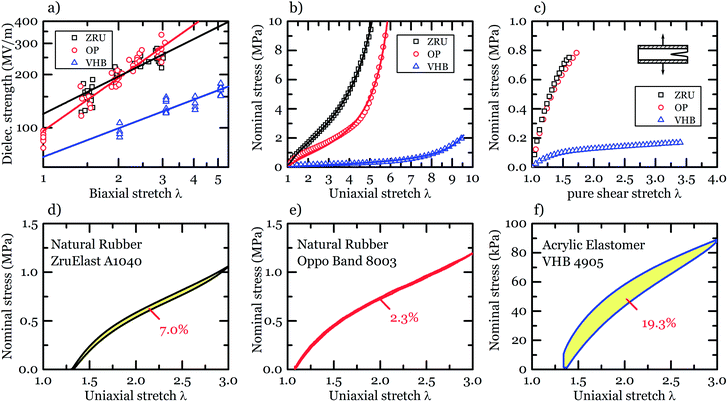
The aptitude of materials for use in soft generators is largely determined by several properties. The dielectric strength EB(λ) and the dielectric permittivity ε determine the amount of electrical energy ∝ εEB(λ)2 that can be stored. Improving the performance of dielectric materials The elastic stiffness and the limiting stretch determine the amount of mechanical energy that can be stored. The ‘mechanical-to-electrical’ energy conversion efficiency is limited by dissipative processes such as viscoelastic hysteresis and charge leakage.24 The toughness of an elastomer is quantified by fracture energy, namely, the energy needed for a crack to advance per unit area. In order to assess the usefulness of the different elastomers for energy harvesting, we experimentally measure the mechanical and dielectric properties of these materials (Fig. 2 and Table 1). The detailed description of the experimental methods used to determine the material parameters is given in ESI† in the section “Experimental methods”.
| Property | VHB™ 4910 | ZruElast™A1040 | Oppo Band™ 8003 |
|---|---|---|---|
| Shear modulus (100%/s) μ [kPa] | 52 | 917 | 466 |
| Gent parameter (100%/s) Jlim | 114 | 44 | 43 |
| Unstretched dielectric strength EB [MV m−1] | 69 | 120 | 97 |
| Strengthening exponent R | 0.54 | 0.70 | 0.99 |
| Relative dielectric permittivity (1 kHz) εr | 4.2 | 3.4 | 2.8 |
Loss tangent (1 kHz) tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ δ |
2.5 × 10−2 | 5.6 × 10−3 | 2.0 × 10−3 |
| Hysteresis loss (5%/s) | 19.3% | 7.0% | 2.3% |
| Fracture energy (100%/s) Γ [kJ m−2] | 3.92 | 6.15 | 7.21 |
The dielectric strength is dependent on the state of stretch, and is much larger in natural rubber than in the acrylic elastomer25 (Fig. 2a). To obtain the intrinsic dielectric strength of the samples we employ the method of Tröls et al.25 preventing any actuation while applying high voltage. Following Koh et al.,26 we fit our experimental data to the expression
| EB(λ) = EBλR | (1) |
Fracture energy indicates the capability of a material to resist the growth of a crack under mechanical load. Fig. 2c shows the nominal stress–stretch relation of samples containing a preexisting crack of 20% of the materials width under pure-shear deformation. The strain at rupture in precut samples is used to obtain the fracture energy as detailed in the methods section. The fracture energy of natural rubber is almost two times that of VHB at a strain rate of 100%/s (Table 1). The fracture energy for VHB is consistent with a previously reported result.20
All of the tested elastomers exhibit large hysteresis losses in the first loading–unloading cycle, which gradually saturates to a lower value from the 5th cycle onwards. This may be attributed to the Mullins effect,28,29 which is most observable in the first few stress cycles of a pristine elastomer, and gradually diminishes for subsequent cycles (details are presented in ESI, Fig. S4†). The different filler material of ZRU affects its dielectric strength and causes plastic deformation at large stretches. In the steady state, the energy loss per cycle is larger in the acrylic elastomer than in the natural rubbers (Fig. 2d–f).
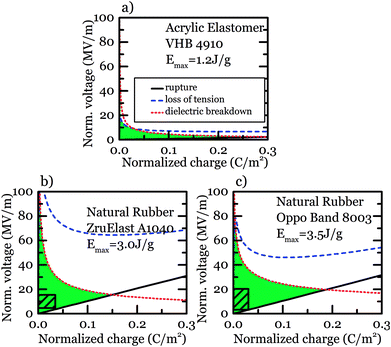
With these material properties, we plot regions of allowable states on work-conjugate planes of voltage and charge30 for the three materials (Fig. 3). The regions of allowable states are determined by lines of maximum biaxial stretch, dielectric breakdown, and states of zero tensile stress (loss of tension). On this plot, any state located within the shaded regions denotes an allowable state, whereas any state located outside are inaccessible due to the occurrence of one or more modes of failure. The area of the shaded region gives the maximum theoretical specific electrical energy that can be generated26 employing biaxial stretch.
The theoretical potential to convert energy of the two rubbers is three times that of acrylic elastomer (Fig. 3). This difference is due to the higher shear modulus and higher dielectric strength of natural rubbers than those of the acrylic elastomer. Direct comparison of OP (3.5 J g−1) and ZRU (3.0 J g−1) reveals a slightly lower conversion capability of ZRU due to lower dielectric strength and maximum stretch.
Material assessment in soft generators
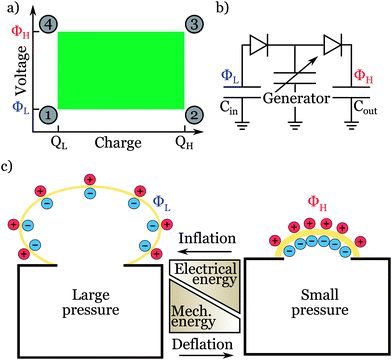
We converted mechanical energy to electrical energy using a particular experimental setup (Fig. 4). We approximately achieved an idealized electromechanical cycle (Fig. 4a) by using a circuit (Fig. 4b) and an air chamber covered with a dielectric elastomer membrane (Fig. 4c). This circuit consists of a low voltage (ΦL) reservoir of charge and a high voltage (ΦH) reservoir of charge, represented by two capacitors of large capacitances Cin and Cout.8,30,31 The two diodes ensure that the electric current only flows from the input to the output reservoir. Several different designs could be employed32 and for an unambiguous measurement of the energy balance a simple design is implemented, such that all useful electric energy is stored in two reservoirs before and after a generation cycle. The two reservoirs, Cin and Cout, are first charged to low and high voltage respectively. Beginning from an uncharged state for the dielectric elastomer generator, charges will flow from Cin to the generator while stretching. The voltage across Cin and the generator will eventually equalize, and charging continues at constant voltage until the maximum mechanical stretch is attained. Here, we ensure that the charges on Cin and Cout are much larger than the maximum charge on the dielectric elastomer generator, such that the voltages on Cin and Cout are only slightly affected by transfer of charges to/from the generator. When the pressure reduces, the dielectric elastomer membrane reduces its area and increases its thickness. Consequently the membrane boosts the voltage until it matches that of the output capacitor, and begins to pump charges into Cout. This process of constant voltage charge pump by mechanical relaxation continues until the membrane is fully relaxed. The cycle is repeated. The corresponding yield of the electrical energy by the soft generator per cycle is:| Wele = ΦHΔQout − ΦLΔQin | (2) |
We deform a flat membrane into a balloon by pressurizing a chamber (Fig. 4c). This technique allows the membrane to undergo equal-biaxial stretching at areas around its apex, which enlarges as the membrane inflates. The mechanical work done on the membrane per cycle of operation is:
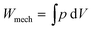 | (3) |
The maximum electrical energy yield Wele is proportional to the volume of the membrane, the dimensions of the membrane are of no importance. Larger thickness linearly increases applicable voltages, while the charge on the membrane remains constant as the increase of voltage is compensated by a decreasing capacity. Increasing the area of the membrane does not affect the voltages, but linearly increases the amount of charge stored on the membrane. A similar argumentation also leads to the conclusion that Wmech is proportional to the volume and thus all energy related quantities can be normalized by the volume of the elastomer membrane and due to incompressibility also by the mass.
By monitoring the voltage Φ, the pressure p and the balloon volume V of the soft generator we can hence track the mechanical and electrical energy flow through the soft generator and determine the specific electrical energy and specific average power.
This method was previously used to assess the aptitude of VHB4910 resulting in a specific electrical energy output per cycle of 102 mJ g−1 and specific average power of 17 mW g−1.8
Energy harvesting using ZruElast™ A1040
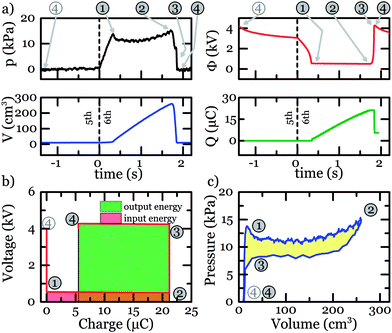
For a lossless membrane under equal-biaxial stretch, energy conversion scales to the fourth power of the stretch – a membrane stretched to two times its original dimensions boosts electrical energy to 16 times the amount of input energy when relaxed. This highly effective manner of energy conversion can be adopted in a diverse range of energy harvesting applications.33–36Fig. 5a shows the generator capacitance change over two orders of magnitude due to the inflation of the membrane during the experiment (represented by open triangles in Fig. 5a). This is in agreement with numerical simulations (red line in Fig. 5a), adapted from Li et al.37Fig. 5b tracks the histories of experimentally determined quantities pressure (p), volume (V), voltage (Φ) on the membrane and net charge (Qnet) transferred to the membrane, during the 6th cycle using the setup introduced in Fig. 4. Many materials experience a stress–strain hysteresis upon cyclic loading which fades to a small value after few cycles. The evolution of the hysteresis loss is presented in ESI, Fig. S4† and shows that from the 6th cycle onward all analyzed materials already experience low hysteresis loss which is comparable to the long term values shown in Fig. 2d–f.
 | ||
| Fig. 5 Experimental generation of electric energy using ZruElast A1040 in a soft generator. (a) The electrical capacitance of the elastomer membrane changes by two orders of magnitude due to inflation. The red line depicts theoretical calculations for capacitance change, showing good agreement with experiment. (b) The recorded pressure, volume, voltage and charge as functions of time during the 6th generation cycle. Encircled numbers mark states of the soft generator corresponding to those in Fig. 4a. (c) Measured generator cycle depicted in the electrical work-conjugate plane. This cycle is not closed due to charge leakage. Charge lost due to leakage results in the gap between the initial charge and the charge at the final point of the cycle. The electrical energy input (148 mJ g−1, red area), and the output (358 mJ g−1, green area) total in net generated energy of 210 mJ g−1. (d) The path depicted in the mechanical work-conjugate plane enclosing an area of 1.4 J g−1 resulting in a ‘mechanical-to-electrical’ energy conversion efficiency of 14.9%. | ||
The 5th cycle ends approximately 7 seconds before the 6th cycle starts with the generator being at a state of high voltage and minimum charge. During this period, leakage currents lead to a slow voltage drop. At t = 0 s the generator cycle starts by inflating the membrane, increasing its capacitance while keeping the charge constant until the voltage matches that of the input reservoir at point 1 (t = 0.67 s). Upon further inflation charge is transferred from the input reservoir to the membrane which reaches its maximum volume and capacitance (pt. 2) at t = 2.29 s.
In the following deflation stage the charge is again confined to the membrane and the voltage increases, reaching the level of the output reservoir at point 3 (t = 2.53 s). Subsequent deflation results in transferring charges from the membrane to the output reservoir, until the minimum volume is reached (pt. 4) at (t = 2.55 s). In this experimental cycle, the specific electrical energy generated was 210 mJ g−1, the mechanical energy consumed was 1.4 J g−1, resulting in a ‘mechanical-to-electrical’ conversion efficiency of 14.9% and a specific average power of 82.4 mW g−1. As some charge leaked through the membrane (6.4 μC) the cycle is not closed since more charge was transferred from the input reservoir (Qin = 23.6 μC) to the membrane than transferred from the membrane to the output reservoir (Qin = 17.2 μC).
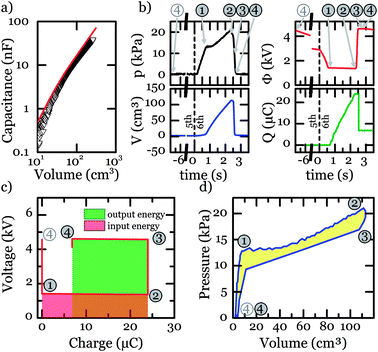
Energy harvesting using Oppo Band™ 8003
The typical conversion cycle depicted in Fig. 3 was also used to assess the aptitude of OP for soft generators and the results are shown in Fig. 6. On the last leg of the 5th cycle (t < 0 s, point 4 of 5th cycle), the voltage at the membrane drops due to charge leakage. The 6th cycle commences upon inflation of the membrane, resulting in a sharp voltage drop that matches the voltage at Cin, given by pt. 1 at t = 0.34 s. Charges transfer from Cin to the membrane at constant voltage up to a prescribed maximum stretch, given by pt. 2 at t = 1.73 s. At this point, the membrane deflates, resulting in an open-circuit voltage boost. The voltage of the membrane matches the voltage of the output reservoir at pt. 3 at t = 1.84 s. After that, charges are transferred to Cout at constant voltage as the membrane continues to deflate until it is flat, given by pt. 4 at time t = 1.85 s. Fig. 4c gives the measured voltage and charge states on the voltage–charge plane. This plot is compared with the ideal cycle in Fig. 4a. It was experimentally observed that the charge transferred from Cin to the membrane (ΔQin = 21.2 μC) is not fully transferred to Cout (ΔQout = 15.7 μC). This represents a leaked charge of 5.5 μC. From (2), the electrical energy yield is 369 mJ g−1. With the cycle time of 1.85 s, the specific average power is 200 mW g−1. From (1), the mechanical energy is 5.1 J g−1, giving a ‘mechanical-to-electrical’ conversion efficiency of 7.2%.These are among the highest experimental values of specific average power and energy reported in the literature for soft generators. Using a different setup with equal biaxial deformation the highest reported value for a soft generator using VHB is 280 mW g−1 and 560 mJ g−1.38
Implications on wave energy harvesting
Existing designs for ocean wave energy harvesting2 currently work at high levelized costs of electricity (LCOE).3 The LCOE is calculated by accounting for all costs within the expected system lifetime, divided by the energy output of the system. Pelamis is the world's first wave energy converter (WEC) that supplies power to electrical grids.39 It consists of long, rigid steel pipes with joints that flex with ocean waves. To convert sufficient energy for power grids, each Pelamis module is about 200 m long, and operates at an LCOE of 26.5–61.7 ct kW−1 h−1.40 Similar to the Pelamis, the Oyster,41 Drakoo, Archimedes wave swing,2 Anaconda,42 point source buoy converter2 and the terminator Salter Duck43 devices simply channel power from waves to drive rotary or linear generators. These generators, known as power take-off systems,44 contribute significantly to the cost of the wave energy converters.45 The cost of steel and concrete is also significant due to costly material production and maintenance in the harsh ocean environment.Here we identify natural rubber as a material for soft energy generators that allow for ocean wave energy harvesting at a potentially low LCOE in the range of 5–11 ct kW−1 h−1, significantly lower than currently available technology. The very high energy density,36,46 the lack of moving parts16 and the inherent impedance matching47 are unique benefits of soft wave energy generators.
The LCOE for soft WECs are estimated based on an analysis of the Pelamis wave energy converter.40,45 The LCOE of Pelamis are modified to match material cost, estimated lifetime and estimated savings on maintenance when using soft materials for the structure and adjusted for the different specific power. Details are available online in ESI, Fig. S2.†
Natural rubber is harvested from plants, has a low carbon footprint48 and low material cost.49 Pará rubber trees (Hevea brasiliensis) exist in abundance Southeast Asia. They are a hardy species, with a single mature tree capable of producing a continuous supply of latex for up to 25 years.50 For example, Thailand, Indonesia and Malaysia, the world's top three producers of natural rubber, produced 7.4 million metric tons of rubber in 2011.49 Natural rubber production is sustainable due to low soil nutrient depletion and the long productive life of rubber trees.
Natural rubber-based generators are very promising due to the low cost of material production and high energy conversion potential. We demonstrated that soft, natural rubber generators have high specific power resulting in systems that are lightweight and low cost. It is observed that the fracture energy is twice as high for rubber compared to VHB at a strain rate of 100%/s. It has been shown in previous works that the fracture energy of amorphous polymers is correlated with their fatigue life against cyclic loading.51 We may hence conclude that both rubbers are more durable against cyclic operation than VHB.
The demonstrated specific power of 200 mW g−1, at a fraction of the costs of current technologies may allow large-scale production of economical, portable and durable mechanical energy harvesting systems. To replace a large power plant (1 GW) the amount of rubber needed is 105 tons assuming a conservative power density on the order of 10 kW t−1. This is only 1% of the annual rubber production.
The key challenges of implementing mechanical energy harvesting systems lie in system size and cost.16 This challenge is particularly important in ocean wave energy harvesting, where wave energy converters must be of low cost and be able to generate energy in isolation. Comparably small wave energy converters with high energy density may enable the harvesting of wave energy close to conurbations with heavy sea traffic leaving the sea channels obstruction-free avoiding long transmission paths.
An alternative lower cost soft material-based wave energy converter16 using natural rubber operates at 28% (5–11 ct kW−1 h−1) of the LCOE of Pelamis. This estimate is based on a detailed analysis of Pelamis45,52–54 which is adapted to the different material and maintenance cost, structure, and power density of a soft wave energy converter. The details of this estimation are found in ESI.† The estimation assumes achieving a real-world power density in ocean environments of only 1% (2 kW per ton) of the maximum power density achieved under laboratory conditions (200 kW per ton). The reason behind this conventional assumption is that a large scale wave energy converter will certainly include additional parts adding to its weight, while operating for a very long lifetime demands for operation under safe conditions reducing the electrical power output. The resulting power density of 2 kW per ton are comparable with the power density reported from wave tank tests of a similar device using silicone rubber (1.1 kW per ton).16
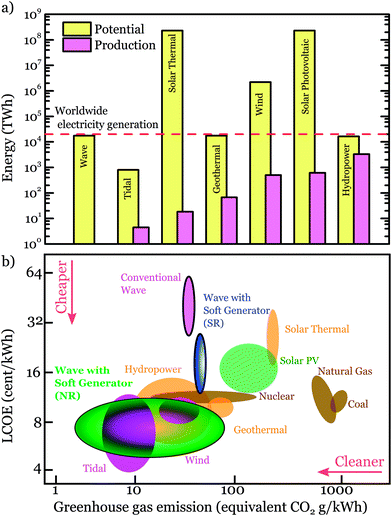
The significance of this result is emphasized by the fact that today no existing technology is capable to tap into the huge resource of ocean wave energy at competitive prices. Fig. 7a compares the potential energy supply and the actual production of different resources to the amount of electric energy generated in 2009 (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 043 TW h).3 Although marine waves provide a huge renewable resource, with a total potential at the same level as the yearly energy needs of the world,55 it is largely untapped.
043 TW h).3 Although marine waves provide a huge renewable resource, with a total potential at the same level as the yearly energy needs of the world,55 it is largely untapped.
Furthermore, the simplicity of production and low maintenance of natural rubber based structures cause greenhouse gas emissions as low as 1.5 g CO2 eq. per kW per h as compared to Pelamis' 28 g CO2 eq. per kW per h.56Fig. 7b compares LCOE and greenhouse gas emissions of different technologies for generation of electricity. Details of the method for estimating the LCOE and a referenced version of Fig. 6 are found online in ESI, Fig. S1–3.†
Conclusion
The discovery of natural rubber as an electromechanical generator creates the possibility of developing mechanical harvesting systems that are sustainable and low in cost. Its high fracture energy promises high durability and lifetime, the outstanding combination of mechanical and electrical properties are responsible for high specific energy and power in soft generators and all this comes in one package in well-known natural rubber at a low material price.The technology can be used to harvest ocean energy to feed into the energy grid as well as harvesting energy from ambient environment to power portable devices and remote sensors. Recent advances in material design using nanoscale fillers enhance permittivity as well as dielectric strength57,58 which could lead to optimized rubber based materials and improve the performance of soft generators, opening up more and more possibilities for soft energy harvesting.
Acknowledgements
The authors are grateful to Dr Zrunek for the kind supply of natural rubbers. The authors from the Johannes Kepler University Linz acknowledge funding from the ERC through the Advanced Grant “Soft-Map” and from the Austrian Science Fund under the DACH-Project FWFI00986000. The authors at Harvard acknowledge funding from the NSF MRSEC (DMR-0820484). Rainer Kaltseis acknowledges funding through a Marshall Plan Scholarship from the Austrian Marshall Plan Foundation. Choon Chiang Foo acknowledges support from A*STAR Graduate Scholarship (Post-doctoral Fellowship). Soo Jin Adrian Koh acknowledges funding support from Ministry of Education (Singapore), for Academic Research Funding (Tier 1), project no.: R302000013133.Notes and references
- G. Hagerman, G. Scott and P. Jacobson, Mapping and Assessment of the United States Ocean Wave Energy Resource, Electrical Power Research Institute, 2011, Technical report 1024637, available at http://www.eere.energy.gov/water/pdfs/mappingandassessment.pdf.
- B. Czech and P. Bauer, Wave Energy Converter Concepts: Design Challenges and Classification, IEEE Ind. Electron. Mag., 2012, 6, 4–16 CrossRef.
- S. Chu and A. Majumdar, Opportunities and challenges for a sustainable energy future, Nature, 2012, 488, 294–303 CrossRef CAS PubMed.
- J. Mullaly, The Laying of the Cable, Or the Ocean Telegraph, D. Appleton and Company, 1858 Search PubMed.
- J. R. Chaplin, et al. Development of the ANACONDA all-rubber WEC, in Proc. 7th EWTEC, 2007 Search PubMed.
- R. Pelrine, et al. Dielectric elastomers: Generator mode fundamentals and applications, Proc. SPIE, 2001, 4329, 148 CrossRef CAS PubMed.
- S. J. A. Koh, Maximum Energy that can be Harvested from a Dielectric Elastomer Generator, in MRS Symp. Z, 2009, vol. 1218E, p. 1218 Search PubMed.
- R. Kaltseis, et al. Method for measuring energy generation and efficiency of dielectric elastomer generators, Appl. Phys. Lett., 2011, 99, 162904 CrossRef PubMed.
- T. G. McKay, B. M. O'Brien, E. P. Calius and I. A. Anderson, Soft generators using dielectric elastomers, Appl. Phys. Lett., 2011, 98, 142903 CrossRef PubMed.
- J. Maas and C. Graf, Dielectric elastomers for hydro power harvesting, Smart Mater. Struct., 2012, 21, 064006 CrossRef.
- T. Vu Cong, C. Jean-Mistral and A. Sylvestre, Electrets substituting external bias voltage in dielectric elastomer generators: application to human motion, Smart Mater. Struct., 2013, 22, 025012 CrossRef.
- T. Li, S. Qu and W. Yang, Energy harvesting of dielectric elastomer generators concerning inhomogeneous fields and viscoelastic deformation, J. Appl. Phys., 2012, 112, 034119 CrossRef PubMed.
- Y. Liu, et al. Analysis and manufacture of an energy harvester based on a Mooney-Rivlin–type dielectric elastomer, EPL, 2010, 90, 36004 CrossRef.
- C. Jean-Mistral, S. Basrour and J.-J. Chaillout, Dielectric polymer: scavenging energy from human motion, Proc. SPIE, 2008, 6927, 692716 CrossRef PubMed.
- I. A. Anderson, T. A. Gisby, T. G. McKay, B. M. O'Brien and E. P. Calius, Multi-functional dielectric elastomer artificial muscles for soft and smart machines, J. Appl. Phys., 2012, 112, 041101 CrossRef PubMed.
- P. Jean, et al. Standing wave tube electro active polymer wave energy converter, Proc. SPIE, 2012, 8340, 83400C CrossRef PubMed.
- F. Carpi, S. Bauer and D. De Rossi, Materials science. Stretching dielectric elastomer performance, Science, 2010, 330, 1759–1761 CrossRef CAS PubMed.
- J. Biggs, et al. Electroactive Polymers: Developments of and Perspectives for Dielectric Elastomers, Angew. Chem., Int. Ed. Engl., 2013, 52, 9409–9421 CrossRef CAS PubMed.
- P. Brochu and Q. Pei, Advances in Dielectric Elastomers for Actuators and Artificial Muscles, Macromol. Rapid Commun., 2010, 31, 10–36 CrossRef CAS PubMed.
- M. Pharr, J.-Y. Sun and Z. Suo, Rupture of a highly stretchable acrylic dielectric elastomer, J. Appl. Phys., 2012, 111, 104114 CrossRef PubMed.
- Zrunek Gummiwaren GmbH, Zrunek Rubber Technology, 2013, at http://www.zrunek.at/uk/ukhome.html.
- Oppo Medical Inc, Oppo Medical | Orthopedic | Oppo Band, at http://www.oppomedical.com/product/detail.asp?serno=260.
- 3M, Industrial Adhesives & Tapes, at http://solutions.3m.com/wps/portal/3M/en_US/Adhesives/Tapes/Products/~/All-3M-Products/Industry-and-Professionals/3M-Tape-and-3M-Adhesives/Double-Sided-Bonding-Tapes/3M-VHB-Tape?Ntt=4910&rt=s.
- C. Chiang Foo, et al. Performance of dissipative dielectric elastomer generators, J. Appl. Phys., 2012, 111, 094107 CrossRef PubMed.
- A. Tröls, et al. Stretch dependence of the electrical breakdown strength and dielectric constant of dielectric elastomers, Smart Mater. Struct., 2013, 22, 104012 CrossRef.
- S. J. A. Koh, C. Keplinger, T. Li, S. Bauer and Z. Suo, Dielectric Elastomer Generators: How Much Energy Can Be Converted?, IEEE ASME Trans. Mechatron., 2011, 16, 33–41 CrossRef.
- A. N. A. Gent, New Constitutive Relation for Rubber, Rubber Chem. Technol., 1996, 69, 59–61 CrossRef CAS.
- F. Bueche, Molecular basis for the mullins effect, J. Appl. Polym. Sci., 1960, 4, 107–114 CrossRef CAS.
- A. Dorfmann and R. W. Ogden, A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber, Int. J. Solids Struct., 2004, 41, 1855–1878 CrossRef PubMed.
- S. J. A. Koh, X. Zhao and Z. Suo, Maximal energy that can be converted by a dielectric elastomer generator, Appl. Phys. Lett., 2009, 94, 1–13 Search PubMed.
- H. U. Fuchs, A surrealistic tale of electricity, Am. J. Phys., 1986, 54, 907–908 CrossRef.
- C. Graf, J. Maas, B. M. Ag & D. Schapeler, Electromechanical Energy Conversion using Dielectric Elastomer Generators, in 12th Int. Conf. New Actuators – ACTUATOR 2010, 2010, pp. 834–837 Search PubMed.
- A. Crossland, P. Wyllie and L. Ran, Mechanical to electrical energy conversion in a hybrid liquid–solid dielectric electrostatic generator, J. Appl. Phys., 2009, 106, 044108 CrossRef PubMed.
- T. Sterken, P. Fiorini, K. Baert, R. Puers & G. Borghs, An electret-based electrostatic μ-Generator, in ISSSAM, 2003, pp. 1291–1294 Search PubMed.
- R. Tashiro, et al. Development of an electrostatic generator that harnesses the motion of a living body (use of a resonant phenomenon), JSME Int. J., Ser. A, 2000, 43, 916–922 CrossRef PubMed.
- R. D. Kornbluh, et al. From boots to buoys: promises and challenges of dielectric elastomer energy harvesting, Proc. SPIE, 2011, 7976, 797605 CrossRef PubMed.
- T. Li, et al. Giant voltage-induced deformation in dielectric elastomers near the verge of snap-through instability, J. Mech. Phys. Solids, 2013, 61, 611–628 CrossRef PubMed.
- J. Huang, S. Shian, Z. Suo and D. R. Clarke, Maximizing the Energy Density of Dielectric Elastomer Generators Using Equi-Biaxial Loading, Adv. Funct. Mater., 2013, 23, 5056–5061 CrossRef CAS.
- J. Scruggs and P. Jacob, Harvesting ocean wave energy, Science, 2009, 323, 1176–1178 CrossRef CAS PubMed.
- M. O'Connor, T. Lewis and G. Dalton, Techno-economic performance of the Pelamis P1 and Wavestar at different ratings and various locations in Europe, Renewable Energy, 2013, 50, 889–900 CrossRef PubMed.
- A. Babarit, et al. Numerical benchmarking study of a selection of wave energy converters, Renewable Energy, 2012, 41, 44–63 CrossRef PubMed.
- F. J. M. Farley, R. C. T. Rainey and J. R. Chaplin, Rubber tubes in the sea, Philos. Trans. R. Soc., A, 2012, 370, 381–402 CrossRef CAS PubMed.
- S. H. Salter, Wave Power, Nature, 1974, 249, 720 CrossRef.
- B. Drew, A. R. Plummer and M. N. Sahinkaya, A review of wave energy converter technology, Proc. Inst. Mech. Eng., Part A, 2009, 223, 887–902 CrossRef.
- M. Previsic, R. Bedard, H. George and O. Siddiqui, System Level Design, Performance and Costs for San Francisco California Pelamis Offshore WavePower Plant, Electrical Power Research Institute, 2006, E2I EPRI Global-006A-SF, available at http://oceanenergy.epri.com/attachments/wave/reports/006_San_Francisco_Pelamis_Conceptual_Design_12-11-04.pdf.
- S. P. Beeby, et al. A micro electromagnetic generator for vibration energy harvesting, J. Micromech. Microeng., 2007, 17, 1257–1265 CrossRef.
- H. Prahlad et al. Polymer Power: Dielectric Elastomers and Their Applications in Distributed Actuation and Power Generation, in ISSS, 2005, pp. 100–107 Search PubMed.
- W. Jawjit, C. Kroeze and S. Rattanapan, Greenhouse gas emissions from rubber industry in Thailand, J. Cleaner Prod., 2010, 18, 403–411 CrossRef CAS PubMed.
- Food and Agriculture Organisation of the United Nations (FAOSTAT), Production of Unprocessed Crops, 2012, at http://faostat3.fao.org/faostat-gateway/go/to/download/T/TP/E.
- M. R. Sethuraj & N. M. MathewNatural rubber: Biology, cultivation and technology, Elsevier Science, 1992, vol. 622 Search PubMed.
- A. Griffith, The phenomena of rupture and flow in solids, Philos. Trans. R. Soc., A, 1921, 221, 163–198 CrossRef.
- C. McGowin, et al. Renewable Energy Technical Assessment Guide—TAG-RE, 2006, Electrical Power Research Institute, 2007, Final report 1012722, available at http://www.epri.com/abstracts/Pages/ProductAbstract.aspx?ProductId=000000000001012722.
- M. Previsic, O. Siddiqui and R. Bedard, Economic Assessment Methodology for Offshore Wave Power Plant, Electrical Power Research Institute, 2004, E2I EPRI WP-US-002 Rev 4, available at http://oceanenergy.epri.com/attachments/wave/reports/002_Rev_4_Econ_Methodology_RB_12-18-04.pdf.
- C. Anderson, Pelamis WEC – Main Body Structural Desgin and Materials Selection, (DTI New and Renewable Energy Programme, 2003).
- K. Gunn and C. Stock-Williams, Quantifying the global wave power resource, Renewable Energy, 2012, 44, 296–304 CrossRef PubMed.
- R. P. M. Parker, G. P. Harrison and J. P. Chick, Energy and carbon audit of an offshore wave energy converter, Proc. Inst. Mech. Eng., Part A, 2007, 221, 1119–1130 CrossRef CAS.
- T. Tanaka, Dielectric nanocomposites with insulating properties, IEEE Trans. Dielectr. Electr. Insul., 2005, 12, 914–928 CrossRef CAS.
- E. Tuncer, et al. Enhancement of dielectric strength in nanocomposites, Nanotechnology, 2007, 18, 325704 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra03090g |
| This journal is © The Royal Society of Chemistry 2014 |