Is surface patch binding between proteins symmetric about isoelectric pH?

Abstract

Surface selective patch binding (SPB) interaction occurring between two protein molecules, bovine serum albumin (BSA) and gelatin B (GB), both having same isoelectric pH (pI ≈ 5) and identical pH-zeta potential profile, was systematically examined. BSA : GB mixing ratio r was varied in the range 0.16–2.00 and ionic strength was varied in the range 0–10 mM, which yielded optimum binding ratio r = 1. The binding profiles produced asymmetric bell-like curves with clearly identifiable pairs of transition pHs: onset of intermolecular interaction, formation of soluble complexes and coalescence of the soluble complexes occurring at pH_c1,2, pH_φ1,2 and pH_m respectively. Since pH_m could be approached from either lower or higher side of pI, these profiles yielded pairs of pH_c and pH_φ values. In fact, we found (pH_c2 − pI) > (pH_c1 − pI), which clearly indicated that initiation of intermolecular associative interaction was not symmetric about pI (pI = pH_m for r ≤ 1, an observation not reported hitherto. Secondly, (pH_φ2 − pI) ≈ (pH_φ1 − pI) implied that the pH at which soluble complexes formed (pH_φ) was always located symmetrically about pH_m, irrespective of the binding ratio. Higher binding affinity determined from higher value of pH_c2 was confirmed from size measurement results. The change in the turbidity maximum Δτ could be correlated as Δτ ∼ I^1/2 implying electrostatic screening of SPB with increase in ionic strength (I). This interaction was modelled using a linear combination of attractive and repulsive electrostatic forces which revealed considerable screening of the interaction potential U, consistent with aforesaid experimental data; ΔU ∼ I^1/2. Further, it is concluded that intermolecular binding in protein–polyampholyte systems is qualitatively different from that in protein–polyelectrolyte class.

---

1. Introduction

Protein–protein interactions play a very significant role in molecular and cellular biology. These interactions are interplay of a variety of physical forces, and are governed by the thermodynamic environment, and the amino acid sequence and structure of the proteins concerned.^1–6 Surface patch binding between protein molecules is of interest and it owes its origin to a combination of surface parameters. The phenomenon of surface patch binding has been observed in a variety of systems where complementary polyions exhibit associative interactions through selective binding of oppositely charged surface patches of one another overcoming the repulsions present between similarly charged sites.^7–12 Thus, intermolecular complex formation gets initiated by surface selective patch binding even though both the polyions carry similar net charge. This situation is often referred to as binding on the wrong side of pH. Protein molecules are often associated with heterogeneously charged surfaces. Hence, protein–protein interactions are highly surface specific; electrostatic interactions depend on surface charge density, whereas both in hydrogen bonding and van der Waals interactions residues present on surface participate exclusively. Thus, the common strategy to determine the complementary binding sites is to examine the surface features of the protein molecules to differentiate a potential binding site (hot spot) from the rest of the protein surface.^13,14 It has been observed that certain identified residues, called hot spots, contribute most to the binding free energy.¹⁵ A combination of protein surface properties can be utilized to predict the probability of surface patch binding between a pair of protein molecules. This type of anomalous binding has been found and reported in a variety of systems.^16–18 SPB mediated associative interactions between proteins and adsorbent having same net charge was studied, by ion-exchange chromatography (IEC), for lysozyme, ribonuclease-A, cytochrome-c and α-chymotrypsinogen systems, and it was observed that such interactions are governed by the characteristics of the solvent medium like, the pH, ionic strength, etc.¹⁶ This was attributed to the heterogeneous charge distribution on the protein surface that facilitated binding though the net charge on the protein may be of the same kind as that of the absorbent. Dynamic light scattering and turbidimetry studies were performed to probe the intermolecular binding between the selected proteins RNAse, lysozyme and BSA, and polyelectrolytes with varying linear charge densities, which clearly established the role of SPB mechanism.^17,18

The effect of ionic strength, polyion persistence length and charge density on SPB binding mechanism has been reported.^19–21 However, little is known about the symmetry of this binding mechanism near the isoelectric or any other reference pH, which we seek to answer in this work. For completeness, the surface selective binding process has been explained through potential energy calculations following a simple model where the interaction potential is assumed to be a linear combination of an attractive and a repulsive Coulombic force. In this article, the terms complexes and aggregates are used interchangeably. Considering the fact that protein–protein interactions have the potential to generate novel biomaterials, the importance of their studies can hardly be stressed enough. In addition, such studies provide basic understanding of specific and non-specific interactions between complementary polyelectrolytes.^1–7

2. Materials and methods

Gelatin B (bovine skin extract, bloom 225 and molecular weight 100 kDa), and BSA (molecular weight 67 kDa) were bought from Sigma-Aldrich chemical company (U.S.A.), which according to supplier had a minimum purity of >98%. It needs to be mentioned that the proteins were not subjected to further purification by dialysis, which would have made these salt free. The salt content of the reference solution (ionic strength or conductivity) was not measured. GB and BSA were used as received without further purification. Salt refers to sodium chloride (NaCl). Other chemicals used were of analytic grade and were brought from Thomas Baker, India. All concentrations mentioned are in w/v except for salt, which is expressed in mM.

Gelatin B aqueous solution at a concentration of 0.75% was prepared by dissolving known amount of the protein powder in double distilled deionized water at 40 °C using a magnetic stirrer for almost 1 to 1.5 hours. BSA aqueous solution at a concentration of 0.75% was prepared by dissolving known amount of the protein powder in double distilled deionized water at 25 °C using a magnetic stirrer for almost 1 hour. These stock solutions appeared optically transparent to the eye. Further, these stock solutions were left for 12 hours at 25 °C to equilibrate. Reacting samples for the experiments were prepared by mixing equal volume of stock solutions, and appropriate amount of NaCl was used to set the ionic strength. The salt concentration was varied from 0 to 20 mM. All procedures were performed at room temperature (25 °C) and relative humidity in the laboratory was less than 50%. Solutions used for different experiments described below were obtained by mixing the GB and BSA stock solutions at appropriate proportions to obtain different protein : polyampholyte mixing ratio r (BSA : GB).

The experimental binding ratios were chosen based on the optimum binding stoichiometry ascertained through an independent experiment. The UV absorbance (UV-vis spectrophotometer, Model CE-7300, Cecil Instruments, UK) of the solutions was measured at λ ≈ 290 nm (maximum BSA absorption wavelength), which yielded a binding curve shown in Fig. 1 that clearly established the optimum binding ratio as r = BSA : GB = 1 : 1. The mixing ratio of other samples was chosen so as to span a broad range of r. Thus, samples with r = 1 : 6, 1 : 3, 1 : 1, 4 : 3, 5 : 3 and 6 : 3 were prepared for further studies.

Fig. 1 Binding plot of BSA and gelatin B measured at 25 °C, clearly showing the optimum binding condition pertained to r = BSA : GB = 1 : 1.

The extent of binding (resulting from intermolecular associative interaction) was inferred from quantitative measurement of solution turbidity, light scattering and electrophoresis data. The change in transmittance (%T) was monitored systematically using a colorimeter (Brinkmann-910, Brinkmann Instruments, U.S.) operating at 450 nm.

Zeta potential measurement was performed on an electrophoresis instrument (model: ZC-2000, Microtec, Japan). In order to minimize the influence of electrolysis on the measurements, molybdenum (+) and platinum (−) were used for electrodes. Also, during the measurements, the cell chamber tap on the molybdenum electrode was kept open to release the air bubbles, for the purpose of reducing their effects on the particle movements. If one uses the zeta potential (ζ) as an approximation of the surface potential φ of a uniformly charged sphere, the theory gives ζ ≅ φ = 4π (σ₀/εκ), where σ₀ is the surface charge density of the particle, and ε and κ are the dielectric constant and Debye–Huckel parameter of the solution, respectively. The relationship between mobility (μ₀) and zeta potential (ζ) is ζ = 4π(μ₀η/ε). Then, μ can be written as μ₀ = σ₀/ηκ where η is the viscosity of the solution.²¹

Dynamic light scattering (DLS) experiments were performed at a scattering angle of θ = 90° and laser wavelength of λ = 632.8 nm on a 256 channel digital correlator (Photocor Instruments, USA) that was operated in the multi-τ mode (logarithmically spaced channels). The goniometer was placed on a Newport (USA) vibration isolation table. The time scale spanned 8-decades, i.e. from 0.5 μs to 10 s. This instrument used a 35 mW linearly polarized He:Ne laser. In all the experiments, the difference between the measured and calculated base line was not allowed to go beyond ±0.1%. The measured intensity auto-correlation functions were analyzed by the CONTIN regression software to check the relaxation time distribution function. The diffusion coefficient D is related to corresponding hydrodynamic radius R_h through the Stoke–Einstein relation given as D = k_BT/(6πη₀R_h), where solvent viscosity is η₀, k_B is Boltzmann constant, and T is absolute temperature. Robustness of the fitting results was decided based on two criteria: sample to sample accuracy, and data reproducibility within the same sample.

3. Results and discussion

At the outset it is necessary to recapitulate some of the physical attributes of both the constituent biopolymers for a better understanding of their binding protocol. GB is a random coil biopolymer of low charge density and small persistence length^22,23 (2 nm) having radius of gyration R_g and hydrodynamic radius R_h given by R_g = 34 ± 3 nm, R_h = 23 ± 3 nm. This implied that the chain stiffness determined from the ratio R_h/R_g = 0.67 could be attributed to a fully flexible chain conformation.^24,25 BSA is associated²⁶ with R_h = 3.5 nm and R_g = 3.1 nm, thus the ratio R_h/R_g = 1.13, whereas for a sphere it should be 1.3. This suggests a near spherical conformation for BSA. Thus, the BSA–GB interaction falls in the general class of colloid–polymer chain interaction. However, it must be realized that the GB molecule, though treated as a chain, is associated with a finite surface, which makes it possible for BSA to bind to it via surface patch binding.

3.1. Symmetry of zeta potential profile

The measured zeta potential as function of pH of the solutions is illustrated in Fig. 2 for BSA, GB and their complex (r = 1), which is quite revealing. Both the protein molecules are associated with same pI = 4.6 ± 0.3, and their zeta potential ζ versus pH profiles are exactly the same within experimental error (±1 mV). Hence, at a given pH they have the same net charge with the same polarity.

Fig. 2 Variation of zeta potential as a function of ΔpH (= pH − pI) for BSA, GB and their 1 : 1 complex. The dotted line defines pI. Note the symmetry in the zeta potential profiles of the two proteins and the asymmetry of the same in their complex state.

This data could be analyzed about the ΔpH = (pH − pI) = 0 line as shown in this figure. Region I is the region where the proteins reside in their protonated state whereas in Region II proteins are present in their deprotonated state. One clear observation can be made from this data: the zeta potential versus pH plot for both the proteins is nearly symmetric about their common pI and their profiles are overlapping. Thus, at a given pH both protein molecules will be endowed with same magnitude and similar polarity of charge. This set the background for further experiments. It was pertinent to examine if the two molecules would bind through any form of electrostatic interaction at all, which we have dealt with in detail and discussed in the following sections. Since we are concerned with the issue of symmetry about pI of the proteins, we shall be using (pH − pI) = ΔpH as the independent variable in further discussions.

3.2. BSA–GB binding symmetry

The intermolecular binding was ascertained from three independent sets of experiments: electrophoresis, turbidimetry and particle sizing. Fig. 2 depicts the zeta potential data measured as a function of solution pH, and for comparison we have included similar data for BSA and GB systems. It is clearly seen that the BSA–GB complex exhibits a pH dependence profile that is asymmetric about pI with preferential binding occurring in Region II, where both the proteins are in their deprotonated state and each carry a net negative charge of almost the same magnitude. Regardless, intermolecular complexes having a large negative zeta potential were formed through SPB interactions.

The pH titration profile yielded a clear picture of intermolecular complex formation through change in the solution turbidity τ (= 100 − %T). Turbidity is a function of molecular size, weight and shape of the scattering moiety present in the sample. Thus, rise in turbidity indicates presence of large aggregates in the dispersion medium. This data is presented in Fig. 3 along with the data for BSA and GB samples. The protein samples exhibit expected pH dependent behaviour: low turbidity away from pI (mostly monomeric dispersion) and high turbidity near pI (dispersion contains aggregates).²⁷ The turbidity of BSA–GB solution was much pronounced with the maximum turbidity reaching a value twice that of individual protein sample. Note that the turbidity maximum observed at pH_m could be approached from either +ΔpH or −ΔpH direction. Thus, there are two pH_c values pH_c1 and pH_c2, and two pH_φ values given by pH_φ1 and pH_φ2. We shall discuss the significance of these later.

Fig. 3 pH titration profile showing turbidity as a function of solution ΔpH (= pH − pI) for BSA, GB and BSA–GB solutions. Note the asymmetry of the titration profile pertaining to the BSA–GB solution.

Note that the turbidity profiles are symmetric about pI for the two constituents whereas the turbidity profile for BSA–GB complex is highly asymmetric, exhibiting preferential binding between the two in their anionic state. This inference is corroborated by the data shown in Fig. 4 where size of the intermolecular complex is shown as function of solution pH. Region I pertaining to the protonated state of the proteins depicts formation of smaller complexes as compared to Region II (deprotonated state) where much larger complexes were formed implying preferential binding in that region. Further, the slope of the binding curve, dR_H/dΔpH, was 35 below pI, whereas above pI, it was 55, an increase of close to 60%, which implied that SPB binding was preferred in Region II. Note that the slope dR_H/dΔpH is a quantitative estimation of binding affinity. In the same figure, the turbidity profile of the pH titration data is shown for comparison, and as before, it is possible to estimate the binding affinity from this data by looking at the (dτ/dΔpH) value. Again below pI (ΔpH < 0), the slope (dτ/dΔpH) = 32 and above pI (ΔpH > 0) it was 40, an increase of close to 25%. Thus, the data presented in Fig. 3 and 4 categorically indicated binding propensity in Region II. It is worthwhile to note that close to pI, the measured hydrodynamic radii were minimum because, in our special treatment of the DLS data, the maximum particle size was restricted to wavelength of incident light (634 nm) in order to meet the Rayleigh criterion. This analysis filtered out large size particles from being included in the particle size distribution. Further, the turbidity registers a decrease in Region II due to selective sedimentation of larger complexes.

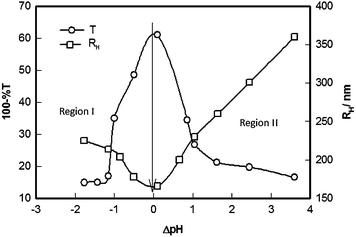Fig. 4 Variation of solution turbidity and size of BSA–GB (r = 1) complexes as a function of solution ΔpH (= pH − pI). The dotted line defines pI, which is coincident with pH_m.

3.3. Effect of ionic strength

It has been long realized that SPB owes its origin to preferential and surface specific electrostatic interactions.^5–12 Thus, it was felt imperative to examine the effect of monovalent counter ions on the screening of abovementioned interaction. This screening is a direct consequence of the formation of an electrical double layer (EDL) around a charged site. A series of pH titrations were carried out, and solution turbidity was monitored systematically. Sodium chloride was added to the protein solutions to control their ionic strengths I in the range I = 0–10 mM. The titration profiles are shown in Fig. S1 (ESI).† Each of these profiles yielded a pair of pH_c values (pH_c1 and pH_c2) and a pair of pH_φ values (pH_φ1 and pH_φ2). These characteristic pH values are plotted as function of solution ionic strength in Fig. 5, which is quite revealing. The maximum turbidity pH_m lies close to pI (dotted line, r ≤ 1) and it defines the symmetry axis. Interestingly, the pH_φ values are very symmetrically placed about this line whereas the same is not true for the pH_c values. This again implies that the SPB interactions are not symmetric about pI. Secondly, it was found that (pH_c1 − pI) < (pH_c2 − pI) which immediately concluded that SPB was sustained even when both the protein molecules were in their highly deprotonated state (large net negative charge). On the contrary, the same was not true when these were in their extreme protonated states (large positive charge). Another observation that could be made was that neither of these characteristic transition pH values exhibited any considerable ionic strength dependence. However, the decrease in the turbidity maximum value Δτ with increase in salt concentration I revealed a dependence which is illustrated in Fig. 6. A least-squares fitting of the data produced the following relationship: Δτ ∼ I^1/2.

Fig. 5 Dependence of characteristic interaction pHs on ionic strength of the solution. Note the location symmetry of pH_φ and asymmetry of pH_c about pI (i.e. ΔpH = 0). Further, pI and pH_m are mostly coincident. The dotted line defines pI.

Fig. 6 Variation of change in turbidity Δτ and interaction potential ΔU shown as a function of square root of solution ionic strength.

As has been stated earlier, turbidity offers a quantitative measure of the size of the scattering entity and a larger size is caused due to stronger interactions. Thus, to a first approximation, turbidity can be assumed to be directly related to intermolecular interaction. It is rather well known that electrostatic interactions are screened in the presence of mobile ions²⁸ considerably and the Debye screening length is given by κ⁻¹ ≈ 0.33/I^1/2 (eqn (3)). Thus, at high ionic strength the electric double layer formed by the mobile ions reduces the Debye screening length. Therefore, electrostatic interactions were weak. On the other hand, at low enough ionic strengths, EDL assumed a finite thickness and electrostatic interactions were facilitated. In the light of this, the experimental observation of Δτ ∼ I^1/2 implied that the BSA–GB interactions were governed by screened Coulomb interactions. Though the strength of the associative interaction decreased with ionic strength, the onset of these interactions did not (see Fig. 5). This will be discussed further when modelling of interaction potential will be dealt with in detail.

3.4. Effect of binding ratio

After having seen the effect of ionic strength on the symmetry of SPB binding, it was felt imperative to examine whether any symmetry existed at all with respect to the BSA : GB binding ratio. A series of pH titrations were carried out on solutions having proteins present in differing binding ratios, which is depicted in Fig. S2 (ESI).† The characteristic transition pH values are plotted in Fig. 7. As before, one found no symmetry in either pH_c or pH_φ profiles about pI; however, with respect to pH_m, the pH_φ profiles are located symmetrically (pI and pH_m were same for ≤1, but deviations towards higher pH was noticed when r ≥ 1. Here again the pH_c1 profile was found to be located closer to pH_m compared to pH_c2. Thus, the general behaviour of various pH profiles was similar to the one shown in Fig. 5. This observation further reinforced the fact that in their deprotonated state these protein molecules were capable to exhibiting profound SPB interaction even when the net charge carried by them was significantly large. Thus, the obtained data lead to the conclusion, without an iota of ambiguity, that SPB was more favoured in the deprotonated state of proteins.

Fig. 7 Behaviour of various transition pHs as function of binding ratio. The vertical dotted line defines the pI of the proteins whereas the horizontal dotted line defines the optimum binding ratio.

3.5. BSA–GB interaction potential

Having observed the phenomena of associative interactions caused by SPB, it was felt imperative to model these forces by accounting for the SPB interaction. This required a priori knowledge of the pH-dependent surface charge and geometrical attributes of protein (BSA) and polyampholyte (GB) used in this study. The experimental data clearly implied that in the deprotonated state (Region II), there was preferential binding compared to Region I. In order to substantiate this we have offered a simple binding model to capture the essential features of this interaction. The said model, though by no means accurate, could qualitatively describe the experimental observation. We present a simplistic molecular level model that adequately describes most of the salient features noticed in BSA–GB interaction. As the protein approaches the oppositely charged polyelectrolyte, the combined effect of Coulombic and van der Waals interactions becomes important. The nature of Coulombic interaction is dependent on polarity and magnitude of interacting charges. On the other hand, the van der Waals interactions are most often attractive and become increasingly stronger as the separation distance is shortened.

Let us consider the protein chain GB as a dipole with the positive and negative charge separated by a distance r (end-to-end length of the chain). The typical radius of gyration R_g of a gelatin B chain is ≈ 34 ± 3 nm, which assigns an effective end-to-end length to the chain √6R_g ∼ 83 nm, whereas BSA is treated as a small dipole of charge q₊ and q₋, having radius of gyration R_g ≈ 3.1 ± 0.5 nm. The size of BSA (6 nm) is very small in comparison to that of gelatin B (83 nm). It is presumed that whole of GB surface is available for interaction with BSA regardless of the fact that some portion of it may be found in a frozen state. BSA can be assumed as a point charge particle having charge q_P. Let R− and R′− be the distances between the negative charge of gelatin B and the negative and positive charges of BSA, respectively, and R′+ and R+ be the distances the positive charge of gelatin B and the negative and positive charges of BSA, respectively, and d is the mean intermolecular distance between the two proteins, as shown in Fig. 8. The protein molecules are essentially amphoteric containing both positive and negatively charged residues. Therefore, simultaneously electrostatic attraction and repulsion between the two protein molecules exist. According to the general model of electrostatic interaction of a protein with a polyelectrolyte,^29,30 the electrostatic attraction and electrostatic repulsion may be related to the average distance between the BSA and GB molecules, and is given by

U = (q_p−/2ε)[[{(Q₋ exp(−kR₊))/R₊}exp(−kR₊) − {(Q₊ exp(−kR₋))/R₋}exp(−kR₋)] (1)

and various distances are related as

R^′₊ ≈ R₊ ≈ d + (r/2)cos Φ and R′₋ ≈ R₋ ≈ d − (r/2)cos Φ (2)

where k⁻¹ is the Debye screening length and Φ is the angular location of the BSA point charge with respect to the GB dipole. The approximation used in using R′+ ≈ R₊ and R′− ≈ R₋ involves an error of only 10% which we consider marginal in this simplistic model. The Debye–Huckel theory defines the screening length as²⁸

k⁻¹ = √(1000εk_BT/(8N_Ae²I)) (3)

where ε is the dielectric constant of the medium. Temperature, elementary charge, Boltzmann constant, and Avogadro's number are represented as T, e, k_B, and N_A, respectively.

Fig. 8 Representative diagram showing the gelatin B and BSA interaction. The curvy line depicts the gelatin B chain that has an end-to-end length = r.

The average intermolecular distance can be found from concentration and molecular weight as

d = [1/(N_BSA + N_GB)]^(1/3) (4)

the approximate number densities of BSA and gelatin B in solution, N_BSA and N_GB, are

N_BSA = (N_A/100) × (C_BSA/M_BSA) and N_GB = (N_A/100) × (C_GB/M_GB) (5)

where C_BSA, C_GB, M_BSA and M_GB are the concentration and molecular weight of BSA and gelatin B molecules, respectively.

The van der Waals and electrostatic interactions of the protein and the polyelectrolyte at various average distances between BSA and GB are shown in Fig. 9, which shows that there is very small contribution of van der Waals interaction, so herein we focus only on the changes occurring due to the electrostatic interaction.

Fig. 9 Plot of electrostatic and van der Waal interaction potentials as function of average intermolecular separation with Debye screening parameter κ = 0.001.

The intermolecular distance d was estimated to be ∼20 nm. The total positive and negative charge on the protein was sum of the contributions arising from all the protonated and deprotonated amino acid residues at a given pH. Angle Ø was varied between 0 and π, but for a range of angles 60° < Ø < 90°, typically the interaction potential increased sharply making the system unstable. For optimum binding condition Ø assumed a value close to 60 °C. The intermolecular separation and charge on BSA and GB chains are known (from their zeta potential data), which makes it possible to obtain potential energy of interaction U operating between these two biopolymers. Since q_P, Q+, Q−, R+, and R− are independent of salt concentration, the presence of salt leads to Coulombic screening through k. This is shown in Fig. 9 for various salt concentrations.

A deeper minimum was observed in low ionic strength solutions, and relative change in the minima of the potential ΔU with ionic strength was plotted as function of I^1/2 in Fig. 5. Remarkably, this data could be least squares fitted to a straight line alike the turbidity versus I^1/2 data. The close ionic strength dependence similarity observed between turbidity and interaction potential could be explained as follows: two molecules exhibiting strong associative interactions will lead to the formation of intermolecular aggregates which will have high solution turbidity. This makes the interaction potential and turbidity directly proportional to each other to a large extent, and hence, Fig. 5 data provides a clear manifestation of this correlation.

Further, the interaction potential revealed two characteristic features: (i) it has a minima invariant of salt concentration located at 16 nm which happens to be the average intermolecular separation and (ii) the potential gets screened with increase in ionic strength of the solution, while in the low salt regime (NaCl < 7.5 mM) it exhibits a weak dependence. The minima vanish for solutions with NaCl > 10 mM. Beyond 20 mM NaCl, no binding transition was noticed in our experiments. Thus, we find close resemblance between the predictions made by the simple model and experimental data.

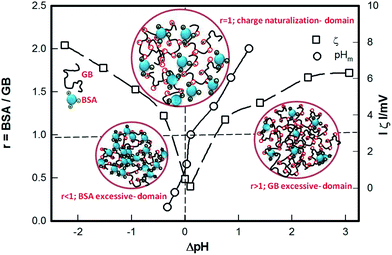
The data in hand clearly indicated differential binding behaviour between the two proteins which is schematically represented in Fig. 11. For r < 1 and ΔpH < 0, the binding was weak; as ΔpH increased to approach 0, optimum binding between the two proteins was observed, which led to the formation of BSA–GB complexes that had low zeta potential values. And for r > 1 and ΔpH > 0, disproportionate binding occurred as a result of which large complexes having sizable zeta potential values were formed in the system. It is to be noted that though ΔpH and r are treated as independent variables, any change in ΔpH has a corresponding impact on r (through the extent of binding). This has been depicted in Fig. 10.

Fig. 10 Plot of interaction potential as function of average intermolecular separation. Note the screening of the potential with increase in solution ionic strength.

3.6. Significance of pH_c and pH_φ

The two classes of protein–polyion interactions observed in nature can be classified into protein–polyampholyte and protein–polyelectrolyte systems. Protein–DNA interactions are an example of the protein–polyelectrolyte class whereas protein–protein interactions belong to the protein–polyampholyte class. In protein–polyelectrolyte systems, it is believed that pH_c is governed by anisotropy of the protein surface charge distribution, which permits binding on the wrong side of pI.³¹ This implies that the charged patch on the protein surface has a different charge density as compared to its global charge density. In comparison, formation of soluble complexes occurring at pH_φ demands that the hydrated complex is electrically neutral, i.e. the charge of the bound protein molecules compensates the charge on the polyelectrolyte. Thus, sometimes it is suggested that pH_φ depends on the net charge of the protein.³² For instance, BSA binds to poly(acrylamidomethylpropyl sulfonate)³³ polyanion at pH_c − pI = 2 whereas β-lactoglobulin (BLG) binds³⁰ to the same polyelectrolyte at pH_c − pI = 1. Both BSA and BLG are associated with identical pI values (4.9 vs. 5.2); however their anisotropic surface charge distribution causes differential binding affinity to the same polyelectrolyte. In the present work, we have shown that in its protonated state BSA binds poorly to GB implying presence of a limited number or smaller charged patches on protein surface. At pH_c1 the zeta potential on the BSA–GB complex was 6 mV and at pH_c2 it was −11 mV. The individual values of the same for BSA and GB at the same pHc₁ were ≈12 ± 1 mV. On the other side of pI, we observed that at pHc₂ the BSA–GB complex had a zeta potential ≈ −17 mV with the corresponding individual values being ≈ −15 ± 1 mV. Thus, regardless of high net charge of same polarity, the two proteins could bind efficiently in the protonated state. Therefore, in the deprotonated state the aggressive binding observed must have originated from the propensity of such charged patches (hot spots) on the BSA surface. Nonetheless, for the binding to occur, the hot spot on protein surface must provide charge complementarity with the flexible GB chain whose linear charge sequence and persistence length ultimately decide the probability of occurrence of any binding (Fig. 11).

Fig. 11 Schematic showing the binding between the two proteins at different pHs and binding ratios.

Let us turn our attention to the pH_φ values which were found to be symmetrically placed about pH_m. We found that formation of soluble complexes was facilitated through SPB interaction regardless of the protein net charge which implied that pH_φ was invariant of protein net charge. Neither could we find any correlation between pH_c and pH_φ values. This raised the pertinent question: what caused the sharp rise in turbidity at pH_φ? The data in hand allows us to propose the following. The propensity of hot spots (complementary charge patches) on BSA surface increases with pH in a disproportionate manner. For pH < pI, this is low whereas for pH > pI it is very high. But the observed fact that (pH_m − pH_φ1) ≈ (pH_m − pH_φ2) established that only a few hot spots on BSA surface need to be bound to GB chain to produce soluble complexes, and charge neutralization may not necessarily be achieved in this process. In our experiments, this was achieved when (pH_m − pH_φ1) ≈ (pH_m − pH_φ2) < 1 pH unit. The typical zeta potential of the complex at pH_φ1,2 was ≈ ±7 mV, which clearly indicated that these complexes were not fully charge neutral. At this pH, the individual proteins had zeta potential value ≈ ± 10 mV. The aforesaid characteristics clearly differentiated the binding between the two systems: protein–polyampholyte and protein–polyelectrolyte.^34–36

4. Conclusions

A series of well-defined and controlled experiments were carried out in order to ascertain the symmetry of surface patch binding about the pI of the proteins concerned. The optimum binding between BSA and GB occurred at the stoichiometric ratio 1 : 1. The associative interactions observed through the monitoring of the solution turbidity generated a bell shaped turbidity–pH profile with maximum turbidity occurring at pH_m (close to pI for r = 1) in both salt-free and salty solutions. For r > 1, pH_m shifted towards higher pH (pH_m > pI) values. Thus, pH_m could be approached from either side of pI regardless of the r-value. This feature established the presence of two uniquely identified transition pHs: (i) pH_c where the initiation of associative intermolecular interactions ensued and (ii) pH_φ where soluble complexes were formed. Needless to say the titration profile yielded a pair of values for pH_c and a pair of values for pH_φ. The pH_φ1 and pH_φ2 values were found to be placed symmetrically about pH_m, whereas no such behaviour was exhibited by pH_c1 and pH_c2 values. In fact, we found (pH_c2 − pI) > (pH_c1 − pI), which clearly indicated that SPB driven initiation of intermolecular associative interaction was not symmetric about pI. Secondly, (pH_φ2 − pI) ≈ (pH_φ1 − pI) implied that the transition pH where soluble complexes formed (i.e. pH_φ) was always located symmetrically about pH_m. Further, it was observed that complete charge neutralization was not achieved at pH_φ1,2, and pH_φ and pH_c were uncorrelated.

It is highly possible that self-interaction occurs, leading to GB–GB and BSA–BSA (smaller aggregates) aggregate formation along with the existence of bigger GB–BSA complexes. Then the system comprises a set of three complexes present in varying ratios depending on the ionic strength, concentration, aging etc. at any point of time. Binding in Region I and Region II are quantitatively different. BSA–GB binding in Region I is driven by SPB that causes charge neutralization and formation of smaller complexes. In their deprotonated state (Region II), this binding proceeds beyond the charge neutralization boundary to cause disproportionate binding. Realize that even at the charge neutralization point there exist residual favorable binding sites that provide further binding, and this has been observed in DNA–protein binding earlier.²⁰ For example, DNA and Gelatin A exhibited disproportionate binding and formed a variety of complex coacervates.³⁷ The complex formed comprises GB–GB and BSA–BSA aggregates (self-interaction) and aggregate BSA–GB aggregates. It is well known that SPB interaction between a pair of polyions can cause coacervation due to associative interaction. Thus, the presence of coacervates is a good indicator of polyion–polyion interaction. We successfully collected the coacervate corresponding to ΔpH = −1, 0 and +2. This clearly implied that the complex formed comprised both protein molecules. Neither BSA–BSA nor GB–GB aggregation will lead to the phenomena of coacervation. We can see that the coacervation yield is more in Region II which is an indicator of intensity of coacervation. This has been clearly depicted in Fig. S3 (ESI).† This is a significant observation considering that in protein–polyelectrolyte systems, at pH_φ, charge neutralization was invariably seen. Thus, intermolecular binding in protein–protein systems are qualitatively different from that in protein–polyelectrolyte systems. The abovementioned conclusions can be summarized as follows: proteins can interact with other protein molecules via an array of secondary interactions. Clear definition of these intermolecular interactions requires a molecular level understanding. However, for native state aggregation, self-association of proteins in their secondary structure conformation is primarily mediated by electrostatic effects. The depletion of Coulombic forces at pI is relevant because charge anisotropy can drive “isoelectric precipitation”, as demonstrated by turbidity maxima commonly observed near the pI. The present study is important for the better understanding of the aforesaid mechanisms. These results can have considerable bearing on the stabilization, separation, and hence protein purification processes.

Acknowledgements

JP acknowledges University Grants Commission, Government of India, for a Junior Research Fellowship.

References

1. T. Vinayahan, P. A. Williams and G. O. Phillips, Biomacromolecules, 2010, 11, 3367–3374.
2. M. Antonov, M. Mazzawi and P. L. Dubin, Biomacromolecules, 2010, 11, 51–59.
3. C. G. de Kruif, F. Weinbreck and R. de Vries, Curr. Opin. Colloid Interface Sci., 2004, 9, 340–349.
4. A. B. Kayitmazer, D. Seeman, B. B. Minsky, P. L. Dubin and Y. Xu, Soft Matter, 2013, 9, 2553–2583.
5. N. Pawar and H. B. Bohidar, J. Chem. Phys., 2009, 131, 045103.
6. L. Tercinier, A. Ye, S. Anema, A. Singh and H. Singh, J. Colloid Interface Sci., 2013, 458–466.
7. S. G. Anema and C. G. (Kees) de Kruif, Soft Matter, 2012, 8, 4471–4478.
8. F. E. Regnier, Science, 1987, 238, 319–323.
9. R. K. Hallberg and P. L. Dubin, J. Phys. Chem. B, 1998, 102, 8629–8633.
10. C. L. Cooper, A. Goulding, A. B. Kayitmazer, S. Ulrich, S. Stoll, S. Turksen, S. Yusa, A. Kumar and P. L. Dubin, Biomacromolecules, 2006, 7, 1025–1035.
11. P. M. Biesheuvel and M. A. Cohen Stuart, Langmuir, 2004, 20, 2785–2791.
12. A. Wittemann and M. Ballauff, Phys. Chem. Chem. Phys., 2006, 8, 5269–5275.
13. R. de Vries, F. Weinbreck and C. G. de Kruif, J. Chem. Phys., 2003, 118, 4649–4659.
14. J. M. Park, B. B. Muhoberac, P. L. Dubin and J. Xia, Macromolecules, 1992, 25, 290–295.
15. J. Konc and D. Janezic, J. Chem. Inf. Model., 2007, 47, 940–944.
16. V. Lesins and E. Ruckenstein, Colloid Polym. Sci., 1988, 266, 1187–1190.
17. J. Gao, P. L. Dubin and B. B. Muhoberac, J. Phys. Chem., 1998, 102, 3830–3836.
18. W. Kopaciewicz, M. A. Rounds, J. Fausnaugh and F. E. Regnier, J. Chromatogr., 1983, 266, 3–21.
19. S. Boral and H. B. Bohidar, J. Phys. Chem. B, 2010, 114, 12027–12035.
20. K. Rawat, J. Pathak and H. B. Bohidar, Phys. Chem. Chem. Phys., 2013, 15, 12262–12273.
21. D. R. Caffrey, S. Somaroo and J. D. Hughes, Protein Sci., 2004, 13, 190–202.
22. H. Ohshima, Adv. Colloid Interface Sci., 1995, 62, 189–235.
23. I. Pezron, M. Djabourov and J. Leblond, Polymer, 1991, 32, 3201–3210.
24. A. N. Gupta and H. B. Bohidar, J. Phys. Chem. B, 2007, 11, 10137–10145.
25. A. Tiwari, S. Bindal and H. B. Bohidar, Biomacromolecules, 2009, 10, 184–189.
26. K. Rawat and H. B. Bohidar, J. Phys. Chem. B, 2012, 116, 11065–11074.
27. Y. Xu, D. Seeman, Y. Yan, L. Sun, J. Post and P. L. Dubin, Biomacromolecules, 2012, 13, 1642–1651.
28. C. Tanford, Physical Chemistry of Macromolecules, Wiley, New York, 1961.
29. E. Seyrek, P. L. Dubin, C. Tribet and E. A. Gamble, Biomacromolecules, 2003, 4, 273–282.
30. T. Hattori, R. Hallberg and P. L. Dubin, Langmuir, 2000, 16, 973–981.
31. C. Cooper, A. B. Kayitmazer, S. Turksen and P. L. Dubin, Curr. Opin. Colloid Interface Sci., 2005, 10, 52–78.
32. M. Antonov, M. Mazzawi and P. L. Dubin, Biomacromolecules, 2009, 11, 51–59.
33. K. W. Mattison, P. L. Dubin and I. J. Brittain, J. Phys. Chem. B, 1998, 102, 3830–3836.
34. K. Kaibara, T. Okazaki, H. B. Bohidar and P. L. Dubin, Biomacromolecules, 2000, 1, 100–107.
35. B. L. H. M. Sperber, M. A. Cohan stuart, H. A. Schols, A. G. J. Vorage and W. Norde, Biomacromolecules, 2010, 11, 3578–3583.
36. J. Van der Gucht, E. Spruijt, M. Lemmers and M. A. Cohen Stuart, J. Colloid Interface Sci., 2011, 361, 407–422.
37. N. Arfin, V. K. Aswal and H. B. Bohidar, RSC Adv., 2014, 4, 11705–11713.

---

Footnote

† Electronic supplementary information (ESI) available: The pH titration profiles showing turbidity and coacervation yield as a function of solution pH for BSA–GB solutions at various ionic strengths and mixing ratios examined in this study are included. See DOI: 10.1039/c4ra02372b

---