Cooperative manipulation and transport of microobjects using multiple helical microcarriers

Abstract

Manipulation and transport of microscale objects in 3D with high spatiotemporal resolution require precise control over the applied forces. We report a strategy that uses specially engineered microbars having engagement points and multiple helical microcarriers that can apply reversible loads onto these holders. The helical microcarriers are actuated by externally generated, low strength magnetic fields. By optimizing the design of helical structures for precise manipulation, we fabricated microcarriers that swim with little wobbling even at low rotating frequencies. The cooperation of microcarriers generates higher propulsive forces while application of forces at multiple locations results in motion control with multiple degrees of freedom (DOF). The microbar loaded with multiple microcarriers can be employed as a single mobile device for the realization of higher order manipulation tasks.

---

Introduction

The controlled manipulation, transport and assembly of biological cells and microscale particles play an important role in many biological, engineering and colloidal science applications.^1–4 Untethered, wirelessly controlled devices offer a less invasive alternative for micromanipulation and can enable new procedures never before possible.^5–10 Several technologies have been introduced to power these devices,^11–18 with the vast majority utilizing magnetic fields.^19–27 Using magnetic helical microstructures, rotating uniform magnetic fields can be transduced into forward motion.^28–30 This propulsion technique has proven to be more efficient than pulling directly with magnetic field gradients,²⁹ and various different fabrication techniques have been introduced for generating swarms of helical microstructures.^31–37

Previous work has shown that helical microstructures can manipulate microscopic objects either directly by mechanical contact or indirectly by generating a localized fluid flow.^33,38 However, these prototypes cannot easily perform delicate manipulation and precise transport due to wobbling at low frequencies.³⁹ The motion stabilizes at high frequencies but precise control of transport becomes a challenge at high swimming speeds due to generated fluid flow. Another important limitation is the uncontrolled motion of cargo during transport. Helical structures with a microholder can be fabricated to form a confined volume for the cargo.³³ This strategy proved to be an improvement, but only objects that are small enough to fit into the holder can be stably transported. A more versatile and reliable manipulation strategy is required to transport arbitrarily shaped microobjects to the desired locations with predetermined alignment.

In this work, we introduce helical microcarriers that have ring-shaped structures on both ends of the helical body. The new design increases the fluidic drag and improves the alignment of magnetization, which together result in smooth motion during swimming. We first demonstrate different direct contact and non-contact manipulation strategies for the transport of microobjects with single microcarriers. Even though these manipulation strategies show promise, it is still difficult to precisely control both translation and rotation during cargo transport with a floating-point contact between the carrier and the microobject. Here, we employ an alternative strategy to address this problem. Microbars with small engagement points and swimmers that can stably load onto these appendages are fabricated. Through this coupling, we demonstrate the reversible loading of multiple microcarriers onto the same microbar. As a result of the stable engagement and cooperation, both the capacity and the precision of manipulation are improved. Microbars with sizes significantly larger than the individual carriers are transported along user-defined trajectories and placed at target locations in desired configurations.

Results and discussion

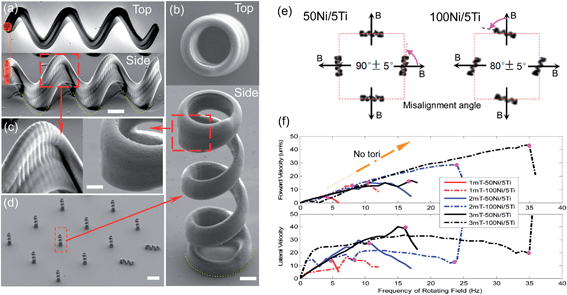
The helical microcarriers were fabricated using 3D direct laser writing (DLW) in vertical arrays. After the development step, a thin layer of Ni and Ti was deposited on the surface of the structures by electron beam evaporation (for details see ESI†). The carriers were finally coated with PLL-g-PEG polymers to prevent adhesion to cargo during transport. We chose vertical writing, as the fabricated structures have more uniform shapes and smoother surfaces compared to horizontal arrays (Fig. 1(a)–(c) and ESI Fig. S1†). These deformations and imperfections can result in wobbling in individual carrier motion and loss of synchrony in collective tasks (ESI Movie M1†). Previously reported helical swimmers had a bare helical shape or consisted of a helical body with a microholder at one end. Due to the magnetization direction of the helical shape, the swimmers wobble about their helical axis during swimming at relatively low frequencies. In addition, the single contact point of helical shape is not strong enough to keep structures standing on the substrate during development (ESI Fig. S1†). Therefore, the structures occasionally fall on the surface and this phenomenon can cause a further shift in the easy axis of magnetization during physical vapor deposition of magnetic materials.

Fig. 1 Fabrication of microcarriers and characterization of their swimming properties. (a) SEM images of a bare helical structure that was written horizontally using IP-L photoresist. (b) The vertically written helical microcarrier from SU-8. The scale bars are 2 μm. (c) Comparison of texture features of designs shown in (a) and (b). The scale bar is 1 μm. (d) A horizontal array of helical microcarriers. The scale bar is 20 μm. The alignment of magnetization angle (e) and swimming performance (f) of same-sized carriers coated with different thicknesses of magnetic material.

We addressed all these problems by introducing ring-shaped structures on both ends of the helical body. First, with the rings the misalignment angle approaches 90 degrees (see Fig. 1(e)). The misalignment angle is defined as the angle between the external field B and the helical axis. Secondly, the ring at the bottom acts as a support for firm attachment during development, and both rings serve to minimize wobbling by increasing the drag force. The increase in drag force slows the swimmer, but speed is not critical for precision manipulation tasks (see Fig. 1(f)). Finally, as an improvement to the sharp tips of bare helical shape, the symmetrical rings on both ends act as connection hubs for stable engagement with target objects.

We studied the role of magnetic material thickness on misalignment angle and swimming performance. The solid circles in Fig. 1(f) depict the step out frequencies (f_step-out) at different magnetic field strengths for two different conditions. For the same sizes, microcarriers coated with 100 nm Ni layer have lower misalignment angles (Fig. 1(e)) and higher f_step-out (Fig. 1(f)). In our experiments, we observed no difference in forward swimming speed with changing thickness. For the rest of the paper, we used microcarriers with 50 nm Ni coating. We fabricated microcarriers having a length about 3.7 times their width. This ratio was reported as optimal for swimming efficiency.⁴⁰ With the optimized design, the fabricated microcarriers can be precisely maneuvered even at very low speed, and the performance does not change from carrier to carrier which allows synchronized movement of swarms and collective transport.

Helical microcarriers can manipulate microobjects in two different ways: either by direct contact or through the generated fluid motion. Previous work addressed the hydrodynamic analysis of rotating twisted ribbon shaped helical structures and nanowires for trapping single objects.⁸ The level of pressure applied to the cargo can be estimated from the velocity gradients using Stoke's law (∇p = η∇²u + f) where the pressure, velocity vector field, viscosity and body forces acting on the fluid are denoted as p, u, η and f, respectively. For a single right-handed microcarrier moving parallel to the surface, the upper-right corner of the helix is favorable for pushing due to the higher pressure levels, while in the lower-left area there exists a vacuum that applies a pulling force within a certain range (see ESI Fig. S2†).

Microbeads have been used as a standard target for manipulation, but they have a symmetrical shape. We fabricated microbars to study both translational and rotational motion of the cargo during transport and develop novel manipulation techniques. The microcarriers showed excellent swimming performance as expected with no detectable wobbling at low speed. In our experiments, we determined four different ways to manipulate and transport microbars (Fig. 2 and ESI Movie M2†). The motion of the microbar depends on the approach angle and 3D confirmation of the microcarrier, as expected. Even though these strategies resulted in some control over the position and alignment of the microbar, experiments with single carriers that are not firmly attached to the cargo demonstrated that precise manipulation is challenging and time-consuming. Furthermore, there is a limit on the size and weight of the microobjects that can be transported.

Fig. 2 Schematic description and experimental demonstration of four basic ways to push a bar on the surface of the substrate (a) a microcarrier pushes one end of the bar to rotate 90 degrees using its head directly with another end of the bar as center. (b) The slight drift generates the pushing force acting on the bar. (c) The bar is conveyed by a microcarrier that was tilted 15 degrees up from the surface. (d) The bar is pushed and rotated by lateral fluid flow. The dots are reference points and the scale bar is 100 μm.

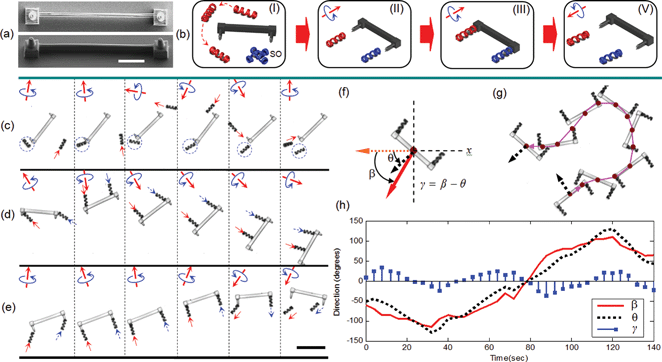
As an alternative approach, we explored the possibility of using multiple microcarriers for cooperative transport (see ESI Movie M2†). Microcarriers with different f_step-out were fabricated by changing the thickness of the Ni layer according to the characterization given in Fig. 1(f). Selective addressing of individual microcarriers can be realized by changing the rotational frequency, and multiple carriers can be localized around the microbar. However, during manipulation, cooperative action was frequently interrupted by the disturbances caused by uncontrollable lateral drift. Therefore, a more reliable manipulation strategy is required for synchronizing the motion of several carriers. We fabricated microbars with supporting microstructures on both ends to be used as loading ports for carriers as shown in Fig. 3a. The design of the handles matches the ring-shaped heads of the microcarriers and allows for stable loading. Handles with half of the length and two thirds of the diameter of a carrier resulted in convenient and stable loading.

The cooperative manipulation strategy is schematically described in Fig. 3(b). The first step is to position the microcarriers at predetermined locations by using f_step-out as a method to selectively deactivate carriers. To achieve this selective deactivation, we first position the microcarrier with a lower f_step-out and then increase the frequency to move the second carrier to its desired location while the first carrier is in a stationary mode. In the second step, microcarriers are steered towards the microbar with a desired orientation to load them properly onto the microbar. The microbar is then transported to the target location. Finally, the carriers can be disengaged from the bar by reversing the rotational direction of the magnetic field, and the carriers become free for the next manipulation task.

Fig. 3 Cooperative manipulation using multiple microcarriers. (a) SEM image of a microbar fabricated with handles. (b) Schematic description of the cooperative manipulation strategy. (c) Snapshots from the recorded videos showing the positioning of multiple carriers around the microbar. The carrier in blue circle cannot move as the rotating frequency of the magnetic field is higher than its step out (SO) frequency. (d) Moving the microbar with two carriers without firm attachment. (e) Loading and unloading of microcarriers. (f) Steering direction of the microcarrier. The horizontal dashed line is a reference line with 0 degree. (g) The trajectory of the microcarrier transported with loaded microcarriers. The angular error between the expected and recorded orientation of the microbar remains lower than ±50 degrees throughout the experiment. The scale bars are 20 and 100 μm.

The experimental demonstration of the described strategy is given in Fig. 3(c)–(e). Compared to stable loading (Fig. 3(e)), microbars transported with unbound microcarriers (Fig. 3(d)) show deviations from desired orientation during transport. In Fig. 3(e), the last three steps of the cooperative manipulation strategy was demonstrated; loading, cargo transport, and unloading. Both carriers were simultaneously loaded/unloaded to the bar using low rotating frequencies. By coupling the carriers to the microbar, we form a single body powered by several magnetically actuated propellers. This strategy takes multiple propulsion signals as inputs and transforms them into a single, coherent movement (Fig. 3(f)). The orientation of the microbar follows the direction of thrust generated by the rotating magnetic field, and the difference between these two angles (γ) stays within certain range (below ±40°). To prevent unloading of microcarriers due to sharp turns, the angular velocity of the whole body should obey the following formula: ω_max ≤ ν/r_bar.

We combined all the described manipulation strategies (contact and non-contact manipulation with single carriers and cooperative manipulation) to demonstrate the versatility and precision of the methodology (see ESI Movie M3†). Several identical microbars were transported to specific locations with pre-defined orientations to write the letters “ETH” (Fig. 4). For cooperative transport, we employed carriers with different Ni coatings (50 and 100 nm), and for lateral push we used carriers with relatively larger rings (see ESI Fig. S1†). Initially, all the bars were randomly distributed on the substrate as shown in the inset of Fig. 4(d). We first assembled the letter ‘E’ by with collective effort of two microcarriers (Fig. 4(a)). For the assembly of letter ‘T’ (Fig. 4(b)), we combined cooperative manipulation with the non-contact lateral push as described in Fig. 2(d). The letter ‘H’ was assembled using several direct contact and non-contact manipulation techniques from Fig. 2. Fig 4(d) shows the final product.

Fig. 4 Several different contact and non-contact manipulation strategies were combined in a single experimental demonstration. (a–d) ‘ETH’ logo assembled using cooperation of multiple microcarriers. The purple lines show the trajectory and orange arrows show the direction of motion. The scale bar is 100 μm.

Viscous forces dominate and inertia is negligible at low Reynolds numbers.²⁸ A propulsion matrix linearly relates force and torque of the carrier with its forward velocity and angular speed. For the microcarriers, the parameters in this matrix are functions of turn numbers, helical angle, pitch, radius and the resistive force coefficients parallel and perpendicular to the axis of helix. The drag force acting on each ring-shaped structure of a helical microcarrier can be approximated by a rotating torus in a uniform Stoke's flow. Assuming that the microcarriers are sufficiently far from each other and there is no fluidic interaction, we can estimate the non-fluidic force applied to the cargo during cooperative transport. If the rotational frequency of magnetic field is held constant at all times, then the drag force on the payload can be formulated as

See ESI† for the details of the derivation of (1). By measuring the forward velocity, we can estimate the drag force on the microbar during transport. The experimental results show that the microbar (100 × 10 × 8 μm) moves with a velocity of 3 μm s⁻¹ at a rotating frequency of 8 Hz, and from (1) the total drag force is calculated as 200 pN. Using this analysis, we can estimate the drag force on any arbitrarily shaped microobjects transported by microcarriers.

Conclusions

In this work, we focused on micromanipulation and determined the requirements for the manipulation of arbitrarily shaped microobjects. We demonstrated a new methodology to reliably load and unload several microcarriers on the same target object to improve dexterity, precision and power of manipulation. We performed four different contact and non-contact manipulation strategies with single microcarriers and combined them altogether to reliably transport and orient many microobjects with multiple microcarriers. These initial results will open up many exciting opportunities for the multi-DOF manipulation of arbitrarily shaped microobjects in 3D for microassembly and targeted delivery tasks. We can consider the microbar loaded with multiple carriers as a single micromachine. With this micromachine, it will be possible to precisely manipulate arbitrarily shaped objects that have no engineered holders required for loading of carriers. Helical structures generate vortices that can damage delicate cargo during transport. However, there exists a direct contact push area in front of the micromachine where the flow is steady. Depending on the shape of the micromachine and the locations of the handles, a variety of different manipulation strategies can be implemented in 3D. The cargo can be fabricated from biocompatible and biodegradable materials, which could lead to targeted delivery of drug and cell loaded scaffolds using a swarm of helical microcarriers.⁴¹

Materials and methods

Fabrication of helical microcarriers and microbars

The microcarriers and microbars were written either with IP-L or SU-8 50 photoresist using 3D Direct Laser Writing¹ (the Photonic Professional laser lithography system, Nanoscribe GmbH). After development, the microcarriers were coated with different thicknesses of Ni/Ti bilayers using Physical Vapor Deposition (PVD). Right before experiments, all microcarriers and microbars were immersed in a PLL-g-PEG solution for at least two hours. Fig. S1(a)† shows the fabrication protocol. As described in the manuscript, the single point contact of the helical shape does not provide strong attachment to the surface and therefore structures do not stay standing on the substrate during development. We addressed this problem by designing microcarriers with rings (see Fig. S1(b) and (c)†). The new design showed excellent performance of lateral motion with minimized wobbling at low rotational frequency (Fig. S1(d)†).

Experimental setup

The detailed information about the electromagnetic manipulation system can be found in our previous work.^31,33 The system consists of six stationary electromagnetic coils and is capable of producing magnetic fields up to 10 mT and at frequencies up to 200 Hz. Microcarriers and microbars are immersed in deionized (DI) water inside a plastic reservoir (35 mm × 35 mm × 3 mm), which is always placed at the centre of the magnetic coils. Using this setup, the motion of the carriers can be controlled in 6-DOF (x, y, z, pitch, yaw, roll).

Acknowledgements

We thank Dr Roel Pieters and Soichiro Tottori for insightful discussions on this work and the FIRST lab of ETH Zurich for technical support. This paper is funded by China Scholarship Council, National Natural Science Foundation of China (60874017, 71371092), and the European Research Council Advanced Grant “Microrobotics and Nanomedicine (BOTMED)”.

References

1. P. Y. Chiou, A. T. Ohta and M. C. Wu, Nature, 2005, 436(7049), 370–372.
2. J. D. Desai, A. Pillarisetti and A. D. Brooks, Annu. Rev. Biomed. Eng., 2007, 9, 35–53.
3. K. Dholakia and T. Cizmar, Nat. Photonics, 2011, 5, 335–342.
4. E. W. H. Jager, O. Inganas and I. Lundstrom, Science, 2000, 288, 2335–2338.
5. B. J. Nelson, I. K. Kaliakatsos and J. J. Abbott, Annu. Rev. Biomed. Eng., 2010, 12, 55–85.
6. T. Petit, L. Zhang, K. E. Peyer, B. E. Kratochvil and B. J. Nelson, Nano Lett., 2012, 12, 156–160.
7. R. Fernandes and D. H. Gracias, Mater. Today, 2009, 12, 14–20.
8. E. Gultepe, J. S. Randhawa, S. Kadam, S. Yamanaka, F. M. Selaru, E. J. Shin, A. N. Kalloo and D. H. Gracias, Adv. Mater., 2013, 25, 514.
9. W. Xi, A. A. Solovev, A. N. Ananth, D. H. Gracias, S. Sanchez and O. G. Schmidt, Nanoscale, 2013, 5, 1294.
10. S. Fusco, M. S. Sakar, S. Kennedy, C. Peters, R. Bottani, F. Starsich, A. Mao, G. A. Sotiriou, S. Pane, S. E. Pratsinis, D. Mooney and B. J. Nelson, Adv. Mater., 2014, 26, 952–957.
11. E. B. Steager, M. S. Sakar, D. H. Kim, V. Kumar, G. J. Pappas and M. J. Kim, J. Micromech. Microeng., 2011, 21, 035001.
12. R. Fernandes, M. Zuniga, F. R. Sassine, M. Karakoy and D. H. Gracias, Small, 2011, 7, 588–592.
13. V. Chan, H. H. Asada and R. Bashir, Lab Chip, 2013 10.1039/c3lc50989c.
14. W. Wang, T.-Y. Chiang, D. Velegol and T. E. Mallouk, J. Am. Chem. Soc., 2013, 135, 10557–10565.
15. J. Palacci, S. Sacanna, A. Vatchinsky, P. M. Chaikin and D. J. Pine, J. Am. Chem. Soc., 2013, 135, 15978–15981.
16. J. Wang, Lab Chip, 2012, 12, 1944–1950.
17. D. Patra, S. Sengupta, D. Wentao, H. Zhang, R. Pavlick and A. Sen, Nanoscale, 2013, 5, 1273.
18. A. A. Solovev, S. Sanchez and O. G. Schmidt, Nanoscale, 2013, 5, 1284.
19. P. Fischer and A. Ghosh, Nanoscale, 2011, 3, 557–563.
20. K. E. Peyer, L. Zhang and B. J. Nelson, Nanoscale, 2013, 5, 1259.
21. D. R. Frutiger, K. Vollmers, B. E. Kratochvil and B. J. Nelson, Int. J. Robot. Res., 2010, 29, 613–636.
22. E. B. Steager, M. S. Sakar, C. Magee, M. Kennedy, A. Cowley and V. Kumar, Int. J. Robot. Res., 2013, 32, 346.
23. S. Floyd, C. Pawashe and M. Sitti, IEEE Transactions on Robotics, 2009, 25, 1332–1342.
24. T. G. Leong, C. L. Randall, B. R. Benson, N. Bassik, G. M. Stern and D. H. Gracias, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 703–708.
25. M. Hagiwara, T. Kawahara, Y. Yamanishi, T. Masuda, L. Feng and F. Arai, Lab Chip, 2011, 11, 2049–2054.
26. W. Hu, K. S. Ishii, Q. Fan and A. T. Ohta, Lab Chip, 2012, 12, 3821–3826.
27. H.-W. Tung, K. E. Peyer, D. F. Sargent and B. J. Nelson, Appl. Phys. Lett., 2013, 103, 114101.
28. E. M. Purcell, Am. J. Phys., 1977, 45, 3.
29. K. E. Peyer, S. Tottori, F. Qiu, L. Zhang and B. J. Nelson, Chem.–Eur. J., 2013, 19, 28–38.
30. J. Abbott, K. E. Peyer, M. C. Lagomarsino, L. Zhang, L. X. Dong, I. K. Kaliakatsos and B. J. Nelson, Int. J. Robot. Res., 2009, 28, 1434–1447.
31. L. Zhang, J. J. Abbott, L. X. Dong, B. E. Kratochvil, D. J. Bell and B. J. Nelson, Appl. Phys. Lett., 2009, 94, 064107.
32. A. Ghosh and P. Fischer, Nano Lett., 2009, 9, 2243–2245.
33. S. Tottori, L. Zhang, F. Qiu, K. K. Krawczyk, A. Franco-Obregon and B. J. Nelson, Adv. Mater., 2012, 24, 811–816.
34. J. Li, S. Sattayasamitsathit, R. Dong, W. Gao, R. Tam, X. Feng, S. Ai and J. Wang, Nanoscale, 2014 10.1039/c3nr04760a.
35. W. Gao, X. Feng, C. R. Kane, R. Tam, C. Hennessy and J. Wang, Nano Lett., 2014, 14, 305–310.
36. M. A. Zeeshan, R. Grisch, E. Pellicer, K. M. Sivaraman, K. E. Peyer, J. Sort, B. Ozkale, M. S. Sakar, B. J. Nelson and S. Pane, Small, 2014, 10, 1284–1288.
37. M. Suter, L. Zhang, E. C. Siringil, C. Peters, T. Luhmann, O. Ergeneman, K. E. Peyer, B. J. Nelson and C. Hierold, Biomed. Microdevices, 2013, 15, 997–1003.
38. K. E. Peyer, L. Zhang and B. J. Nelson, Appl. Phys. Lett., 2011, 99, 174101.
39. L. Zhang, K. E. Peyer and B. J. Nelson, Lab Chip, 2010, 10, 2203–2215.
40. S. Cooper and M. W. Denny, FEMS Microbiol. Lett., 1997, 148, 227–231.
41. S. Kim, F. Qiu, S. Kim, A. Ghanbari, C. Moon, L. Zhang, B. J. Nelson and H. Choi, Adv. Mater., 2013, 25, 5863–5868.

---

Footnote

† Electronic supplementary information (ESI) available: Additional information is available on materials and methods, experimental setup, analytical drag model and three micromanipulation movies recorded in real time. See DOI: 10.1039/c4ra02260b

---