DOI:
10.1039/C4RA02053G
(Paper)
RSC Adv., 2014,
4, 24286-24294
Structural and electronic properties of tungsten nanoclusters by DFT and basin-hopping calculations†
Received
9th March 2014
, Accepted 22nd May 2014
First published on 23rd May 2014
Abstract
The structural and electronic properties of small tungsten nanoclusters Wn (n = 2–16) were investigated by density functional theory (DFT) calculations. For the W nanocluster, the lowest-energy structures were first obtained by the basin-hopping method (BH) with the tight-binding many-body potential for a bulk tungsten material. These structures were further optimized by DFT calculations in order to find better parameters of the tight-binding (TB) and Finnis–Sinclair (FS) potential appropriate for W nanoclusters. The values of binding energy and second-order energy difference reveal that the structure W11 has a higher stability than those of other sizes. The vertical ionization potential (VIP), adiabatic electron affinity (AEA) and HOMO–LUMO gap are also discussed for W nanoclusters of different sizes. In addition, large size nanoclusters Wn (n = 30–120) are obtained by the BH method, and a comparison of the structural properties determined by TB and FS potentials are represented with Honeycutt–Andersen index analysis.
1. Introduction
The refractory metal tungsten (W) has excellent physical and chemical properties, such as high melting point (about 3420 °C), high density (19.3 g cm−3), high strength and excellent creep resistance at room and elevated temperatures, high electron emissivity and low vapor pressure.1 The applications of W have now covered various fields such as lighting, electronics, catalysis, high-temperature technology, medicine, aviation, military uses, and so on.2–4 W nanostructures, due to their large surface–volume ratio, quantum size effects and surface effects exhibit some different thermal, mechanical, electronic and chemical properties when compared to their bulk counterpart, and thus exhibit high potential applications as nano-interconnectors, high-performance catalysts, and nano-electron-emitters. In the last few decades, W nanoclusters with diameters of 10–100 nm have been produced by several methods,5 such as salt assisted combustion reaction (SACR),6 plasma processing technique (PPT),7 electrical explosion of wires,8 high energy ball-milling,9 and physical vapor deposition (PVD).10 Moreover, W nanoclusters with sizes below 10 nm, have also been synthesized by the different methods of molten salt-assisted self-propagating high-temperature synthesis (SHS),11 metal-doping,12 gas-phase combustion synthesis,13 solvothermal decomposition method,14 and other chemical reduction processes.15,16 However, due to some technical problems in experiments, it is quite difficult to confirm their structures and electronic properties.
It has been well-demonstrated that theoretical calculations and simulations are a powerful alternative to the direct experiments for investigating the nanoclusters, and have been widely applied to explain and/or forecast the size-dependent properties. The structures and electronic properties of Wn (n = 2, 3) clusters have been studied using density functional theory (DFT) calculation by Wu et al.17 Their results have also been compared with those of experiment.18 Furthermore, Zhang et al.19 investigated the geometry and electronic structures of anionic and neutral states of Wn (n = 2–4) clusters. They found the stable geometry for each size cluster, and then analyzed the frequency results, binding energy and photoelectron spectra (PES) of the clusters.20 Zhang's group21 also investigated the adsorption properties of N2 molecules on neutral, anionic, and cationic Wn (n = 2–5) clusters using DFT at B3LYP and PW91 levels. They found by electronic and frequency analysis19,22 that the bond length and frequency influences the adsorptive ability between the W cluster and the N2 molecule.23–25
Since structural change is always an important factor influencing the catalytic and electronic properties of materials, this study performs DFT calculations to investigate the structural and electronic properties of Wn (n = 2–16) nanoclusters. To understand the electronic structures of tungsten nanoclusters, the stable geometry of Wn (n = 2–16) nanoclusters26 must also be found. Therefore, we first employ the molecular statics (MS) of big-bang (BB) and basin-hopping (BH) algorithms to find the most stable configuration of Wn (n = 2–16) nanoclusters. In order to obtain more accurate structures, the Dmol3 quantum chemical package was used to optimize these product configurations found in MS simulation. The detailed procedures of the lowest-energy structure search are introduced in the simulation model section. Finally, the binding energy, second-order energy difference, HOMO–LUMO gap, ionization potential and electronic affinity of tungsten nanoclusters Wn (n = 2–16) were investigated by DFT calculations.
2. Simulation model
2.1 Small Wn (n = 2–16) nanoclusters modeled by DFT
The size effect on the structural stability and electronic properties of the W nanoclusters was investigated by DFT. Above all, the most important procedure is to first obtain the energetically favorable configuration of the tungsten nanocluster, i.e., the lowest-energy structures of W nanoclusters (global minima structures), before determining the nanocluster properties. For this purpose, two stochastic methods, i.e., the big bang (BB)27,28 and basin-hopping (BH)29,30 algorithms, were first carried out by using tight-binding31,32 and Finnis–Sinclair (FS) potential.33 In the traditional BH method, a conjugate gradient method was used to reach the local minimum where a new geometry is generated. In our BH method, the conjugate gradient method was replaced by the limited memory BFGS method (LBFGS),34 which can be used to simulate a system consisting of a great number of atoms and whose calculation rate in the BH method is faster than that of the conjugate gradient method.
The interaction between two W atoms depends not only on the distance between those atoms, but also on their local environment. The algorithm for computing this potential is relatively simple compared to other many body potentials. This model commences by summing the band energy, which is characterized by the second moment of the d-band density of state (DOS), and a pairwise potential energy of the Born–Mayer type. The TB interatomic energy of atom i is thus expressed as follows:31
| |
 | (1) |
where
ξ is an effective hopping integral,
rij is the distance between atom
i and
j, and
r0 is the first-neighbor distance. The parameters
A,
p,
q, and
ξ for bulk W material are listed in
Table 1.
35 In addition, the FS potential are also used to find the initial structures of W nanocluster. The potential formula is given by:
| |
 | (2) |
where the
UN and
UNp stand for N-body and repulsive terms, respectively. The
rij is the inter atomic distance between atom
i and
j. The density is given by
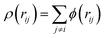
, and the density function
ϕ and cut-off distance are described as follows:
| |
 | (3) |
where the parameter
d are set depend on lattice constant. Further, the repulsive part is given by:
| |
 | (4) |
where the parameter of
c0,
c1, and
c2 are the fitting parameters,
c is a cut-off parameter assumed to lie between the second and the third neighbor atoms.
Table 1 Parameters used in the bulk tight-binding potential
| Parameters |
A (eV) |
ζ (eV) |
p |
q |
r0 (Å) |
| Wbulk |
0.249 |
3.2055 |
10.3715 |
1.9916 |
2.741 |
To find the global minima structure, one hundred lowest-energy structures for each Wn (n = 2–16) nanocluster, were obtained by BB and BH method with TB potential and FS potential. Furthermore, these structures were optimized by DMol3 package36,37 with DFT simulation in order to determine more accurate structures. The DMol3 package sets employed density functional semi-core pseudopotentials (DSPP) calculations with double numerical basis sets polarization p-functional (DNP), and the generalized gradient approximation (GGA)38 by Perdew and Wang parameterization (PW91)39,40 correction. Spin-polarization was considered in our calculation. The self-consistent field (SCF) tolerance and integration accuracy were all set to “fine” with high accuracy of 10−6 au for energy convergence. After the W clusters were obtained from BB and BH methods, they were fully optimized by means of the DMol3 package to obtain the three lowest-energy structures of Wn (n = 2–16).
2.2 Large Wn (n = 30–120) nanoclusters modeled by the Honeycutt–Andersen (HA) index
Large tungsten nanoclusters were also considered in this simulation, with the FS and TB potentials applied to analyze the structural properties. A useful assessment of local configuration is given by the method of Honeycutt–Andersen (HA) index analysis.41 The sequence of four integers (i, j, k, l) and the concept of radial distribution function (RDF) for finding the near-neighbor atoms were employed to define the different configuration distribution of local structures. The first integer of this index is useful in judging whether or not the root pair of two random atoms is bonded; it is 1 when bonding exists, 2 if not. The second integer represents the number of near-neighbor atoms shared in common by the root pair; the third integer stands for the number of near-neighbor bonds between the shared neighbors; the fourth integer is used to distinguish different structures which share the same preceding three numbers. According the HA index analysis, body centered cubic (BCC) structures are described by 1441, and face centered cubic (FCC) by 1421. In addition, the index 1422 consists of 50% FCC and 50% hexagonal close packed (HCP) structures.
3. Results and discussion
3.1 Small Wn (n = 2–16) nanocluster and DFT calculation
To verify the reliability of our DFT model, Table 2 lists the calculated lattice constant and cohesive energy compared with experimental values of tungsten BCC, FCC, and HCP lattices.42,43 The binding energy by BPW91 correction in a previous study is also presented.44 We calculate the properties of W bulk material by BPW91 and PW91, but the binding is closer to the bulk when using the PW91 function. Moreover, the lattice constant is 3.165 nm, also in near agreement with the experiment values of 3.16 nm and 3.25 nm.45,46 We employ the two functional of PW91 and BPW91 to calculate the bond length, frequency, and dissociation energy of the tungsten dimer cluster, shown in Table 3, with calculation setups of PW91/DNP/DSPP and BPW91/DNP/DSPP. Also shown are results of previous studies, both experimental and theoretical. The bond length results are different by changing initial bond length, and the frequency and dissociation energy of ω = 249.7 and 387.5 cm−1 and Ed = 5.34 and 5.49 eV are very close to the experimental values.47,48 According to this preliminary test calculation on the W dimer by using different functional methods, PW91/DNP/DSPP appears more accurate, and is used to study the remaining cases.
Table 2 The results of binding energy using BPW91 and PW91 functional for bulk tungsten materials
| |
|
EXP |
PW91/DNP/DSPP |
BPW91/DNP/DSPP |
| Ref. 42. Ref. 43. Ref. 45. Ref. 46. |
| WFCC |
Cohesive energy |
8.33–8.45a |
8.36 |
|
| WHCP |
Cohesive energy |
8.33b |
8.19 |
|
| WBCC |
Cohesive energy |
8.9a |
8.9 |
8.674 |
| Lattice constant |
3.16,c 3.25d |
3.165 |
3.165 |
Table 3 The results of bonding, frequency, and dissociative energy using BPW91 and PW91 functional for tungsten dimer
| |
Method |
R (Å) |
ω (cm−1) |
Ed (eV) |
| Ref. 44. Ref. 47. Ref. 48. This work. |
| W2 |
PW91/DNP/DSPP |
2.05d |
310.5d |
5.44d |
| BPW91/DNP/DSPP |
2.053a |
376a |
5.22a |
| Expt. |
|
337b |
5 ± 1c |
After optimization by DFT, the three lowest-energy isomers for each W nanocluster are presented in Fig. 1. The energy of the lowest-energy isomer was used as the reference value for the W nanoclusters of the same size. The values in the parentheses are energy differences between the isomers and the lowest-energy structure. The binding energies and average bond lengths of the lowest-energy Wn (n = 2–16) nanoclusters were calculated to understand the stability and structural properties of W nanoclusters, these results are listed in Table 4. The binding energy per atom Eb can be determined by the following equation:
| | |
Eb = [ETol − n × Eatom]/n
| (5) |
where
ETol is the total electronic energy of the W nanocluster with atom number
n, and
Eatom is the electronic energy of an isolated W atom. In
Fig. 2, the binding energy of the W nanocluster increases with the enhancement of the nanocluster size, demonstrating that a larger nanocluster will have higher thermal stability. This can be attributed to the fact that the average bond lengths of W atoms will increase for a larger W nanocluster, which leads to the significant overlap of 6p orbital and the increase in the binding energy. For
n = 3 to 8, the binding energy of 2D ground-state nanocluster (2D structures are shown in the ESI
†) displays a sharp increase from 3.74 to 4.65 eV, while for
n = 2 to 16, the binding energy of 3D ground-state nanocluster shows a relatively slight increase from 2.67 to 6.03 eV. The binding energy of the largest W nanocluster, W
16, has reached 68% of the binding energy of bulk W material. The variation of average bond length seems to be sensitive to the nanocluster with average W–W bond lengths for
n = 2 to 16 being between 2.65 and 2.61 Å, about 10–14% shorter than that in bulk W material.
49
 |
| | Fig. 1 Wn (n = 2–16) ground-state geometries with isomer structures and energies relative to the energies of their ground states. The unit of energy is eV. | |
Table 4 The average binding energy of Wn (n = 2–16) ground-state geometries by the sets of PW91/DNP/DSPP and BPW91/DNP/DSPP
| Cluster |
Rav (Å) |
Eb per atom (eV) |
| BP |
PW91 |
| W2 |
2.051 |
2.65 |
2.67 |
| W3 |
2.324 |
3.60 |
3.70 |
| W4 |
2.404 |
4.07 |
4.19 |
| W5 |
2.467 |
4.57 |
4.70 |
| W6 |
2.479 |
4.88 |
5.02 |
| W7 |
2.508 |
5.08 |
5.22 |
| W8 |
2.510 |
5.29 |
5.41 |
| W9 |
2.530 |
5.38 |
5.52 |
| W10 |
2.541 |
5.45 |
5.61 |
| W11 |
2.545 |
5.57 |
5.73 |
| W12 |
2.563 |
5.62 |
5.78 |
| W13 |
2.561 |
5.70 |
5.84 |
| W14 |
2.580 |
5.75 |
5.90 |
| W15 |
2.583 |
5.79 |
5.96 |
| W16 |
2.590 |
5.85 |
6.03 |
 |
| | Fig. 2 The binding energy (eV) and average bond length of the 2D and 3D ground-state structures as a function of number of W atoms. | |
The second-order energy difference (Δ2E) is also discussed in the present study because it is a useful parameter to examine the relative stability of the Wn nanocluster with respect to Wn+1 and Wn−1. This parameter is defined as eqn (6).50
| | |
Δ2E(Wn) = [E(Wn−1) + E(Wn+1) − 2E(Wn)]
| (6) |
where
E(W
n)is the total energy of W nanocluster with
n atoms.
Fig. 3 shows the profile of Δ
2E (W
n) as a function of the atom number
n. For
n = 11, a peak with a positive Δ
2E value indicates that the W
11 displays relatively higher thermal stability than W
10 and W
12. The energy of the first isomer of W
11 is found to be the closest to the ground-state and all energy differences are smaller than 1 eV. For the ground-state geometry of W
12, it is capped pentagon bipyramidal.
51–53 Note that the ground-state geometry of W
13 is not perfectly icosahedral, unlike previous configurations found for W
13. It can be seen that a surface atom sticks slightly out from the cluster surface in
Fig. 1. In fact, we also can obtain by using BB and BH method with tight-binding potential parameters. However, the geometry of C1 symmetry is more stable configuration after DFT optimization in our calculation progress.
 |
| | Fig. 3 The plot of Δ2E for different number of W atoms. | |
Fig. 4 shows the profile of HOMO–LUMO gap50,54 for the W nanocluster with different sizes. It can be found that almost all gaps of Wn (n = 2–16) were larger than 0.15 eV. W2, W3, and W4 have larger gaps than 0.5 eV, indicating the higher chemical inertness of these nanoclusters. A drop in the HOMO–LUMO gap was found when the size of W nanocluster became larger than 5. These significant orbital overlaps also cause a considerable increase in the binding energy when the size is larger than 5, and the slope of the binding energy curve gradually smoothens, as shown in Fig. 2. This result reflects the fact that more atomic orbitals overlap and the energy levels become gradually closer for a larger W nanocluster. Furthermore, the profile of the HOMO–LUMO gap presents a general odd–even oscillation, where the gap of nanoclusters with odd-numbered atoms is larger than neighboring even-numbered ones.
 |
| | Fig. 4 The plot of HOMO–LUMO gaps for different number of W atoms. | |
In order to investigate the electron donating and accepting ability of W nanoclusters with different sizes, both vertical ionization potential (VIP) and adiabatic electron affinity (AEA)53,55 were calculated. The VIP is defined as the minimum required energy to remove an electron from the W nanocluster at the ground state, a value that can be determined by the energy difference between the neutral and cation species with the same geometry at the ground state. The VIP value can be represented by the following relation:
| | |
VIP = W(E+) − Wopt(E0)
| (7) |
where W(
E+) and W
opt(
E0) are the electronic energies of the cation and neutral nanoclusters with the same geometry at the ground state, respectively. The VIP profile as a function of W atom number is shown in
Fig. 5. The variation of VIP value with the W atom number is insignificant and varies near 5 eV.
 |
| | Fig. 5 The vertical ionization potential (VIP) shown as a function of number of W atoms. | |
The AEA is defined as the energy change after the W nanocluster attains an electron. This parameter can be estimated by the energy change between the neutral and the anion W nanoclusters with the same geometries at the ground state. The AEA of the W nanoclusters are calculated by the following relationship,
| | |
AEA = Wopt(E0) − W(E−)
| (8) |
where W(
E−) is the energy of anion nanocluster. If AEA is positive, the anion nanocluster is more stable than the neutral one. The AEA profile as a function of W atom number is shown in
Fig. 6, suggesting that the AEA values of W
n (
n = 2–16) were all positive. The AEA value dramatically increases with the increase in W nanocluster size, implying that a electronic transfer of chemical reaction from the adsorbed molecule to W nanocluster is more preferable for large size nanocluster.
 |
| | Fig. 6 The adiabatic electron affinities (AEAs) shown as a function of number of W atoms. | |
It is well-known that the distribution of valence electrons of a W atom is located in the s and d orbital, which is filled in 5d46s2. When W atoms gather together as a cluster, their itinerant electrons are affected by the interaction between W atoms and may lead to the excitation of itinerant electrons to the higher energy level orbital (i.e., 6p orbital), causing an electronic disturbance in the valence-band. Therefore, the Mulliken population analysis of Wn (n = 2–16) nanoclusters was calculated to investigate the valence electronic structures listed and showed in Table 5 and Fig. 7 for the electronic charges in 5d, 6s, 6p and the sum. The charge is between 4.44 and 4.56 in the 5d orbital and 1.17 to 1.5 in the 6s orbital. From Table 5, it can be observed that the charge distribution for all cases have partially filled the 5d, 6s and 6p orbitals. However, most of the valence electrons are located in the 5d and 6s orbitals. The charge distribution of n = 15 and 16 shows a larger electronic transfer in 6s compared to other nanoclusters. This result may explain why their AEAs have the lowest value. In addition, the electronic distribution of the 6p orbital for small size nanoclusters is lower than that for other nanoclusters. This is probably caused by the higher band gap energy.
Table 5 The Wn (n = 2–16) nanocluster charges for 5d, 6s, and 6p orbitals by population analysis
| Atom |
Orbit |
Charge |
Sum |
| W2 |
5d |
4.901 |
6.008 |
| 6s |
1.503 |
| 6p |
0.054 |
| W3 |
5d |
4.561 |
6.002 |
| 6s |
1.264 |
| 6p |
0.177 |
| W4 |
5d |
4.442 |
6.0 |
| 6s |
1.362 |
| 6p |
0.197 |
| W5 |
5d |
4.533 |
5.995 |
| 6s |
1.237 |
| 6p |
0.226 |
| W6 |
5d |
4.539 |
5.994 |
| 6s |
1.212 |
| 6p |
0.244 |
| W7 |
5d |
4.478 |
5.992 |
| 6s |
1.215 |
| 6p |
0.298 |
| W8 |
5d |
4.497 |
5.99 |
| 6s |
1.226 |
| 6p |
0.268 |
| W9 |
5d |
4.471 |
5.99 |
| 6s |
1.201 |
| 6p |
0.317 |
| W10 |
5d |
4.521 |
5.988 |
| 6s |
1.186 |
| 6p |
0.280 |
| W11 |
5d |
4.499 |
5.987 |
| 6s |
1.189 |
| 6p |
0.30 |
| W12 |
5d |
4.483 |
5.987 |
| 6s |
1.193 |
| 6p |
0.311 |
| W13 |
5d |
4.488 |
5.986 |
| 6s |
1.188 |
| 6p |
0.311 |
| W14 |
5d |
4.498 |
5.988 |
| 6s |
1.2 |
| 6p |
0.29 |
| W15 |
5d |
4.479 |
5.986 |
| 6s |
1.178 |
| 6p |
0.329 |
| W16 |
5d |
4.464 |
5.985 |
| 6s |
1.184 |
| 6p |
0.337 |
 |
| | Fig. 7 The charge distribution for 5d, 6s, and 6p orbitals. | |
3.2 Large Wn (n = 30–120) nanoclusters and HA index analysis
Large nanoclusters are also considered by the progress of searching global minima structures. Previous studies have indicated that the TB potential is most suitable to describe FCC and HCP structures,31 and FS is preferable for BCC configurations. However, until now, the studies of W nanoclusters which use the FS potential are still lack. We employ both TB and FS potentials to find the lowest-energy structures by the BH method. The HA index analysis is represented in Fig. 8. The red, pink, green, and orange lines represent the fractions of BCC, FCC, FCC–HCP phases, and amorphous structures, respectively. There are different phase transitions which can be observed in three regions. At sizes smaller than 45 atoms, the crystal phases are not ordered significantly. At sizes larger than W45, the fraction of 1422 HA index increases significantly. At sizes larger than about 80 atoms, the fraction of 1421 and 1422 HA index configurations rise with a concomitant drop in amorphous levels. Moreover, the fraction of BCC phase does not follow any specific tendency while size increases. In addition, the lowest-energy structures for large size nanoclusters found using FS potentials are represented in Fig. 9. Clearly, the fraction of BCC phase is higher than other crystal types for nanoclusters ranging from sizes of 30 to 120. It can be observe that the lowest-energy structures at the size of 60, and 116 possess higher properties of BCC phase, these structures are shown in Fig. 10(a)–(d). The cubic structures are easily associated with BCC crystal for W60, as shown in panel (a). However, it is not similar to the structure which found by TB potential in Fig. 10(b). In the case of W116, FS-used structure also represents a higher fraction of BCC phase than TB-used structure, as shown in Fig. 10(c) and (d). In the FS-used abd TB-used structure distribution, the 1422 HA index peak can be observed at the 54–56 atom range. The lowest-energy structures of W54 are found by both the FS and TB potentials are the same, as shown in Fig. 11(a). We analyze the structure of W54 by HA index, the amorphous structures can also be calculated and excluded for reveal the configuration of different phases. In general, the amorphous phase fraction is higher in the large nanoclusters because the surface atoms are also calculated when all atoms are considered in the HA index analysis. In Fig. 11(b), the pair fractions are shown, all the pairs of atoms which are included in the crystal structures in W54 nanoclusters. The yellow atoms are the i atom and j atom which are the basic pair; the standard 1422 arrangement is shown by the blue atoms, and the other green atoms are neighbor atoms of the i–j pair in calculations. From W54, the different results between FS and TB are rising depend on the increase of size (the other sizes of W nanoclusters are shown in the ESI†).
 |
| | Fig. 8 The distribution of structures found using TB potential for large size nanoclusters Wn (n = 30–120). The red, pink, green, and orange lines are the fractions of BCC, FCC, FCC–HCP phase, and amorphous structures, respectively. | |
 |
| | Fig. 9 The distribution of structures found using FS potential for large size nanoclusters Wn (n = 30–120). The red, pink, green, and orange lines are the fractions of BCC, FCC, FCC–HCP phase, and amorphous structures, respectively. | |
 |
| | Fig. 10 W60 found by BH method with (a) FS and (b) TB potentials; W116 structures calculated by BH method with (c) FS and (b) TB potentials. | |
 |
| | Fig. 11 (a) W54 found by both FS and TB potential methods; (b) the partial structure of the W54 nanoclusters. | |
4. Conclusions
We use the DFT method to investigate the structural and electronic properties of small tungsten nanoclusters Wn (n = 2–16). The global minima structures using the TB and FS potential for W nanoclusters are found. The geometry of Wn (n = 2–16) nanoclusters with stable energies are determined by using (BB) and basin-hopping (BH) methods. The DMol3 package is employed to find the configuration of nanoclusters with lowest energy. The results of calculating binding energy demonstrate that W11 has the highest stability. The average bond length seems to be insensitive to the nanoclusters size for Wn (n = 2–16), but are shorter than that in bulk W material. In addition, a peak with a positive Δ2E value indicates that the nanocluster for n = 11 is more stable than nanoclusters close in size. Furthermore, the n = 2 and 14 nanoclusters are found have the highest and lowest VIP values, respectively. Our AEA results show that Wn (n = 2–16) are all positive and the value rises with increasing nanocluster size. According to these AEA results, W15 has better properties for electronic transfer. In our large size nanoclusters study, Wn (n = 30–120) nanoclusters were found by TB and FS potential. A higher fraction of BCC phase is represented when the FS potential was used, and high fractions of FCC and HCP phase are shown when we employed TB potential. Interestingly, both TB and FS potentials are used in the W54 size nanocluster, and the same structure is found. This structure is considered to be of a special size which possesses a significant fraction of HCP phase. From the HA index analysis, the FS potential indeed reflect the cubic structures of W materials than the TB potential. In this study, we conclude that the W nanoclusters are not must BCC or FCC and HCP configurations in small size. Because significant computation time is required for DFT calculations of large W nanoclusters, larger tungsten clusters will be topics of future study.
Acknowledgements
The authors would like to acknowledge the (1) National Science Council, Republic of China, under Grant no. NSC 101-2628-E-110-003-MY3 for the financial support, (2) National Center for High-performance Computing, Taiwan, for the use of computer time, (3) National Center for Theoretical Sciences, Taiwan.
References
- E. Lassner and W. D. Schubert, Tungsten: Properties, Chemistry, Technology of the Element, Alloys, and Chemical Compounds, New York, 1998 Search PubMed.
- W. T. Wallace and R. L. Whetten, J. Am. Chem. Soc., 2002, 124, 7499–7505 CrossRef CAS PubMed.
- H. Y. Kim, D. H. Kim, J. H. Ryu and H. M. Lee, J. Phys. Chem. C, 2009, 113, 15559–15564 CAS.
- J. Gustafson, R. Westerstrom, O. Balmes, A. Resta, R. van Rijn, X. Torrelles, C. T. Herbschleb, J. W. M. Frenken and E. Lundgren, J. Phys. Chem. C, 2010, 114, 4580–4583 CAS.
- H. Henry Hwu, D. Brian Polizzotti and G. Jingguang Chen, J. Phys. Chem. B, 2001, 105, 10045–10053 Search PubMed.
- J. B. Benziger, E. I. Ko and R. J. Madix, J. Catal., 1978, 54, 514 CrossRef.
- C. M. Friend, P. A. Stevens, J. G. Serafin, E. K. Baldwin and R. J. Madix, J. Chem. Phys., 1987, 87, 1847 CrossRef CAS PubMed.
- P. A. Stevens, C. M. Friend and R. J. Madix, Surf. Sci., 1988, 205, 187 CrossRef CAS.
- B. Fruhberger and J. G. Chen, J. Am. Chem. Soc., 1996, 118, 11599 CrossRef.
- B. Fruhberger and J. G. Chen, Surf. Sci., 1995, 38, 342 Search PubMed.
- H. H. Nersisyan, J. H. Lee and C. W. Won, Combust. Flame, 2005, 142, 241 CrossRef CAS PubMed.
- R. K. Barik, A. Bera, A. K. Tanwar, I. K. Baek, S. H. Min, O. J. Kwon, W. S. Lee and G.-S. Park, Int. J. Refract. Met. Hard Mater., 2013, 38, 60–66 CrossRef CAS PubMed.
- R. L. Axelbaum, J. I. Huertas, C. R. Lottles, S. Hariprasad and S. M. L. Sastry, Mater. Manuf. Processes, 1996, 11, 1043 CrossRef CAS.
- P. K. Sahoo, S. S. K. Kamal, M. Premkumar, T. Jagadeesh Kumar, B. Sreedhar, A. K. Singh, S. K. Srivastava and K. Chandra Sekhar, Int. J. Refract. Met. Hard Mater., 2009, 27, 784 CrossRef CAS PubMed.
- Y. Gao, J. Zhao, Y. Zhu, S. Ma, X. Su and Z. Wang, Mater. Lett., 2006, 60, 3903 CrossRef CAS PubMed.
- N. J. Welham, J. Mater. Res., 1999, 14, 619 CrossRef CAS.
- Z. J. Wu, Chem. Phys. Lett., 2003, 370, 510 CrossRef CAS.
- H. Weidele, D. Kreisle and E. Recknagel, et al., Chem. Phys. Lett., 1995, 237, 425 CrossRef CAS.
- X. R. Zhang, X. L. Ding, B. Dai and J. L. Yang, J. Mol. Struct.: THEOCHEM, 2005, 757, 113 CrossRef CAS PubMed.
- H. Weidele, D. Kreisle, E. Recknagel, G. Schulze Icking-Konert, H. Handschuh, G. Ganteför and W. Eberhardt, Chem. Phys. Lett., 1995, 237, 425 CrossRef CAS.
- X. Zhang, J. Mol. Struct.: THEOCHEM, 2008, 867, 17–21 CrossRef CAS PubMed.
- X. Zhang, X. Ding and J. Yang, Int. J. Mod. Phys. B, 2005, 19, 2427 CrossRef CAS.
- H. Weidele, D. Kreisle, E. Recknagel, G. S. Icking-Konert, H. Handschuh, G. Ganteför and W. Eberhardt, Chem. Phys. Lett., 1995, 237, 425 CrossRef CAS.
- D. T. Birtwistle and A. Herzenberg, Phys. Rev. B: Solid State, 1971, 4, 53 CrossRef CAS.
- T. Trickl, E. F. Cromwell, Y. T. Lee and A. H. Kung, J. Chem. Phys., 1989, 91, 600 CrossRef PubMed.
- W. Yamaguchi and J. Murakami, Chem. Phys., 2005, 316, 45 CrossRef CAS PubMed.
- K. A. Jackson, M. Horoi, I. Chaudhuri, T. Frauenheim and A. A. Shvartsburg, Phys. Rev. Lett., 2004, 93, 4 CrossRef.
- M. L. Yang, K. A. Jackson, C. Koehler, T. Frauenheim and J. Jellinek, J. Chem. Phys., 2006, 124, 024308 CrossRef PubMed.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- D. J. Wales and H. A. Scheraga, Science, 1999, 285, 1368–1372 CrossRef CAS.
- V. Rosato, M. Guillope and B. Legrand, Philos. Mag. A, 1989, 59, 321–336 CrossRef.
- F. Cleri and V. Rosato, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 22 CrossRef CAS.
- M. W. Finnis and J. E. Sinclair, Philos. Mag. A, 1984, 50, 45 CrossRef CAS.
- D. C. Liu and J. Nocedal, Mathematical programming, 1989, 45, 503–528 CrossRef.
- M. A. Karolewski, Radiat. Eff. Defects Solids, 2001, 153, 239–255 CrossRef CAS.
- B. Delley, J. Chem. Phys., 1990, 92, 508–517 CrossRef CAS PubMed.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764 CrossRef CAS PubMed.
- D. C. Langreth and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 21, 5469–5493 CrossRef.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800 CrossRef.
- J. D. Honeycutt and H. C. Andersen, J. Phys. Chem., 1987, 91, 4950–4963 CrossRef CAS.
- H. J. F. Jansen and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 561 CrossRef CAS.
- J. W. Davenport, M. Weinert and R. E. Watson, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 4876 CrossRef CAS.
- J. Du, X. Sun, D. Meng, P. Zhang and G. Jiang, J. Chem. Phys., 2009, 131, 044313 CrossRef PubMed.
- J. Michael Mehl and A. Dimitrios Papaconstantopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 4519 CrossRef.
- L. T. Kong, J. B. Liu, W. S. Lal and B. X. Liu, J. Alloys Compd., 2002, 337, 143–147 CrossRef CAS.
- Z. Hu, J. G. Dong, J. R. Lombardi and D. M. Lindsay, J. Chem. Phys., 1992, 97, 8811 CrossRef CAS PubMed.
- M. D. Morse, Chem. Rev., 1986, 86, 1049 CrossRef CAS.
- P. Villars, L. D. Calvert and W. B. Pearson, Acta Crystallogr., Sect. A: Found. Crystallogr., 1984, 40, C444 Search PubMed.
- M. X. Chen and X. H. Yan, J. Chem. Phys., 2008, 128, 174305 CrossRef PubMed.
- M. S. Lee, S. Chacko and D. G. Kanhere, J. Chem. Phys., 2005, 123, 164310 CrossRef PubMed.
- S. M. Ghazi, M. S. Lee and D. G. Kanhere, J. Chem. Phys., 2008, 128, 104701 CrossRef PubMed.
- W. Fa and J. M. Dong, J. Chem. Phys., 2006, 124, 114310 CrossRef PubMed.
- F. Chen and R. L. Johnston, Acta Mater., 2008, 56, 2374–2380 CrossRef CAS PubMed.
- P. K. Jain, Struct. Chem., 2005, 16, 421–426 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra02053g |
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here. 

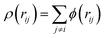 , and the density function ϕ and cut-off distance are described as follows:
, and the density function ϕ and cut-off distance are described as follows:












