Modulated T carbon-like carbon allotropes: an ab initio study
Da Li,
Fubo Tian,
Defang Duan,
Zhonglong Zhao,
Yunxian Liu,
Binhua Chu,
Xiaojing Sha,
Lu Wang,
Bingbing Liu and
Tian Cui*
State key Laboratory of Superhard Materials, College of Physics, Jilin University, Changchun 130012, P. R. China. E-mail: cuitian@jlu.edu.cn; Fax: +86-431-85168825; Tel: +86-431-85168825
First published on 2nd April 2014
Abstract
The structural stability, mechanical properties, and dynamical properties of T carbon-like structures were extensively studied by first-principles calculations using density functional theory. A novel modulated T carbon-like carbon allotrope (T-II carbon) is predicted by means of first principles calculations. This structure has 8 atoms in the unit cell, possesses the Pn![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, and can be derived by stacking up two T carbons together. T-II carbon is a semiconductor with band gap 0.88 eV and has a higher hardness (27 GPa) than that of T carbon (5.6 GPa). The calculations of ideal strength and the electron localization function indicate that T-II carbon has better ability to resist shear strain than T carbon.
m space group, and can be derived by stacking up two T carbons together. T-II carbon is a semiconductor with band gap 0.88 eV and has a higher hardness (27 GPa) than that of T carbon (5.6 GPa). The calculations of ideal strength and the electron localization function indicate that T-II carbon has better ability to resist shear strain than T carbon.
Introduction
Recently, the cold-compressed graphite phases have attached much more attention from theoretical and experimental workers.1–9 A series of cold compressed graphite phases have been predicted such as M carbon,1 bct-C4,2 W carbon,3 Z carbon (or Cco-C8),4,5 and so on. They have better mechanical properties. All the structures are composed of exclusively sp3-hybridized covalent bonds. The phase transformation mechanisms of cold-compressed graphite phases have been systematically studied.10–14 Some other sp3 bonded carbon allotropes have also been studied except cold-compressed graphite phases.15,16 Zhu et al. predicted three superdense carbon allotropes (hP3, tI12, and tP12) with significantly greater density and bigger hardness (87.6 GPa for hP3, 87.2 GPa for tI12, and 88.3 GPa for tP12).16 Pickard et al. predicted a sp3 bonded chiral framework structure with hexagonal symmetry.15 Two hypothetical cubic carbon cage-like structures (C6 and C20) with big bulk moduli (350 GPa) had also been predicted.17 Hu et al. predicted four cage-like cubic carbons (fcc-C32, bcc-C20, fcc-C12, and fcc-C10) which are composed by sp3-hybridization bonds or a mixed sp2- and sp3-hybridization bonds.18 Among the above mentioned carbon allotropes, carbon structures with cubic symmetry are of special interest due to high symmetrization of crystal structures and good mechanical properties, which are critical key for the formation and stability of superhard materials.17 Recently, a cubic T carbon with lower density (1.50 g cm−3) has been predicted by Sheng et al. using first-principles methods.19 It is obtained by substituting each atom in diamond with a carbon tetrahedron. The T carbon is a semiconductor with a direct band gap about 3.0 eV. And the density of T carbon is the smallest one among c-diamond, h-diamond, graphite, M carbon,1 and bct-C4.2 The large interspaces between carbon atoms along [100] and [110] directions of T carbon has been observed. The T carbon has been predicted to have better ability of hydrogen gas storage. Very recently, by inserting yne-bonding (triple bonding) into diamond and T carbon through a symmetry consideration, two T carbon-like structures (Y carbon and TY carbon) were obtained.20 They are energetically more stable than T carbon. They also were expected to have good hydrogen storage capacity because of the presence of carbon triple bonds and cavities in the structures. However, the bulk modulus of Y carbon and TY carbon are only 82.9 and 54.2 GPa, respectively, indicating very poor mechanical properties. The T carbon also has a low bulk modulus B (169 GPa) and shear modulus G (70 GPa) but an abnormal theoretical Vickers hardness (61.1 GPa).19 However, it is noteworthy that the discrepancy for the Vickers hardness of T carbon calculated by different empirical hardness models is very big.21 The hardness of T carbon calculated by Chen's hardness model is only 5.6 GPa. The ideal strength calculations were performed to confirm the real hardness of T carbon. It is found that the T carbon has big tensile strength (40.1 GPa) but a small shear strength (7.3 GPa).21 Therefore, it can be conjectured that the hardness of T carbon should not exceed 7.3 GPa. So Chen's hardness model has better results for the highly anisotropic structures.21 However, the hardness values of T carbon-like structures are smaller than that of diamond and c-BN. The poor mechanical properties make the value of potentially industrial application of T carbon-like structures reduce. Moreover, many fundamental physical properties of T carbon-like structures are still not well understood.In the present work, the structural stability, mechanical properties, and dynamical properties of T carbon-like structures are extensively studied by first-principles calculations based on density functional theory. We design a new cubic phase of elemental carbon with Pn![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry that has very intriguing physical properties. We name it as T-II carbon. The T-II carbon is structurally similar to T carbon. The mechanical properties of the T-II carbon have been studied. Furthermore, the original hardness of T-II carbon is revealed in this study. Electron localization function calculations indicate that T-II carbon has the same resistant mechanism for shear strain as that of T carbon. More compact arrangement of carbon atoms make T-II carbon has big hardness (27 GPa) than that of T carbon (5.6 GPa).
m symmetry that has very intriguing physical properties. We name it as T-II carbon. The T-II carbon is structurally similar to T carbon. The mechanical properties of the T-II carbon have been studied. Furthermore, the original hardness of T-II carbon is revealed in this study. Electron localization function calculations indicate that T-II carbon has the same resistant mechanism for shear strain as that of T carbon. More compact arrangement of carbon atoms make T-II carbon has big hardness (27 GPa) than that of T carbon (5.6 GPa).
Computational details
All calculations were performed with the density-functional theory22,23 implemented within the Vienna ab initio simulation package (VASP)24,25 with the projector augmented wave method.26 The 2s22p2 electrons were treated as valence electrons. In contrast to the early study, the generalized gradient approximation (GGA) with the Perdew Wang 91 (PW91) functional for the exchange correlation was employed.27 The tested plane–wave cutoff energy was taken as 1100 eV. The Monkhorst–Pack (MP)28 scheme was used to sample the Brillouin zone, and a tested mesh of 8 × 8 × 8 k-point sampling was used for the calculations. The geometries were optimized when the remanent Hellmann–Feynman forces on the ions are less than 0.01 eV Å−1. The details of convergence tests have been described elsewhere.6,29–31 The phonon spectra were calculated using the direct supercell method, performed by PHONON software.32Results and discussion
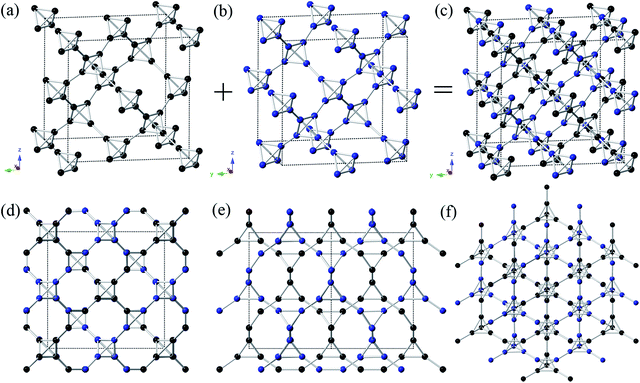
Inspired by the T carbon-like structures,19 in order to get good mechanical properties, we design a novel carbon allotrope, and name it as T-II carbon. The T-II carbon was derived by stacking up two T carbon structures together as shown in Fig. 1(a)–(c). The original T carbon was obtained by substituting each atom in diamond by carbon tetrahedron as shown in Fig. 1(a). Another one was got by moving 1/2 lattice vector of T carbon along the crystallographic a axis as shown in Fig. 1(b). Our study reveals a novel cubic structure with Pn![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry as depicted in Fig. 1(c)–(f). There are 8 atoms in the unit cell. The interspaces between carbon atoms in T-II carbon are smaller than that of T carbon. The density of T-II carbon is 2.955 g cm−3. At 0 GPa, the equilibrium lattice parameter is a = 3.78 Å. Within this structure, one inequivalent atom occupy the crystallographic 8e site in the unit cell, which is (0.14, 0.14, 0.14) position. The T-II carbon can be seen as the smallest unit of T carbon. Using the same method to Y carbon and TY carbon, we got two novel T carbon-like allotropes (Y-II carbon and TY-II carbon). They also had the Pn
m symmetry as depicted in Fig. 1(c)–(f). There are 8 atoms in the unit cell. The interspaces between carbon atoms in T-II carbon are smaller than that of T carbon. The density of T-II carbon is 2.955 g cm−3. At 0 GPa, the equilibrium lattice parameter is a = 3.78 Å. Within this structure, one inequivalent atom occupy the crystallographic 8e site in the unit cell, which is (0.14, 0.14, 0.14) position. The T-II carbon can be seen as the smallest unit of T carbon. Using the same method to Y carbon and TY carbon, we got two novel T carbon-like allotropes (Y-II carbon and TY-II carbon). They also had the Pn![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry. At 0 GPa, the equilibrium lattice parameters of Y-II carbon are a = 4.8302 Å. Two inequivalent atoms occupy the crystallographic 8e and 2a sites in the unit cell, which are (0.178, 0.178, 0.178) and (0, 0, 0) positions. The equilibrium lattice parameters of Y-II carbon are a = 7.7216 Å. One inequivalent atom occupy the crystallographic 8e site in the unit cell, which are (0.197, 0.197, 0.197) and (0.079, 0.079, 0.079) positions. The interspaces of T-II carbon, Y-II carbon and TY-II carbon also become smaller than that of their original structures. The equilibrium density of T-II carbon (2.955 g cm−3) is larger than that of T carbon (1.50 g cm−3) and smaller than that of diamond (3.49 g cm−3). The descending order of equilibrium densities is c-diamond (3.49 g cm−3) → M carbon (3.34 g cm−3) → bct-C4 carbon (3.32 g cm−3) → T-II carbon (2.955 g cm−3) → C6 carbon (2.85 g cm−3) → C20 carbon (2.81 g cm−3) → Y-II carbon (1.77 g cm−3) → T carbon (1.50 g cm−3) → TY-II carbon (1.05 g cm−3) → Y carbon (0.892 g cm−3) → TY carbon (0.52 g cm−3). It is well known that the densities of materials are critical for mechanical properties of materials.16 The T-II carbon has the bigger density among T carbon-like structures. So we can expect that the T-II carbon has better mechanical properties than other T carbon-like structures.
m symmetry. At 0 GPa, the equilibrium lattice parameters of Y-II carbon are a = 4.8302 Å. Two inequivalent atoms occupy the crystallographic 8e and 2a sites in the unit cell, which are (0.178, 0.178, 0.178) and (0, 0, 0) positions. The equilibrium lattice parameters of Y-II carbon are a = 7.7216 Å. One inequivalent atom occupy the crystallographic 8e site in the unit cell, which are (0.197, 0.197, 0.197) and (0.079, 0.079, 0.079) positions. The interspaces of T-II carbon, Y-II carbon and TY-II carbon also become smaller than that of their original structures. The equilibrium density of T-II carbon (2.955 g cm−3) is larger than that of T carbon (1.50 g cm−3) and smaller than that of diamond (3.49 g cm−3). The descending order of equilibrium densities is c-diamond (3.49 g cm−3) → M carbon (3.34 g cm−3) → bct-C4 carbon (3.32 g cm−3) → T-II carbon (2.955 g cm−3) → C6 carbon (2.85 g cm−3) → C20 carbon (2.81 g cm−3) → Y-II carbon (1.77 g cm−3) → T carbon (1.50 g cm−3) → TY-II carbon (1.05 g cm−3) → Y carbon (0.892 g cm−3) → TY carbon (0.52 g cm−3). It is well known that the densities of materials are critical for mechanical properties of materials.16 The T-II carbon has the bigger density among T carbon-like structures. So we can expect that the T-II carbon has better mechanical properties than other T carbon-like structures.
In an effort to assess the thermodynamic stability of the T carbon-like structures, we calculated the total energy per atom against the volume per atom for T carbon, T-II carbon, Y carbon, Y-II carbon, TY carbon, TY-II carbon, hexagonal diamond, cubic diamond, graphite, M carbon, C20 and C6 as shown in Fig. 2. The presence of single minimum value of total energy per atom of T-II carbon, Y-II carbon and TY-II carbon indicates that three T carbon-like structures are thermodynamic stable. Fig. 2 presents that the graphite has the lowest minimum value of total energy per atom which is in well agreement with previously results.19,20 The T-II carbon has the higher minimum of total energy per atom (−7.83 eV per atom) than other carbon allotropes, indicating that the T-II carbon is also a thermodynamically metastable phase as same as T carbon.
 | ||
| Fig. 2 The total energy per atom as a function of volume per atom for T carbon, T-II carbon, Y carbon, Y-II carbon, TY carbon, TY-II carbon, cubic diamond, graphite, C20, and C6. | ||
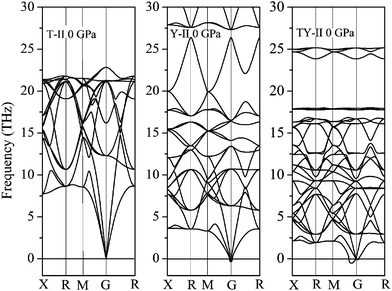
To confirm the stability of three T carbon-like structures, their lattice dynamics should also be checked. It can be found that no imaginary frequencies are observed throughout the whole Brillouin zone in T-II carbon, confirming dynamical stability of T-II carbon as shown in Fig. 3. The T-II carbon is stable at above 0 GPa and up least to 50 GPa. However, the Y-II carbon and TY-II carbon is not stable at 0 GPa because of the presence of imaginary frequencies at G point and G–M direction, respectively, as shown in Fig. 3. The calculated highest optical phonon frequency of T-II carbon at G point is mainly from the carbon–carbon bond stretching mode with a frequency of 1716 cm−1, larger than that of diamond (1295 cm−1), indicating a relatively strong carbon–carbon bonding in T-II carbon.
The mechanical stabilities were studied to confirm their structural validity. To guarantee the mechanical stability of a structure, the corresponding elastic constants should satisfy the elastic stability criteria. For a stable cubic structure, its three independent elastic constants (C11, C44, and C12) should satisfy the following generalized Born stability criteria:33 C11 > 0, C44 > 0, C11 − C12 > 0, C11 + 2C12 > 0. The elastic constants are calculated by the strain–stress method as shown in Table 1. The calculated elastic constants Cij of T-II and Y-II carbon all satisfy the mechanical stability criteria, suggesting they are mechanically stable at ambient pressure. However, the C44 value of TY-II carbon is equal to zero which indicates that the TY-II carbon is not stable at ambient condition. In the following text, we only study the stable T-II carbon.
| Cij (GPa) | C11 | C12 | C44 | B | G | ρ (g cm−3) |
|---|---|---|---|---|---|---|
| T carbon | 198 | 143 | 69 | 162 | 52 | 1.50 |
| T-II carbon | 560 | 182 | 228 | 307 | 213 | 1.77 |
| Y carbon | 92 | 80.7 | 19 | 84.4 | 13.7 | 0.89 |
| Y-II carbon | 188.5 | 162.5 | 38.2 | 171.2 | 28.1 | 1.77 |
| TY carbon | 58 | 53 | 3.2 | 54.7 | 2.9 | 0.52 |
| TY-II carbon | 113.3 | 108.0 | 0 | 109.8 | 1.2 | 1.05 |
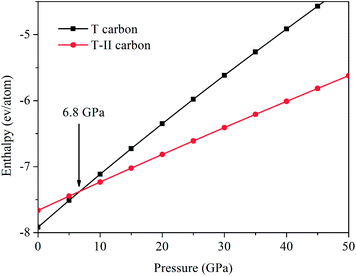
The enthalpy calculations indicate that the T-II carbon structure is more stable than T carbon at above 6.8 GPa as shown in Fig. 4. So T-II carbon is expected to be synthesized by high pressure technique. Electronic band structures show the top of valence bands of T-II carbon is located at the R point. The bottom of conduction bands is located at the Gamma point. As shown in Fig. 5, the T-II carbon is semiconductor with indirect band gap of 0.88 eV which is much smaller than that of T carbon (3.0 eV). It is noteworthy that the band gaps of T carbon-like structures are underestimated by using the semi-local functionals. The hybrid functionals can remedy this effect very well.34,35 The total electronic density of state (DOS) and projected DOS of T-II carbon shows that significant overlaps can be found between C-2s and C-2p curves, which indicate the strong sp3 hybridized covalent bonding states exist in T-II carbon. This is similar to T carbon.
By considering each carbon tetrahedron as an artificial superatom, the T carbon can be seen as a diamond structure.21 With the same idea, we found that the T-II carbon can be seen as a body central cubic structure. So the T-II carbon has the more compact atom arrangement than T carbon.
By fitting the calculated total energy as a function of volume to the third-order Birch–Murnaghan equation,36 we gain the bulk modulus (B0) of T-II carbon as 302 GPa, which is larger than that of T carbon (175 GPa)19 and is much smaller than that of diamond (466 GPa). So it can be expect that the T-II carbon has better mechanical properties than T carbon. The T-II carbon possesses cubic crystal symmetry, the stiffness constants C11 can be directly related to the crystallographic a(b, c) axes. We found an extremely large C11 (560 GPa) of T-II carbon which indicates the high incompressibility along the principal axis in the cubic T-II carbon. The calculated P–V relations (EOS) of T-II carbon together with diamond, c-BN, and other carbon allotropes confirm this point as shown in Fig. 6. The T-II carbon has stronger incompressibility among T carbon-like structures due to the compact arrangement of carbon atoms of T-II carbon in the three-dimensional space. However, the incompressibility of T-II carbon is still weaker than that of diamond, c-BN, and other carbon allotropes. The T-II carbon also has a big C44 (228.3 GPa) than other T carbon-like structures. This indicates that the T-II carbon has relatively strong shear strength. The bulk modulus and shear modulus are two important parameters to represent the superhard materials.37–39 The bulk modulus (B) measures resistance of a material against volume change under hydrostatic pressure, which indicates the average bond strength of material. The bulk modulus of T-II carbon (307 GPa) calculated from the elastic constants is in excellent agreement with the obtained equilibrium bulk modulus (302 GPa) from the equation of state. This is an evidence of reliability and accuracy of our calculated elastic constants for T carbon-like structures. The shear modulus (G) represents the resistance to shape change caused by shearing force, which indicates the resistance to change in the bond angle, and it is found that the shear modulus of T-II carbon (213 GPa) is larger than that of other T carbon-like structures. This also indicates that the T-II carbon has better mechanical properties among T carbon-like structures. The hardness of T-II carbon has been calculated by the Chen's hardness model40 which is seen as the good method for the highly anisotropic distribution of quasi-sp3-like carbon–carbon hybrids structures. The Vickers hardness Hv of T-II carbon is 27 GPa. This value is much larger than the hardness of T carbon (5.6 GPa).
 | ||
| Fig. 6 The pressure dependence of cell volume for T-II carbon, diamond, c-BN, and other carbon allotropes. | ||
In order to confirm the hardness of T-II carbon, we have investigated the ideal tensile strength along the [001] direction and the ideal shear strength along the (100)[001] slip system and to compare them with that of T carbon as shown in Fig. 7. The calculated tensile strength and shear strength of T carbon are in very good agreement with the previous results,21 indicating that our ideal strength calculations are accurate. We found that the tensile strength of T-II carbon along the [001] direction is 76 GPa and the shear strength of T-II carbon in the (100)[001] slip system is 34 GPa. The Vickers hardness of T-II carbon is very close to the shear strength in (100)[001] slip system. This can confirm the accuracy of our calculation for the hardness of T-II carbon.
To further understand the bonding mechanisms and mechanical properties of T-II carbon, electron localization function (ELF)41–43 in the specific directions has been calculated as shown in Fig. 8. The ideal strength calculations indicate that the shear strain is the critical key for the hardness of T carbon and T-II carbon. The crystal structures become unstable at shear strain of 0.14 for T carbon and 0.17 for T-II carbon. It can be found that there is strong covalent bonding characteristic between A and B atoms at shear strain of zero as shown in Fig. 8(a) and (d). With the shear strain increasing, the A–B bond is stretching and the bond length increasing. Fig. 8(b), (c), (e), and (f) show that the electron localization functions of A–B atoms become small with the shear strain increasing. When the stretched bonds reach to its elastic limit, the A–B bond breaks and the structure becomes unstable at shear strain of 0.2 for T-II carbon and 0.17 for T carbon. Form the ELF calculations, we can conclude that the T-II carbon and T carbon has the same resistant mechanism to shear strain. The T-II carbon has better resistant ability to shear strain than that of T carbon. So the T-II carbon has big hardness than T carbon.
Conclusions
In summary, the structures, mechanical properties, and dynamical properties of T carbon-like structures were extensively studied by first-principles calculations within density functional theory. We have predicted a novel modulated T carbon-like carbon allotrope with space group Pn![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. We name it as T-II carbon, which has the smallest unit of T carbon. The calculations of mechanical and electronic properties show that T-II carbon is a semiconductor with an indirect band gap about 0.88 eV. And the T-II carbon has a larger density and a more compact atoms arrangement than T carbon. The ideal strength calculations indicate that the T-II carbon has better resistant ability to shear strain among T carbon-like structures. The electron localization function calculations confirm that the bonds of T carbon break much earlier than that of T-II carbon in the (100)[001] shear direction. So the Vickers hardness of T-II carbon is much larger than that of T carbon. The present results provide insights for understanding the T carbon-like structures.
m. We name it as T-II carbon, which has the smallest unit of T carbon. The calculations of mechanical and electronic properties show that T-II carbon is a semiconductor with an indirect band gap about 0.88 eV. And the T-II carbon has a larger density and a more compact atoms arrangement than T carbon. The ideal strength calculations indicate that the T-II carbon has better resistant ability to shear strain among T carbon-like structures. The electron localization function calculations confirm that the bonds of T carbon break much earlier than that of T-II carbon in the (100)[001] shear direction. So the Vickers hardness of T-II carbon is much larger than that of T carbon. The present results provide insights for understanding the T carbon-like structures.
Acknowledgements
This work was supported by the National Basic Research Program of China (no. 2011CB808200), Program for Changjiang Scholars and Innovative Research Team in University (no. IRT1132), National Natural Science Foundation of China (nos 51032001, 11074090, 10979001, 51025206), and National Found for Fostering Talents of basic Science (no. J1103202). Parts of calculations were performed in the High Performance Computing Center (HPCC) of Jilin University.Notes and references
- Q. Li, Y. Ma, A. Oganov, H. Wang, H. Wang, Y. Xu, T. Cui, H.-K. Mao and G. Zou, Phys. Rev. Lett., 2009, 102, 175506 CrossRef.
- K. Umemoto, R. M. Wentzcovitch, S. Saito and T. Miyake, Phys. Rev. Lett., 2010, 104, 125504 CrossRef.
- J.-T. Wang, C. Chen and Y. Kawazoe, Phys. Rev. Lett., 2011, 106, 075501 CrossRef.
- Z. Zhao, B. Xu, X.-F. Zhou, L.-M. Wang, B. Wen, J. He, Z. Liu, H.-T. Wang and Y. Tian, Phys. Rev. Lett., 2011, 107, 215502 CrossRef.
- M. Amsler, J. A. Flores-Livas, L. Lehtovaara, F. Balima, S. A. Ghasemi, D. Machon, S. Pailhès, A. Willand, D. Caliste, S. Botti, A. San Miguel, S. Goedecker and M. A. L. Marques, Phys. Rev. Lett., 2012, 108, 065501 CrossRef.
- D. Li, K. Bao, F. Tian, Z. Zeng, Z. He, B. Liu and T. Cui, Phys. Chem. Chem. Phys., 2012, 14, 4347–4350 RSC.
- C. He, L. Sun, C. Zhang, X. Peng, K. Zhang and J. Zhong, Phys. Chem. Chem. Phys., 2012, 14, 8410–8414 RSC.
- C. He, L. Sun, C. Zhang, X. Peng, K. Zhang and J. Zhong, Solid State Commun., 2012, 152, 1560–1563 CrossRef CAS PubMed.
- W. L. Mao, H. K. Mao, P. J. Eng, T. P. Trainor, M. Newville, C. C. Kao, D. L. Heinz, J. Shu, Y. Meng and R. J. Hemley, Science, 2003, 302, 425–427 CrossRef CAS PubMed.
- X.-F. Zhou, G.-R. Qian, X. Dong, L. Zhang, Y. Tian and H.-T. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 134126 CrossRef.
- D. Selli, I. Baburin, R. Martoňák and S. Leoni, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 161411 CrossRef.
- H. Niu, X.-Q. Chen, S. Wang, D. Li, W. L. Mao and Y. Li, Phys. Rev. Lett., 2012, 108, 135501 CrossRef.
- J.-T. Wang, C. Chen and Y. Kawazoe, J. Chem. Phys., 2012, 137, 024502 CrossRef PubMed.
- R. Zhou and X. C. Zeng, J. Am. Chem. Soc., 2012, 134, 7530–7538 CrossRef CAS PubMed.
- C. J. Pickard, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 014106 CrossRef.
- Q. Zhu, A. Oganov, M. Salvadó, P. Pertierra and A. Lyakhov, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 193410 CrossRef.
- F. J. Ribeiro, P. Tangney, S. G. Louie and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 172101 CrossRef.
- M. Hu, F. Tian, Z. Zhao, Q. Huang, B. Xu, L.-M. Wang, H.-T. Wang, Y. Tian and J. He, J. Phys. Chem. C, 2012, 116, 24233–24238 CAS.
- X.-L. Sheng, Q.-B. Yan, F. Ye, Q.-R. Zheng and G. Su, Phys. Rev. Lett., 2011, 106, 155703 CrossRef.
- J. Y. Jo and B. G. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075151 CrossRef.
- X.-Q. Chen, H. Niu, C. Franchini, D. Li and Y. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 121405 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev. [Sect.] B, 1965, 140, A1133–A1138 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev. [Sect.] B, 1964, 136, B864–B871 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- F. B. Tian, J. H. Wang, Z. He, Y. M. Ma, L. C. Wang, T. Cui, C. B. Chen, B. B. Liu and G. T. Zou, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235431 CrossRef.
- D. Li, K. Bao, F. Tian, X. Jin, D. Duan, Z. He, B. Liu and T. Cui, RSC Adv., 2014, 4, 203–207 RSC.
- D. Li, F. Tian, D. Duan, K. Bao, B. Chu, X. Sha, B. Liu and T. Cui, RSC Adv., 2014, 4, 10133–10139 RSC.
- K. Parlinski, http://wolf.ifj.edu.pl/phonon.
- Z.-j. Wu, E.-j. Zhao, H.-p. Xiang, X.-f. Hao, X.-j. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115 CrossRef.
- B. G. Janesko, J. Chem. Phys., 2011, 134, 184105 CrossRef PubMed.
- B. M. Wong and J. G. Cordaro, J. Phys. Chem. C, 2011, 115, 18333–18341 CAS.
- F. Birch, J. Appl. Phys., 1938, 9, 279–288 CrossRef PubMed.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354 CrossRef.
- A. Reuss, Z. Angew. Math. Mech., 1929, 9, 49–58 CrossRef CAS.
- W. Voigt, Lehrburch der Kristallphysik, Teubner, Leipzig, 1928 Search PubMed.
- X.-Q. Chen, H. Niu, D. Li and Y. Li, Intermetallics, 2011, 19, 1275–1281 CrossRef CAS PubMed.
- B. Silvi and A. Savin, Nature, 1994, 371, 683–686 CrossRef CAS.
- A. Savin, O. Jepsen, J. Flad, O. K. Andersen, H. Preuss and H. G. von Schnering, Angew. Chem., Int. Ed., 1992, 31, 187–188 CrossRef.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2014 |