DOI:
10.1039/C4RA01875C
(Paper)
RSC Adv., 2014,
4, 24533-24537
Enhanced electrocaloric effect in a Ba(1−x)SrxTiO3 compositionally graded film
Received
4th March 2014
, Accepted 7th May 2014
First published on 7th May 2014
Abstract
An enhanced electrocaloric (EC) effect is observed in a 300 nm compositionally graded Ba(1−x)SrxTiO3 (BST) film prepared by a sol–gel method. It is found that the maximum EC effect in the compositionally graded films is much larger than that in the uniform film with the same thickness and external field. We infer that the enhanced EC effect is attributed to internal strains and space charge accumulation existing at the interfaces of the compositionally graded film. A thermodynamic model is developed to investigate our deduction, and the results are in agreement with the experimental results.
1. Introduction
The temperature and entropy of ferroelectric materials can be changed with the applied electric field under adiabatic conditions, which is called the electrocaloric (EC) effect. The EC effect has attracted great interest over the past decades because it can be used to fabricate domestic and industrial refrigeration, which can effectively reduce greenhouse gases and energy consumption. Previous studies on the EC effect focused on bulk ceramics and single crystals;1,2 however, their breakdown fields are too low to get a big enough EC effect for commercial applications. Recently, giant EC effects have been obtained because of the realization of ultrahigh electric fields in ferroelectric thin films3–6 such as PbZr0.95Ti0.05O3 (PZT) and PVDF–TrFE films, which induce large entropy changes near ferroelectric–paraelectric (FE–PE) phase transitions. The observation of giant EC effects in thin films renews the interest in investigating the EC effect in ferroelectric materials.
However, up to now, most of the experimental and theoretical investigations on the EC effect have been focused on uniform composition films. Indeed, compared to conventional homogeneous ferroelectrics, the ferroelectric heterostructure possessing internal stresses and asymmetry at different interfaces always undergoes great improvements to functional characteristics such as ferroelectric,7 dielectric properties,8–11 and effective pyroelectric response.12 However, the EC effects in compositionally graded films have not been investigated systematically. Hence, we expected that the EC effect in compositionally graded films could be interesting and useful.
Barium strontium titanate [Ba(1−x)SrxTiO3 (BST)] is an important lead-free ferroelectric because of its low and easily controlled Curie temperature,13 which implies that it has a large EC effect for refrigeration at room temperature. F. Jin et al. obtained a giant pyroelectric coefficient from the BST-graded ferroelectric film.12 Hence, as the converse effect of pyroelectricity, the EC effect in the compositionally graded BST thin film can be greatly improvement compared to the uniform BST films. In this work, we thus investigate the EC effect of the compositionally graded BST thin film and discuss its enhancement mechanism in detail.
2. Experiments
BST precursor solutions were synthesized by barium acetate, strontium acetate and titanium butoxide, and the Ba/Sr molar ratios are 7/3, 8/2 and 9/1, respectively. Titanium butoxide was dissolved in glycol methyl ether with 2–3 drops of acetylacetone to form the chelate complex. Appropriate amounts of barium acetate and strontium acetate were mixed and stirred in acetic acid at 60 °C until all the particles were dissolved. Then, the above two solutions were mixed and stirred for 5 hours at 60 °C to form 0.15 M BST precursor solutions, and these solutions were aged at room temperature for about 5 days. The compositionally graded Ba0.7Sr0.3TiO3/Ba0.8Sr0.2TiO3/Ba0.9Sr0.1TiO3 film and the uniform BST film were deposited on Pt/Ti/SiO2/Si substrates by the spin coating of BST precursor solutions at 4000 rpm for 40 s. First, the film was heated to 180 °C for 5 min at a heating rate of 20 °C s−1 and then the temperature was increased to 550 °C to pre-anneal the film for 5 min. Finally, the temperature was raised to 750 °C to anneal the film for 10 min. Such a spining–drying–annealing cycle was repeated six times to achieve the desired film thickness of 300 nm. To prepare the compositionally graded films, Ba0.7Sr0.3TiO3 was deposited as the first compositional layer and then Ba0.8Sr0.2TiO3 and Ba0.9Sr0.1TiO3 were successively deposited, and the thickness of each compositional layer was the same. The P–E hysteresis loops at various temperatures were evaluated by an RT66A ferroelectric test system with a MMR temperature microprobe station.
Hysteresis loops of the compositionally graded Ba0.7Sr0.3TiO3/Ba0.8Sr0.2TiO3/Ba0.9Sr0.1TiO3 film and the uniform BST film at different temperatures are shown in Fig. 1(a)–(d). Electrical hysteresis measurements were made roughly every T = 10 °C in the temperature range from 390 K to 240 K on cooling to minimize reductions in P due to fatigue. According to Fig. 1, the curve becomes lean, and the polarization P drops as the temperature increases, which indicates a gradual transition from the ordered ferroelectric state to the disordered paraelectric state.
 |
| | Fig. 1 Hysteresis loops under different temperatures in (a) the compositionally graded BST film (b) Ba0.9Sr0.1TiO3 film, (c) Ba0.8Sr0.2TiO3 film and (d) Ba0.7Sr0.3TiO3 film (inset). The P(T) of each film under the selected fields at different temperatures. | |
3. Results and discussion
The temperature dependence of (∂P/∂T)E was obtained from the fourth polynomial fits of the P–T curve under different fields (inset of the Fig. 1). According to the Maxwell relation (∂P/∂T)E = (∂S/∂E)T, the reversible adiabatic changes ΔT can be computed using the following relation:3| |
 | (1) |
where CE is the heat capacity per unit volume; the value of CE = 3.05 × 106 J K−1 m−3 reported for the similar compound BaTiO3 (ref. 14) was used here. E1 and E2 are the initial and final applied electric fields, respectively. Since no antiferroelectric–ferroelectric phase transition of BST exists in the temperature range of interest, there is no need to avoid the antiferroelectric regime. Therefore, E1 can be as low as zero, which is sufficient to ensure dP/dT < 0.15 As shown in Fig. 1, we the P(T) of each film is shown under E1 = 0 kV cm−1 and E2 = 350 kV cm−1.
The EC temperature changes of uniform and compositionally graded BST films obtained with eqn (1) are presented in Fig. 2, respectively. The largest adiabatic temperature changes of Ba0.7Sr0.3TiO3, Ba0.8Sr0.2TiO3 and Ba0.9Sr0.1TiO3 were 1.56 K at Tpeak = 278 K, 1.75 K at Tpeak = 314 K, 1.9 K at Tpeak = 350 K, respectively. On the other hand, the largest adiabatic temperature change of the compositionally graded BST film is 3.2 K at Tpeak = 290 K. Compared to the same ratio of Ba/Sr of the uniform Ba0.8Sr0.2TiO3 film, the Tpeak of the EC effect on the compositionally graded BST film is nearer to the room temperature than that of the thin BST films. In a word, the EC effect gets a dominant enhancement in the compositionally graded BST film.
 |
| | Fig. 2 Electrocaloric temperature changes ΔT of compositionally graded films and uniform BST films due to the applied electric field ΔE. | |
In previous reports,16–18 the enhancement of the functional characteristics in the compositionally graded film was attributed to internal strains and internal electric field caused by asymmetry interfaces. In general, the internal strains and electric field have been proven to greatly influence the EC effect.19 Hence, we considered that the differences of the EC effect between uniform and compositionally graded BST films are due to the internal strains and internal electric field.
Based on the above discussion, a thermodynamic model was developed to investigate the EC effect of the compositionally graded BST films. We focused on the composition consisting of BST compositionally graded ferroelectrics layers, in which the thicknesses of Ba0.9Sr0.1TiO3, Ba0.8Sr0.2TiO3 and Ba0.7Sr0.3TiO3 are hA, hB and hC, respectively. The self-strains derived from the lattice parameter mismatch and the difference between the thermal expansion coefficients of the film and substrate have been considered here. Meanwhile, the differences of the polarization between these layers create an internal electric field in the compositionally graded BST films. The free-energy density F of the compositionally graded BST film can be expressed as follows:
| | |
F = βAFA + βBFB + βCFC,
| (2) |
where
βA =
hA/(
hA +
hB +
hC) is the thickness fraction of Ba
0.9Sr
0.1TiO
3. In our experiment, the thickness of each layer is approximately equal. Hence, in our calculation here, we take
βA =
βB =
βC = 1/3.
FA,
FB and
FC are the energy density of the ferroelectric layers of Ba
0.9Sr
0.1TiO
3, Ba
0.8Sr
0.2TiO
3 and Ba
0.7Sr
0.3TiO
3, respectively. The total free-energy density
Fγ (γ = A, B and C) can be defined as
20,21| |
 | (3) |
where
| |
 | (4) |
| |
 | (5) |
| |
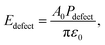 | (6) |
| |
 | (7) |
| |
 | (8) |
| |
 | (9) |
where
αγi,
αγij and
αγijk are the stiffness coefficients at constant stress,
Qγij is the electrostrictive constant,
uγ is the misfit strain of layer γ with respect to neighboring layers,
ar is the in-plane lattice parameters of ferroelectric layers,
aS is the lattice parameter of the substrate,
Pdefect is the local defect polarization induced by oxygen vacancies,
Edefect is the defect dipole,
A0 is a constant equal to 1.02.
22 Edefect, which is in the opposite direction of the external field, will decrease Δ
E, which is an important factor influencing the EC effect. All the coefficients mentioned above are assumed to be independent of the temperature, except the dielectric stiffness constant
αγ3 = (
T −
T0)/2
ε0C0, where
T and
T0 are the temperature and Curie temperature, respectively,
ε0 is the vacuum permittivity and
C0 is the Curie constant. The electric fields
Eγ3 inside the layers, which is caused by the difference of polarization between layers, is given by
23| | |
EA3 = (βAPA3 + βBPB3 + βCPC3 − PA3)/ε0 = (PB3 + PC3 − 2PA3)/3ε0,
| (10) |
| | |
EB3 = (βAPA3 + βBPB3 +βCPC3 − PB3)/ε0 = (PA3 + PC3 − 2PB3)/3ε0,
| (11) |
| | |
EC3 = (βAPA3 + βBPB3 + βCPC3 − PC3)/ε0 = (PA3 + PB3 − 2PC3)/3ε0.
| (12) |
Then, the polarization state of the compositionally graded film and its dependence on the temperature, misfit strain and thickness fraction can be determined by the equilibrium condition ∂F/∂Pγ = 0. The excess entropy SE of the compositionally graded film can be expressed as SE = βASA + βBSB + βCSC, where the excess entropy of the ferroelectric sub-layers is
| |
 | (13) |
When an external electric field Ea is applied perpendicular to the surface of the thin film, the electrocaloric coefficient p is defined as
| |
 | (14) |
The reversible adiabatic changes ΔT of the compositionally graded film can be calculated by eqn (1), and the temperature change curves are shown in Fig. 3. In our calculation, the thermodynamic coefficients, elastic stiffnesses, and electrostrictive constant of the BaxSr1−xTiO3 are listed as follows:24–26
| | |
αγ3 = 1.12 × 107 × (T − 371x + 253)/(9x + 8)
| (15) |
| | |
αγ11 = (−11.96x + 8.4) × 109
| (16) |
| | |
Sγ12 = −1.57 × 10−12
| (19) |
where
x = 0.7, 0.8, 0.9, respectively. The heat capacity
CE = 3.05 × 10
6 J K
−1 m
−3 reported for a similar compound BaTiO
3 (
ref. 14) is used here, and it remains a constant in the range of temperature which we investigated. The adiabatic temperature change of the compositionally graded and uniform BST films with the electric field difference Δ
E = 350 kV cm
−1, which is the same as our experiment, is shown in
Fig. 3. This result coincides with our experiment result. The internal field caused by oxygen vacancies decreases the EC effect on the BST single composition film, while “charge pumping” in compositionally graded BST films can restrain the internal field. The misfit strains in ferroelectric layers have been proven to greatly influence the electrocaloric effect. As a result, it causes the difference of the EC effect between the BST single composition film and compositionally graded films.
 |
| | Fig. 3 Difference in the electrocaloric effect between the uniform and compositionally graded BST films as a function of the interaction with misfit strain and the internal field caused by the oxygen vacancies and “charge pumping” in compositionally graded BST films. | |
According to our theoretical research, misfit strains can have a great influence on ΔT and Tpeak between uniform and compositionally graded BST films. The influence of misfit strains on the magnitude of the EC effect and temperature change has been discussed many times.19,27,28 A compressive misfit strain shifts the maximum of the EC effect to higher temperature, while the tensile misfit strain results in the opposite effect. Because the diameter of Ba is greater than that of Sr, the lattice constant of BST films increases with the increasing ratio of Ba. In the compositionally graded BST film, the lattice constant of the bottom layer Ba0.7Sr0.3TiO3 is smaller than that of Ba0.9Sr0.1TiO3, which makes the compositionally graded BST film suffer from a tensile misfit strain. As a result, the Tpeak of the compositionally graded BST film is nearer to room temperature.
In our calculation, the EC effect can be enhanced under the effect of the internal electric field, which is caused by the “charge pumping” in compositionally graded films, and this enhancement is connected with the entropy changes caused by charge movement. As we know, the EC effect is closely related to the change in the entropy of the film:29 when under an applied external field, the dipoles realign with the field, resulting in the appearance of induced polarization; this ordering alignment leads to a decrease in the entropy. When the external field is removed under adiabatic conditions, the dipole becomes disordered, thereby inducing a great increase of entropy, which in turn decreases the temperature of the dielectric material. In the compositionally graded film, the distribution of polarization in these ferroelectric materials is asymmetric and graded, which will lead to the charges being preferentially “pumped” to the electrode or interfaces between layers. In this case, the entropy decreases because the charges become ordered. While under adiabatic conditions, the discrepancy of polarization between layers is diminished by removing the external field. As a result, the charges are pumped into the interface, and they become free charges, which leads to the charges being completely disordered. As shown in Fig. 4, such a disorder statement is associated with a large entropy change, and this explains the impact on the EC effect by space charge accumulation in the compositionally graded film.
 |
| | Fig. 4 Free charge movement under the external electric field. | |
4. Conclusions
In summary, the EC effect on the lead-free uniform and compositionally graded BST thin films has been demonstrated here. We prepared 300 nm thin and compositionally graded BST films using a sol–gel method. The EC effect peak adiabatic temperature change of the compositionally graded BST film is 3.2 K, which is greater than the largest adiabatic temperature change in uniform BST films (ΔT = 1.9 K). The differences are attributed to the misfit strain, the field induced by the oxygen vacancy and the initial field caused by the difference of polarization between layers in the compositionally graded film. Reducing the Sr content in BST will reduce the ferroelectric transition temperature to an even lower temperature, which suggests a means to achieve significant EC effects at even lower temperature.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (no. 11272274, 11372266 and 11032010), the Hunan Provincial Natural Science Foundation of China (no. 12JJ1007), the Specialized Research Fund for the Doctoral Program of Higher Education (no. 20114301110004) and the Foundation for the Author of National Excellent Doctoral Dissertation of PR China (201143).
References
- B. A. Tuttle and D. A. Payne, Ferroelectrics, 1981, 37, 603 CrossRef CAS.
- D. Q. Xiao, Y. C. Wang, R. L. Zhang, S. Q. Peng, J. G. Zhu and B. Yang, Mater. Chem. Phys., 1998, 57, 182 CrossRef CAS.
- A. S. Mischenko, Q. Zhang, J. F. Scott, R. W. Whatmore and N. D. Mathur, Science, 2006, 311, 1270 CrossRef CAS PubMed.
- B. Neese, B. Chu, S. G. Lu, Y. Wang, E. Furman and Q. M. Zhang, Science, 2008, 321, 821 CrossRef CAS PubMed.
- A. S. Mischenko, Q. Zhang, R. W. Whatmore, J. F. Scott and N. D. Mathur, Appl. Phys. Lett., 2006, 89, 242912 CrossRef PubMed.
- H. Chen, T.-L. Ren, X.-M. Wu, Y. Yang and L.-T. Liu, Appl. Phys. Lett., 2009, 94, 182902 CrossRef PubMed.
- P. Chakraborty and S. B. Krupanidhi, J. Appl. Phys., 2010, 107, 124105 CrossRef PubMed.
- M. B. Okatan, J. V. Mantese and S. P. Alpay, Acta Mater., 2010, 58, 39 CrossRef CAS PubMed.
- M. W. Cole, E. Ngo, S. Hirsch, M. B. Okatan and S. P. Alpay, Appl. Phys. Lett., 2008, 92, 072906 CrossRef PubMed.
- M. B. Okatan, A. L. Roytburd, J. V. Mantese and S. P. Alpay, J. Appl. Phys., 2009, 105, 114106 CrossRef PubMed.
- X. Hao and Z. Zhang, et al., J. Alloys Compd., 2010, 501, 358 CrossRef CAS PubMed.
- F. Jin, G. W. Auner and R. Naik, Appl. Phys. Lett., 1998, 73, 2838 CrossRef CAS PubMed.
- O. G. Vendik and S. P. Zubko, J. Appl. Phys., 2000, 88, 5343 CrossRef CAS PubMed.
- G. Akcay, S. P. Alpay, J. V. Mantese and G. A. Rossetti, Appl. Phys. Lett., 2007, 90, 252909 CrossRef PubMed.
- H. Chen, T.-L. Ren, X.-M. Wu, Y. Yang and L.-T. Liu, Appl. Phys. Lett., 2009, 94, 182902 CrossRef PubMed.
- A. L. Roytburd and S. P. Alpay, et al., Appl. Phys. Lett., 2005, 87, 092902 CrossRef PubMed.
- M. W. Cole, E. Ngo and S. Hirsch, et al., J. Appl. Phys., 2007, 102, 034104 CrossRef PubMed.
- S. Zhong, S. P. Alpay and M. W. Cole, et al., Appl. Phys. Lett., 2007, 90, 092901 CrossRef PubMed.
- G. Akcay and S. P. Alpay, et al., J. Appl. Phys., 2008, 103, 024104 CrossRef PubMed.
- N. A. Pertsev, A. G. Zembilgotov and A. K. Tagantsev, Phys. Rev. Lett., 1998, 80, 1991 CrossRef.
- B. Li and J. B. Wang, et al., EPL, 2011, 95, 67004 CrossRef.
- Y. Zhang, J. Y. Li and D. N. Fang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 64103 CrossRef.
- M. B. Okatan, J. V. Mantese and S. P. Alpay, Acta Mater., 2010, 58, 39 CrossRef CAS PubMed.
- Z.-G. Ban and S. P. Alpay, Phys. Rev. B: Condens. Matter. Phys., 2003, 67, 184104 CrossRef.
- Y. Zhang and J. Li, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 064103 CrossRef.
- P. Erhart and R. -Albert Eichel, Phys. Rev. B: Condens. Matter, 2007, 76, 174116 CrossRef.
- X. Zhang and J. B. Wang, et al., J. Appl. Phys., 2011, 109, 126102 CrossRef PubMed.
- J. Zhang and S. P. Alpay, et al., Appl. Phys. Lett., 2011, 98, 132907 CrossRef PubMed.
- S. Lisenkov and I. Ponomareva, Phys. Rev. B: Condens. Matter, 2009, 80, 140102 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.