Design of 3D 1,3,5,7-tetraphenyladamantane-based covalent organic frameworks as hydrogen storage materials†
Abstract
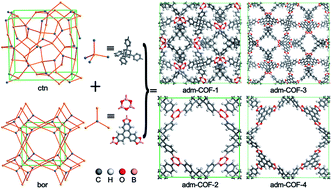
A new type of 1,3,5,7-tetraphenyladamantane-based covalent organic framework (adm-COF) was designed under the ctn and bor net topology with the method of molecular mechanics. The computed results reveal that all four designed adm-COFs exhibit extremely high porosity (86–95%) and large H2 accessible surface area (5967–6709 m2 g−1). The grand canonical Monte Carlo method was employed to simulate the adsorption isotherms of H2 gas in these adm-COFs at 77 K and 298 K. The simulated results indicate that, at 77 K and 100 bar, adm-COF-4 has the highest gravimetric H2 adsorption capacity of 38.36 wt%, while adm-COF-1 has the highest volumetric H2 adsorption capacity of 60.71 g L−1. Impressively, the gravimetric H2 adsorption capacity of adm-COF-1 can reach up to 5.81 wt% under 100 bar at room temperature, which is very close to the criterion of 6 wt% for the practical application of hydrogen at room temperature set by the U.S. Department of Energy. In addition, possible schemes for synthesizing these adm-COFs have been proposed.

 Please wait while we load your content...
Please wait while we load your content...