Ferroelectric domain morphology and temperature-dependent piezoelectricity of (K,Na,Li)(Nb,Ta,Sb)O₃ lead-free piezoceramics

Abstract

Domain morphology and temperature-dependent piezoelectricity in terms of piezoelectric coefficient d₃₃ and normalized strain d₃₃* of (K,Na,Li)(Nb,Ta,Sb)O₃ lead-free piezoceramics at the polymorphic phase boundary were investigated. Transmission electron microscopy (TEM) and piezoresponse force microscopy (PFM) studies revealed a characteristic domain morphology comprising strip-like domains and featureless domains. Moreover, a facile method based on the field-dependent piezoelectric coefficient d₃₃(E) measurement was verified to characterize in situ temperature dependence of piezoelectric coefficient d₃₃, as an alternative for the conventional ex situ route. It was demonstrated that the normalized strain d₃₃* exhibits superior thermal resistance to piezoelectric coefficient d₃₃, though both parameters are susceptible to temperature variation.

---

1 Introduction

The functionality of direct conversion between electrical and mechanical energy endows piezoelectric materials with wide-ranging applications, e.g., actuators, transducers, and sensors, etc.¹ As environmental consciousness is heightened, the currently dominating Pb(Zr,Ti)O₃ (abbreviated as PZT) family is confronted with global restrictions such as the WEEE directive (Waste of Electrical and Electronic Equipment) and the RoHS directive (Restriction of certain Hazardous Substances) due to the large portion of hazardous lead substance it contains, albeit its superior piezoelectric performance. Therefore, the last decade has witnessed considerable dedication devoted to developing high-end lead-free counterparts to substitute for PZT.^2–8

The breakthrough achieved by Saito et al.⁸ in textured (K,Na)NbO₃ (KNN)-based lead-free piezoceramics with remarkable piezoelectricity crowned this system with enormous opportunities to be one of the most promising candidates, and accordingly triggered worldwide interest.^2,3,6 Most of the research concentrated on tailoring the piezoelectric performance via compositional modification^9,10 or domain engineering,^11,12 which are actually related to manipulating the polymorphic phase transition (PPT) around room temperature. It is generally agreed that the increased polarization directions in the PPT region benefit the enhancement of piezoelectric performance at ambient temperature.^13,14 Furthermore, contributions originating from domain hierarchy¹⁵ resemble that in lead-based¹⁶ and lead-free¹⁷ counterparts with the distinct phase structures of a morphotropic phase boundary (MPB). It is proved that transmission electron microscopy (TEM) is a powerful tool to uncover the domain hierarchy,¹⁵ while piezoresponse force microscopy (PFM) can deliver fruitful information about the domain orientation.^14,18 A combination of TEM and PFM techniques may provide more a perspicuous schema of domain morphology, which has been rarely reported for KNN. However, industrial implementation demands not only the good piezoelectric performance at room temperature but also its stability in response to ambient changes. In contradiction to the temperature-independent MPB in PZT systems, the PPT in KNN-based ceramics is considered to have the drawback of high sensitivity to temperature fluctuation, which is unfavorable for practical applications.^19–21 Therefore, it is necessary to carefully evaluate the temperature-dependent piezoelectricity of KNN-based ceramics. Nevertheless, only a few works reported the temperature-dependent piezoelectric coefficient d₃₃ of KNN-based ceramics.^22–24 Wang et al.²² showed the in situ measurement of temperature-dependent d₃₃ on a custom-designed apparatus, while an ex situ annealing-measuring route was adopted in most studies.^23,24 Thus, it would be attractive to both scientific and technological domains if a simple method can be developed to characterize the in situ temperature dependence of d₃₃.

In the present study, domain morphology and temperature-dependent piezoelectric response of (K,Na,Li)(Nb,Ta,Sb)O₃ (KNNLTS) ceramics were investigated systematically. A featured domain morphology embodied by the coexistence of strip-like domains and featureless domains was observed by TEM and PFM. In addition, a novel and facile method based on the field-dependent piezoelectric coefficient d₃₃(E) measurement was successfully demonstrated to characterize the in situ change of piezoelectric coefficient d₃₃ with temperature.

2 Experimental

Sample preparation

Piezoceramics with the nominal composition of Li_0.02(K_0.45Na_0.55)_0.98(Nb_0.77Ta_0.18Sb_0.05)O₃ (KNNLTS) were fabricated via a conventional ceramic processing route with raw materials of K₂CO₃ (99%), Na₂CO₃ (99.8%), Li₂CO₃ (97%), Nb₂O₅ (99.95%), Ta₂O₅ (99%), and Sb₂O₃ (99%). The starting chemicals were weighted stoichiometrically and planetary ball milled for 24 h in an ethanol solution. The weight ratio between the milling balls and raw materials is about 10 : 1 and the rotational speed during ball milling is 250 min⁻¹. The slurry was dried and calcined at 850 °C for 5 h. The synthesized powders were subjected to ball milling again for another 24 h in ethanol. After drying, the powders were pressed into disks of 10 mm in diameter and 1.5 mm in thickness, followed by cold isostatic pressing under 200 MPa for 2 min. Such pellets were sintered at 1100–1120 °C in air for 2 h. For macroscopic electrical characterization, the as-sintered ceramics were polished down to 1 mm in thickness and painted with silver pastes fired at 550 °C for 30 min to form electrodes. The samples were poled under an electric field of 4 kV mm⁻¹ at 120 °C in silicone oil for 30 min.

Characterization of phase structure and electrical properties

High-resolution X-ray diffraction (XRD) measurement was conducted to determine the crystal structure by using Cu Kα radiation (Rigaku, D/Max250, Tokyo, Japan). The temperature dependence of dielectric permittivity and loss were determined using an impedance analyzer (HP 4192A, Palo Alto, CA). The piezoelectric coefficient d₃₃ was measured using a quasi-static d₃₃ meter (ZJ-3A, Institute of Acoustics, Chinese Academy of Science, Beijing, China), by which a small oscillating force is applied to the samples and the charge output is measured and divided by the applied force amplitude. The ferroelectric properties, field-dependent piezoelectric coefficient d₃₃(E) hysteresis loops, and unipolar piezoelectric strain S(E) curves were recorded on a ferroelectric tester (aixACCT TF Analyzer 1000, Germany). For the polarization P(E) hysteresis loops measurement, an electric field of 3 kV mm⁻¹ at 1 Hz was applied. The input and output signals for the field-dependent piezoelectric coefficient d₃₃(E) measurement and the unipolar piezoelectric strain S(E) measurement are illustrated in Fig. 1. The excitation signal for the field-dependent piezoelectric coefficient d₃₃(E) measurement is a continuously changing triangular-shaped base waveform of low frequency with a superimposed high frequency small signal voltage. It is an electric field with a frequency of 1 Hz and amplitude of 3 kV mm⁻¹, on which an AC voltage of 25 V and 250 Hz was superimposed, in this case. The displacement data d₀ is simultaneously captured with an additional external displacement sensor, e.g., laser interferometer according to the eqn (1):²⁵

d₀ = (λ/1.414π)(V_out/V_p–p) (1)

where λ, V_out, and V_p–p are the wavelength of monochromatic laser, the detected signal, and the peak to peak value of the interference signal, respectively. And then the field-dependent piezoelectric coefficient d_ij(E) can be derived from the displacement data using eqn (2):²⁵

d_ij(E) = (d₀/U)(t/x) (2)

where U is the driving voltage amplitude, x is the corresponding length in the direction of sample deformation, t thickness of the sample in the direction of the applied electric field. x equals t in the case of d₃₃(E) measurement. Thus the positive value at zero field in the d₃₃(E) hysteresis loops denoted by d₃₃⁰⁺ (see Fig. 1(a)) can be taken as piezoelectric coefficient d₃₃. For the piezoelectric strain S(E) measurement, a unipolar triangular-shaped electric field is applied to the specimen, and the displacement is documented at the same time. The normalized strain d₃₃* can be deduced from eqn (3):⁴

d₃₃* = S_max/E_max (3)

where E_max and S_max are the maximum applied electric field and corresponding unipolar strain output, respectively, as depicted in Fig. 1(b).

Fig. 1 Illustration of input and output signals for (a) the field-dependent piezoelectric coefficient d₃₃(E) measurement and (b) the piezoelectric strain S(E) measurement, respectively.

Details of TEM and PFM studies

The TEM specimens were prepared by mechanically polishing them to a thickness of approximately 20 μm. The central parts of the disks were further reduced by precision argon-ion milling (RES101, Leica EM, Wetzlar, Germany) at an acceleration voltage of 4 kV. These specimens were investigated using a high-resolution TEM (HRTEM JEOL 2011, Tokyo, Japan) operated at 200 kV with a point resolution of 0.19 nm. For the PFM observations, the as-sintered samples were mechanically polished to about 20 μm in thickness. The PFM experiments were carried out using a commercial atomic force microscopy (MFP-3D, Asylum Research, USA). The PFM signal was recorded at room temperature under ac voltage U_ac = 5–10 V, f_ac = 50 kHz applied to a conductive Pt–Ir coated cantilever PPP-NCHPt (Nanosensors, Switzerland). Both vertical and lateral PFM images were taken, which provide information about the distribution of out-of-plane and in-plane components of ferroelectric domains, respectively.

3 Results and discussion

The XRD pattern of KNNLTS ceramics is presented in Fig. 2(a), for which the index for an orthorhombic phase was adopted, exhibiting a typical perovskite structure. It is well-accepted that the piezoelectricity of KNN-based ceramics is greatly dependent on the phase structures, which can be roughly quantified by analyzing the relative intensities of (200) and (020) peaks (I₂₀₀/I₀₂₀) around 2θ = 45°. For randomly-oriented piezoceramics with an orthorhombic symmetry, the ideal ratio I₂₀₀/I₀₂₀ equals to 2 : 1, while it evolves to 1 : 2 for a tetragonal phase.²⁶ However, more detailed information about high-angle X-ray diffraction, such as (222) and (004) peaks, is indispensable for precise analysis of crystallographic or domain evolution.^11,26 For the present material, the I₂₀₀/I₀₂₀ ratio is slightly higher than 1 (see the enlarged peaks in the inset figure of Fig. 2(a)), indicating the coexistence of orthorhombic and tetragonal phases with orthorhombic being the dominating symmetry. The XRD results are supported by the temperature-dependent dielectric constant and loss measurement, as shown in Fig. 2(b). Two anomalies are observed around 63 °C and 238 °C in the dielectric constant curve, corresponding to the polymorphic phase transition point T_O-T and Curie temperature T_C, respectively. It should be mentioned that the dielectric measurement was conducted in a heating cycle, and the inherent thermal hysteresis usually results in higher output of T_O-T and T_C than the real values on a scale of tens of degrees Celsius. In other words, the polymorphic phase transition point T_O-T should be located near room temperature. Benefiting from the PPT effect, superior piezoelectric performance can be expected.¹³

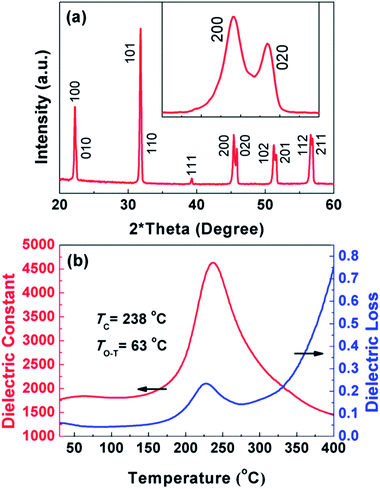Fig. 2 (a) The XRD pattern of as-sintered KNNLTS ceramics; (b) temperature dependence of dielectric permittivity and dielectric loss of poled KNNLTS ceramics.

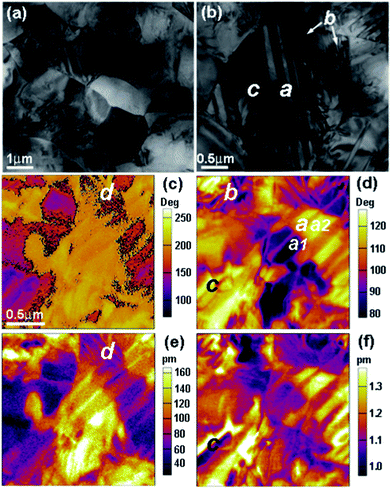
For ferroelectric polycrystals, domain morphology is closely related to piezoelectric performance.^16,27,28 In the present work, TEM and PFM were employed to explore the microstructure of KNNLTS ceramics . The TEM image displayed in Fig. 3(a) shows that the KNNLTS ceramics have typical square-shaped grains with grain sizes ranging from 1 to 3 μm. It was reported that the coexistence of orthorhombic and tetragonal phase structures at room temperature will result in complex domain patterns.¹⁵ Representative domain structures of KNNLTS piezoceramics were observed, as shown in Fig. 3(b–d). It should be noted that typical domain patterns composed of submicro- and nano-sized domains could be found in one single grain. Fig. 3(b) shows that strip-like domains with width of several hundred nanometers marked as area a and irregular-shaped (featureless) domains in nano-scale in area b coexist, agreeing well with the results reported previously.^15,29 Most intriguingly, the nano-domains with an average size of 100 nm developed in submicro-domains forming a domain hierarchy (see area c); and the angle between nano- and submicro-domain walls in the projection plane is approximately 45°, resembling that of PZT¹⁶ and BCZT³⁰ compositions with phase coexistence. It was disclosed that domain size is proportional to the square root of domain wall energy.³¹ In general, the piezoelectric effect comprises intrinsic and extrinsic contributions. The former refers to the linear piezoelectric effect of lattice displacement, while the latter relates to the movement of domain walls.³² The reduced domain wall energy renders nano-domains facilely responsive to external excitations, e.g., mechanical force or electric field, contributing as extrinsic portions.

Fig. 3 TEM analysis of typical (a) grain distribution and (b) domain configuration; (c) vertical piezoresponse force microscopy (VPFM) image and (d) lateral piezoresponse force microscopy (LPFM) image of domain morphology, and the corresponding piezoresponse amplitude of (e) VPFM and (f) LPFM modes of KNNLTS ceramics.

PFM observations are consistent with TEM outcomes, as demonstrated in Fig. 3(c–f). The vertical and lateral PFM phase images shown in Fig. 3(c) and (d) evidence that the domain morphology of KNNLTS ceramics indeed comprises strip-like ferroelastic domains (area a) and featureless nano-sized domains (area b). Fig. 3(e) and (f) present the vertical and lateral piezoresponses, respectively, which are mainly from the intrinsic components. Generally, an orthorhombic system provides twelve possible spontaneous polarizations P_s in all 〈110〉 directions, while there are six P_s in directions of 〈100〉 for a tetragonal symmetry. The angles between two polarization vectors for KNN can be 90° and 180° as in a tetragonal system or 60° and 120° for orthorhombic crystals. Combined analysis of phase and piezoresponse images can provide detailed information about domain orientations. Take the domains denoted by a1 and a2 in area a for example. The phase difference between a1 and a2 is about 50° with a larger piezoresponse observed in a1. Considering the possible domain orientations in orthorhombic-tetragonal phases coexisting KNN-based piezoceramics, a reasonable explanation is that they are 60°/120° domains for a1 and a2 with a1 lying in-plane. For domains in area c, no obvious contrast was observed in the phase image, whereas a difference in piezoresponse exists in this area, implying the presence of 90° domains. A trace of 180° domains, which show distinct contrast in phase while having the same piezoresponse in the vertical imaging mode, was also recorded in the area marked as d. However, it can be inferred from the PFM study as discussed above, that the orthorhombic phase prevails in this system, though it is proved to be a coexistence of orthorhombic and tetragonal symmetries. These findings match well with the above XRD and TEM investigations.

High piezoelectricity can be expected in the KNNLTS ceramics at ambient temperature due to the combined effects of PPT and nano-domain contributions as aforementioned. The piezoelectric coefficient d₃₃ characterized using a quasi-static d₃₃ meter reached 267 pC N⁻¹ (see Table 1), which is a relatively high value for KNN-based piezoceramics. Moreover, d₃₃ was evaluated by two other distinctive techniques: the field-dependent piezoelectric coefficient d₃₃(E) measurement and the piezoelectric strain S(E) measurement, as shown in the following.

Table 1 Comparison of d₃₃ or d₃₃* values measured by three distinctive methods at room temperature

Method	Quasi-static d33 meter	Field-dependent piezoelectric coefficient d33(E) measurement	Piezoelectric strain S(E) measurement
d33 or d33* (pC N^−1)	267 ± 7	280 ± 5	361 ± 11

---

The field-dependent piezoelectric coefficient d₃₃(E) measurement yielded a d₃₃ value of 280 pC N⁻¹ at room temperature (as listed in Table 1), slightly higher but comparable to the value obtained by a quasi-static d₃₃ meter. Recently, the equivalence between the field-dependent piezoelectric coefficient d₃₃(E) measurement and quasi-static d₃₃ meter has also been verified by Fialka et al.³³ Therefore, it may offer a facile method to evaluate the in situ temperature-dependent piezoelectric coefficient d₃₃; allowing the feasibility to measure the d₃₃(E) hysteresis loops at varied temperatures. Fig. 4(a) and (b) provide the d₃₃(E) curves and polarization hysteresis P(E) loops at different temperatures, respectively, from which the temperature dependence of piezoelectric coefficient d₃₃ and remnant polarization P_r can be obtained, as summarized in Fig. 4(c). d₃₃ decreases monotonically with increasing temperature, and 40% reduction of d₃₃ occurs when the temperature reaches 120 °C. For piezoelectric crystals, the intrinsic piezoelectric coefficient d₃₃ can be determined by eqn (4):^22,32

d₃₃ = 2Qε₀ε₃₃P₃ (4)

where Q is the electrostrictive constant, which barely varies with temperature;³⁴ ε₀ is the vacuum permittivity; ε₃₃ is the permittivity and in this case it does not change much in the temperature range from room temperature to 120 °C, as shown in Fig. 2(b). However, P₃ is the polarization along the polar axis and approximately equals the remnant polarization P_r for ferroelectric polycrystals, which in this case shares a similar trend with d₃₃ within the same temperature range. Thus the loss of polarization at elevated temperatures possibly due to the PPT effect may be responsible for the reduction of d₃₃. Additionally, the characteristic domain morphology at the polymorphic phase boundary gradually diminishes and the related extrinsic contribution to piezoelectric response also becomes weaker with increasing temperature.

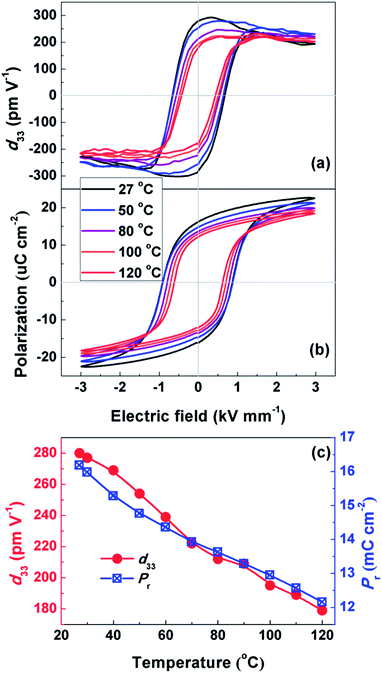Fig. 4 Temperature-dependent (a) piezoelectric coefficient d₃₃(E) hysteresis curves, (b) polarization P(E) hysteresis loops, and (c) piezoelectric coefficient d₃₃ and remnant polarization P_r.

A high piezoelectric coefficient d₃₃ is recognized as the figure of merit for electromechanical applications, e.g., sensors or ultrasonic devices; while the normalized strain d₃₃* is the key feature that matters in actuator systems.⁴ The piezoelectric strain S(E) measurement gives a d₃₃* value of 361 pm V⁻¹ at an electric field of 4 kV mm⁻¹ (see Table 1). It is interesting to note that the normalized strain d₃₃* is much larger than the piezoelectric coefficient d₃₃, which may originate from the constitution of the piezoelectric effect. As elucidated in the foregoing part, both intrinsic and extrinsic contributions constitute the piezoelectricity. The intrinsic contribution should be at the same level regardless of the measuring approach, while the extrinsic component is sensitive to external excitation, especially in the case of ceramics with nano-domains. For quasi-static d₃₃ meter and the field-dependent piezoelectric coefficient d₃₃(E) measurement, low external fields (mechanical or electrical) of 0.25 N and 25 V were applied, respectively. However, the piezoelectric strain S(E) measurement was done under an electric field well-above the coercive field E_C. The higher extrinsic contribution from domain wall movement to the response of piezoelectric strain S(E) measurement may be the origin of the much larger normalized strain d₃₃* over the piezoelectric coefficient d₃₃. Furthermore, the electric-field-induced domain switching in piezoelectric strain S(E) measurement could be the additional income of strain.

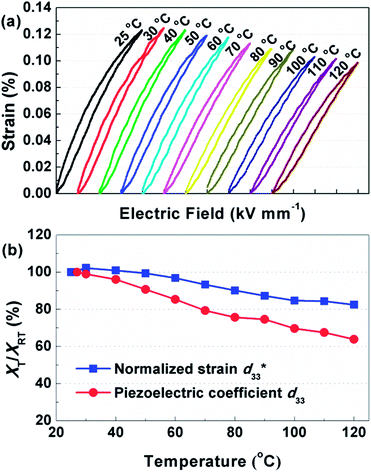
Though the KNNLTS ceramics exhibit high piezoelectricity including both piezoelectric coefficient d₃₃ and normalized strain d₃₃* at room temperature, a temperature-insensitive strain behavior is indispensable to secure successful implementation of the material in actuator systems.^19,22 In this work, temperature-dependent d₃₃* of KNNLTS ceramics were also reported. The temperature dependence of unipolar S–E curves and corresponding d₃₃* values are presented in Fig. 5. The d₃₃* peaks around a temperature of 30 °C, and the variation is within 18% over the whole temperature range. An intriguing phenomenon was observed that the normalized strain d₃₃* possesses better temperature stability in comparison with that of the small signal piezoelectric coefficient d₃₃. These phenomena are in accordance with our previous investigations on CaZrO₃-modified (K,Na,Li)(Nb,Ta)O₃ ceramics,³⁵ thus they are possibly independent of the nature of the composition. Although it is well known that an electric field can induce a phase transition from paraelectric to ferroelectric phase,^36,37 less attention has been paid to the analogous phenomenon between two ferroelectric phases. It is speculated that the electric field induced phase transition could be one of the possible causes for the superior temperature stability of normalized strain d₃₃* over piezoelectric coefficient d₃₃. Moreover, the outcomes can also be interpreted from the perspective of electric-field-engineered domain configuration. For BaTiO₃ single crystals, the stimulation of electric field facilitates the formation of fine domain structures even at a temperature above T_C.²⁷ The engineered domain morphology remains stable below T_C, and it was believed to be the main cause of significantly enhanced piezoelectric properties. In contrast to the fading domain morphology at high temperatures during the measurement of d₃₃, the piezoelectric strain S(E) measurement is accompanied by maintaining the featured domain configuration with the aid of electric field when approaching high temperature. Determined by the additional extrinsic contribution from domain configuration, normalized strain d₃₃* commits better thermal resistance than piezoelectric coefficient d₃₃. In addition, it should be mentioned that the current system exhibits inferior temperature stability of strain behavior to the CaZrO₃-modified (K,Na,Li)(Nb,Ta)O₃ (especially the one with 5 mol% CaZrO₃, abbreviated as CZ5).²² It was suggested that the phase structure plays a primary role in CZ5 ceramics, which are endowed with a diminished difference between orthorhombic and tetragonal phases as manifested by the reduced c/a ratio.²² In contrast, a distinct phase evolution process still exists in KNNLTS ceramics, which may account for the inferior temperature stability of strain behavior.

Fig. 5 (a) Unipolar piezoelectric strain S(E) curves at various temperatures and (b) temperature stability of normalized strain d₃₃*. The data for piezoelectric coefficient d₃₃ is provided for comparison.

Besides, the effect of stress on the piezoelectric performance, including the piezoelectric coefficient d₃₃ and normalized strain d₃₃*, is important for the applications of piezoceramics. It was reported that piezoelectric coefficient d₃₃ is barely affected by the hydrostatic pressure in niobate single crystals,³⁸ while the d₃₃ of PZT ceramics was shown to be sensitive to external stress.³⁹ In the case of normalized strain d₃₃*, it is better to use the terminology of blocking stress, which means the maximum stress an actuator can generate against an infinitely stiff external clamping.⁴ The literature indicates that the lead-free systems could generate comparable blocking fore with PZT ceramics.⁴

4 Conclusions

In summary, the domain morphology and temperature-dependent piezoelectricity of (K,Na,Li)(Nb,Ta,Sb)O₃ (KNNLTS) lead-free piezoceramics at the polymorphic phase boundary were investigated. The joint effects of polymorphic phase transition and nano-domain contribution were identified to be the origin of the superior piezoelectric performance in the system. Besides, the novel and facile method based on the field-dependent piezoelectric coefficient d₃₃(E) measurement demonstrated the capability of evaluating the in situ temperature-dependent piezoelectric coefficient d₃₃, which may facilitate the development of lead-free piezoceramics.

Acknowledgements

This work was supported by National Nature Science Foundation of China (Grants no. 51332002, 51302144, 51221291, 51211140345) and the Ministry of Science and Technology of China under the Grant 2009CB623304.

Notes and references

1. K. Uchino, in Ferroelectric Devices, Marcel Dekker, New York, 2000.
2. J. Rödel, W. Jo, K. T. P. Seifert, E.-M. Anton, T. Granzow and D. Damjanovic, J. Am. Ceram. Soc., 2009, 92, 1153.
3. T. R. Shrout and S. J. Zhang, J. Electroceram., 2007, 19, 113.
4. W. Jo, R. Dittmer, M. Acosta, J. Zang, C. Groh, E. Sapper, K. Wang and J. Rödel, J. Electroceram., 2012, 29, 71.
5. J. Varghese, R. W. Whatmore and J. D. Holmes, J. Mater. Chem. C, 2013, 1, 2618.
6. J.-F. Li, K. Wang, F.-Y. Zhu, L.-Q. Cheng and F.-Z. Yao, J. Am. Ceram. Soc., 2013, 96, 3677.
7. D. Maurya, Y. Zhou, Y. Yan and S. Priya, J. Mater. Chem. C, 2013, 1, 2102.
8. Y. Saito, H. Takao, T. Tani, T. Nonoyama, K. Takatori, T. Homma, T. Nagaya and M. Nakamura, Nature, 2004, 432, 84.
9. R. Zuo and J. Fu, J. Am. Ceram. Soc., 2011, 94, 1467.
10. S. Y. Choi, S.-J. Jeong, D.-S. Lee, M.-S. Kim, J.-S. Lee, J.-H. Cho, B. Kim and Y. Ikuhara, Chem. Mater., 2012, 24, 3363.
11. K. Wang and J.-F. Li, Adv. Funct. Mater., 2010, 20, 1924.
12. J. Yao, J. Li, D. Viehland, Y. Chang and G. L. Messing, Appl. Phys. Lett., 2012, 100, 132902.
13. Y. Dai, X. Zhang and G. Zhou, Appl. Phys. Lett., 2007, 90, 262903.
14. R.-P. Herber, G. A. Schneider, S. Wagner and M. J. Hoffmann, Appl. Phys. Lett., 2007, 90, 252905.
15. J. Fu, R. Zuo and Z. Xu, Appl. Phys. Lett., 2011, 99, 062901.
16. K. A. Schönau, L. A. Schmitt, M. Knapp, H. Fuess, R.-A. Eichel, H. Kungl and M. J. Hoffmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 184117.
17. J. Yao, L. Yan, W. Ge, L. Luo, J. Li, D. Viehland, Q. Zhang and H. Luo, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 054107.
18. F. Rubio-Marcos, A. Del Campo, R. López-Juárez, J. J. Romero and J. F. Fernández, J. Mater. Chem., 2012, 22, 9714.
19. S. Zhang, R. Xia, H. Hao, H. Liu and T. R. Shrout, Appl. Phys. Lett., 2008, 92, 152904.
20. E. Hollenstein, M. Davis, D. Damjanovic and N. Setter, Appl. Phys. Lett., 2005, 87, 182905.
21. F.-Z. Yao, K. Wang and J.-F. Li, J. Appl. Phys., 2013, 113, 174105.
22. K. Wang, F.-Z. Yao, W. Jo, D. Gobeljic, V. V. Shvartsman, D. C. Lupascu, J.-F. Li and J. Rödel, Adv. Funct. Mater., 2013, 23, 4079.
23. X. Cheng, J. Wu, X. Wang, B. Zhang, J. Zhu, D. Xiao, X. Wang, X. Lou and W. Liang, J. Appl. Phys., 2013, 114, 124107.
24. J. Wu, D. Xiao, Y. Wang, W. Wu, B. Zhang and J. Zhu, J. Appl. Phys., 2008, 104, 024102.
25. L. Burianova, M. Sulc and M. Prokopova, J. Eur. Ceram. Soc., 2001, 21, 1387.
26. K. Wang and J.-F. Li, Appl. Phys. Lett., 2007, 91, 262902.
27. S. Wada, K. Yako, H. Kakemoto, T. Tsurumi and T. Kiguchi, J. Appl. Phys., 2005, 98, 014109.
28. D.-T. Le, S.-J. Kwon, N.-R. Yeom, Y.-J. Lee, Y.-H. Jeong, M.-P. Chun, J.-H. Nam, J.-H. Paik, B.-I. Kim, J.-H. Cho and N. Alford, J. Am. Ceram. Soc., 2013, 96, 174.
29. S. Zhang, H. J. Lee, C. Ma, X. Tan and A. Fetiera, J. Am. Ceram. Soc., 2011, 94, 3659.
30. J. Gao, D. Xue, Y. Wang, D. Wang, L. Zhang, H. Wu, S. Guo, H. Bao, C. Zhou, W. Liu, S. Hou, G. Xiao and X. Ren, Appl. Phys. Lett., 2011, 99, 092901.
31. G. A. Rossetti, A. G. Khachaturyan, G. Akcay and Y. Ni, J. Appl. Phys., 2008, 103, 114113.
32. D. Damjanovic, J. Am. Ceram. Soc., 2005, 88, 2663.
33. J. Fialka and P. Beneš, IEEE Trans. Instrum. Meas., 2013, 62, 1047.
34. J. Kuwata, K. Uchino and S. Nomura, Jpn. J. Appl. Phys., 1980, 19, 2099.
35. F.-Z. Yao, K. Wang and J.-F. Li, et al., submitted.
36. M. E. Caspari and W. J. Merz, Phys. Rev., 1950, 80, 1082–1089.
37. D. Meyerhofer, Phys. Rev. B: Solid State, 1958, 112, 413–423.
38. L. Liang, Y. L. Li, F. Xue and L.-Q. Chen, J. Appl. Phys., 2012, 112, 064106.
39. D. Damjanovic, J. Appl. Phys., 1997, 82, 1788.

---