Open Access Article
Open Access ArticleMolecular dynamics of itraconazole confined in thin supported layers
Emmanuel Urandu Mapesa*a,
Magdalena Tarnackabc,
Ewa Kamińskad,
Karolina Adrjanowicze,
Mateusz Dulskibc,
Wilhelm Kossacka,
Martin Tressa,
Wycliffe Kiprop Kipnusua,
Kamil Kamińskibc and
Friedrich Kremera
aInstitute for Experimental Physics I, University of Leipzig, Linnestr. 5, 04103, Leipzig, Germany. E-mail: urandu@physik.uni-leipzig.de
bInstitute of Physics, University of Silesia, ul. Uniwersytecka 4, 40-007 Katowice, Poland
cSilesian Center of Education and Interdisciplinary Research, University of Silesia, 75 Pulku Piechoty 1A, 41-500 Chorzów, Poland
dDepartment of Pharmacognosy and Phytochemistry, School of Pharmacy and Division of Laboratory Medicine in Sosnowiec, Medical University of Silesia in Katowice, ul. Jagiellonska 4, 41-200 Sosnowiec, Poland
eNanoBioMedical Centre, Adam Mickiewicz University, Umultowska 85, 61-614 Poznan, Poland
First published on 18th June 2014
Abstract
Broadband Dielectric Spectroscopy (BDS) is used to study the molecular dynamics of thin layers of itraconazole – an active pharmaceutical ingredient with rod-like structure and whose Differential Scanning Calorimetry (DSC) scans reveal liquid crystalline-like phase transitions. It is found that (i) the structural relaxation process remains bulk like, within the limits of experimental accuracy, in its mean relaxation rate, while (ii) its shape is governed by two competing events: interfacial interactions, and crystalline ordering. Additionally, (iii) the dynamics of the δ-relaxation – assigned to the flip–flop rotation of the molecule about its short axis – deviates from bulk behaviour as the glass transition is approached for the confined material. These observations are rationalized within the framework of molecular dynamics as currently understood.
1 Introduction
To a large extent, the bulk (static and dynamic) properties of low-molecular weight and polymeric materials are well known. In many actual applications (e.g. photoresists, batteries, sensors for smart drug delivery, etc.) however, the glass formers are confined; they are used in diminished dimensions for purposes of increasing performance and convenience. Consequently, they have – due to an increased surface area to volume ratio – a large fraction of molecules or segments near an interface. How specific aspects of this confinement influence overall properties of the system is a prevailing subject of current soft matter research. To this end, a number of experimental techniques (e.g. Ellipsometry,1,2 X-ray reflectivity,3 thermal expansion spectroscopy,4 positron annihilation lifetime spectroscopy,5 AC-chip Calorimetry,6 Broadband Dielectric Spectroscopy2,5,7–10) have been employed to study key parameters (such as molecular weight,5,10 tacticity,11 measurement ambient,12,13 nature of substrate surface,2,3,14 concentration of mother solutions9 and even the type of experiment15,16) that may influence dynamics in confinement. While there are contradicting results from various research labs, it is becoming clear that techniques which probe the system in (quasi-equilibrium) liquid state have concurring results, while major variations arise when the system is investigated deep in the (non-equilibrium) glassy state.16,17Thermotropic liquid crystals (LC) are a class of matter with properties intermediate between those of the crystalline and isotropic liquid state. Liquids have maximal mobility and minimal (positional and translational) order while the reverse is true for crystals. In LCs, aspects of both states co-exist, and mesomorphic phases develop with a competing interplay between order and mobility. The most significant liquid crystalline structures are the smectic and nematic mesophases, the latter being the mesophase with the least order. In the nematic regime, molecules have all translational degrees of freedom and hence no long range positional order. Their long axes are favorably aligned with respect to a common unit vector n, the so-called nematic director. The degree of orientation18 of the molecules is described by an order parameter S, given by S = 〈3cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ − 1〉/2, where θ is the angle between the director n and the direction of the long axis of the molecule; the brackets denote statistical averaging. It is easy to see that for a fully aligned LC phase, S = 1. The aspect of mobility presents the opportunity to modify the orientations of the molecules by use of external electric (or magnetic) fields. Consequently, broadband dielectric spectroscopy is a versatile tool to study LCs. Liquid crystalline properties arise due to the anisotropy in the shape of the molecules; most of them have a rod-like unit in their structure, although bent-shaped and disc-like units in molecules are also known to give rise to liquid crystalline properties.19 Since LCs are anisotropic systems, their dielectric properties are anisotropic as well, and the complex dielectric function ε*(ω) – where ω is the angular frequency – is given by a tensor. This tensor, in the case of uniaxial nematic phases, has two components ε∥* and ε⊥* parallel and normal, respectively, to the nematic director. For a detailed discussion of the theory of dielectric relaxations in LCs, the reader is referred to other publications.20–23 Briefly described, the starting point is the fact that the molecular dipole moment vector of a mesogenic unit has two components, one oriented longitudinal and the other transverse to its long axis. The dielectric response arises from correlation functions of the polarization fluctuations parallel and normal to the nematic director. In this semi-microscopic framework, the measured dielectric function parallel ε∥*(ω) and normal ε⊥*(ω) to the director has different weighted sums of four underlying relaxation modes depending on the macroscopic orientation of the sample. The relaxation mode with the lowest frequency is due to rotational fluctuations of the molecule around its short axis, and it determines ε∥*(ω). This process is called the δ-relaxation.24–28 The remaining three relaxations – different tumbling fluctuations of the molecules about their long axis – have nearly the same relaxation rate and may form one broad relaxation process, which is related to ε⊥*(ω). This tumbling mode is located at higher frequencies than the δ process. While there has been controversy concerning which of these two processes is responsible for glassy dynamics in glass-forming LCs, recent experiments26,29 have helped identify the tumbling mode as being the underlying process. A comparison between BDS data in the present work and temperature modulated DSC data published elsewhere30 (see activation plots) confirms this finding for itraconazole. Therefore the latter process can simply be referred to as the α-process, akin to the structural relaxation process in conventional glass formers.
θ − 1〉/2, where θ is the angle between the director n and the direction of the long axis of the molecule; the brackets denote statistical averaging. It is easy to see that for a fully aligned LC phase, S = 1. The aspect of mobility presents the opportunity to modify the orientations of the molecules by use of external electric (or magnetic) fields. Consequently, broadband dielectric spectroscopy is a versatile tool to study LCs. Liquid crystalline properties arise due to the anisotropy in the shape of the molecules; most of them have a rod-like unit in their structure, although bent-shaped and disc-like units in molecules are also known to give rise to liquid crystalline properties.19 Since LCs are anisotropic systems, their dielectric properties are anisotropic as well, and the complex dielectric function ε*(ω) – where ω is the angular frequency – is given by a tensor. This tensor, in the case of uniaxial nematic phases, has two components ε∥* and ε⊥* parallel and normal, respectively, to the nematic director. For a detailed discussion of the theory of dielectric relaxations in LCs, the reader is referred to other publications.20–23 Briefly described, the starting point is the fact that the molecular dipole moment vector of a mesogenic unit has two components, one oriented longitudinal and the other transverse to its long axis. The dielectric response arises from correlation functions of the polarization fluctuations parallel and normal to the nematic director. In this semi-microscopic framework, the measured dielectric function parallel ε∥*(ω) and normal ε⊥*(ω) to the director has different weighted sums of four underlying relaxation modes depending on the macroscopic orientation of the sample. The relaxation mode with the lowest frequency is due to rotational fluctuations of the molecule around its short axis, and it determines ε∥*(ω). This process is called the δ-relaxation.24–28 The remaining three relaxations – different tumbling fluctuations of the molecules about their long axis – have nearly the same relaxation rate and may form one broad relaxation process, which is related to ε⊥*(ω). This tumbling mode is located at higher frequencies than the δ process. While there has been controversy concerning which of these two processes is responsible for glassy dynamics in glass-forming LCs, recent experiments26,29 have helped identify the tumbling mode as being the underlying process. A comparison between BDS data in the present work and temperature modulated DSC data published elsewhere30 (see activation plots) confirms this finding for itraconazole. Therefore the latter process can simply be referred to as the α-process, akin to the structural relaxation process in conventional glass formers.
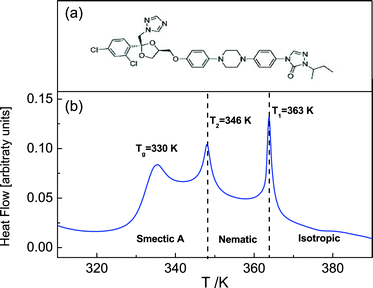
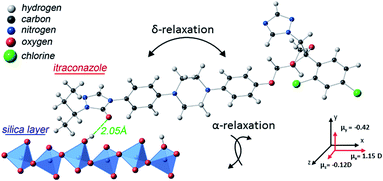
Itraconazole, the triazole derivative studied in this work, is an active pharmaceutical ingredient (API) with rod-like structure and is known to have antifungal activity.31 Two relaxation processes30 have been identified in the bulk material, i.e. the structural (α-) relaxation process, and a δ-process (at lower frequencies in the supercooled liquid) whose origin is explained in the foregoing introduction. Additionally, although a first glance at the molecule (Fig. 1a) does not reveal its liquid crystalline-like nature (absence of tail ends), DSC scans find two endothermic peaks that are recognizable as being connected to the formation of nematic and Smectic A phases.30,32,33 In the current report – using Broadband Dielectric Spectroscopy (BDS) – we follow the dynamics of itraconazole systematically confined in supported layers, down to a thickness of 6 nm.
2 Experimental
2.1 Material
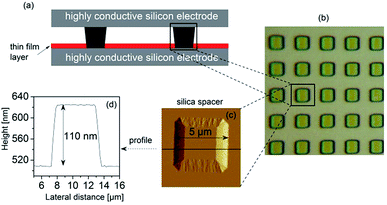
The sample material – itraconazole IUPAC name: (2R,4S)-rel-1-(butan-2-yl)-4-{4-[4-(4-{[(2R,4S)-2-(2,4-dichlorophenyl)-2-(1H-1,2,4-triazol-1-ylmethyl)-1,3-dioxolan-4-yl]methoxy}phenyl)piperazin-1-yl]phenyl}-4,5-dihydro-1H-1,2,4-triazol-5-one), molecular formula: C35H38Cl2N8O4, Mw = 705.64 g mol−1) was supplied by Sigma Aldrich with purity greater than 99%, and used without further purification. The starting material was completely crystalline with a melting point of 439 K, which agrees with what is reported in the literature (438–451 K).32 Its chemical structure is displayed in Fig. 1a.2.2 Methods
3 Results and discussion
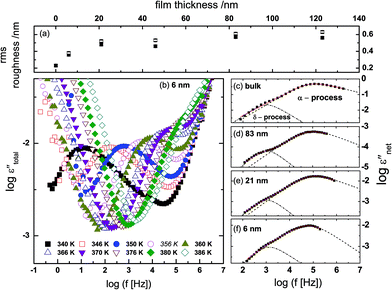
The root mean square (rms) roughness of the film surfaces was determined at room temperature by AFM for both the as-prepared and post-measured samples (i.e. after annealing and dielectric measurements). It is observed (see Fig. 3a) that (i) there's a tendency for the roughness to increase with layer thickness, but the absolute values remain below 0.7 nm (which is ∼10% of the thickness of the thinnest layer prepared) as determined from height images of size 1 nm2; and (ii) a minimal change in surface roughness (≤8%) is recorded for the post-measured samples when compared to the same sample in the as-prepared state. These findings prove stable film surfaces and exclude effects of dewetting or roughness-induced adulterations of the molecular dynamics.To analyze the isothermal spectra of the dielectric loss, two Havriliak–Negami (HN) functions42 were used:
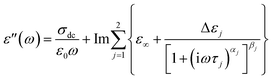 | (1) |
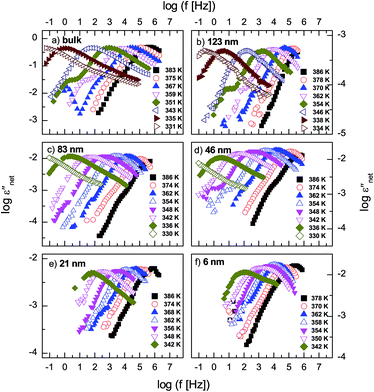
The measured dielectric response of the thin films in our set up includes some specious conductivity and resistance of the silicon electrodes which cause an increase in the dielectric loss in the low and high frequency flanks, respectively. Fig. 3b is representative data for a 6 nm thin layer, and shows the molecular processes together with the extra contributions on the low and high frequency sides. These spectra show the structural (α-) relaxation process (due to precessing motions of the molecules), which underlies the dynamic glass transition, and a shoulder between the α-process, and the conductivity contribution. This is a δ-relaxation process – whose genesis is the flip–flop fluctuation of the itraconazole molecule about its short axis – clearly resolved after subtraction of the dc conductivity (see Fig. 3c–f). In Fig. 4, all the dielectric loss spectra (after subtraction of both the conductivity contribution and the high-frequency wing) for bulk itraconazole (panel a) and films of various thickness, i.e., 123, 83, 46, 21 and 6 nm (panels b to f) are presented. As evident from Fig. 3 and 4, the two relaxation processes present in the bulk material are also exhibited by the thin layers.
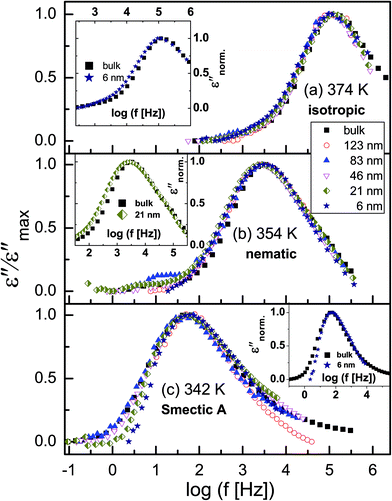
Fig. 5 shows normalized dielectric loss spectra obtained for all examined samples at 374, 354 and 342 K, that is, temperatures at which, respectively, isotropic, nematic and Smectic A mesophases are expected. In Fig. 6, the evolution of the mean relaxation rate (for the two molecular processes) with temperature, as well as the film-thickness dependence of the dielectrically-determined glass transition temperature, Tg, are presented. It is clearly observed that: (i) at a given temperature (in the nematic and isotropic phases), the structural relaxation peak is broadened (on the lower frequency side) for the thin layers when comparison is made with bulk data (insets-Fig. 5a and b); (ii) there is a tendency (in the Smectic A phase) for the α-peak to narrow down with reducing layer thickness (Fig. 5c); (iii) the mean relaxation rate of the α-process (and hence the dynamic glass transition) remains bulk-like, within the limits of experimental uncertainty, independent of the layer thickness (Fig. 6); (iv) the δ-relaxation exhibits a pronounced slowing down, for the confined molecules, as the LC is cooled towards glass formation (Fig. 6a); and (v) while it is typical of LCs to have just one relaxation process above the clearing temperature,43 itraconazole has two (Fig. 6a). Each of these observations is rationalized in the following discussion.
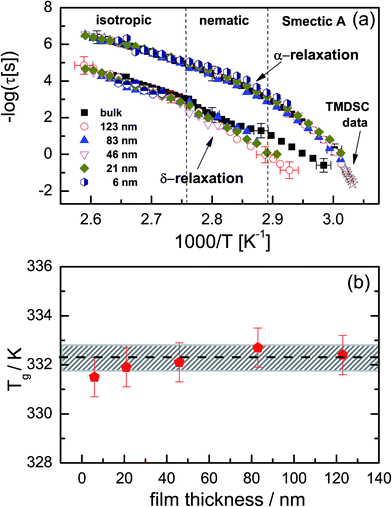 | ||
| Fig. 6 (a) The temperature-dependence of the mean relaxation times for the α- and δ-processes for different layer thicknesses. The star symbols represent temperature-modulated DSC data (reproduced from ref. 30 with permission from the PCCP Owner Societies) obtained for the bulk sample; (b) the dielectrically-determined glass transition temperature for the layers. The dashed line in (b) represents the calorimetric bulk Tg with its experimental error of ±0.5 K included (shaded region) for completeness. | ||
Concerning the broadening (at high temperatures) of the structural relaxation process with decreasing thickness, theoretical computations were performed to quantify the interaction between itraconazole and the silica substrate. It is shown (Fig. 7) that hydrogen bonds – with an average length of about 2.05 Å – are formed between oxygen and OH units belonging to, respectively, the carbonyl moiety in itraconazole and silica surface layer. These are relatively strong interactions especially when we keep in mind that, for instance, the average length of the hydrogen bond in water is ∼1.96 Å.44 It has been proven that such attractive interactions lead to immobilization45 of some of the molecules, hence introducing slower modes (which show up as a broadened peak on the long-time side).46 Given the immobilization of some molecules in contact with the substrate, it follows that upon heating through the transition, only a fraction of the liquid-crystalline material participates in the disordering. This aspect can aptly be studied by DSC on thin samples, and analyzing the intensity of the transition peaks, but due to technical reasons, this has not yet been realized.
While (attractive) interfacial interactions cause a broadening of the α-peak, crystalline ordering in the sample promotes its narrowing. These therefore are competing processes, and whichever one dominates is temperature-determined. At low temperatures, i.e., in the Smectic A phase, the peak tends to narrow down with reducing layer thickness. To understand this, it must be noted that smectic layering begins at the interface,47 and progresses through the film expanse in the direction perpendicular to the wall; the extent to which smectic ordering permeates the sample volume is therefore inversely proportional to the film thickness. Hence, the thinner the film, the more the order parameter aligns in the direction of the applied electric field.
For the structural relaxation, the temperature-dependence of the mean relaxation times plotted in Fig. 6a were fitted by the Vogel–Fulcher–Tammann (VFT) equation48–50 which reads
τ(T) = τ∞![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{(DTT0)/(T − T0)}, exp{(DTT0)/(T − T0)},
| (2) |
| Sample | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ τ |
DT | T0 | Tg ± 1 K |
|---|---|---|---|---|
| Bulk | −9.8 ± 0.1 | 635.8 ± 27.3 | 305.2 ± 0.7 | 332.5 |
| 123 nm | −10.4 ± 0.2 | 777.9 ± 49.2 | 300.5 ± 1.8 | 332.4 |
| 83 nm | −11.1 ± 0.2 | 972.0 ± 48.4 | 294.6 ± 1.3 | 332.7 |
| 46 nm | −10.2 ± 0.1 | 729.6 ± 23.9 | 301.1 ± 0.7 | 332.1 |
| 21 nm | −10.5 ± 0.1 | 801 ± 17 | 298.3 ± 0.5 | 331.9 |
| 6 nm | −10 ± 1 | 684.6 ± 296.1 | 299.8 ± 10.5 | 331.5 |
The flip–flop fluctuation of the molecule about its short axis (δ-relaxation) is, naturally, a slow process because of its coupling to the centres of mass.57 Given this fact, it follows that geometrically induced restrictions should further slowdown the movement, especially at low temperatures. Since the data in Fig. 6 does not reveal a thickness-dependence of the slowing down, we infer that the main cause of this phenomenon is the spin casting process itself. A number of studies have shown that the spin-coating procedure introduces conformational changes58,59 which have a direct consequence on the ensuing molecular dynamics.9,60–62
Finally, we turn our attention to the presence of two relaxation processes above the clearing temperature. Typically, only one relaxation process is expected in the isotropic mesophase because the liquid state dominates. The two processes registered in (bulk and confined) itraconazole, however, suggest that the molecules can still undergo distinguishable motions about their short and long axes, as would be the case in the more-ordered phases. Theoretical predictions,63 and some X-ray diffraction (XRD) experiments have hinted at the existence of nematic clusters64–67 which may not disappear68 even at high temperatures in some LCs. Consequently, local, randomly oriented nematic-ordered structures (clusters) – without long-range ordering – can be found in the isotropic liquid phase. Our dielectric results therefore provide proof of the existence of a locally ordered phase in the temperature regime where isotropism would be expected to prevail.
4 Conclusions
In this paper, the molecular dynamics of confined itraconazole were investigated and compared to the bulk material. It is shown that the mean structural relaxation times – and hence the dynamic glass transition – remain bulk-like in the accessible temperature range even for the thinnest studied sample of 6 nm. The distribution of these relaxation times is affected by two competing events: the interfacial interactions and crystalline ordering in the sample. It is also demonstrated that confinement of itraconazole in thin layers slows down the molecules' flip–flop motion (about their short axes) as the glass transition is approached from the upper side. These results provide further understanding of liquid crystal behaviour in confinement, and bear direct consequences to their applicability in nanotechnology.Acknowledgements
E.U.M and F.K are grateful for funding received from the German Research Foundation, respectively, within the Focused Research Program SPP 1369, and in the framework of the Centre for Collaborative Research (SFB-TRR 102) of the Universities of Martin-Luther (Halle-Wittenberg) and Leipzig. M.T.a appreciates financial support from the Graduate School BuildMoNa. Financial support from the Polish National Science Centre, decisions DEC-2013/09/D/NZ7/04194 and DEC-2012/05/B/ST4/00089, for E.K. and M.T.b, and K.K., respectively, is ackowledged. K.A. thanks the National Centre for Research and Development (nanomaterials and their potential application in nanobiomedicine) for grants. This research was also financed by the Medical University of Silesia as part of Research for Young Scientists (Contract No. KNW-2-004/N/4/N). Support from the PL-Grid Infrastructure is also appreciated. We thank Gladys Mumbua for fruitful discussions.References
- J. L. Keddie, R. A. L. Jones and R. A. Cory, Europhys. Lett., 1994, 27, 59–64 CrossRef CAS.
- M. Erber, M. Tress, E. U. Mapesa, A. Serghei, K.-J. Eichhorn, B. Voit and F. Kremer, Macromolecules, 2010, 43, 7729–7733 CrossRef CAS.
- G. Reiter, Macromolecules, 1994, 27, 3046–3052 CrossRef CAS.
- K. Fukao and Y. Miyamoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 011803 CrossRef CAS.
- G. B. DeMaggio, W. E. Frieze, D. W. Gidley, M. Zhu, H. A. Hristov and A. F. Yee, Phys. Rev. Lett., 1997, 78, 1524–1527 CrossRef CAS.
- H. Huth, A. A. Minakov and C. Schick, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 2996–3005 CrossRef CAS.
- F. Kremer, A. Serghei, J. R. Sangoro, M. Tress and E. U. Mapesa, IEEE Trans. Dielectr. Electr. Insul., 2009 DOI:10.1109/CEIDP.2009.5377717.
- E. U. Mapesa, M. Erber, M. Tress, K.-J. Eichhorn, A. Serghei, B. Voit and F. Kremer, Eur. Phys. J.: Spec. Top., 2010, 189, 173–180 CrossRef CAS.
- E. U. Mapesa, M. Tress, G. Schulz, H. Huth, C. Schick, M. Reiche and F. Kremer, Soft Matter, 2013, 9, 10592–10598 RSC.
- M. Tress, M. Erber, E. U. Mapesa, H. Huth, J. Müller, A. Serghei, C. Schick, K.-J. Eichhorn, B. Voit and F. Kremer, Macromolecules, 2010, 43, 9937–9944 CrossRef CAS.
- Y. Grohens, L. Hamon, G. Reiter, A. Soldera and Y. Holl, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 8, 217–224 CrossRef CAS PubMed.
- A. Serghei, H. Huth, M. Schellenberger, C. Schick and F. Kremer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061801 CrossRef CAS.
- A. N. Raegen, M. V. Massa, J. A. Forrest and K. Dalnoki-Veress, Eur. Phys. J. E: Soft Matter Biol. Phys., 2008, 27, 375–377 CrossRef CAS PubMed.
- J. A. Forrest, K. Dalnoki-Veress, J. R. Stevens and J. R. Dutcher, Phys. Rev. Lett., 1996, 77, 2002–2005 CrossRef CAS.
- O. Bäumchen, J. D. McGraw, J. A. Forrest and K. Dalnoki-Veress, Phys. Rev. Lett., 2012, 109, 055701 CrossRef.
- V. M. Boucher, D. Cangialosi, H. Yin, A. Schönhals, A. Alegría and J. Colmenero, Soft Matter, 2012, 8, 5119–5122 RSC.
- F. Kremer, E. U. Mapesa, M. Tress, and M. Reiche, in Recent Advances in Broadband Dielectric Spectroscopy, ed. Y. P. Kalmykov, Springer, Dordrecht, 2011, pp. 163–178 Search PubMed.
- S. Chandrasekhar, Liquid Crystals, Cambridge University Press, Cambridge, 2nd edn, 1992 Search PubMed.
- Handbook of liquid crystals, ed. D. Demus, J. Goodby, G. W. Gray, H. W. Spiess and V. Vill, Wiley-VCH, Weinheim, 1998 Search PubMed.
- P. Luigi Nordio, G. Rigatti and U. Segre, Mol. Phys., 1973, 25, 129–136 CrossRef.
- G. S. Attard, K. Araki and G. Williams, Br. Polym. J., 1987, 19, 119–127 CrossRef CAS.
- K. Araki, G. S. Attard, A. Kozak, G. Williams, G. W. Gray, D. Lacey and G. Nestor, J. Chem. Soc., Faraday Trans. 2, 1988, 84, 1067–1081 RSC.
- Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schönhals, Springer-Verlag, Berlin, 2003 Search PubMed.
- W. H. de Jeu, Physical properties of liquid crystalline material, Gordon & Breach, New York, London, Paris, 1979 Search PubMed.
- C. Baehr, B. Glüsen, J. H. Wendorff and E. G. Staring, Macromol. Rapid Commun., 1994, 15, 327–333 CrossRef CAS.
- A. Brás, M. Dionísio, H. Huth, C. Schick and A. Schönhals, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 061708 CrossRef.
- A. R. Brás, S. Frunza, L. Guerreiro, I. M. Fonseca, A. Corma, L. Frunza, M. Dionísio and A. Schönhals, J. Chem. Phys., 2010, 132, 224508 CrossRef PubMed.
- C. Grigoriadis, H. Duran, M. Steinhart, M. Kappl, H.-J. Butt and G. Floudas, ACS Nano, 2011, 5, 9208–9215 CrossRef CAS PubMed.
- C. Schick, D. Sukhorukov and A. Schönhals, Macromol. Chem. Phys., 2001, 202, 1398–1404 CrossRef CAS.
- M. Tarnacka, K. Adrjanowicz, E. Kaminska, K. Kaminski, K. Grzybowska, K. Kolodziejczyk, P. Wlodarczyk, L. Hawelek, G. Garbacz, A. Kocot and M. Paluch, Phys. Chem. Chem. Phys., 2013, 15, 20742 RSC.
- J. Van Cutsem, F. Van Gerven, M. A. Van de Ven, M. Borgers and P. A. Janssen, Antimicrob. Agents Chemother., 1984, 26, 527–534 CrossRef CAS.
- K. Six, G. Verreck, J. Peeters, K. Binnemans, H. Berghmans, P. Augustijns, R. Kinget and G. Van den Mooter, Thermochim. Acta, 2001, 376, 175–181 CrossRef CAS.
- K. Six, G. Verreck, J. Peeters, P. Augustijns, R. Kinget and G. Van den Mooter, Int. J. Pharm., 2001, 213, 163–173 CrossRef CAS.
- A. Serghei and F. Kremer, Rev. Sci. Instrum., 2008, 79, 026101 CrossRef CAS PubMed.
- F. Kremer, M. Tress and E. U. Mapesa, Dielectrics Newsletter, 2012, 10, 1–3 Search PubMed.
- A. Serghei, M. Tress and F. Kremer, J. Chem. Phys., 2009, 131, 154904 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048 CrossRef CAS.
- S. Havriliak and S. Negami, Polymer, 1967, 8, 161–210 CrossRef CAS.
- M. Davies, R. Moutran, A. H. Price, M. S. Beevers and G. Williams, J. Chem. Soc., Faraday Trans. 2, 1976, 72, 1447–1458 RSC.
- A. C. Legon and D. J. Millen, Chem. Soc. Rev., 1987, 16, 467–498 RSC.
- S. Napolitano and M. Wübbenhorst, Nat. Commun., 2011, 2, 260–267 CrossRef.
- M. Tress, E. U. Mapesa, W. Kossack, W. K. Kipnusu, M. Reiche and F. Kremer, Science, 2013, 341, 1371–1374 CrossRef CAS PubMed.
- J. T. Mang, K. Sakamoto and S. Kumar, Mol. Cryst. Liq. Cryst., 1992, 223, 133–142 CrossRef CAS.
- H. Vogel, Phys. Z., 1921, 22, 645–646 CAS.
- G. S. Fulcher, J. Am. Ceram. Soc., 1925, 8, 339–355 CrossRef CAS PubMed.
- G. Tammann and G. Hesse, Z. Anorg. Allg. Chem., 1926, 156, 245–257 CrossRef.
- F. Kremer, A. Huwe, M. Arndt, P. Behrens and W. Schwieger, J. Phys.: Condens. Matter, 1999, 11, A175–A188 CrossRef CAS.
- I. Bahar, B. Erman, F. Kremer and E. W. Fischer, Macromolecules, 1992, 25, 816–825 CrossRef CAS.
- E. Donth, H. Huth and M. Beiner, J. Phys.: Condens. Matter, 2001, 13, L451–L462 CrossRef CAS.
- A. Schönhals, H. Goering, C. Schick, B. Frick and R. Zorn, Colloid Polym. Sci., 2004, 282, 882–891 Search PubMed.
- L. Berthier, Science, 2005, 310, 1797–1800 CrossRef CAS PubMed.
- E.-J. Donth, J. Non-Cryst. Solids, 1982, 53, 325–330 CrossRef CAS.
- C. M. Roland, Soft Matter, 2008, 4, 2316 RSC.
- A. Brûlet, F. Boué, A. Menelle and J. P. Cotton, Macromolecules, 2000, 33, 997–1001 CrossRef.
- H. Tsuruta, Y. Fujii, N. Kai, H. Kataoka, T. Ishizone, M. Doi, H. Morita and K. Tanaka, Macromolecules, 2012, 45, 4643–4649 CrossRef CAS.
- A. Serghei and F. Kremer, Phys. Rev. Lett., 2003, 91, 165702 CrossRef CAS.
- A. Serghei, F. Kremer and W. Kob, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 12, 143–146 CrossRef CAS PubMed.
- M. Solar, E. U. Mapesa, F. Kremer, K. Binder and W. Paul, EPL, 2013, 104, 66004 CrossRef.
- L. V. Azároff, Proc. Natl. Acad. Sci. U. S. A., 1980, 77, 1252–1254 CrossRef.
- I. G. Chistyakov and W. M. Chaikowsky, Mol. Cryst., 1969, 7, 269–277 CrossRef CAS.
- A. D. Vries, Mol. Cryst. Liq. Cryst., 1970, 10, 31–35 CrossRef.
- O. Francescangeli and E. T. Samulski, Soft Matter, 2010, 6, 2413 RSC.
- C. Keith, A. Lehmann, U. Baumeister, M. Prehm and C. Tschierske, Soft Matter, 2010, 6, 1704 RSC.
- A. D. Vries, Mol. Cryst. Liq. Cryst., 1970, 10, 219–236 CrossRef.
| This journal is © The Royal Society of Chemistry 2014 |