Co₉S₈ nanoflakes on graphene (Co₉S₈/G) nanocomposites for high performance supercapacitors

Abstract

Co₉S₈/graphene nanocomposites (Co₉S₈/G) at various concentrations of graphene and Co₉S₈ were prepared by a simple chemical route from cobalt nitrate and graphene as precursors in the presence of PVP as surfactant and thioacetamide (TAA) as sulfur source. To gain knowledge about the structural, morphological and physical properties, the composite material was analyzed by X-ray diffraction (XRD), Field Emission Scanning Electron Microscopy (FE-SEM), X-ray photoelectron spectroscopy (XPS) and thermogravimetric Analysis (TGA). SEM measurements showed the presence of well dispersed, ∼300 nm sized Co₉S₈ nanoflakes. To assess the properties of the nanocomposites for their applicability in supercapacitors, electrochemical analysis was carried out in 6 M KOH electrolyte. A maximum specific capacitance of 808 F g⁻¹ was observed for Co₉S₈/G-d at 5 mV s⁻¹ scan rate. Galvanostatic charge–discharge curves showed the excellent cyclic stability of Co₉S₈/G-d composite with higher charge–discharge duration than pure Co₉S₈. The excellent electrochemical performance of the composite could be due to the better electrical conductivity behavior of graphene on Co₉S₈ nanoflakes.

---

Introduction

Supercapacitors also known as ultracapacitors are energy storage devices that combine the high power density and high energy storage capability of batteries and conventional capacitors and have long cyclic life and fast dynamic charge propagation.^1,2 In general, supercapacitors fall into two categories, viz. Electric Double Layer Capacitors (EDLC) and pseudocapacitors. In EDLC energy is stored through charge accumulation at electrode and electrolyte interface whereas, the energy is stored through the surface faradic redox reactions in pseudocapacitors.³ Currently, three types of electrode materials have been used as supercapacitor electrodes; first carbon based materials like activated carbon, carbon nanotube, carbon aerogel; second conducting polymers like polyaniline and polypyrrole and finally metal oxides and hydroxides such as RuO₂, MnO₂, Co(OH)₂, NiO, ZnO, etc. In general, carbon based materials have been used in EDLC due to their high specific surface area and easy processability. But they provide relatively low specific capacitance (100–300 F g⁻¹).¹ Though metal oxides give higher specific capacitance (>2000 F g⁻¹), they are limited by their high cost and poor conductivity. Many of the metal oxides like MnO₂, Fe₂O₃, NiO, though they have high theoretical capacitance and low cost, the electrical conductivity of these metal oxides limits their power density and cycling stability. Among the transition metal oxides, RuO₂ exhibits high specific capacitive performance, but due to its high cost and toxicity, its utility is limited and cannot be commercialized. To achieve high specific capacitance and high power density with low cost, a plethora of interest has been paid to the combined usage of carbon based materials with metal oxides or polymers.⁴ Graphene, the parent of all graphitic structures, offers high specific surface area, high conductivity and outstanding mechanical properties. These factors make graphene a promising electrode material for supercapacitors. Recently graphene based metal oxide and polymer composites like G-MnO₂,⁵ G-Co₃O₄,⁶ G-NiO,⁷ RGO-CuO,⁸ G-SnO₂,⁹ G-V₂O₅,¹⁰ G-PANI¹¹ and G-PPY¹² have shown an enhanced specific capacitance than their individual forms due to the synergistic effect between the composite materials.¹³ Similar to metal oxides, metal sulfide based active electrode materials are also of tremendous interest for energy storage applications. Among the various transition metal chalcogenides, cobalt sulfide is a material of immense interest. Cobalt sulfides exist in different stoichiometric ratios like Co_1−xS, CoS, CoS₂, Co₉S₈ and Co₃S₄. ZnS and CoS electrodes have been studied for Li ion batteries and supercapacitor applications.^14,15 A maximum specific capacitance of 508 F g⁻¹ for CoS¹⁶ and 200 F g⁻¹ for ZnS¹⁴ has been reported. Although cobalt sulfide has higher thermal conductivity and electrical conductivity than other metal sulfides, it has a number of drawbacks like capacity fading, low conductivity and poor cyclability, which will result in the decay of the specific capacity and the formation of polysulfide anions.¹⁷ In this view, to resolve this, graphene was used as a conducting matrix where the presence of graphene not only increased the electrical conductivity but also improves the contact between electrode and electrolyte due to its large surface area.¹⁸ More recently, a high specific capacitance of 1535 F g⁻¹ for CoS-graphene composite was reported.¹⁹ Recently we have reported the role of N doped graphene based Co₃S₄ for supercapacitor applications.²⁰

In the current report, the electrochemical testing and supercapacitive property of Co₉S₈-graphene nanocomposites are investigated. The nanocomposites were prepared by a simple chemical method from cobalt nitrate, thioacetamide and poly (N-vinylpyrrolidone) (PVP) with different loadings of graphene. To understand the effect of Co₉S₈ and graphene, the nanocomposites were synthesized at various loadings of Co₉S₈ and graphene material and a systematic investigation has been done to optimize a particular ratio. The fabricated electrodes have been studied by cyclic voltammetry and charge–discharge technique. Results show a good capacitive behavior of 808 F g⁻¹ with good reversible charge–discharge behavior.

Experiment method

Materials

AR grade of cobalt nitrate hexahydrate (Co(NO₃)₂·6H₂O) sodium nitrate (NaNO₃), potassium permanganate (KMnO₄), sulfuric acid (H₂SO₄, 99%), sodium borohydride (NaBH₄), hydrogen peroxide (H₂O₂, 30%), sodium hydroxide (NaOH), potassium hydroxide (KOH), poly(N-vinylpyrrolidone) (C₆H₉NO)_n and thioacetamide (C₂H₅NS) were purchased from Sigma-Aldrich. All the solutions were prepared by using Milli-Q water (pH 7.2).

Preparation of graphene oxide (GO)

Graphene oxide was prepared through modified Hummer's method according to the previous literature.²¹ Graphite powder (0.5 g) and sodium nitrate (0.5 g) was mixed with 23 ml of concentrated sulfuric acid (98% pure) under stirring in an ice bath. After four hours, potassium permanganate (3 g) was added into the mixture. The reaction mixture was maintained at 35 °C for two hours with continuous stirring in water bath, which was later diluted with 46 ml of water. After that the temperature was raised to 98 °C and maintained for two hours. Then the reaction mixture was diluted with 100 ml warm water and 10 ml hydrogen peroxide under stirring. After 1 hour, the solution turned light yellow in color. The powders were collected after repeated washing in deionized water by centrifugation and the collected powder was dried at 60 °C for 24 h.

Preparation of graphene

Graphene was synthesized using sodium borohydride as a reducing agent.²¹ Initially, GO (40 mg) and water (40 ml) was ultrasonicated for 1 hour. Then, this GO dispersed water was taken in an airtight container (60 ml capacity). To it was added sodium borohydride (0.24 g) and 5 ml of 1 M sodium hydroxide solution. The mixture was kept at 90 °C for 1 hour. After cooled room temperature, the powder was separated by centrifuging at 7500 rpm. Finally the powder was dried at 60 °C for 24 h.

Preparation of Co₉S₈ nanoflakes/graphene (Co₉S₈/G) nanocomposites

Co₉S₈/G nanocomposites were prepared according to the literature with a slight modification.²² Typically Co(NO₃)₂·6H₂O (0.04 M), thioacetamide (0.06 M) and PVP (0.01 M) were added to 3 wt% of graphene in 40 ml of ultra-pure water. After the addition of NaOH (9.6 ml, 0.5 M), the solution was heated in an oil bath at 100 °C for 1 h. The color of the mixture became black indicating the formation of Co₉S₈/G nanocomposite. The solution was then sonicated for 1 h, centrifuged and washed several times with ethanol. The final powder was dried at 60 °C for 12 h. The powder was named as Co₉S₈/G-a. Similarly, other nanocomposites viz. Co₉S₈/G-b, Co₉S₈/G-c, Co₉S₈/G-d and Co₉S₈/G-e were synthesized by a similar method where a-e represents 3, 5, 7, 9, and 11 wt% of graphene loading. To know the effect of Co₉S₈ on the electrochemical activity, the synthesis was repeated at three different cobalt concentration of 0.03 M, 0.04 M and 0.05 M Co(NO₃)₂·6H₂O keeping 9 wt% graphene loading constant. The samples were named as Co₉S₈/G-x, Co₉S₈/G-y and Co₉S₈/G-z. Here Co₉S₈/G-d and Co₉S₈/G-y are the same composite i.e. Co₉S₈ prepared from 0.04 M and 9 wt% graphene loading. Pure Co₉S₈ was prepared by the above procedure without graphene.

Materials characterization

X-ray diffraction system (BRUKER, D8 Advance, Germany) was used for the X-ray analysis with Cu-Kα radiation (λ = 1.540 Å). Step scanning was done with 2θ intervals from 10° to 65°. Fourier transform infrared spectra were recorded using Spectrum one: FTIR-spectrometer in the range 450–4500 cm⁻¹ to characterize the functional groups of the composites. UV-Vis spectroscopy (JASCO, V-670 spectrometer) was used for further studying the electronic structure and optical properties of the samples. Thermogravimetric analyses (TGA) of the samples were performed in air atmosphere with SDT Q600 (TA Instruments, Korea). X-ray photoelectron spectroscopy (XPS) measurements were carried out by using a Thermo Scientific Multilab 2000 spectrometer with Mg source. The surface morphologies and EDX mappings of the composites were obtained with FESEM by using a Hitachi S-4800 and EDS respectively. The AFM images were taken from the system (Nanosurf EasyScan 2 AFM, version 1.3).

Electrical conductivity measurements

Electrical conductivity of pure Co₉S₈ and Co₉S₈/G-d composite was measured using Four Probe Set up (Model-DFP 02) at different temperatures. The active material was pelletized with the thickness of 0.45 mm and radius 6.25 mm.

Electrochemical measurements

All the electrochemical measurements were carried out with an electrochemical analyzer (CHI 600C work station, version 5.01) using a three electrode system in 6 M KOH as electrolyte solution under ambient conditions. The potentials and current were measured with respect to Ag/AgCl (sat. KCl) as the reference. Carbon paper (purchased from Cabot, USA) and Pt wire were used as the working and counter electrode respectively. The cyclic voltammetry measurements were performed at various scan rates in the potential range from −0.1 to 0.3 V. The working electrode was prepared as follows: in brief, a known amount of active material was dispersed in 5 wt% of nafion and the mixture was coated on carbon paper (3 cm × 1 cm × 0.1 cm). The total surface of active material coated area was 0.5 cm × 0.5 cm. The mass of the active material on electrode was 2 mg cm⁻². Then, the electrode was dried for 3 h at room temperature.

Results and discussion

Formation mechanism

The formation mechanism of Co₉S₈ is given as Scheme 1.²³ During the synthesis of the nanocomposites, cobalt nitrate and thioacetamide in the presence of PVP gave a brown color suspension initially and after the addition of NaOH, the color of the suspension turned aquamarine due to the reaction of Co²⁺ ions with OH⁻ to form Co(OH)₂. Later, S²⁻ ions obtained from thioacetamide decomposition at 100 °C react with the formed Co(OH)₂ to form Co₉S₈ nanoflakes on graphene sheets via noncovalent π–π interaction between delocalized π electrons of graphene and Co₉S₈.²⁴ The formation reaction is as follows,¹⁶

Co²⁺ + 2OH⁻ → Co(OH)₂ [aquamarine color]

Co(OH)₂ + S²⁻ + G → Co₉S₈/G [black color] + 2OH⁻

Scheme 1 Schematic diagram of (a) Co₉S₈/G nanocomposite formation with experimental photographic images and (b) Co₉S₈ formation mechanism.

A schematic diagram of the formation mechanism and color changes during the course of the reaction is given in Scheme 1.

Microstructural characterization

The structure and phase of the samples were identified by X-ray diffraction and the corresponding pattern of Co₉S₈/G nanocomposites and pure Co₉S₈ is shown in Fig. 1. As seen in Fig. 1a, the diffraction peaks of pure Co₉S₈ were observed at 20.2, 22.4, 32.2, 37.8, 45.2, 51.7 and 57.1° and can be indexed (111), (200), (220), (311), (400), (420) and (422) of cubic phase nature with lattice constant of 9.93 Å as in agreement with the JCPDS card no 19-0364.

Fig. 1 XRD pattern of Co₉S₈/G composite at different concentrations of graphene (a) pure Co₉S₈ (b) Co₉S₈/G-a (c) Co₉S₈/G-b (d) Co₉S₈/G-c (e) Co₉S₈/G-d (f) Co₉S₈/G-e.

Apart from the Co₉S₈ peaks, other cobalt sulfide complex phases like CoS, CoS₂ and Co₃S₄ were observed, suggesting that the cobalt sulphides are mixed phases of Co₉S₈, CoS₂, CoS and Co₃S₄ respectively. This fact was supported by Wang et al. where it has been suggested that it was difficult to obtain pure phase of cobalt sulphide because of the complex stoichiometric of cobalt chalcogenides.²⁵ Though, the other phases are mixed in Co₉S₈, the major phases corresponds to Co₉S₈. In Co₉S₈/G nanocomposite, the peak at 24.9° clearly shows the crystal plane (002) of graphene sheets²⁶ in the composite. All the diffraction peaks are sharp indicating that the high crystallinity of Co₉S₈ in Co₉S₈/G nanocomposite.

Fig. 2 shows the FT-IR spectrum of pure Co₉S₈ and Co₉S₈/G nanocomposites. In the spectrum of Co₉S₈ nanoflakes, the peak at 1130 indicates the S–O bending vibration of sulfonated groups of cobalt sulfide.²⁷ The peak at 1632 cm⁻¹ could be due to the presence of PVP on the surface of cobalt sulfide and a small peak at 619.9 cm⁻¹ is related to the stretching vibration of Co atoms in the surface of Co₉S₈.²⁸ In the case of Co₉S₈/G nanocomposite, the peak at 1397 cm⁻¹ corresponds to the epoxide group of graphene.^29,30

Fig. 2 FTIR spectrum of Co₉S₈/G nanocomposites (a) pure Co₉S₈ (b) Co₉S₈/G-a (c) Co₉S₈/G-b (d) Co₉S₈/G-c (e) Co₉S₈/G-d (f) Co₉S₈/G-e.

To further know about the optical properties of Co₉S₈/G nanocomposites, DRS-UV was recorded as given in Fig. 3. There are two major transmittance peaks observed. The peak at 270 nm indicates that the electronic conjugation is restored within the graphene sheets upon NaBH₄ reduction^31,32 and the peak at 225 nm might be due to the vibrations of S molecules in Co₉S₈ nanoflakes. The optical band gap of the composite material was calculated using the below equation from UV spectrum:

(αhν)ⁿ = A(hν − E_g)

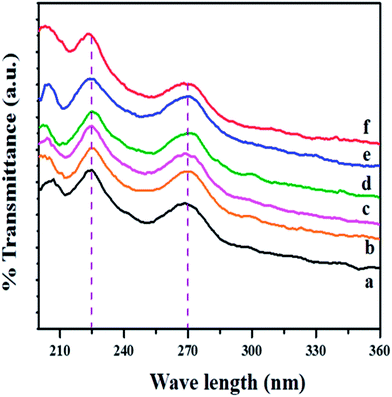Fig. 3 DRS UV spectrum of (a) pure Co₉S₈ (b) Co₉S₈/G-a (c) Co₉S₈/G-b (d) Co₉S₈/G-c (e) Co₉S₈/G-d (f) Co₉S₈/G-e.

To find the energy band gap, a plot between (αhν)² vs. (αν) was drawn, where ‘α’ is the absorption coefficient, ‘hν’ is the photon energy, ‘A’ is a constant, ‘E_g’ is the band gap, and ‘n’ is either 1/2 for an indirect transition or 2 for a direct transition. Thus, a plot of (αhν)² vs. (αν) is a straight line whose intercept on the energy axis gives the energy gap.

According to the above equation, based on the direct transition, a band gap of 3.2 eV was obtained for pure Co₉S₈, which matched well with the literature reports.³³ In the case of composites, the band gap value was decreased, which could be due to the fact that graphene sheets provide better electrical conductivity in the composite (Fig. 4).

Fig. 4 Optical band gap spectrum of pure Co₉S₈ and Co₉S₈/G composites.

Raman spectroscopy is widely used to study the crystalline structure of graphene and graphene composites. Fig. 5 shows the Raman spectra of pure graphene and Co₉S₈/G-d composite. For pure graphene, the two peaks at 1350 cm⁻¹ and 1580 cm⁻¹ can be assigned to the D and G band, respectively. The D-band is related to the vibrations of sp³ carbon atoms of disordered graphene, while the G band is a result of the first order scattering of E_2g mode of sp² carbon domains from graphene. The D/G ratio of the composite has increased than pristine graphite,³⁴ which confirmed the presence of graphene sheets.

Fig. 5 Raman spectrum of (a) graphene and (b) Co₉S₈/G composite.

Both the intensity and position of D and G bands lead to the structural changes in graphene matrix, which are affected by doping, layer number, defects etc.³⁵ The Co₉S₈/G-d composite showed a red shift of G band at 1576 cm⁻¹ compared with graphene, strongly suggesting the electronic interactions between graphene and Co₉S₈.³⁵ Also, a higher D/G intensity ratio (1.01) of Co₉S₈/G-d composite than pure graphene (0.90) is due to the decreased sp² carbon domains when Co₉S₈ are decorated between graphene sheets.³⁶

Thermogravimetric analysis was performed in air from room temperature to 1000 °C to quantify the amount of graphene, decomposition details and phase changes of the composite. Fig. 6 shows the TGA and DTA curves of pure Co₉S₈ and Co₉S₈/G nanocomposites. Initially, 8% weight loss of material was observed for pure graphene from 50° to 125 °C attributed to the evaporation of water and other organic molecules (Fig. S1†). A gradual weight loss was observed from the temperature 125° to 800 °C in graphene. The actual weight loss of the material could be observed after 800 °C due to burning of graphene and the weight of graphene after 1000 °C was 60%. There are three stages of weight loss observed for pure Co₉S₈ (Fig. 6a).

Fig. 6 Thermogravimetric TGA and DTA graph of (a) pure Co₉S₈ (b) Co₉S₈/G-a (c) Co₉S₈/G-b (d) Co₉S₈/G-c (e) Co₉S₈/G-d (f) Co₉S₈/G-e.

In DTA curve, the first two endothermic peaks at 87° and 400 °C might be due to the evaporation of solvent and PVP molecules in cobalt sulfide. The exothermic peak at 518 °C is attributed to oxidation and conversion of Co₉S₈ to Co₃O₄.³⁷ In Co₉S₈/G-d nanocomposite, the second exothermic peak is due to the burning of graphene and weight loss of graphene in this temperature is about 10% as observed in pure graphene. From Fig. 6e, the weight% of graphene in Co₉S₈/G-d nanocomposite was calculated to be around 12%. When the concentration of graphene was below 11 wt%, there was no second exothermic peak indicating that the weight loss of graphene was negligible in such composites.

The chemical composition of Co₉S₈/G-d nanocomposite was further investigated by using XPS analysis. An overall spectrum shows the presence of Co, S, C and O in the composites with no other element incorporated. In the deconvoluted spectra of C1s (Fig. 7b), a main peak was observed at 284.6 eV due to graphitic sp² carbon atoms. The other two peaks located at 286.2 and 287.6 are due to C–O and O–C–O, suggesting the presence of oxygen in graphene sheets.³⁸ The Co 2p spectrum was deconvoluted further, which gave major and minor peaks at 780.4 and 779.9 eV, corresponding to Co 2p_3/2 characteristic peak of cobalt sulfide. Another peak at 784.6 eV indicates the formation of octahedrally coordinated Co²⁺ ions in cobalt.³⁹ A trace amount of oxygen was also observed from XPS, which is due to the residual oxygen-containing groups (such as OH and COOH) bonded with C atoms in graphene. The peaks at 167.8 and 169.3 eV from S 2p spectrum is attributed to the sulphite and sulphates in cobalt sulfide. No peaks of sulfide are found in S 2p spectrum. This suggesting that the cobalt does not bind with sulfur atoms directly without involvement of oxygen in sulphite/sulphates.^40,41

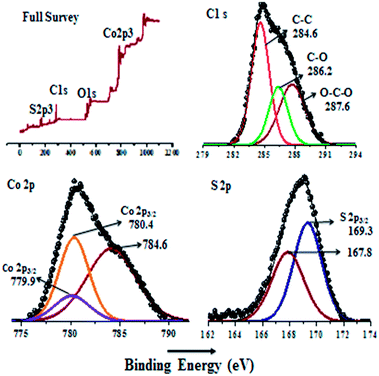Fig. 7 Wide scan XPS survey and core-level XPS spectrum of Co2p, C1s and S2p for Co₉S₈/G-d composite.

A homogeneous distribution of catalyst is essential for storage applications and in this regard, FESEM was recorded and the corresponding images of graphene, Co₉S₈ and Co₉S₈/G-d nanocomposites at various magnifications are shown in Fig. 8. Few layers of graphene with crumpled sheet like morphology could be seen in Fig. 8a₁ and a₂ indicates the graphene sheets were exfoliated during graphene synthesis⁴² and in the case of pure Co₉S₈, homogeneously shaped nanoflakes of Co₉S₈ with approximately 300 nm size could be seen (Fig. 8b₁ and b₂). Also could be seen from the images of Co₉S₈/G-d nanocomposite is that there is no sign of aggregation of Co₉S₈ nanoflakes and they are uniformly dispersed on the graphene sheets (Fig. 8c₁ and c₂). These individual nanoflakes can facilitate fast electron transfer between graphene and Co₉S₈ in electrochemical reactions rather than in their aggregation form. The corresponding EDS spectrum of Co₉S₈/G-d is given in Fig. 8c₃, which shows the presence of Co and S with 1 : 0.8 atomic wt% ratios. Fig. S2–S4† shows the mapping images of C in graphene, Co and S in Co₉S₈ and C, Co, S in Co₉S₈/G-d nanocomposite.

Fig. 8 FESEM and EDS spectrum of (a₁–a₃) graphene (b₁–b₃) pure Co₉S₈ (c₁–c₃) Co₉S₈/G-d nanocomposites.

The morphology of the samples was further analyzed by AFM technique. As given in Fig. 9a₁ and a₂, few layers of graphene sheets could be seen. The thickness of graphene is about 10 nm as observed from Fig. 9a₂ revealing the presence of few layer graphene sheets, which is in well agreement with SEM images. The typical thickness of individual graphene sheet is ∼0.34 nm.⁴³ Thus, the number of sheets in our study to be approximately 30 layers. The average size of Co₉S₈ was measured to be ∼500 nm from Fig. 9b₁ and b₂, which indicates the aggregation of Co₉S₈. In the case of Co₉S₈/G composite, a uniform size distribution of Co₉S₈ was observed, which is due to the prevention of agglomeration by graphene sheets.

Fig. 9 AFM images (a₁ and a₂) Graphene (b₁ and b₂) pure Co₉S₈ and (c₁ and c₂) Co₉S₈/G-d composite.

Electrochemical behavior and specific capacitance measurements

Performance of the prepared composite materials for supercapacitors was estimated by cyclic voltammetry (CV), galvanostatic charge–discharge and electrochemical impedance measurements in 6 M KOH aqueous solutions. The CV of a material assures the capacitive feature where in a large magnitude of current, rectangular shape of voltammograms and symmetricity in anodic and cathodic directions are features of an ideal capacitive behavior. The working cell potential range for the samples ranged between −0.1 to 0.3 V as obtained from CV measurements. Fig. 10 shows typical cyclic voltammograms of pure Co₉S₈ and composites at different scan rates. As evidenced from the figure, CV curves of all the electrode materials are symmetrical in nature, characteristic of ideal capacitive behavior⁴⁴ with quasi rectangular shape indicating the excellent capacitive behavior and a low contact resistance in the supercapacitor electrode.⁴⁵ No peaks were observed at different scan rates, suggesting that the electrode is charged and discharged at a pseudo-constant rate. As observed from the figure, cyclic voltammetry curves of all the composites are slightly different from pure Co₉S₈ as the overall specific capacitance for composites is enhanced due to the combined contributions from EDLC and pseudocapacitance of graphene, while the capacitance of Co₉S₈ is from pseudocapacitance only. The electric double layer capacitance of composites is influenced by the oxygen groups, which is present in the edges of graphene. These oxygen groups enhances the accessibility to hydrophilic surface in aqueous electrolytes.⁴⁶ The pseudocapacitance is due to the interactions between oxygen functional groups in graphene sheets and metal ions in electrolyte.⁴⁷ Also, the electrochemical capacitive behavior depends on the rate of charge transfer, i.e. the diffusion of anions and cations towards the electrode–electrolyte interfaces.

Fig. 10 Cyclic voltammetric behavior of (a) pure Co₉S₈ (b) Co₉S₈/G-a (c) Co₉S₈/G-b (d) Co₉S₈/G-c (e)Co₉S₈/G-d (f)Co₉S₈/G-e (g) Co₉S₈/G-x (h) Co₉S₈/G-z (j) cyclic voltammetry response of pure Co₉S₈ and Co₉S₈/G-d composite at 5 mV scan rate.

It could be seen that both the cathodic and anodic current response of pure Co₉S₈ is almost above the zero current level, suggesting poor electrochemical performance of the synthesized Co₉S₈ nanoflakes. The addition of graphene into Co₉S₈ can improve the dispersion of Co₉S₈ on the surface of graphene and provide more paths for ion diffusion due to the increased interface area between electrode and electrolyte. Like oxygen, sulfur ions in Co₉S₈ also provide pseudocapacitance activity due to the fact that sulfur and oxygen belong to the same group.¹⁶ CV measurements were conducted at various scan rates. The relative increment in current response with the scan rate constitutes an ideal capacitive behavior.⁴⁸ The specific capacitance was calculated from the CV curves according to the following formula^49,21

where, I₊ is the maximum current in the positive scan (amp), I₋ is the maximum current in the negative scan (amp), ‘m’ the mass of the active material coated on working electrode (g) and ‘ν’ is the scan rate (V s⁻¹).

To know the effect of graphene, CV was run for pure Co₉S₈ and the same has been compared with Co₉S₈/G-d composite (Fig. 10j). As clearly seen, the sample with graphene has a well-defined cyclic voltammetric behavior. Plot of scan rate verse specific capacitance of all samples shown in Fig. 11. From this plot, a maximum specific capacitance of 361.1, 460.8, 734.9, 808 and 788.2 F g⁻¹ was obtained for Co₉S₈/G-a, Co₉S₈/G-b, Co₉S₈/G-c, Co₉S₈/G-d and Co₉S₈/G-e composite electrodes respectively, at 5 mV s⁻¹ scan rate. At the same scan rate, pure Co₉S₈ electrode exhibited a specific capacitance of 350 F g⁻¹, which is lower than that of all other composite electrode materials. It is believed that such a large capacitance difference is caused by the introduction of graphene into Co₉S₈, which is the reason for obtaining high specific capacitances. The specific capacitance values decreased as the scan rate increased. At low scan rate, positive ions (K⁺) can easily diffuse into almost all available spaces of materials leading to sufficient insertion reaction. On the other hand, at higher scan rate, positive ions can approach only outer surface of the electrode and the material embedded in the inner space has little contribution to the capacitance behavior thus leading to a slight deviation from ideality and less capacitance.⁴⁴ On the basics of the CV results, it is well evidenced that the loading of graphene sheets in Co₉S₈ can provide better electrical conductivity in the network. Among the various composites, 9 wt% of graphene loaded (Co₉S₈/G-d) showed the highest capacitance. Thus, Co₉S₈/G-d composite provided large and better electrochemical activities towards the energy storage devices.

Fig. 11 Plot of scan rate versus specific capacitance graph.

To further know the effect of cobalt sulfide on graphene, CV measurements were done at various loadings of Co₉S₈. The composite was synthesized at three different concentrations of Co source with details given in the experimental section. Investigations showed that a maximum specific capacitance of 820 F g⁻¹ and 670 F g⁻¹ for Co₉S₈/G-x and Co₉S₈/G-z composite respectively. Thus, a high concentration (0.05 M) of cobalt sulfide in graphene leads to poor electrochemical performance.

Note that, the specific capacitance of Co₉S₈/G-x electrode has slightly higher specific capacitance than Co₉S₈/G-y electrode material at 5 mV s⁻¹ scan rate, but the values of specific capacitance decreased for higher scan rates due to the diffusion effect of ions. These results suggested the difficult movement of ions into electrode from electrolyte. Thus, it can be concluded that Co₉S₈/G-y electrode (viz. the composite prepared from 0.04 M Co precursor and 9 wt% graphene loading) showed the highest activity among the other composites. This increased specific capacitance of Co₉S₈/G-d or Co₉S₈/G-y electrode is due to the higher electrical conductivity than pure Co₉S₈.⁵⁰ This fact is supported by the electrical conductivity analysis given in Fig. 12. As seen from the figure, the presence of graphene increased the electrical conductivity of the composite, which further aided the increase in capacitance value.

Fig. 12 Electrical conductivity of (a) Co₉S₈/G-d composite and (b) pure Co₉S₈ at different temperatures.

The capacitance retention property of pure Co₉S₈ and Co₉S₈/G-d electrodes were investigated by repeating the CV measurements at 100 mV s⁻¹ scan rate for 2000 cycles. As shown in Fig. 13, the capacitance retention of Co₉S₈/G-d composite electrode was around 92.9% even after 2000 cycles, whereas pure Co₉S₈ exhibited retention of 89.9%, indicating high electrochemical cyclic stability of composite electrode.

Fig. 13 Capacitance retention of pure Co₉S₈ and Co₉S₈/G-d electrodes as function of cycle number measured at 100 mV s⁻¹ scan rate.

A comparison is made with the current material and the reported as given in Table 1 and as seen from the table, it can be seen that Co₉S₈/G reported in this paper has good activity and could be used for supercapacitor applications.

Table 1 Comparison of specific capacitance of various electrode materials towards the supercapacitor applications

Material	E^a	SR^b	SC^c	R^d
a Electrolyte.b Scan rate (mV s^−1).c Specific capacitance (F g^−1).d Reference.
Graphene/Mn3O4	6 M KOH	5	159	51
F-rGO-Ni(OH)2	1 M KCl	5	750	52
NiO/CNT	6 M KOH	—	523	53
MnO2/PPY/carbon nanofibre	2 M KCl	2	705	54
Graphitic petals/MnO2	1 M Na2SO4	2	580	55
Graphene/PANI	3 M KOH	1	463	56
Graphene/Sn	2 M KNO3	1	320	57
MWCNT/Co3O4	1 M Na2SO4	—	720.2	58
CoS	3 M KOH	—	508	23
CoS2-graphene	6 M KOH	5	253	59
Co9S8	6 M KOH	5	350	This work
Co9S8/G-d	6 M KOH	5	808	This work

---

To further assess the potential of Co₉S₈/G-d nanocomposite and Co₉S₈ electrodes, galvanostatic charge–discharge measurements were carried out. The charge–discharge test is a reliable method for the evaluation of electrochemical performances of electrode material under constant current condition. Fig. 14 shows the galvanostatic charge–discharge curve of pure Co₉S₈ and Co₉S₈/G-d composite. The charge–discharge experiment was carried out at a current density of 0.5 A g⁻¹ in the potential range −0.1 to 0.3 V. As can be observed, during the charging–discharging process, the charge curve is almost symmetric to its corresponding discharge counterpart with a slight curvature. The well symmetric and triangular nature of charge–discharge curve reveal the electric double layer capacitive and ideal capacitive behavior of the material.^60,61 Apart from double layer capacitance, pseudocapacitance behavior was also noted in charge–discharge curve suggesting that the overall capacitance of composite electrodes was a mixture of electric double layer and pseudocapacitors. Typically, three regions could be seen in the discharge curve. A sudden drop of the current at the starting point of discharge current (region I), due to the electrode–electrolyte interface resistance or internal resistance.⁶² The IR drop is attributed to the internal resistance of the electrode associated with the electrical connection resistance, bulk solution resistance and resistance of ion migration in electrode materials. The IR drop of pure Co₉S₈ electrode was much higher than that of Co₉S₈/G-d electrodes which is clearly seen in Fig. 14, indicating that the internal resistance of Co₉S₈ is much higher than the composite electrodes. This small internal resistance (IR) drop, indicate the presence of pseudocapacitance behavior along with the double layer capacitance.⁶³ The double layer capacitance behavior is due to the charge separation of electrode and electrolyte interfaces as seen in region II (a linear variation of the time dependence of the potential). The slope variation of time dependence of potential (region III) indicates the pseudocapacitance behavior that might be due to electrochemical adsorption–desorption or redox reaction at electrode–electrolyte interfaces.^64–66 A discharge time of 3.8 s was noticed for pure Co₉S₈ electrode, which is too low as compared to the composite electrode.

Fig. 14 Galvanostatic charge–discharge behavior of pure Co₉S₈ and Co₉S₈/G-d composite at current density 0.5 A g⁻¹.

Coulombic efficiency is an important factor which describes the stability of electrode materials through charge–discharge process. The coulombic efficiency of electrode is calculated according to the formula,⁶⁷

where, t_d is discharge duration and t_c is charging duration. As seen in Fig. 15, the initial coulombic efficiency of both electrodes is low, which is due to the re-stacking of graphene layers in Co₉S₈/G-d composite and side reactions between graphene sheets and electrolyte arising from abundant functional groups such as COOH and OH, etc. in graphene during charging of electrode.⁶⁸ Also, the coulombic efficiency of electrodes were gradually increased from the 1^st cycle to 1000^th cycle, which could be attributed due to the activation effect of electrodes during long term charging–discharging process.⁶⁹ Notably, the Co₉S₈/G-d composite electrode shows the coulombic efficiency of ∼99.2% even after 1000 cycles, which is higher than that of bare Co₉S₈ (86.7%). This result suggested that the energy loss of Co₉S₈/G-d electrode during discharge process was low. Fig. S5 & S6† shows the galvanostatic charge–discharge of Co₉S₈/G-d composite and pure Co₉S₈ at different current densities. It can be seen that the IR drop is negligible at low discharge current density as both inner and outer pore surfaces of electrode could be utilized for electrolyte propagation during the charge–discharge process. Thus, the electrode has stored a high charge at low discharge current density.⁷⁰

Fig. 15 Coulombic efficiency of Co₉S₈ and Co₉S₈/G-d electrodes at current density of 0.5 A g⁻¹.

EIS analysis was used to investigate the fundamental behavior of the electrode materials for supercapacitors like charge transport phenomenon at the electrode–electrolyte interface. Electrochemical Impedance Spectroscopy (EIS) were measured with an AC perturbation of 0.01 V in the frequency range of 0.01 Hz to 10⁵ Hz at an open circuit potential. Fig. 16 shows the Nyquist plots of Co₉S₈ and composite electrodes with their corresponding equivalent circuit. All spectra shows a semicircle in the high frequency region (inset pictures), a straight line inclined at a constant phase in the mid frequency region and an almost vertical capacitive line in the low frequency region. The impedance plot of Co₉S₈ was increased sharply at low frequency and tends to become vertical due to non-faradic charge storage mechanism. This vertical straight 45° line shows the pure capacitive behavior of cobalt sulfide.⁷¹ The intersection of curve at real axis in high frequency region gives the solution resistance (R_s) which reflects the ionic conductivity of electrolyte system and the diameter of the semi-circle represents interfacial charge transfer resistance (R_ct), which is due to the electron conductivity of electrode material.⁶⁷ It is well known that a large semicircle indicates high interfacial charge transfer resistance, which is due to the poor conductivity of the electrode. All the parameters extracted from EIS spectrum are given in Table 2 and as seen, both solution and charge transfer resistance of Co₉S₈/G-d or Co₉S₈/G-y composite electrode were less than pure Co₉S₈, which could be attributed to the enhanced conductivity of graphene sheets.⁷²

Fig. 16 Nyquist plots of (a) pure Co₉S₈ and (b) Co₉S₈/G-d composite.

Table 2 Comparison of observed results of Co₉S₈/G-d and Co₉S₈ electrodes from EIS analysis

Sample	Rs (Ω)	Rct (Ω)	τ (s)	fknee (Hz)
Co9S8	4.1	26.3	5 × 10^−2	9.766 × 10^−2
Co9S8/G-d or Co9S8/G-y	3.5	19	1.64 × 10^−5	4.542 × 10^−1

---

The time constant of electrode materials can be calculated from the frequency (f*) corresponding to the maximum imaginary component (−Im Z′′) of the semicircle by using expression⁵⁹

Low time constant is an important characteristic for fast charge-discharge functioning of the supercapacitor electrodes. The time constant of Co₉S₈/G-d was calculated to be 1.96 × 10⁻⁵ seconds, which is lower than that of pure Co₉S₈ electrode suggesting the fast charge–discharge characteristic behavior of composite due to the presence of graphene.

Bode plots of phase angle and bode plots of total impedance verses frequency are shown in Fig. 17. The phase angle of both electrodes were observed to be close to −60° in low frequency, which indicates the capacitor behavior of electrodes. The amplitude of the total impedance versus frequency plots show three slopes at different frequency regions. The slope of both electrodes showed large value at low frequency region (1–0.01 Hz), which is probably due to the resistive components of the interfaces. The present study emphasizes the combination of both resistive and capacitive behavior at high frequency region (10⁵–100 Hz) and only capacitive behavior at mid frequency region (100–1 Hz). Compared with pure Co₉S₈, the slope value of Co₉S_8/G-d electrode at both mid and high frequencies region was small, which evidences for more capacitive behavior of composite than Co₉S₈ electrode.

Fig. 17 Bode plots of phase angle and bode plots of total impedance verses frequency of (a) Co₉S₈/G-d composite and (b) pure Co₉S₈.

“Knee frequency (f_knee)” is another important characteristic of energy storage devices. It refers to the transition point between the high frequency and low frequency component, which is a measure of the power capability of capacitors. The electrochemical capacitor can be charged more rapidly and high power could be achieved with higher knee frequency.⁷³ A high knee frequency of 4.542 × 10⁻⁵ Hz have been obtained for Co₉S₈/G-d electrode, which indicated that the developed composite is a promising electrode material for supercapacitor applications.

Conclusions

In summary, a rapid, low cost route for the synthesis of the Co₉S₈ nanoflakes/graphene composites have been developed and a systematic investigation was carried out on the effects of graphene loading on supercapacitor performance of the composite materials. The composite electrode showed enhanced specific capacitance than pure Co₉S₈, which is due to contribution of high electrical conductivity and pseudocapacitance of graphene and Co₉S₈. A maximum specific capacitance of 808 F g⁻¹ was obtained for Co₉S₈/G composites with 9 wt% graphene loading. The galvanostatic charge–discharge measurement shows the excellent cyclic stability of both electrodes. The EIS measurement showed that the prepared electrode materials has low impedance and hence such hybrid Co₉S₈/G composite electrodes are promising materials with potential applications in high performance supercapacitors.

Acknowledgements

This work was carried out with the help of VIT management through research scholarship. This work was also conducted under the framework of Research and Development Program of the Korea Institute of Energy Research (KIER) (B3-2467-07).

References

1. L. L. Zhang, R. Zhou and X. S. Zhao, J. Mater. Chem., 2010, 20, 5983–5992.
2. Z. Gao, W. Yang, J. Wang, H. Yan, Y. Yao, J. Ma, B. Wang, M. Zhang and L. Liu, Electrochim. Acta, 2013, 91, 185–194.
3. Z. Lei, F. Shi and L. Lu, ACS Appl. Mater. Interfaces, 2012, 4, 1058–1064.
4. M. Zhi, C. Xiang, J. Li, M. Li and N. Wu, Nanoscale, 2013, 5, 72–88.
5. M. Liu, W. W. Tjiu, J. Pan, C. Zhang, W. Gao and T. Liu, Nanoscale, 2014, 6, 4233–4242.
6. X. C. Dong, H. Xu, X. W. Wang, Y. X. Huang, M. B. ChanPark, H. Zhang, L. H. Wang, W. Huang and P. Chen, ACS Nano, 2012, 6, 3206–3213.
7. Y. G. Zhu, G. S. Cao, C. Y. Sun, J. Xie, S. Y. Liu, T. J. Zhu, X. B. Zhao and H. Y. Yang, RSC Adv., 2013, 3, 19409–19415.
8. Y. Liu, Y. Ying, Y. Mao, L. Gu, Y. Wang and X. Peng, Nanoscale, 2013, 5, 9134–9140.
9. T. Lu, Y. Zhang, H. Li, L. Pan, Y. Li and Z. Sun, Electrochim. Acta, 2010, 55, 4170–4173.
10. S. D. Perera, A. D. Liyanage, N. Nijem, J. P. Ferraris, Y. J. Chabal and K. J. Balkus Jr, J. Power Sources, 2013, 230, 130–137.
11. P. A. Basnayaka, M. K. Ram, E. K. Stefanakos and A. Kumar, Electrochim. Acta, 2013, 92, 376–382.
12. H. H. Chang, C. K. Chang, Y. C. Tsai and C. S. Liao, Carbon, 2012, 50, 2331–2336.
13. J. L. H. Xie, Y. Li, J. Liu and Z. Li, J. Power Sources, 2011, 196, 10775–10781.
14. M. Jayalakshmi and M. M. Rao, J. Power Sources, 2006, 157, 624–629.
15. J. Wang, S. H. Ng, G. X. Wang, J. Chen, L. Zhao, Y. Chen and H. K. Liu, J. Power Sources, 2006, 159, 287–290.
16. F. Tao, Y. Q. Zhao, G. Q. Zhang and H. L. Li, Electrochem. Commun., 2007, 9, 1282–1287.
17. Y. X. Zhou, H. B. Yao, Y. Wang, H. L. Liu, M. R. Gao, P. K. Shen and S. H. Yu, Chem.–Eur. J., 2010, 16, 12000–12007.
18. N. Mahmood, C. Zhang, J. Jiang, F. Liu and Y. Hou, Chem.–Eur. J., 2013, 19, 5183–5190.
19. B. Qu, Y. Chen, M. Zhang, L. Hu, D. Lei, B. Lu, Q. Li, Y. Wang, L. Chen and T. Wang, Nanoscale, 2012, 4, 7810–7816.
20. A. N. Grace, R. Ramachandran, M. Vinoba, S. Y. Choi, D. H. Chu, Y. Yoon, S. C. Nam and S. K. Jeong, Electroanalysis, 2014, 26(1), 199–208.
21. R. Ramachandran, S. Felix, G. M. Joshi, B. P. C. Raghupathy, S. K. Jeong and A. N. Grace, Mater. Res. Bull., 2013, 48, 3834–3842.
22. C. Y. Chen, Z. Y. Shih, Z. Yang and H. T. Chang, J. Power Sources, 2012, 215, 43–47.
23. Z. Yang, C. Y. Chen and H. T. Chang, J. Power Sources, 2011, 196, 7874–7877.
24. Y. Zhao, J. Li, C. Wu and L. Guan, Nanoscale Res. Lett., 2011, 6, 71–76.
25. Q. H. Wang, L. F. Jiao, Y. Han, H. M. Du, W. X. Peng, Q. N. Huan, D. W. Song, Y. C. Si, Y. J. Wang and H. T. Yuan, J. Phys. Chem., 2011, 115, 8300–8304.
26. H. Hu, Y. Liu, Q. Wang, J. Zhao and Y. Liang, Mater. Lett., 2011, 65, 2582–2584.
27. T. V. Sathisha, B. E. Kumaraswamy, S. Reddya, B. N. Chandrashekar and B. Eswarappa, J. Mol. Liq., 2012, 172, 53–58.
28. W. Dong, X. Wang, B. Li, L. Wang, B. Chen, C. Li, X. Li and T. Z. Zhanshi, Dalton Trans., 2011, 40, 243–248.
29. M. Zhou, Y. Wang, Y. Zhai, W. Ren, F. Wang and S. Dong, Chem.–Eur. J., 2009, 15, 6116–6120.
30. P. G. Ren, D. X. Yang, X. Ji, T. Chen and Z. M. Li, Nanotechnology, 2011, 22, 055705–055712.
31. D. Li, M. B. Muller, S. Gilje, R. B. Kaner and G. G. Wallace, Nat. Nanotechnol., 2008, 3, 101–105.
32. G. Wang, L. T. Jia, Y. Zhu, B. Hou, D. B. Li and Y. H. Sun, RSC Adv., 2012, 12, 11249–11252.
33. F. Srouji, M. Afzaal, J. Waters and P. O'Brien, Chem. Vap. Deposition, 2005, 11, 91.
34. G. X. Wang, J. Yang, J. Park, X. L. Gou, B. Wang and H. Liu, J. Phys. Chem. C, 2008, 112, 8192–8195.
35. C. Fu, G. Zhao, H. Zhang and S. Li, Int. J. Electrochem. Sci., 2014, 9, 46–60.
36. S. Stankovich, D. A. Dikin, R. D. Piner, K. A. Kohlhaas, A. Kleinhammes, Y. Jia, Y. Wu, S. T. Nguyen and R. S. Ruoff, Carbon, 2007, 45, 1558–1565.
37. G. Huang, T. Chen, Z. Wang, K. Chang and W. Chen, J. Power Sources, 2013, 235, 122–128.
38. J. Zhang, J. Jiang, H. Li and X. S. Zhao, Energy Environ. Sci., 2011, 4, 4009–4015.
39. T. Fix, M. Liberati, H. Aubriet, S. L. Sahonta, R. Bali, C. Becker, D. Ruch, J. L. MacManus-Driscoll, E. Arenholz and M. G. Blamire, New J. Phys., 2009, 11, 073042–073051.
40. L. Liu, J. Power Sources, 2013, 239, 24–29.
41. S. Makhseed, F. Al-Kharafi, J. Samuel and B. Ateya, Catal. Commun., 2009, 10, 1284–1287.
42. S. Y. Yang, K. H. Chang, Y. L. Huang, Y. F. Lee, H. W. Tien, S. M. Li, Y. H. Lee, C. H. Liu, C. C. Ma and C. C. Hu, Electrochem. Commun., 2012, 14, 39–42.
43. Z. H. Sheng, L. Shao, J. J. Chen, W. J. Bao, F. B. Wang and X. H. Xia, ACS Nano, 2011, 5(6), 4350–4358.
44. J. Zhu and J. He, ACS Appl. Mater. Interfaces, 2012, 4, 1770–1776.
45. Y. Li, N. Zhao, C. Shi, E. Liu and C. He, J. Phys. Chem. C, 2012, 116, 25226–25232.
46. M. V. Kuyilazhagan, M. V. Vaishampayam and M. V. Shelke, J. Mater. Chem. A, 2014, 2, 2152–2159.
47. C. T. Hsieh, W. Y. Chen and Y. S. Cheng, Electrochim. Acta, 2010, 55, 5294–5300.
48. D. P. Dubal, D. S. Dhawale, R. R. Salunkhe and C. D. Lokhande, J. Electroanal. Chem., 2010, 647, 60–65.
49. C. Bora and S. K. Dolui, Polymer, 2012, 53, 923–932.
50. S. H. Tamboli, B. S. kim, G. Choi, H. Lee, D. Lee, U. M. Patil, J. Lim, S. B. Kulkarani, S. C. Jun and H. H. Cho, J. Mater. Chem. A, 2014, 2, 5077–5086.
51. B. Wang, J. Park, C. Wang, H. Ahn and G. Wang, Electrochim. Acta, 2010, 55, 6812–6817.
52. Z. Sun and X. Lu, Ind. Eng. Chem. Res., 2012, 51, 9973–9979.
53. C. Z. Gao, L. H. Yuan, S. L. Chen and X. G. Zhang, J. Solid State Electrochem., 2009, 13, 1251–1257.
54. J. G. Wang, Y. Yang, Z. H. Huang and F. Kang, J. Mater. Chem., 2012, 22, 16943–16949.
55. G. Xiong, K. P. S. S. Hembram, R. G. Reifenberger and T. S. Fisher, J. Power Sources, 2013, 227, 254–259.
56. H. Liu, Y. Wang, X. Gou, T. Qi, J. Yang and Y. Ding, Mater. Sci. Eng., B, 2013, 178, 293–298.
57. Z. Qin, Z. J. Li, M. Zhang, B. C. Yang and R. A. Outlaw, J. Power Sources, 2012, 217, 303–308.
58. A. S. Adekunle, K. I. Ozoemena and B. O. Agboola, J. Solid State Electrochem., 2013, 17, 1311–1320.
59. B. Wang, J. Park, D. Su, C. Wang, H. Ahn and G. Wang, J. Mater. Chem., 2012, 22, 15750–15756.
60. G. S. Gund, D. P. Dubalb, B. H. Patil, S. S. Shinde and C. D. Lokhande, Electrochim. Acta, 2013, 92, 205–215.
61. J. Yan, J. Liu, Z. Fan, T. Wei and L. Zhang, Carbon, 2012, 50, 2179–2188.
62. A. Pendashteh, M. F. Mousavi and M. S. Rahmanifar, Electrochim. Acta, 2013, 88, 347–357.
63. L. Li, K. H. Seng, Z. Chen, H. Liu, I. P. Nevirkovets and Z. Guo, Electrochim. Acta, 2013, 87, 801–808.
64. B. G. Choi, M. Yang, W. H. Hong, J. W. Choi and Y. S. Huh, ACS Nano, 2012, 6, 4020–4028.
65. D. P. Dubal, V. J. Fulari and C. D. Lokhande, Microporous Mesoporous Mater., 2012, 151, 511–516.
66. W. Sugimoto, H. Iwata, Y. Yasunaga, Y. Murakami and Y. Takasu, Angew. Chem., Int. Ed., 2003, 42, 4092–4096.
67. Q. Wang, L. Jiao, H. Du, Y. Si, Y. Wang and H. Yuan, J. Mater. Chem., 2012, 22, 21387–21391.
68. Z. S. Wu, G. Zhou, L. C. Yin, W. Ren, F. Li and H. M. Cheng, Nano Energy, 2012, 1, 107–131.
69. J. Xie, X. Sun, N. Zhang, K. Xu, M. Zhou and Y. Xie, Nano Energy, 2013, 2, 65–74.
70. J. Xu, X. Gu, J. Cao, W. Wang and Z. Chen, J. Solid State Electrochem., 2012, 16(8), 2667–2674.
71. Y. Wang, Z. Shi, Y. Q. Huang, Y. F. Ma, C. Y. Wang, M. M. Chen and Y. Y. Chen, J. Phys. Chem. C, 2009, 113, 13103–13107.
72. H. Su, T. Wang, S. Zhang, J. Song, C. Mao, H. Niu, B. Jin, J. Wu and Y. Tian, Solid State Sci., 2012, 14, 677–681.
73. R. Ding, L. Qi, M. Jia and H. Wang, J. Appl. Electrochem., 2012, 42, 1033–1043.

---

Footnote

† Electronic supplementary information (ESI) available: Further details of graphene TGA graph, SEM mapping images and galvanostatic charge–discharge behaviour of composite and pure Co₉S₈. See DOI: 10.1039/c4ra01515k

---