Charge transport modeling in bisphenazine derivative dimers as discotic liquid crystals: a TDDFT study

Abstract

A theoretical study was conducted on bisphenazine derivatives which behave as discotic liquid crystals (DLCs). Different cofacial dimeric conformations were studied in order to model the packing in a column, which is the main arrangement found in a DLC. The intermolecular charge transport process was assessed employing the charge transfer integral “J” in the context of Marcus theory. This parameter was obtained via the TD-Split method with the M06L functional and a basis set containing diffuse and polarization functions. The resulting systems display a charge displacement from one molecule to the other. Furthermore, a bonding interaction is observed in the frontier molecular orbitals; this suggests that the best geometries for effective electron transfer are those in which the molecules are rotated, and not eclipsed or widely displaced geometries. Additionally, computations of the monomer were performed to study the electronic structure and the electronic excitations. This methodology provided new insights into one-dimensional migration of charges in DLC compounds by employing TDDFT.

---

1. Introduction

Supramolecular interactions are common in nature, and most of these are non-covalent interactions such as hydrogen bonding, π-stacking, polar–nonpolar and charge transfer. These forces can build functional materials by self-organization, structures such as polypeptides or the double helix of nucleic acids, and can produce biological functions that are vital for life, such as the bonding of oxygen to hemoglobin, or DNA replication.¹

Nowadays, these phenomena are vital to design a wide range of devices like solar cells, nanoelectronics and molecular electronics which have a wide variety of applications.² Research into supramolecular materials produces large-scale structures, which is of high interest. One of the most intriguing types of self-organizing materials are liquid crystals (LCs),³ also called mesogens. These materials combine the fluidity of liquids and the anisotropy of crystals, and they are defined as “orientationally ordered” liquids or “positionally disordered” crystals because they show an intermediate phase (mesophase) in which their structure is both oriented and fluid, and displays attractive color changes.¹ These factors generate interesting electronic and structural properties, like the discovery made by Haarer et al. in 1993 of the electronic conduction in a LC phase of hexapentyloxytriphenylene (HPT); this currently still attracts great attention and has lead to technological advancement.⁴

The essential design of a LC molecule is a structure consisting of a central core (often aromatic) and long, flexible peripheral substituents (chains). There are several classes of LCs based on their structure, such as calamitic or rod-like mesogens, bent or banana molecular shape and discotic liquid crystals (DLCs).¹ DLCs are mesophases constituted by rigid planar aromatic cores covalently bound to several long alkyl chains, and each molecule forms a disk shape. They are able to self-align in a controlled manner over long distances, and thus forming quasi one-dimensional (1D) semiconductors. This self alignment is due to interactions between adjacent molecules which results in overlapping of the aromatic cores, and this structure is refer to as columnar (Col) or nematic (N) mesogens. The long lateral alkyl chains provide fluidity to the system, which is responsible for the liquid crystalline properties. Fig. 1 illustrates a model of columnar packing for a general DLC.⁵

Fig. 1 Scheme of alignment observed in DLCs.

It has been shown that charges and excitons travel faster through the molecules than between the columns, which is a key property for several electronic devices like organic field-effect transistors, organic light-emitting diodes and organic photovoltaic cells. These systems are the foundation of commercial products like flat screen television, wristwatches, laptop screens, digital clocks, thermometers and p/n-type photovoltaic cells. The operation of these devices relies on the efficient charge transport through the columnar structures of a DLC, when placed between electrodes.⁶

On a molecular scale, the interactions between the central aromatic cores are weak, and are predominantly van der Waals (vdW) forces. There are several strategies to take into account these weak interactions in density functional theory (DFT) calculations, which are models that have been proposed for non-covalent systems.⁷ Due to the computational advantages of local functionals that include long range corrections, such as M06L,⁸ it is possible to carry out both the simulations of moderate and large-sized systems, and the study of non-covalent interactions.⁹ Also, it has been shown that for this class of calculations, basis set with diffuse and polarization functions offers an affordable way to study charge transfer processes.¹⁰

Charge transfer is one of the most important phenomena in LCs. This process can be studied using any theoretical approach within the Marcus theory framework, such as DFT methods which are the most popular due to high accuracy and affordable computational cost.¹¹

Charge transport in DLC mesogens is mostly described as the movement of electrons (or holes) from a disk to another adjacent disk along the axis of the π-stacking. In an energy-gap-based model expressed by Brédas et. al.,^11a which characterizes the parameters that govern the charge transport in discotic mesophases, the transfer integral “J” is assessed for either holes (or electrons) by half the energy difference between the HOMO (LUMO) energy of the monomer with the HOMO (LUMO) energy of the neutral dimer. This approach shows some limitations as it does not take into account the re-arrangement of the electronic density during the charge transfer, or the perturbation of the electronic structure of the system in response to the transported electron in a LC. Neuhauser and co-workers¹² studied the charge transfer from a donor to an acceptor using a “dynamic” method called time-dependent split (TD-Split). They showed that the neutral static picture underestimates the charge transfer rate but the tendency of the energy remains the same when the intermolecular distance changes.

In TD-Split, the transfer integral “J” is calculated using the HOMO → LUMO vertical excitation energy of a negatively (−1) charged dimeric system. Here, the ground state has an extra shared electron between the fragments which corresponds to the halfway point of the transfer process. This excitation energy is computed employing a time dependent method.^12a,13 Thus, the resulting transfer integrals in TD-Split are associated with the rate of electron transfer of the system. As well, TD-Split takes into account the movement of the electron through the column on a reduced dimeric system, and these considerations are neglected in static calculations. Although static splitting does offers a good approximation to the electronic transfer at short distances, the use of a dynamic approach becomes more important as the separation between monomers increases.^12a

Many different LC mesogens have been reported with a variety of cores including benzene, naphthalene, phenanthrene, anthraquinone, triphenylene, perylene, hexabenzocoronene, pyrene, macrocyclic cores like porphyrins or phthalocyanine, triazine, hexaazatriphenylene and phenazines, and all of which have long peripheral alkyl chains.^1,14 The report on the synthesis and characterization of planar, liquid crystalline phenazine and bisphenazines compounds with the following peripheral chains: n-C₁₀H₂₁, n-C₁₁H₂₃, n-C₁₄H₂₉, n-C₁₆H₃₃, 2-methylhexyl, and 3,7-dimethyloctyl, shows effective π–π stacking structures, charge mobility and liquid crystal properties.¹⁵ Further studies have looked at substituting the phenazine chromophore with a crown,¹⁶ as well as structural effects from the electron transfer properties in tetrabenzophenazine, dibenzodipyridophenazine and tetrapyridophenazine,¹⁷ and lastly phenazine-based systems as anion sensors.¹⁸

This paper aims to provide more insight on the charge transfer process of the bisphenazines dimer structures reported by Harris et al.^15b via the TD-Split study of the intermolecular charge transfer in the face-to-face or cofacial packing of these structures. Since it is the aromatic core which is predominantely responsible for the charge mobility along the columnar structure or a DLC, the alkyl chains were reduced to methyl groups for this study (Fig. 2).

Fig. 2 Bisphenazine derivative general structure.

To properly assess the fluctuation of the geometries in the LC phase, we considered different conformations of one molecule respect to the other in a dimeric system. Three different geometrical movements were studied (Fig. 3): the variation of intermolecular distances (Fig. 3a), rotation of one molecule around the stacking axis with a fixed intermolecular separation (Fig. 3b), and lastly the movement of one molecule with respect to the other molecule along the axis contained in the plane where the molecules lie (Fig. 3c).

Fig. 3 General scheme of the proposed geometrical changes for the stacked dimers. (a) Separation of the molecules, (b) rotation of one molecule respect to the other and (c) translation of one molecule respect to the other.

2. Computational details

Density functional theory (DFT) as implemented in Gaussian 09 software¹⁹ was employed to perform the computations of the bisphenazine monomer and dimers systems.

The M06L functional⁸ and the Gaussian basis set along with a set of diffuse s-functions and a set of d and p polarization functions added to the atoms, 6-31+G(d,p),²⁰ was employed. These theoretical level were chosen based on the fact that they are efficient for computations of properties of non-covalent systems. The optimized monomer structure was proven to be one of the energy minima by calculating vibrational frequencies. The absorption wavelengths and oscillator strengths were computed by means of time-dependent density functional theory (TDDFT)²¹ and solvation effects were modeled by the Polarizable Continuum Model (PCM).²²

TD-Split dynamic approach proposed by Neuhauser¹² was applied to assess the charge transfer integral in the dimer conformations (cofacial or face-to-face), taking into account an extra electron shared between the molecules. This shared electron represents the halfway point of the electron transfer through a column with the respective dimeric geometries.

For DFT, the main challenge is the determination of the most appropriate initial and final states of the transfer integral “J” in the Marcus formalism:

J = |〈ψ_F|H|ψ_I〉|² (1)

where |ψ_I〉 and 〈ψ_F| are the initial and final states and H is the electronic coupling Hamiltonian.²³ The transfer integral J must be computed as accurately as possible, with proper choice of initial and final states for predictive calculations.

By using the vertical electronic excitation of the −1 charged dimer from its delocalized ground state, the initial and final states in the transfer integral J are well chosen due to the exclusion of non-physical re-arrangement of the electrons because of the localization of the extra electron. The time-dependent dynamic is thus directly associated with transport, since the added charge is delocalized. In this method, the initial state is the ground static density matrix for the entire (donor and acceptor) charged system. A time dependent excitation is applied and the response to this excitation is a measure of electron transfer rate. Thus this computational tool is effective for this study, and it is investigating an area of LCs which was not previously explored.

3. Results and discussion

3.1 Electronic structure and TDDFT study of the monomer

DFT studies on the electronic properties of bisphenzine related compounds have been previously reported in literature. Some of these include the electron density study of dehydrogenated pyrene systems, radicals and pyrene derivatives coordinated to cobalt employing the quantum theory of atoms in molecules (QTAIM) and the electron localization function (ELF).²⁴ The study of the optical properties of pyrene derivatives coordinated to palladium and platinum,²⁵ as well as the study of phenazine and bisphenazine derivatives substituted with NO₂, halogens, alkyl groups, amongst others.²⁶ In general, our results are in accordance with the previously reported data, especially since the energy of the frontier molecular orbitals and the HOMO–LUMO gap are very similar to the above mentioned reports for the analogous compounds.

A graphical representation of molecular orbitals (MOs) isosurfaces, the highest occupied MOs (HOMO, HOMO−1, HOMO−2 and HOMO−3) and the lowest unoccupied MOs (LUMO, LUMO+1, LUMO+2 and LUMO+3) are depicted in Fig. 4.

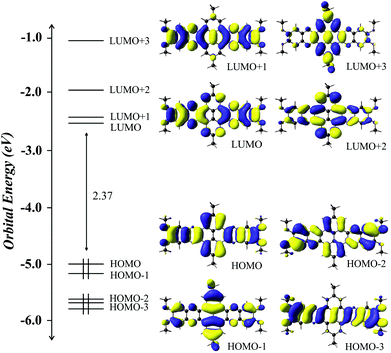Fig. 4 Calculated frontier MOs energy levels and isosurfaces plots of FMO involved in the calculated transitions.

These MOs show no large contribution from the peripheral substituents and are formed by the π orbitals which extend over the entire macrocycle, indicating an electronic delocalization.

The HOMO is localized over the macrocycle and shows a bonding character with some orbital contribution from the substituent groups, mainly from the oxygen atoms. On the other hand, the LUMO orbital, which is also extended over the macrocycle, shows an antibonding character.

The energy level diagram of the bisphenazine monomer presents a large HOMO–LUMO band gap of 2.37 eV but the HOMO and HOMO−1 as well as the LUMO and LUMO+1 are quasi degenerated orbitals.

The calculation of a UV-vis absorption spectrum by TDDFT provides detailed understanding of the origin and character of a molecule's electronic transitions.

The intensity of each band in the spectrum is proportional to the calculated oscillator strength (f), which is indicative of the probability that a transition to occur.

The computations of the excitation energies, oscillator strengths and compositions of the electronic transitions for the complex are reported in Table 1. The calculated absorption energies are compared with the experimental bands, see Table 1.²⁷

Table 1 Calculated wavelength (λ) in nm, energy (E) in eV, oscillator strength (f), active MOs and their contributions (in %) for the vertical excitations from TDDFT

λ (nm) abs. exp	λ (nm) abs. calc.	E (eV) calc.	f	Active MO		%
428	472	2.62	0.283	145 → 147	HOMO → LUMO+1	86.3
404	402	3.08	0.804	143 → 146	HOMO−2 → LUMO	80.9
318	317	3.91	0.030	138 → 147	HOMO−6 → LUMO+1	81.3
288	282	4.39	0.043	138 → 148	HOMO−6 → LUMO+2	45.4
				144 → 149	HOMO−1 → LUMO+3	46.6
244	243	5.10	0.361	139 → 149	HOMO−5 → LUMO+3	46.1
				142 → 151	HOMO−3 → LUMO+5	35.6

---

The TDDFT results agree with the reported experimental data. The experimental spectrum exhibits five main absorption bands located at 428, 404, 318, 288 and 244 nm. This agreement between the experimental and the theoretical results indicates the accuracy of the electronic structure of the optimized systems. The biggest discrepancy is observed for the signal located at 428 nm, which was calculated to be at 472 nm with TDDFT and corresponds to the transition of HOMO → LUMO+1, and is characterized as π–π*. Also, the transition at 402 nm has the highest oscillator strength and is mainly of the type HOMO−2 → LUMO.

Transitions at higher energy correspond to transitions between occupied orbitals of lower energy and unoccupied orbitals of higher energy, which involve orbitals lying along of the bisphenazine and orbitals localized mainly on the pyrene fragment.

3.2 TD-Split study for the dimeric systems

It is known that phenazines behave like discotic liquid crystals (DLCs) and display charge transport properties due mainly to the interactions that are between the π clouds of the molecules. Hence, LC behavior is exemplified by different stacked geometries of dimers. With this in mind, different cofacial dimers formed by bisphenazines were calculated in order to use them as models of the packing in a column. The long alkyl chains were reduced to methyl groups since the most important interaction is between the rings. The TD-Split method is used in the herein report to characterize the parameters that govern the charge transport in these discotic mesophases, in a molecular scale.

In general, the study of the idealized cofacial dimer structures represented by eclipsed conformations and a series of different conformations with the rotation and movement of one molecule with respect to another, was performed. In this sense, the calculation of the dimeric structures with the variation of the intermolecular distances between 3.0 Å and 5.0 Å were assessed. The rotational disorder was modeled through the movement when one molecule rotates around a stacking axis (keeping the intermolecular separation fixed, the energy was assessed every 20°). Finally, the third geometrical variation that needs to be considered is the displacement of one molecule with respect to another one along one axis. Those calculations were carried out considering a displacement of the molecules every 0.5 Å (see Fig. 3).

Due to a large degree of geometric fluctuations and absence of crystalline order, the charge transport in DLC phases is mainly described within a phonon-assisted hopping between the discotic mesogens. The phonon-assisted hopping between the discotic mesogens is based on the idea that electrons (or holes) are localized on the discs and they hop from one disc to the adjacent one along the axis of the π-stacking. In this way, this methodology provides new insights for the study of the one-dimensional migration of charge in phenazine compounds employing TDDFT.

Fig. 5a shows the evolution of the TDDFT vertical excitation energies (eV) as a function of the intermolecular separation of the bisphenazines between 3.0 Å and 5.0 Å. As observed, the energy decays exponentially as the intermolecular separation increases. This tendency might be explained by the decrease of the π-orbital overlap when the two macrocycles are getting apart, vide infra. The experimental equilibrium distance between the phenazines stacked face-to-face free metal molecules is ∼3.6 Å.²⁸ At this distance, the found splitting TDDFT energy is near to 4.0 eV.

Fig. 5 HOMO → LUMO TDDFT vertical excitation energies for the −1 charged dimer; M06-L/6-31+G(d,p) theoretical level was employed for all calculations. (a) Energy as a function of the intermolecular distance, (b) energy as a function of the rotation and (c) energy as a function of the translation.

On the other hand, the evolution of the TD-Split energies in the bisphenazine dimers at fixed distance of 3.6 Å and rotating one molecule with respect to the other around the stacking axis is presented in Fig. 5b. In order to carry out this study, the rotations from 0° to 180° by sequential steps of 20° were performed. The results indicate that the best conformations for charge transfer would be the systems with rotations of 0°, 20°, 160° and 180° where the maximum of the transfer integral are shown. Those values are followed by 40° and 140°. The mobility is slightly reduced for angles of 60° and 120° and dramatically reduced for angles 80° and 100°. All these rotated conformations, excluding 0° and 180°, show dipole moment vectors with a perpendicular direction to the plane that contains the molecules (Fig. 6). The dipole moment is calculated as the sum of the product r_iq_i that runs over all charged atoms of the system; the vector r_i is the position of the ith atom and q_i is the respective charge value.²⁸ Therefore, the dipole moment gives an approximation of the charge distribution in a system. Hence, it is possible to say that in the rotated dimer systems, there is an inhomogeneous distribution of charges since they are directed from one molecule to the other as observed in Fig. 6b. This is in agreement with the fact that the computed total charges of each molecule are different, for instance, the charge for one of the molecules that constitute the dimer rotated 80° is −0.48 e and the other molecule shows −0.52 e. All these results confirm the displacement of negative charge from one monomer to another one, which occurs for all the rotated systems. However, this is not displayed for the dimers in the eclipsed conformations, as in those cases the charges are equally distributed between the dimers and the magnitude of the dipole moment is zero. Similar results were obtained, when the conformations of one molecule is translated respect to the other. Examples are presented in Fig. 6a and c.

Fig. 6 Calculated dipole moment vectors for representative conformations of the dimers. (a) Eclipsed conformation, (b) rotation 40° and (c) translation t3.

The isosurfaces of the MOs involved in the excitation of the charged dimer are analyzed in order to observe if they are extended across the dimer. This is transcendental since the transitions between orbitals localized separately in each molecule would result in no charge transfer.

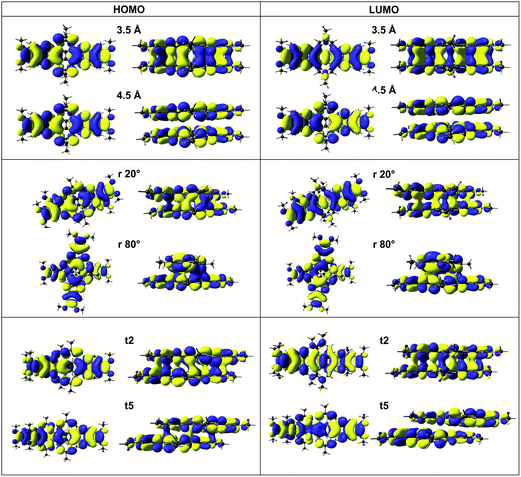
In Fig. 7 are presented the plots of the HOMO and LUMO MOs which are the active orbitals in the calculated lowest energy transition for the eclipsed dimer at 3.5 Å and 4.5 Å. At the shorter separation, these orbitals show bonding character between the orbitals of each monomer, in contrast to the largest separation where no overlap is observed.

Fig. 7 Snapshots of the orbitals involved in the vertical excitation of the −1 charged dimer. The top and side views are presented at 3.5 Å and 4.5 Å separation, rotations of 20° and 80° and translations t2 and t5.

In general, the results show a decrease of π-orbital overlap when the two macrocycles are getting apart as explained above.

Besides, a decrease of the π-orbital overlap is depicted mainly when the rotation between the molecules is around 80° and 100° where the splitting goes down to ∼0.18 eV. In Fig. 7, it is presented the frontier MOs for the rotation of 20° and 80° as well as the translated conformation t2 and t5. Importantly, it is observed that the LUMO orbital is not overlapped when one molecule is moved more than 2 Å respect to the other, thus, it is not suitable for a charge transfer process.

On the other hand, if this study is performed employing the traditional static methodology, it is expected a fast fall of the charge transfer rate with the intermolecular separation or the underestimation of the charge transfer rate when the intermolecular separation increases. As it has been reported for a pentacene dimer, the underestimation could rise a full order of magnitude at distances larger than 5 Å and around 34% at 3.5 Å. A similar behavior is also expected for the other studied conformations since the reason for this observed underestimation errors is due to the lack of re-arrangement of the electronic structure upon the addition of one electron. In conclusion, even though it is expected that the MO geometries are quantitatively unaffected, the MO energies change dramatically employing different methods.

4. Conclusions

The theoretical approach employed in this report allowed studying at molecular level the charge-transfer process that takes place in a π-conjugated systems such as discotic molecules made of bisphenazine derivatives.

Different conformations of bisphenazine dimers were studied such as intermolecular separation, rotation and translation of one monomer respect to the other. Here, the charge transport is able due to the bonding interaction or constructive overlap of the computed isosurfaces of the frontier MOs, which allows the charge movement through the columnar structure formed by the compounds.

Specially, the results highlight that in the eclipsed and lightly displaced geometries, the intermolecular interaction is very pronounced and they show high charge transfer rate which is related to the TD-Split energies. It was observed that in these conformations, the charge is equally distributed and the dipole moment is zero, which could lead to back transfer and a decrease in the efficiency of charge transfer in these conformations.

By the contrary, the rotated systems display a charge displacement from one molecule to the other besides of bonding interactions of the orbitals. This suggests that in this kind of molecules, the best configurations to lead efficient electron transfer are those structures with torsions between the molecules and not the completely faced structure in the column.

Finally, the present work also indicates that quantum-chemical approaches can be useful to get a better knowledge of the structural and geometrical properties of discotic systems.

Acknowledgements

The authors thank to Fondecyt Grant 1130707 and thank to Nicole Mensik for the language corrections.

References

1. (a) S. Kumar, Chemistry of discotic liquid crystals. From monomers to polymers. (Liquid Crystals Book Series), CRC Press Taylor and Francis Group, United States of America, 2011; (b) G. H. Brown and J. J. Wolken, Liquid Crystals and Biological Structures, Academic Press, New York, 1979.
2. (a) S. W. Eaton, L. E. Shoer, S. D. Karlen, S. M. Dyar, E. A. Margulies, B. S. Veldkamp, C. Ramanan, D. A. Hartzler, S. Savikhin, T. J. Marks and M. R. Wasielewski, J. Am. Chem. Soc., 2013, 135(39), 14701–14712; (b) M. Freemantle, Chem. Eng. News, 2002, 80(18), 11; (c) G. Chen, L. Wang, Q. Wang, J. Sun, P. Song, X. Chen, X. Liu, S. Guan, X. Zhang, L. Wang, H. Yang and H. Yu, ACS Appl. Mater. Interfaces, 2014, 6(3), 1380–1384.
3. (a) J. W. Goodby, I. M. Saez, S. J. Cowling, J. S. Gasowska, R. A. MacDonald, S. Sia, P. Watson, K. J. Toyne, M. Hird, R. A. Lewis, S. E. Lee and V. Vaschenko, Liq. Cryst., 2009, 36, 567–605; (b) S. Chandrasekhar and S. Kumar, Sci. Spectra, 1997, 8, 66–72; (c) S. Chen and S. H. Eichhorn, Isr. J. Chem., 2012, 52, 830–843.
4. D. Adam, F. Closs, T. Frey, D. Funhoff, D. Haarer, P. Schuhmacher and K. Siemensmeyer, Phys. Rev. Lett., 1993, 70, 457–460.
5. (a) C. Tschierske, Curr. Opin. Colloid Interface Sci., 2002, 7, 355–370; (b) S. Friberg, in Lyotropic Liquid Crystals, ed. R. F. Gould, Advances in Chemistry Series, American Chemical Society, Washington, DC, 1976; (c) Q. Liu, C. Beier, J. Evans, T. Lee, S. He and I. I. Smalyukh, Langmuir, 2011, 27(12), 7446–7452; (d) S. Chandrasekhar and G. S. Ranganath, Rep. Prog. Phys., 1990, 53, 57–84.
6. (a) L. Criante and F. Scotognella, J. Phys. Chem. C, 2012, 116, 21572–21576; (b) Y. Li, A. Urbas and Q. Li, J. Am. Chem. Soc., 2012, 134, 9573–9576; (c) W. Iglesias, N. L. Abbott, E. K. Mann and A. Jákli, ACS Appl. Mater. Interfaces, 2012, 4, 6884–6890.
7. (a) S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799; (b) F. O. Kannemann and A. D. Becke, J. Chem. Theory Comput., 2010, 6, 1081–1088; (c) J.-W. Song, T. Tsuneda, T. Sato and K. Hirao, Org. Lett., 2010, 12(7), 1440–1443.
8. (a) Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101–194118; (b) Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382.
9. (a) B. Hajgató, S. Güryel, Y. Dauphin, J.-M. Blairon, H. E. Miltner, G. Van Lier, F. De Proft and P. Geerlings, J. Phys. Chem. C, 2012, 116, 22608–22618; (b) Q. Peng, J. W. Pavlik, W. R. Scheidt and O. Wiest, J. Chem. Theory Comput., 2012, 8, 214–223; (c) M. Watanabe, K. Goto, M. Fujitsuka, S. Tojo, T. Majima and T. Shinmyozu, Bull. Chem. Soc. Jpn., 2010, 83(10), 1155–1161; (d) P. A. Denis, J. Phys. Chem. C, 2011, 115, 20282–20288.
10. (a) A. Szabo and N. S. Ostlund, Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory. McGraw-Hill Publishing Company, New York, 1989; (b) E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034.
11. (a) J. L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5003; (b) X. Zarate, E. Schott, L. Alvarado-Soto and T. C. Sutherland, Int. J. Quantum Chem., 2013, 113, 2287–2294; (c) V. Lemaur, D. A. da Silva Filho, V. Coropceanu, M. Lehmann, Y. Geerts, J. Piris, M. G. Debije, A. M. van de Craats, K. Senthilkumar, L. D. A. Siebbeles, J. M. Warman, J. L. Brédas and J. Cornil, J. Am. Chem. Soc., 2004, 126, 3271–3279; (d) T. Stein, L. Kronik and R. Baer, J. Am. Chem. Soc., 2009, 131, 2818–2820; (e) H. N. Chen, M. A. Ratner and G. C. Schatz, J. Phys. Chem. C, 2011, 115, 18810–18821.
12. (a) R. Reslan, K. Lopata, C. Arntsen, N. Govind and D. Neuhauser, J. Chem. Phys., 2012, 137, 22A502; (b) L. A. Bartell, R. Reslan, M. R. Wall, R. D. Kennedy and D. Neuhauser, Chem. Phys., 2011, 391, 62–68.
13. (a) C.-P. Hsu, Acc. Chem. Res., 2009, 42, 509–518; (b) G. Kestemont, V. de Halleux, M. Lehmann, D. A. Ivanov, M. Watson and Y. H. Geerts, Chem. Commun., 2001, 2074–2075.
14. (a) A. E. Murschell and T. C. Sutherland, Langmuir, 2010, 26(15), 12859–12866; (b) A. D. Bromby, W. H. Kan and T. C. Sutherland, J. Mater. Chem., 2012, 22, 20611–20617; (c) H. S. Kim, J. H. Lee, T. H. Kim, S. Okabe, M. Shibayama and S. M. Choi, J. Phys. Chem. B, 2011, 115, 7314–7320; (d) B. Roy, N. De and K. C. Majumdar, Chem.–Eur. J., 2012, 18, 14560–14588; (e) S. Leng, L. H. Chan, J. Jing, J. Hu, R. M. Moustafa, R. M. Van Horn, M. J. Graham, B. Sun, M. Zhu, K. U. Jeong, B. R. Kaafarani, W. Zhang, F. W. Harris and S. Z. D. Cheng, Soft Matter, 2010, 6, 100–112; (f) G. Kestemont, V. de Halleux, M. Lehmann, D. A. Ivanov, M. Watson and Y. H. Geerts, Chem. Commun., 2001, 2074–2075.
15. (a) D. C. Lee, K. Jang, K. K. McGrath, R. Uy, K. A. Robins and D. W. Hatchett, Chem. Mater., 2008, 20, 3688–3695; (b) J. Hu, D. Zhang, S. Jin, S. Z. D. Cheng and F. W. Harris, Chem. Mater., 2004, 16, 4912–4915.
16. A. Fonari, F. M. Jradi, M. S. Fonari, M. H. Al-Sayah, M. Yu. Antipin, B. R. Kaafarani and T. V. Timofeeva, J. Mol. Struct., 2011, 996, 141–147.
17. K. Nakayama, Y. Hashimoto, H. Sasabe, Y. J. Pu, M. Yokoyama and J. Kido, Jpn. J. Appl. Phys., 2010, 49, 01AB11.
18. F. S. Raad, A. O. El-Ballouli, R. M. Moustafa, M. H. Al-Sayah and B. R. Kaafarani, Tetrahedron, 2010, 66, 2944–2952.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
20. V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976–984.
21. (a) E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000; (b) A. Zangwill and P. Soven, Phys. Rev. A, 1980, 21, 1561–1572.
22. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
23. C. P. Hsu, Acc. Chem. Res., 2009, 42, 509–518.
24. (a) J. Hernández-Trujillo, I. García-Cruz and J. M. Martínez-Magadán, Chem. Phys., 2005, 308, 181–192; (b) I. García-Cruz, J. M. Martínez-Magadán, J. M. Bofill and F. Illas, J. Phys. Chem. A, 2004, 108, 5111–5116; (c) A. K. Kandalam, P. Jena, X. Li, S. N. Eustis and K. H. Bowen, J. Chem. Phys., 2008, 129, 134308/1–134308/11.
25. B. Z. Yang, X. Zhou, T. Liu, F. Q. Bai and H. X. Zhang, Int. J. Quantum Chem., 2011, 111, 2258–2267.
26. (a) K. A. Robins, K. Jang, B. Cao and D. C. Lee, Phys. Chem. Chem. Phys., 2010, 12, 12727–12733; (b) K. K. McGrath, K. Jang, K. A. Robins and D. C. Lee, Chem.–Eur. J., 2009, 15, 4070–4077.
27. R. Moustafa, Synthesis of pyrene-based discotics for potential electronic applications, American University of Beirut, Beirut, Lebanon, 2008.
28. (a) F. Sim, D. R. Salahub and S. Chin, Int. J. Quantum Chem., 1992, 43, 463–419; (b) K. Hu, K. C. D. Robson, E. E. Beauvilliers, E. Schott, X. Zarate, R. Arratia-Perez, C. P. Berlinguette and G. J. Meyer, J. Am. Chem. Soc., 2014, 136(3), 1034–1046.

---