Experimental design and multi-objective optimization of molecularly imprinted polymers for monosaccharides†
A. Mirmohseni*a,
M. Shojaeib and
R. Pouratac
aPolymer Research Technology Laboratory, Department of Applied Chemistry, Faculty of Chemistry, University of Tabriz, Iran. E-mail: mirmohseni@tabrizu.ac.ir; Fax: +98-411-3340191; Tel: +98-411-3393171
bAnimal Science Group, Faculty of Natural Sciences, University of Tabriz, Iran. E-mail: mshojaei@tabrizu.ac.ir
cPolymer Research Technology Laboratory, Department of Applied Chemistry, Faculty of Chemistry, University of Tabriz, Iran. E-mail: r_pourata@yahoo.com
First published on 24th April 2014
Abstract
The Taguchi method was used as an experimental design and optimization tool for the preparation of monosaccharide molecularly imprinted polymers (MIPs). Three factors, namely type of functional monomer, molar percentage of functional monomer, and functional monomer to template molar ratio, were included in the experimental design and based on the L16 (43) array, four levels of each factor were chosen. Imprinting factor, selectivity, and equilibration time were considered as quality characteristics of MIPs. For quantitative assessment of the quality of the prepared MIPs, the adsorption of template and competing substance on the prepared MIPs and non-imprinted polymers was monitored by the quartz crystal nanobalance (QCN) technique. The results revealed that regarding each quality characteristic, there are different optimal levels of the factors. The principal component analysis (PCA) technique was used to combine the quality characteristics in order to obtain a single characteristic for overall optimization of monosaccharide MIPs performance. So, PCA coupled with the Taguchi method was developed as an efficient procedure to optimize monosaccharide MIPs. The optimum values of molar percentage of functional monomer and the functional monomer to template molar ratio were found to be 30 and 4, respectively. We also found that acrylic acid (AAc) is a favourable functional monomer for preparing monosaccharide MIPs.
1 Introduction
Molecular imprinting is a useful technique to synthesize polymers with selective recognition properties.1–4 Molecularly imprinted polymers (MIPs) have proved themselves to be useful in solid-phase extraction,5 chromatography,6 pharmaceutical analysis,7 immunoassay,8 chiral separation,9 and quartz crystal nanobalance (QCN)-based sensors.10–15 In order to prepare an MIP, template and a proper monomer are mixed to form a functional monomer–template complex in solution and then the process is pursued by polymerization and solidification. By removing the template from the polymer, the obtained cavities are specific for the template and act as specialized receptors of the template that are complementary in size, shape, and functional groups orientation to the imprinted template. Upon exposing an MIP to media containing target (template) species, targets are selectively adsorbed on the MIP as a result of rebinding interactions between organized functional groups of the cavities and target molecules.16There are many reports in the literature on the optimization of MIP preparation process to improve their adsorption capacity, imprinting factor (IF), adsorption selectivity, and other quality characteristics such as the time required for equilibrated distribution of the target species between MIP and target-containing medium. This latter characteristic is usually used to evaluate performance quality of MIPs in some application fields such as making sensors and solid-phase microextraction. The performance of MIPs is influenced by several experimental variables including type of functional monomer, the ratio of functional monomer to template, functional monomer percentage, and type of solvent.5,17–20
Yao and co-workers18 applied computational design to investigate optimal conditions for aniline MIP synthesis. Adsorption of aniline was used to evaluate the performance of MIP which revealed that functional monomer type and solvent are effective variables in the synthesis of the aniline MIPs. In another study, the influence of cross-linker percentage and the length of cross-linking agent on affinity, adsorption capacity, and selectivity have been investigated for testosterone MIP.21 Caballero et al.22 used computational modelling for the selection of functional monomer and monomer–template ratio in order to prepare chiral imprinted polymers as enantio-specific coatings. They found that acrylamide is suitable functional monomer for synthesis of (S)-citalopram MIP and proper monomer–template ratio is 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Golsefidi et al.23 prepared an MIP for chlorogenic acid. They studied the ratio of functional monomer to cross-linker, molar ratio of template to functional monomer, and carbon nanotube percentage as effective parameters in MIP performance.
1. Golsefidi et al.23 prepared an MIP for chlorogenic acid. They studied the ratio of functional monomer to cross-linker, molar ratio of template to functional monomer, and carbon nanotube percentage as effective parameters in MIP performance.
With the aim of selecting suitable functional monomer, a methodology based on screening library for non-imprinted polymer (NIP) has been developed.24 4-Vinylpryridine has been found as the best functional monomer among several functional monomers for preparing amiodarone MIP. In another study, the influence of molar ratio of functional monomer to template and to cross-linker, solvent type, and the amount of solvent have been discussed on the performance of caffeine MIP.25
Taguchi method is a usual experimental design technique for optimization of chemical and chemical engineering processes.4,26,27 This method is also employed to find out conditions leading to a product with enhanced characteristics or quality.28,29 Mehdinia et al.30 used Taguchi method for the optimization of magnetic MIP synthesis conditions. Amount of modified Fe3O4–SiO2, the ratio of template to monomer, and the molar ratio of monomer to cross-linker were considered as the most effective parameters. The adsorption capacity of magnetic molecularly imprinted polymers was measured as the response. Mijangos et al.31 used a chemometrics approach to investigate the effect of polymerization condition on MIP performance. However, such a single-objective optimization of MIP cannot guarantee enhancement of its other characteristics such as selectivity.
S. Kunath et al.32 employed a multi-objective optimization method to improve the overall performance of glucuronic acid MIP. They used full factorial experimental design with 3 factors at 2 levels to optimize four properties of MIP. A desirability value was defined for each property of the MIP and the geometrical mean of desirability values was used as overall single property for MIP performance optimization. This study is the first report on multi-objective optimization of MIPs however; it seems that in order to performance a good multi-objective optimization, the combination of uncorrelated variables can be more suitable than the combination of probably correlated variables (properties of MIP).
Some reports showed that combination of Taguchi with principal component analysis (PCA) method could be used as a practical and effective approach towards multi-response problem optimization.33,34 It seems that this method can also be useful in determining factors effects and their optimum levels to achieve the best MIP performance.
Traditionally, in order to evaluate the performance of MIPs, the adsorption of template to the MIPs is investigated after equilibrium. However, it seems that monitoring the adsorption of template to MIP during the time might be useful for MIP performance evaluation, especially in using them in sensors and catalysts. In this regards, QCN technique can be used as a suitable method to investigate performance of MIP.
In this study, in order to prepare an optimized glucose MIP, the L16 (43) experimental design was performed according to Taguchi method. Three factors, namely functional monomer type, molar percentage of functional monomer with respect to total monomer (functional monomer plus cross-linker), and molar ratio of functional monomer to template were included in the optimization. IF, selectivity of the MIP, and its equilibration time, which were determined by QCN technique, were individually optimized as MIP characteristics. Furthermore, PCA method was used to obtain an overall characteristic parameter for optimization of glucose MIPs' performance.
As Fig. 1 shows, glucose, galactose, and fructose have similar molecular structures. The only difference between them is in the arrangement of a few atoms.35 So, the obtained optimum condition for the preparation of glucose MIP was used to prepare the MIPs for galactose and fructose. To the best of the authors' knowledge, this is the first report on the optimization of MIP as a multi-objective problem using combination of Taguchi and PCA method.
 | ||
| Fig. 1 Molecular structure of glucose, galactose, and fructose.35 | ||
2 Experimental
2.1 Reagents and materials
All utilized chemicals were of analytical-reagent grade. Poly(vinyl chloride) (PVC) was obtained from Sigma Aldrich Co. Ethylene glycol dimethacrylate (EGDMA), acrylamide (AAm), acrylic acid (AAc), allyl alcohol (AAl), acrylonitrile (AN), dimethyl sulfoxide (DMSO), tetrahydrofuran (THF) and 2,2′-azobisisobutyronitrile (AIBN) were purchased from Merck (Germany) and used without any further purification.2.2 Instrumentation
10 MHz AT-Cut quartz crystals with gold coating on both sides were supplied by International Crystal Manufacturer (ICM, OK, USA). For QCN experiments, a homemade apparatus was used as described in our previous work.36 The employed oscillator circuit was according to Bruckenstein and Shay's design;37 however, some modifications of the original design were made to improve mass sensitivity and stability.38 All measurements were carried out in a flow cell with an internal volume of 0.15 mL.2.3 Preparation of modified quartz crystal
In situ preparation of the MIP was carried out as follows: according to Table 1, certain amounts of functional monomer and template were dissolved in 5 mL DMSO and the mixture was stirred for 1 h. Then, a desired amount of EGDMA and 0.005 g of AIBN were added to the solution. Sum of number of functional monomer and EGDMA moles in each synthesis was 0.005 mol. Next, nitrogen gas was sparged into the mixture for 15 min to remove any dissolved oxygen. Polymerization reaction was initiated by heating at 60 °C for 12 h. Obtained bulk polymers were grounded and washed by water to remove non-polymerized monomers and the solvent. In the same vein, NIPs were prepared using exactly the above procedure without including the template.| Trial no. | Factors | Quality characteristicsa | ||||
|---|---|---|---|---|---|---|
| FM | FM% | FM/T | IF | Selectivity | Equilibration time (min) | |
| a Mean of 3 replicates ± 2 × standard deviation. | ||||||
| 1 | AAm | 20 | 2 | 8.48 ± 0.46 | 3.65 ± 0.011 | 84 ± 3 |
| 2 | AAm | 30 | 4 | 10.36 ± 0.32 | 5.23 ± 0.14 | 65 ± 3 |
| 3 | AAm | 40 | 6 | 8.10 ± 0.31 | 4.95 ± 0.16 | 72 ± 3 |
| 4 | AAm | 50 | 8 | 3.83 ± 0.16 | 3.25 ± 0.08 | 76 ± 2 |
| 5 | AAc | 20 | 4 | 10.57 ± 0.50 | 5.60 ± 0.23 | 100 ± 4 |
| 6 | AAc | 30 | 2 | 9.52 ± 0.37 | 3.08 ± 0.10 | 56 ± 2 |
| 7 | AAc | 40 | 8 | 7.53 ± 0.25 | 5.91 ± 0.18 | 77 ± 3 |
| 8 | AAc | 50 | 6 | 4.97 ± 0.26 | 4.07 ± 0.11 | 64 ± 4 |
| 9 | AAl | 20 | 6 | 5.04 ± 0.31 | 4.44 ± 0.21 | 116 ± 4 |
| 10 | AAl | 30 | 8 | 3.28 ± 0.34 | 4.62 ± 0.14 | 106 ± 2 |
| 11 | AAl | 40 | 2 | 4.27 ± 0.29 | 2.22 ± 0.05 | 60 ± 3 |
| 12 | AAl | 50 | 4 | 3.29 ± 0.25 | 2.34 ± 0.08 | 49 ± 2 |
| 13 | AcN | 20 | 8 | 3.05 ± 0.13 | 2.94 ± 0.11 | 181 ± 5 |
| 14 | AcN | 30 | 6 | 4.07 ± 0.34 | 2.89 ± 0.13 | 125 ± 3 |
| 15 | AcN | 40 | 4 | 3.82 ± 0.29 | 1.92 ± 0.04 | 68 ± 2 |
| 16 | AcN | 50 | 2 | 2.1 ± 0.24 | 1.26 ± 0.02 | 69 ± 3 |
The ground polymer particles were dispersed in a solution of 1% PVC (the binder) in THF. The ratio of MIP powder to PVC was 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 (w/w). In order to coat quartz crystal, a certain amount (2 μL) of the solution was dropped on top of the gold electrode of the quartz crystal. Next, the solvent was evaporated at 60 °C for 24 h and a thin film of the polymer was obtained on the electrode surface. Using constant amount and concentration of coating solution leads to a reproducible frequency shift of approximately 22 kHz for all modifications of crystals. Finally, in order to remove the template, the coated crystal was washed with 5% (v/v) methanol for 5 h.
50 (w/w). In order to coat quartz crystal, a certain amount (2 μL) of the solution was dropped on top of the gold electrode of the quartz crystal. Next, the solvent was evaporated at 60 °C for 24 h and a thin film of the polymer was obtained on the electrode surface. Using constant amount and concentration of coating solution leads to a reproducible frequency shift of approximately 22 kHz for all modifications of crystals. Finally, in order to remove the template, the coated crystal was washed with 5% (v/v) methanol for 5 h.
2.4 Procedures
The monosaccharides standard stock solutions were prepared by dissolving 1000 mg of each monosaccharide in 1 L distilled water. The stock solutions were prepared 24 h before use, in order to establish the anomeric equilibrium, and were then stored in refrigerator. Fresh stock solutions were prepared weekly. In order to measure the characteristics of MIPs, a peristaltic pump was used to drive samples through the flow cell at the rate of 0.5 mL min−1 and frequency shift of crystal was recorded every second. Before injection of monosaccharide solution, coated crystal was exposed to the blank solution (distilled water) until the frequency of crystal was fixed and a steady state was reached. After each measurement, washing solution (5% methanol) was pumped through the flow cell for 0.5 h to remove the adsorbed monosaccharide from coated quartz crystals.2.5 Taguchi method
| Experimental factors | Levels | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| A: Functional monomer (FM) | AAm | AAc | AAl | AcN |
| B: Functional monomer percent (FM %) | 20 | 30 | 40 | 50 |
| C: Functional monomer/Template (FM/T) | 2 | 4 | 6 | 8 |
According to the Sauerbrey equation, resonance frequency shift of the quartz crystal is directly proportional to the mass deposited on quartz surface.41 Therefore, frequency shift of the MIP-coated quartz crystal exposed to template solution is in proportion with the adsorbed amount of template on the coated-MIP.
IF which indicates imprinting quality of the synthesized MIPs was calculated by the following equation:
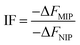 | (1) |
Selectivity of MIP can be calculated by the following equation:
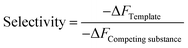 | (2) |
Fig. 2 shows frequency shift of quartz crystal and its first derivative versus time as exposed to the template solution. It is clear from this figure that the rate of template adsorption is very fast during the initial stage after sample injection and with the passage of time it is significantly reduced. It can be assumed that, when the slope of the response curve of MIP-coated quartz crystal is less than 1% of its initial amount, the equilibrium of adsorption is practically achieved. To obtain the slope of the QCN response curve, it was fitted to a polynomial of third degree with respect to time and in form of the following equation:
| −ΔF(t) = a3t3 + a2t2 + a1t + a0 | (3) |
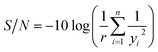 | (4) |
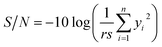 | (5) |
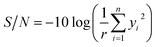 | (6) |
The average effect of factors was used to investigate factor effects on quality characteristics and to estimate the optimum conditions. The average effect of a factor, say A, at one of its levels, say Ai, is calculated adding together the S/N values corresponding to trials at which A was set at level Ai and dividing the obtained sum by number of the trials.42 The analysis of variance (ANOVA) was also used to evaluate the influence of each factor on the quality characteristics.43
2.6 Principal component analysis
PCA involves a mathematical procedure that transforms a set of possibly correlated variables into a set of independent principal components (PCs).44 So, it is possible to convert a set of responses or quality characteristics (e.g. in a multi-objective process) to a set of PCs using PCA. The PCA was performed as follows:34,45(1) Quality characteristics matrix was created for three quality characteristics and n trials.
(2) The quality characteristics were normalized using the following equation:
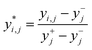 | (7) |
(3) The eigenvalues and eigenvectors of the correlation coefficient of the normalized quality characteristics matrix were calculated.
(4) The principal components of normalized quality characteristics matrix were obtained as follows:
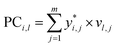 | (8) |
(5) The total principal component index (TPCI) was used as overall performance characteristic corresponding to each trial in order to evaluate the effect of factors and to find optimum level of each factor. TPCI was calculated as follows:
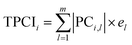 | (9) |
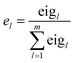 | (10) |
3 Results and discussion
3.1 Evaluation of effect of factors on quality characteristics
Obtained quality characteristics (Table 1) were normalized and then converted to the S/N ratio using eqn (4)–(6). The S/N values for IF and selectivity were calculated using eqn (4) (larger-the-better). Also, eqn (6) (smaller-the-better) was used to obtain the S/N values for equilibration time. The S/N values for all quality characteristics were presented in Table 3.| Trial no. | S/N of quality characteristics (db) | ||
|---|---|---|---|
| IF | Selectivity | Equilibration time | |
| 1 | 18.5600 | 11.2509 | −38.5217 |
| 2 | 20.3033 | 14.3732 | −36.2166 |
| 3 | 18.1694 | 13.8830 | −37.1489 |
| 4 | 11.6476 | 10.2445 | −37.5793 |
| 5 | 19.6437 | 14.9533 | −40.0020 |
| 6 | 19.5712 | 9.7579 | −34.9141 |
| 7 | 17.0351 | 15.4337 | −37.7318 |
| 8 | 13.5316 | 12.1967 | −36.1731 |
| 9 | 14.0392 | 12.9339 | −41.3154 |
| 10 | 10.2765 | 13.2963 | −40.4794 |
| 11 | 12.5873 | 6.9255 | −35.5182 |
| 12 | 10.3479 | 7.3927 | −33.7475 |
| 13 | 8.5131 | 9.3621 | −45.1544 |
| 14 | 12.1626 | 9.2218 | −41.9389 |
| 15 | 11.6229 | 5.6796 | −36.6090 |
| 16 | 5.2192 | 1.9837 | −36.7376 |
Fig. 3 shows the effects of individual factors including functional monomer type (FM), functional monomer molar percentage (FM%), and molar ratio of functional monomer to template (FM/T) on each quality characteristic. The findings showed that the MIPs synthesized using AAc in comparison to the other synthesized MIPs resulted in the largest IF and selectivity. Also regarding equilibration time, poly(AAc-co-EGDMA) had better performance than the other synthesized MIPs. These results may be explained in terms of stronger interactions of hydroxyl groups of glucose with AAc.18
 | ||
| Fig. 3 Effects of factors on S/N for (a): IF, (b): selectivity, and (c): equilibration time (obtained from glucose MIP-modified quartz crystal). | ||
It is clear from Fig. 3 that an increase in functional monomer percentage leads to increase in the IF and decrease in the equilibration time. It is due to increase in adsorption sites and water compatibility of polymers. However, when the functional monomer increases to more than 30%, IF is decreased. It is probably due to the instability of imprinted cavities because of the reduction of cross-linking degree. On the other hand, selectivity of the MIPs reduced by increasing functional monomer percentage because the mobility of the polymer network increased by reduction of cross-linking degree of MIPs.
Increasing molar ratio of the functional monomer to the template is favorable regarding selectivity of the MIP and unfavorable with regard to the equilibration time. However, after level 3 (FM/T = 6), any further increase in the molar ratio had no effect on selectivity of the MIP. It is probably due to the fact that although addition of functional groups around the adsorption cavities leads to highly selective MIP, template transfer into or out of theses cavities is difficult.
Fig. 3 also demonstrates that S/N value for each quality characteristic was optimized at different factor–level combinations. The factor–level combinations A2B2C2, A2B1C4, and A2B4C1 were found as the favorable factor–level combination for the IF, selectivity, and equilibration time, respectively. A, B, and C denote functional monomer type, functional monomer molar percentage, and molar ratio of functional monomer to template, respectively and the subscript numbers represent the level of each factor.
The results of ANOVA for each quality characteristic are given in Table 4. The contribution of factors in increasing order is functional monomer type, functional monomer molar percentage, and functional monomer to template molar ratio for IF and selectivity. However, for equilibration time, this order changes to functional monomer molar percentage, functional monomer to template molar ratio, and functional monomer type. Moreover, the F ratio of each factor represents its significance.
| Response | Factors | DOF | S | V | F | S′ | P% |
|---|---|---|---|---|---|---|---|
| IF | FM | 3 | 192.18 | 64.06 | 85.20 | 189.92 | 63.06 |
| FM% | 3 | 76.67 | 25.56 | 33.99 | 74.41 | 24.71 | |
| FM/T | 3 | 27.80 | 9.27 | 12.33 | 25.55 | 8.48 | |
| Error | 6 | 4.51 | 0.75 | 3.74 | |||
| Total | 15 | 301.16 | 100 | ||||
| Selectivity | FM | 3 | 104.27 | 34.76 | 29.20 | 100.70 | 48.07 |
| FM% | 3 | 41.84 | 13.95 | 11.72 | 38.27 | 18.27 | |
| FM/T | 3 | 56.24 | 18.75 | 15.75 | 52.67 | 25.14 | |
| Error | 6 | 7.14 | 1.19 | 8.52 | |||
| Total | 15 | 209.50 | 100 | ||||
| Equilibration time | FM | 3 | 21.96 | 7.32 | 9.76 | 19.71 | 14.85 |
| FM% | 3 | 63.90 | 21.30 | 28.41 | 61.65 | 46.46 | |
| FM/T | 3 | 42.34 | 14.11 | 18.83 | 40.10 | 30.21 | |
| Error | 6 | 4.50 | 0.75 | 8.47 | |||
| Total | 15 | 132.71 | 100 |
It can be seen that the significance of factors and optimal factor–level combination for quality characteristics were different. Therefore, combination of quality characteristics using PCA method was considered as a suitable technique to obtain an overall performance characteristic for evaluation of the optimum conditions and the importance of effective factors in MIP preparation process.
3.2 Overall optimization of glucose MIP
In multi-objective problems, it is possible that the optimum condition be different for each objective. In order to obtain a individual conditions, it is necessary to combine the objectives. In this study there were three quality characteristics used for MIPs characterization and the PCA method was employed to combine them. The eigenvalues and eigenvectors corresponding to the correlation coefficient matrix are tabulated in Table S1 (ESI†).The TPCI was used as a single performance characteristic corresponding to each trial for evaluation and optimization of factors. In fact TPCI is the weighted sum of absolute value of principal components that related to quality characteristics of experimental run. Table 5 shows three principal components and TPCI for each trial obtained using eqn (8)–(10).
| Trial | PC1 | PC2 | PC3 | TPCI |
|---|---|---|---|---|
| 1 | −1.0542 | 0.6445 | −0.0770 | 0.8436 |
| 2 | −1.2925 | 0.8200 | −0.2155 | 1.0528 |
| 3 | −1.1667 | 0.7100 | −0.2652 | 0.9437 |
| 4 | −0.6540 | 0.5942 | −0.3765 | 0.6148 |
| 5 | −1.3542 | 0.5157 | −0.1323 | 0.9719 |
| 6 | −1.0032 | 0.9706 | −0.0541 | 0.9320 |
| 7 | −1.2212 | 0.6301 | −0.3569 | 0.9515 |
| 8 | −0.8614 | 0.7247 | −0.4069 | 0.7831 |
| 9 | −0.9373 | 0.3100 | −0.2963 | 0.6684 |
| 10 | −0.7659 | 0.2959 | −0.5140 | 0.5787 |
| 11 | −0.5116 | 0.8210 | −0.2227 | 0.6064 |
| 12 | −0.4154 | 0.9099 | −0.4000 | 0.5949 |
| 13 | −0.5548 | −0.0334 | −0.2159 | 0.3434 |
| 14 | −0.6510 | 0.2730 | −0.1808 | 0.4837 |
| 15 | −0.4043 | 0.7320 | −0.1753 | 0.5095 |
| 16 | 0.0502 | 0.6665 | −0.2322 | 0.2864 |
The results of ANOVA for TPCI were shown in Table 6. The results showed the contribution of error was less than 5%. Furthermore the calculated variance ratios (F value) for the investigated factors are greater than 4.76 which was determined from the standard F table at 95% significance level and this indicated that the factors are meaningful at 95% significance level for glucose–MIP optimization. Fig. 4 shows that the S/N for TPCI was maximized in A2B2C2 factor–level combination. It is clear from the results that the optimal values of functional monomer molar percentage and functional monomer to template molar ratio are 30 and 4, respectively. It, also, reveals that AAc is the most suitable functional monomer for monosaccharide MIP preparation.
| Factors | DOF | S | V | F | S′ | P% |
|---|---|---|---|---|---|---|
| FM | 3 | 0.6601 | 0.2200 | 89.61 | 0.6527 | 78.99 |
| FM% | 3 | 0.0943 | 0.0314 | 12.80 | 0.0869 | 10.52 |
| FM/T | 3 | 0.0571 | 0.0191 | 7.76 | 0.0498 | 6.03 |
| Error | 6 | 0.0147 | 0.0025 | 4.46 | ||
| Total | 15 | 0.8263 | 100 |
3.3 Performance of optimized MIPs
With regard to glucose, galactose and fructose are similar in molecular structure and functional groups therefore it seems that the optimum conditions of MIP preparation for glucose and other monosaccharide should be similar. So the MIPs for glucose, galactose, and fructose were prepared along with NIP using optimum condition determined in Section 3.2. The synthesized co-polymers were coated on the quartz crystals and exposed to the solutions of glucose, galactose, and fructose. Frequency shift, selectivity, IF, and equilibration time of prepared MIPs were given in Table 7. The results indicated that the obtained conditions can be successfully employed for monosaccharide MIPs.| Quality characteristics | Glucose MIP | Galactose MIP | Fructose MIP | NIP | |
|---|---|---|---|---|---|
| −ΔF (Hz) for solution of | Glucose | 131 | 23 | 25 | 14 |
| Galactose | 26 | 135 | 24 | 14 | |
| Fructose | 21 | 23 | 142 | 14 | |
| Selectivity (against competing substance) | Glucose | — | 5.7 | 5.24 | — |
| Galactose | 5.19 | — | 5.62 | — | |
| Fructose | 6.76 | 6.17 | — | — | |
| IF | 9.35 | 9.64 | 10.14 | — | |
| Equilibration time (min) | 61 | 63 | 60 | 42 | |
4 Conclusions
In this study, Taguchi method and PCA coupled with Taguchi were found to be useful experimental design and optimization methods for monosaccharide MIPs polymerization whether they get treated as single-objective problems or as multi-objective problem. The results showed that optimum conditions for MIP preparation and order of significance of factors were different in single-objective optimization. Factor–level combination A2B2C2, A2B1C4, and A2B4C1 were found to be favorable regarding IF, selectivity, and equilibration time, respectively.Overall performance optimization of monosaccharide MIP preparation was successfully performed using PCA coupled with Taguchi method. Based on ANOVA results, contributions of factors were 79, 10.5, and 6 for functional monomer type, functional monomer molar percentage, and functional monomer to template molar ratio, respectively. The factor–level combination for the best overall performance of monosaccharide MIP was found to be A2B2C2. The results also proved that QCN technique can be employed as a useful tool for investigating performance of MIP.
Acknowledgements
The authors would like to express their gratitude to the University of Tabriz for financially supporting this research project.References
- H. Zhou, G. Xu, A. Zhu, Z. Zhao, C. Ren, L. Nie and X. Kan, RSC Adv., 2012, 2, 7803–7808 RSC.
- W. M. Mullett, M. F. Dirie, E. P. C. Lai, H. Guo and X. He, Anal. Chim. Acta, 2000, 414, 123–131 CrossRef CAS.
- X. B. Zhang, J. Li, B. You, G. P. Yong, H. W. Tong and S. M. Liu, RSC Adv., 2012, 2, 9778–9780 RSC.
- S. Pradhan, M. Boopathi, O. Kumar, A. Baghel, P. Pandey, T. H. Mahato, B. Singh and R. Vijayaraghavanand, et al., Biosens. Bioelectron., 2009, 25, 592–598 CrossRef CAS PubMed.
- A. L. Jenkins, M. W. Ellzy and L. C. Buettner, J. Mol. Recognit., 2012, 25, 330–335 CrossRef CAS PubMed.
- Y. Xie, D. Chen, J. Zhao, Y. Peng, N. Jiang, X. Zhou, S. Du and Z. Zhang, RSC Adv., 2012, 2, 273–283 RSC.
- Z. Wang, J. Ouyanga and W. R. G. Baeyens, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2008, 862, 1–14 CrossRef CAS PubMed.
- S. A. Piletsky, E. V. Piletska, A. Bossi, K. Karim, P. Lowe and A. P. F. Turneret, Biosens. Bioelectron., 2001, 16, 701–707 CrossRef CAS.
- R. J. Ansell, Adv. Drug Delivery Rev., 2005, 57, 1809–1835 CrossRef CAS PubMed.
- Y. Fu and H. O. Finklea, Anal. Chem., 2003, 75, 5387–5393 CrossRef CAS.
- F. Liu, X. Liu, S. C. Ng and H. S. O. Chan, Sens. Actuators, B, 2006, 113, 234–240 CrossRef CAS PubMed.
- Z. P. Yang and C. J. Zhang, Sens. Actuators, B, 2009, 142, 210–215 CrossRef CAS PubMed.
- M. Shojaei, A. Mirmohseni and M. Farbodi, Anal. Bioanal. Chem., 2008, 391, 2875–2880 CrossRef CAS PubMed.
- T. Y. Lin, C. H. Hub and T. C. Choub, Biosens. Bioelectron., 2004, 20, 75–81 CrossRef CAS PubMed.
- A. H. Wu and M. J. Syu, Biosens. Bioelectron., 2006, 21, 2345–2353 CrossRef CAS PubMed.
- R. Say, A. Gultekin and A. A. Ozcan, et al., Anal. Chim. Acta, 2009, 640, 82–86 CrossRef CAS PubMed.
- I. A. Nicholls, H. S. Andersson and K. Golker, et al., Anal. Bioanal. Chem., 2011, 400, 1771–1787 CrossRef CAS PubMed.
- J. Yao, X. Li and W. Qin, Anal. Chim. Acta, 2008, 610, 282–288 CrossRef CAS PubMed.
- I. A. Nicholls, H. S. Andersson and C. Charlton, et al., Biosens. Bioelectron., 2009, 25, 543–552 CrossRef CAS PubMed.
- I. A. Nicholls, B. C. G. Karlsson, G. D. Olsson and A. M. Rosengren, Ind. Eng. Chem. Res., 2013, 52, 13900–13909 CrossRef CAS; A. L. Jenkins, M. W. Ellzy and L. C. Buettner, J. Mol. Recognit., 2012, 25, 330–335 CrossRef PubMed.
- K. R. Noss, A. D. Vaughan and M. E. Byrne, J. Appl. Polym. Sci., 2008, 107, 3435–3441 CrossRef CAS.
- A. Gomez-Caballero, A. Guerreiro, K. Karim, S. Piletsky, M. A. Goicolea and R. J. Barrio, Biosens. Bioelectron., 2011, 28, 25–32 CrossRef CAS PubMed.
- M. A. Golsefidi, Z. Es'haghi and A. Sarafraz-Yazdi, J. Chromatogr. A, 2012, 1229, 24–29 CrossRef CAS PubMed.
- T. Muhammad, L. Cui, W. Jide, E. V. Piletska, A. R. Guerreiro and S. A. Piletsky, Anal. Chim. Acta, 2012, 709, 98–104 CrossRef CAS PubMed.
- K. Farrington, E. Magner and F. Regan, Anal. Chim. Acta, 2006, 566, 60–68 CrossRef CAS PubMed.
- A. Asghari, M. Kamalabadi and H. Farzinia, Chem. Biochem. Eng. Q., 2012, 26, 145–154 CAS.
- S. S. Madaeni and S. Koocheki, Chem. Eng. J., 2006, 119, 37–44 CrossRef CAS PubMed.
- M. Kaladhar, K. V. Subbaiah, C. Srinivasa Rao and K. Narayana Rao, J. Eng. Sci. Technol. Rev., 2011, 4, 55–61 CrossRef.
- A. A. Mohamed, Y. Hafizal, A. Sahrim, R. Rozaidi, A. Jaafar, M. Dahlan, M. A. M. Harun, M. Mahathir and M. H. Harun, Journal of Nuclear and Related Technologies, 2012, 9, 23–32 Search PubMed.
- A. Mehdinia, T. Baradaran Kayyal, A. Jabbari, M. O. Aziz-Zanjani and E. Ziaei, J. Chromatogr. A, 2013, 1283, 82–88 CrossRef CAS PubMed.
- I. Mijangos, F. N. Villoslada, A. Guerreiro, E. Piletska, I. Chianella, K. Karim, A. Turner and S. Piletsky, Biosens. Bioelectron., 2006, 22, 381–387 CrossRef CAS PubMed.
- S. Kunath, N. Marchyk, K. Haupt and K. H. Feller, Talanta, 2013, 105, 211–218 CrossRef CAS PubMed.
- J. Antony, Int. J. Reliab. Qual. Saf. Eng., 2000, 16, 3–8 CrossRef.
- C. P. Fung and P. C. Kang, J. Mater. Process. Technol., 2005, 170, 602–610 CrossRef CAS PubMed.
- R. K. Murray, D. A. Bender, K. M. Botham, P. J. Kennelly, V. W. Rodwell and P. A. Weil, Harper's Illustrated Biochemistry, McGraw-Hill Companies, US, 26th edn, 2003, pp. 103–104 Search PubMed.
- A. Mirmohseni, M. Milani and V. Hassanzadeh, Polym. Int., 1999, 48, 873–878 CrossRef CAS.
- S. Bruckenstein and M. Shay, Electrochim. Acta, 1985, 30, 1295–1300 CrossRef CAS.
- A. Mirmohseni, Ph.D. Thesis, University of Wollongong, Australia, 1994.
- H. S. Andersson, J. G. Karlsson and S. A. Piletsky, J. Chromatogr. A, 1999, 848, 39–49 CrossRef CAS.
- D. Batra and K. J. Shea, Curr. Opin. Chem. Biol., 2003, 7, 434–442 CrossRef CAS.
- G. Sauerbrey, Z. Phys., 1959, 155, 206–222 CrossRef CAS.
- R. K. Roy, A Primer on the Taguchi Method, Society of Manufacturing Engineers, Van Nostrand Reinhold, New York 1990 Search PubMed.
- E. Naderi, G. Ghoreishy, M. H. R. Ghoreishy and G. R. Bakhshandeh, Iran. Polym. J., 2011, 20, 587–596 Search PubMed.
- S. Datta, G. Nandi and A. Bandyopadhyay, J. Manuf. Syst., 2009, 28, 55–63 CrossRef PubMed.
- A. K. Dubey and V. Yadava, Opt. Laser. Eng., 2008, 46, 124–132 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra00802b |
| This journal is © The Royal Society of Chemistry 2014 |


