Critical behaviour at the nematic–smectic A phase transition in a binary mixture showing induced nematic phase
Abstract
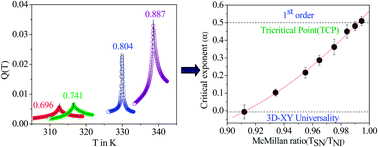
High resolution optical birefringence (Δn) measurements have been performed on thirteen mixtures of two smectogenic compounds, 5-trans-n-pentyl-2-(4-isothiocyanatophenyl)-1,3-dioxane (5DBT) and 4-cyano-4′-n-decyloxy-biphenyl (10OCB), showing an induced nematic phase from the optical transmission method for two different wavelengths. The values of the birefringence have also been compared with those determined from the thin prism method. The critical behaviour of the nematic–smectic A (N–SmA) phase transition has been studied from the birefringence measurements and the nature of the transition in these mixtures has been discussed. The critical exponent values for these mixtures show a definite pattern when plotted both against molar concentration as well as McMillan ratio (TSN/TNI). On both sides of the phase diagram, a uniform crossover trend from second order to first order N–SmA phase transition is observed as the tricritical point (TCP) is approached. For both the TCP's there exists a common value of the McMillan ratio = 0.992. In addition, the 3D-XY model is reached almost exactly at x5DBT = 0.696 for which the McMillan ratio is 0.912.

 Please wait while we load your content...
Please wait while we load your content...