Nucleation of decahedral Ag nanocrystals

Abstract

Via MD simulation, we show that the transition barrier between icosahedral (Ih) and decahedral (Dh) silver clusters increases strongly with cluster size and thus effectively prohibits thermally induced transformation. It is further shown that coalescence of preformed Ih clusters may indeed serve as an effective path for the nucleation of Dh-like multiply twinned nanoparticles.

---

Silver, Au, or Pd nanorods/nanowires possessing pentagonal cross-sections are known to result from anisotropic growth from decahedral (Dh) seeds or multiply twinned particles (MTPs) of a five-fold symmetry axis. The growth mechanism is believed to be the capping of high-energy (100) planes by surface-selective agents, such as in the synthesis of Ag nanorods or nanowires via the “polyol process” using poly(vinyl pyrrolidone) as the capping agent.^1–4 However, the kinetic path leading to the incipient formation of Dh MTPs with (100) facets remains unclear.^5,6 Theoretically predicted phase diagrams^7–10 generally suggest that the icosahedral (Ih) cluster is thermodynamically favored when the size is small; as the cluster size increases, the Dh form becomes preferred, but the Ih-to-Dh transformation appears prohibited presumably by a high free-energy barrier.^9,10 Via molecular dynamic simulation, Baletto et al.^5,6 demonstrated that the growth mechanism and the resulting structure of nanometer Ag clusters depend on kinetic factors and can differ from the minimum-energy structure. Via transmission electron microscopy (TEM), Koga et al.¹¹ made in situ observations on structural transformation of Au nanoparticles annealed in a helium heat bath. Results indicated that Au nanoparticles (6 to 14 nm in size) may undergo Ih → Dh transformation, but only at high temperatures (1150 to 1300 K) near cluster melting, implying that the structural transformation is ruled by a cluster size-dependent barrier. In other words, a nanoparticle can be easily trapped in its Ih form as a local minimum of the potential energy surface, from which it cannot escape at moderate temperatures due to the prohibitively high barrier. A few questions may then arise. Firstly, what is the origin of the prohibitively high transformation barrier between nanometer-sized Ih and Dh clusters? More practically, if the shape transformation is prohibited at moderate temperatures, what is the nucleation mechanism of Dh nanocrystals in the polyol process at temperatures typically <500 K?

To answer these questions, here we show via molecular mechanics (MM) and molecular dynamics (MD) computation over Ag clusters that the size-dependence in the relative stability of Ih and Dh clusters is mainly due to increased deviations from strict FCC packing in Ih clusters of increasing size.¹² We start with comparing the static energy and structures of various Ih and Dh clusters. This is followed by adding thermo-kinetic energy for MD simulation to examine details of the transformation process between Ih and Dh clusters. To mimic the kinetically restricted transient structures, we adopt a partial geometry-optimization (GO) procedure. Size-dependent transition barrier is then obtained via Eyring analysis¹³ of isothermal MD results. From the transitional structures, we show that transformation between Ih and Dh shapes involves cooperative in-plane rotation of atomic layers, leading to steadily increased barrier height with increasing cluster size. This observation effectively excludes nucleation of Dh nanocrystals via shell-by-shell embryonic growth. Furthermore, we show via MD simulation that an alternative route of coalescence^14–18 of Ih clusters may indeed give rise to Dh-shaped nuclei, in support of the “aggregative” mechanism proposed by Giersig et al.¹⁷ based on TEM observations of Ag clusters.

Relative cluster stability

Via full GO, we built Ih and Dh clusters with the number of shells (S) ranging from 2 to 20 (cf. Fig. S1 and S2 in the ESI†). Size-dependent characteristics of Dh and Ih clusters in the range of S = 2 to 20 are shown in Fig. 1. Generally, the total potential energy (E) increases strongly with increasing cluster size from S = 2 to 5, followed by more moderate and nearly linear increases for S ≥ 7. For small clusters, the Ih form is more stable than the Dh form, which may intuitively be attributed to the favorable low-energy (111) surfaces of Ih clusters. However, the limiting slope dE_Ih/dS = 0.040 eV for large Ih clusters is significantly greater than dE_Dh/dS = 0.025 eV of the corresponding Dh clusters, resulting in reversed stability for S > 17 (cf. inset in Fig. 1). [Here we consider only the Ino decahedra¹⁹ with the same atom numbers of their Ih counterparts; grooved along the high-energy twin edges, the Marks decahedra^8,20 are further stabilized and hence expected to result in a slightly lowered Dh curve of smaller slope and Ih–Dh crossover size.] The linearity in the high-S range signifies constant increase in potential energy with each added shell, indicating nearly constant contribution from each added surface shell in the case of Dh clusters. Due to the lower surface energy of (111) planes as compared to (110) or (100) planes, the surface energy contribution of an Ih cluster should presumably be weaker than that of its Dh counterpart; the higher value of dE_Ih/dS thus implies strong contributions from the interior of Ih clusters.

Fig. 1 MM-calculated variations of the static potential energy E of Ih and Dh clusters in the size range of S = 2 to 20. Also shown are the corresponding fraction of surface atoms (the same for Ih and Dh forms) and the energy difference (ΔE) between Ih and Dh clusters. For S ≤ 17 (at which the cluster is ca. 9 nm in diameter, with edge length of 4.7 nm), the Ih cluster is more stable than the Dh cluster; the tendency is reversed for S > 17.

Given in Fig. 2 are radial distribution functions (RDFs) for Ih and Dh clusters of S = 20. The RDF of the Dh cluster remains close to that of the ideal face-centered cubic (FCC) packing, although the peaks broaden slightly with increasing distance. In contrast, RDF peaks of the Ih cluster are clearly broadened and skewed to the left, indicating significant deviations from strict FCC packing in order to accommodate the 10 five-fold rotational symmetry axes.^20,21 This is also reflected in the slight convexity of the nominal (111) surfaces while the edges remain fairly straight, as shown by the expanded view (inset in Fig. 2) of one of the 20 constituting tetrahedral sectors of the Ih cluster.

Fig. 2 Comparison of static RDF profiles of Ag atoms in the bulk crystalline state with those in Ih and Dh clusters (S = 20, comprising N₂₀ = 24 739 atoms, ca. 10.6 nm in diameter). The RDF of the Dh cluster indicates only slight deviations in atomic packing from bulk crystals, whereas broadened RDF peaks of the Ih cluster indicates significant deviations. The inset demonstrates displaced atomic positions (as colored layers of connected dots), endowing convexity to the nominal (111) planes.

Dh–Ih transformation

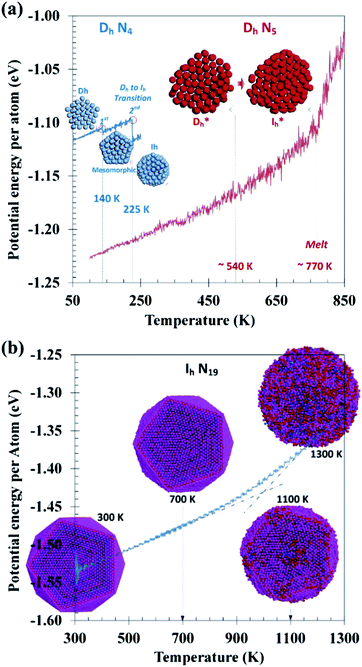
To demonstrate dynamic features of the thermally activated transformation between Dh and Ih shapes, thermodynamically unfavorable clusters were brought to high temperatures for MD observation. Given in Fig. 3a are potential energy evolution profiles of Dh clusters of S = 4 upon heating from 50 to 250 K and S = 5 from 100 to 1100 K. For the 4-shell cluster, there are two identifiable transitional steps, a minor one at 140 K and the major one at 225 K. As the former corresponds only to loosening and displacement of peripheral atoms of pentagonal cross-sections and involves only a slight decrease in energy, it is considered pre-transitional. The latter step corresponds to a main decrease in energy and involves coordinated twisting of the entire cross-sectional structure into Ih packing, as preliminarily shown by the inserted MD snapshots. These observations suggest T_Dh→Ih ≈ 225 K for the 4-shell cluster. As for the 5-shell cluster, no apparent discontinuities can be identified in the heating profile, implying a high Dh → Ih transition barrier. Without a step change in energy, there could be a certain structural change around 540 K, which would correspond to a continuous transition between “activated” structures (denoted as Dh* and Ih* in Fig. 3a), but strict Ih symmetry was never reached before melting of the cluster at ca. 770 K.

Fig. 3 (a) Potential energy evolution profiles of Dh clusters with S = 4 and 5 during heating from 50 to 250 K and 100 to 1100 K, respectively. For the 4-shell cluster, a minor transitional step at 140 K and a major step at 225 K can be observed. Changes in atomic packing before/after the transitional steps are shown by the accompanying snapshots. In the 5-shell case, no step-like features can be identified before melting of the cluster at ca. 770 K. With increasing temperature, thermally induced fluctuations gradually drive the cluster out of its Dh shape yet without reaching the Ih geometry. Structurally, a qualitative change occurs around 540 K, as shown by the corresponding snapshots (designated as “excited” Dh* and Ih* forms). (b) Potential energy evolution profile for a 19-shell Ih cluster during heating from 300 to 1300 K. In the selected snapshots, atoms originally on the surface are marked in pink for easy identification. The (111) facets and the Ih geometry remain intact below 700 K; surface melting can be observed around 1000 K, followed by complete melting into an isotropic droplet above 1100 K without passing through the Dh form.

Given in Fig. 3b is the potential energy evolution profile of an N₁₉ cluster of Ih symmetry during heating. Corresponding snapshots demonstrate that the characteristic (111) facets remain intact up to 700 K, followed by surface melting above 1000 K before final melting into an isotropic droplet near 1200 K without going through Dh symmetry. This observation again implies a high kinetic barrier for Ih → Dh transformation.

Transition barrier

In the framework of Eyring's transition-state theory,¹³ the rate of transformation may be expressed as k = (k_BT/h)exp(ΔS^‡/k_B)exp(−ΔH^‡/k_BT) in which k_B and h are respectively the Boltzmann and Planck constants whereas ΔS^‡ and ΔH^‡ the activation entropy and enthalpy. For the present MD simulation under the NVT ensemble, ΔH^‡ = ΔE^‡ whereas the transition rate k may be defined operationally as the reciprocal of the delay time τ between the pre-transitional (first) step and the major (second) step of the Dh → Ih transformation (cf. Fig. 3a). Via a series of isothermal MD runs over the 4-shell Dh cluster at temperatures ranging from 200 to 325 K (cf. insert of Fig. 4; τ values obtained from 3 MD runs at each temperature are list in Table S1, ESI†), 〈τ〉 is found to decrease with increasing temperature. With k ≡ 〈τ〉⁻¹, we have ln(k/T) = (−ΔE^‡/k_B) T⁻¹ + ln(k_B/h) + (ΔS^‡/k_B), which gives ΔE^‡ ≈ 0.22 eV and ΔS^‡ ≈ 2.7 × 10⁻⁴ eV K⁻¹ from the Eyring plot given in Fig. 4. The positive value of ΔS^‡ indicates decreased order of cluster during transformation.

Fig. 4 Eyring plot for Dh → Ih transformation of the 4-shell cluster in the temperature range of 200 to 325 K. The inset demonstrates the delay time τ between the first pre-transitional step and the occurrence of the major Dh → Ih transition at 200, 225 and 250 K. The slope and intercept of the Eyring plot yield ΔH^‡ = ΔE^‡ ≈ 0.22 eV and ΔS^‡ ≈ 2.7 × 10⁻⁴ eV K⁻¹.

Transitional structures

Results of MD simulation provide transient structures, albeit mixed with thermal fluctuations. To eliminate effects from thermal perturbations, a scheme of partial GO was adopted for each MD frame (in 10 fs recording period) using the steepest-descent method for 100 differential steps to take advantage of its quick-approaching but slow-converging characteristics. Given in Fig. 5 is the transient potential energy evolution profile (relative to the potential energy of the final Ih structure) of the 4-shell cluster at 300 K. There is an immediate transitional step at a short MD time of t_MD = 0.5 ps with a barrier of 0.20 eV and a minor energy drop (0.20 eV), followed by a plateau period of t_MD = 0.6 to 30 ps which corresponds to a metastable structure with peripheral atoms of the cross-sectional R layer (cf. inserts in Fig. 5) slightly rotated with respect to the principal axis. This is followed by a second transitional step at t_MD ≈ 35.6 ps, again with a minor energy drop (by 0.40 eV) and a barrier of 0.25 eV, which is comparable to the value of ΔE^‡ ≈ 0.22 eV determined from the Eyring analysis. The corresponding structural change involves the coordinated rotation of the double-deck C/B layers (cf. also Fig. S5 in ESI† for layer-by-layer views). Subsequently, there are moderate fluctuations (±0.1 eV) for t_MD = 36 to 50 ps, with rotational adjustment of peripheral atoms of the G layer. Finally, upon passing of a low barrier of ca. 0.15 eV for a significant energy drop of 2.8 eV at t_MD = 55 ps, the structural change to Ih symmetry is completed via cooperative adjustment of positions of nearly all atoms between the two pentagonal pyramids. To summarize, the Dh → Ih transformation involves firstly the sliding of a ring of peripheral atoms with respect to interior atoms (with moderate friction) of the R layer. The loosened surface restriction allows for coordinated rotation of atoms in the double-deck (C/B) layers connecting to the base of the end pyramid (with high friction except for the peripheral atoms), and finally the fine adjustments of atomic positions (with low friction) of the entire stem between the end pyramids to reach Ih symmetry for the major decrease in potential energy.

Fig. 5 Relative total potential energy evolution profile along the partially geometry-optimized MD trajectory of the 4-shell cluster at 300 K. Partial GO was made to each MD frame (in 10 fs intervals) with the steepest-descent method for 100 steps. This effectively eliminates noises from thermal fluctuations for representative transient structures given as inserts. Atoms in the Dh cluster are colored as red (R), yellow (Y), green (G), cyan (C), and blue (B) according to their initial positions to allow for easy tracking of the atomistic process. The first transitional step at t_MD = 0.5 ps with a barrier of ca. 0.20 eV corresponds to displacements of peripheral atoms in the cross-sectional R layer. The second step with a barrier of ca. 0.25 eV corresponds to the coordinated rotation of atoms in C and B layers where the peripheral atoms experience negligible fraction. The final step with a barrier of ca. 0.15 eV corresponds to cooperative yet fine adjustment of atomic positions to reach Ih symmetry for a major energy drop.

Size-dependence

As ΔE^‡ is dominated by the high-friction rotation step, we may now address its size dependence with the assumption that the same atomistic mechanism applies to clusters of different sizes. This rotation step involves friction experienced by interior atoms of a neighboring double-deck C/B pair (cf. Fig. 5 and S5†) except the central atom of the C layer that remains little displaced, the number of which may be denoted as X_S. We assume each of the X_S atoms contribute equally to the barrier upon start of rotation. For the 4-shell cluster, the transformation barrier is ca. 0.24 eV with X₄ = 15 (cf. Fig. S5†), yielding 0.016 eV per atom. For the 3-shell cluster, we have X₃ = 5 and hence ΔE^‡ = 5 × 0.016 = 0.08 eV, in good agreement with the value obtained from the corresponding MD simulation (shown in Fig. S6, ESI†). In the case of 5-shell cluster, we have X₅ = 30 and hence ΔE^‡ = 0.48 eV, which explains the absence of Dh → Ih transformation in a single MD run (Fig. 2a). Because X_S increases fairly quickly with S, e.g., X₆ = 50, X₇ = 75, and X₁₂ = 275, we have correspondingly increased ΔE^‡ to 0.8, 1.2, and 4.4 eV with increasing cluster size.

As we are not aware of any report on Dh → Ih transformation of Ag clusters, the TEM study of Koga et al.¹¹ on stability of Au clusters (prepared from condensation of Au vapor with a carrier stream of helium) may serve the purpose of a crude comparison. Firstly, they observed that as-grown Au clusters were mainly of Ih form, consistent with a shell-by-shell growth mechanism.²² After annealing at T_a = 1223 K, clusters with diameter d < 14 nm became dominantly in the Dh form, indicating thermally activated Ih → Dh transition up to S ≈ 25, consistent with the notion of increased barrier height with increasing cluster size. Notably, for smaller clusters of d < 6 nm, the population of Ih clusters was ca. 40%, quite respectable compared to near absence of Ih clusters in the range of 6 nm < d < 14 nm. As this T_a is within the melting range of small Ih clusters, kinetic effects from recrystallization of isotropic melt droplets during uncontrolled cooling after annealing are highly likely. With due consideration of the kinetic effects, we may take the fairly high Ih population for d < 6 nm as hints of thermodynamic preference of small Ih clusters. As their observations for lower (1175 K) or higher T_a (1273 K) cases appear to be strongly affected by the kinetic effects, we choose not to discuss further on these. It suffices to state that all their results are consistent with the picture of reversed stability and increased transition barrier with increasing cluster size if kinetic effects are duly considered.

Coalescence

As a final point, we remark on the formation of Dh-like MTP nuclei with (100) surfaces in the polyol solution process. According to Fig. 1, the Ih form is thermodynamically preferred for small clusters. One would therefore expect Ih clusters as nuclei for subsequent growth of nanocrystals. As the Ih cluster grows beyond S = 17, it becomes thermodynamically unfavorable but the transition barrier for Ih → Dh transformation increases strongly with cluster size to be prohibitively high. This effectively excludes development of Dh nuclei from straightforward shell-by-shell growth^5,6,22 of single-cluster embryos in the moderate temperature range (<500 K) adopted for the polyol solution process. As an alternative, we consider the “aggregative” mechanism^14–18 in terms of coalescence of clusters. This mechanism is intuitively plausible for the discussion of Ih–Dh transformation in view of the immediate anisotropy upon contact of two nearly spherical Ih clusters. Fig. 6 demonstrates such a coalescence process for two Ih clusters of S = 4 to form an anisotropic cluster with exposed (100) and (111) surfaces. Atoms of the final (100) surfaces are from different parts of the two Ih clusters, signifying extensive rearrangement of atomic positions. To allow for coalescence, a high concentration of Ih clusters is needed; this is certainly satisfied in the typical polyol process.

Fig. 6 Potential energy evolution profile and selected MD snapshots during coalescence of two 4-shell Ih clusters at 420 K. The blue line indicates the original potential profile whereas the red line the smoothed profile by averaging over the neighboring 50 steps. Initially, the two clusters (colored generally in blue and pink, respectively, but with atoms in the (100) surface of the final frame marked in yellow) were set apart by 20 Å center-to-center. The intermediate snapshots demonstrate the emergence of a primitive (100) surface at t_MD ≈ 20 ps upon merging of clusters; subsequent reorganization resulted in energy-stabilized packing of interior atoms at t_MD ≈ 0.2 ns, followed by surface restructuring to achieve the anisotropic Dh-liked shape with well-defined (100) facets at t_MD ≈ 1 ns (shown in both side- and top-views).

Although mixed morphology intermediate to Ih and Dh forms for open-shell clusters were observed in the quenched structures of the MD study by Angulo and Noguez,²⁶ clear transformation in shape was not identified. In fact, Fig. 6 serves as an example for open-shell Dh-like clusters, where a highly anisotropic initial state is the key reason why the coalescence mechanism can be effective. For the single-cluster case, this highly anisotropic state is statistically disfavored within limited MD time scales. We note further that, although complex mechanisms of cluster growth generally disfavoring the formation of Dh clusters were indicated in earlier MD simulation studies of Baletto et al.,^5,6 Dh-like clusters were still occasionally observed. This also lends support to the idea that coalescence is playing a role in the formation of Dh nuclei, especially in the case of high cluster populations. From a formulism point of view, a careful reader may have noticed that only the total potential energy is adopted for discussion, respective contributions from static structural parameters such as vertices, edges, and facets^10,24 are not specifically addressed. However, the focus of the present work lies in dynamic evolution of cluster shape and the relevant transient structures that cannot be properly described using static, fully geometry-optimized structural parameters. It should also be noted that the present results correspond to clusters in vacuum to save computation efforts. The matrix (chemical environment) effect involved in the “polyol process” using poly(vinyl pyrrolidone) as the capping agent is not considered in the nucleation stage where isotropic Ih clusters are favored. One would certainly expect that the matrix effect may play a dominant role for the stabilization and subsequent growth of coalescence-induced Dh clusters, which is the subject of our on-going study.

System and method

Via geometry optimization, we built Ih and Dh clusters with the number of shells ranging from S = 2 to 20 and the number of constituting atoms N_S = 13 to 24 739 according to the “magic number rule” that N_S = 10S³/3 − 5S² + 11S/3 − 1.²¹ As our main interest was in the transformation between Ih and Dh shapes, we considered only the Ino-type²⁰ Dh clusters with m = n = S where m and n are atom numbers along the (100) facet edges perpendicular and parallel to the five-fold symmetry axis, respectively. Fully geometry-optimized Dh clusters of N₄ and N₅ atoms were chosen for phase transformation simulations using Accelrys® Materials Studio equipped with MD engine Forcite. To allow for planned extension to capping agent/Ag cluster interactions, the COMPASS forcefield (Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies)²³ with pair-wise potentials was used instead of the more elaborated many-body potentials.^24,25 Results of test calculations using COMPASS to estimate the diffusion barrier of an Ag adatom on the (100) surface led to a moderately underestimated value of 0.28 eV, three quarters of the experimental value (0.38 eV),²⁷ implying underestimated interactions among Ag atoms. Thus, the Dh–Ih transition barrier should be higher than the values reported here, but this does not affect our qualitative conclusion.

For general observations of transformation behavior and preliminary estimation of the Dh–Ih transformation temperature (T_Dh–Ih), “heating” MD runs were made for clusters of S = 4, 5, and 19, respectively, with the heating rate set at 10⁻¹ to 10⁻³ K ps⁻¹. With T_{Dh → Ih} estimated as ca. 225 K, a Dh cluster of S = 4 was chosen for isothermal MD simulation in the temperature range of 200 to 325 K to monitor detailed dynamics of the transformation process. In addition, MD simulation at 300 K was repeated with shorter time steps of 0.1 fs to identify the trajectory of structural evolution. Each MD frame in the trajectory was then partially energy-minimized (100 iterations using the quickly approaching but slowly converging steepest-descent method) to approximate the “kinetically accessible” transient structures. To simulate the coalescence process, two Ih clusters of S = 4 were set at an initial center-to-center separation of 20 Å at 420 K, followed by MD computation under NVT ensemble and COMPASS forcefield, with a cut-off distance of 1.25 nm and simulation time steps of initially 1 fs but later on 0.1 fs for better resolution during the coalescence stage. Additional details may be found in the ESI.†

Acknowledgements

This work is supported by both the Industrial Technology Research Institute and National Tsing Hua University. Thanks are due to the National Center for High-performance Computing (NCHC) for computer time and facilities and Professor Hsiao-Ching Yang of Catholic Fu-Jen University for constructive comments.

Notes and references

1. N. Wang, Y. Cai and R. Q. Zhang, Mater. Sci. Eng., R, 2008, 60, 1–51.
2. Y. Xia, Y. Xiong, B. Lim and S. E. Skrabalak, Angew. Chem., Int. Ed., 2009, 48, 60–103.
3. A. R. Tao, S. Habas and P. Yang, Small, 2008, 4, 310–325.
4. Y. G. Sun, B. Mayers, T. Herricks and Y. N. Xia, Nano Lett., 2003, 3, 955–960.
5. F. Baletto, C. Mottet and R. Ferrando, Phys. Rev. Lett., 2000, 84, 5544–5547.
6. F. Baletto, C. Mottet and R. Ferrando, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155408.
7. A. L. González, C. Noguez and A. S. Barnard, J. Phys. Chem. C, 2012, 116, 14170–14175.
8. S. Patala, L. D. Marks and M. O. de la Cruz, J. Phys. Chem. Lett., 2013, 4, 3089–3094.
9. J. P. K. Doye and F. Calvo, Phys. Rev. Lett., 2001, 86, 3570–3573.
10. F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371–423.
11. K. Koga, T. Ikeshoji and K. Sugawara, Phys. Rev. Lett., 2004, 92, 115507.
12. A. L. Mackay, Acta Crystallogr., 1962, 15, 916–918.
13. H. Eyring, Chem. Rev., 1935, 17, 65–77.
14. J. J. Métois, M. Gauch, A. Masson and R. Kern, Surf. Sci., 1971, 27, 463–482.
15. P. Shen, Y. Y. Fahn and A. C. Su, Nano Lett., 2001, 1(6), 299–303.
16. R. L. Penn, J. Phys. Chem. B, 2004, 108, 12707–12712.
17. M. Giersig, I. Pastoriza-Santos and L. M. Liz-Marzan, J. Mater. Chem., 2004, 14, 607–610.
18. J. Zhang, F. Huang and Z. Lin, Nanoscale, 2010, 2, 18–34.
19. S. Ino, J. Phys. Soc. Jpn., 1969, 27, 941–953.
20. L. D. Marks, Philos. Mag. A, 1984, 49, 81–93.
21. J. P. K. Doye and D. J. Wales, Chem. Phys. Lett., 1995, 247, 339–347.
22. K. Koga and K. Sugawara, Surf. Sci., 2003, 529, 23–35.
23. (a) H. Sun, Macromolecules, 1995, 28, 701–712; (b) H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364; (c) H. Sun, P. Ren and J. R. Fried, Comput. Theor. Polym. Sci., 1998, 8, 229–246.
24. A. S. Barnard, Rep. Prog. Phys., 2010, 73, 086502.
25. F. Montalenti and R. Ferrando, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 5881–5891.
26. A. M. Angulo and C. Noguez, J. Phys. Chem. A, 2008, 112, 5834–5838.
27. L. Bardotti, M. C. Bartelt, C. J. Jenks, C. R. Stoldt, J.-M. Wen, C.-M. Zhang, P. A. Thiel and J. W. Evans, Langmuir, 1998, 14, 1487–1492.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra00186a

---